基于矩阵特征体系的一级可逆反应动力系统结构分析

左 路， 胡 玮， 钟欣欣

(湖北大学化学化工学院，武汉 430062)

1 引 言

化学动力学的重要目的就是探索反应过程中不同反应物质量的关联，描述其浓度变化的演变规律，并预测反应系统宏观行为.反应物质量的关联及演变规律由反应速率微分方程描述[1-2]，微分方程组的建立则依赖于化学动力学参数——反应速率常数.根据是否已知速率常数，化学反应动力学研究通常呈现两种互逆的研究路径：已知速率常数时，考虑给定的反应初始态，由解轨迹描述并预测反应系统的宏观行为；未知速率常数时，研究侧重于如何由实验路径估计动力学信息.实际中研究者常面对后一种情形，因此估计反应速率常数成为反应化学动力学研究的首要任务.但是估计方法需要面对若干困难，诸如如何进行有效的实验并获得精确的实验路径，以及当反应系统复杂度增加时，如何利用有限的实验路径估计所有的反应速率常数.前述情形在催化与酶化学中很常见，此时的反应体系通常为高耦合复杂系统，因此造成高维度背景下化学动力学研究异常困难.

1962年，文献[3]建立了复杂体系结构性分析的基本方法，利用速率方程组系数矩阵的代数特性构建估计速率常数的计算方法，从而开辟了利用矩阵方法研究化学动力系统的新途径.基于Wei和Prater结构方法，文献[2]建立了反应速率常数的正交估计法.本文将深入分析一级可逆反应体系速率方程组，不仅证明了速率常数矩阵特征系统的固有性质，也揭示出这些性质如何构建得到反应体系的结构系统.

2 速率常数矩阵特征体系性质

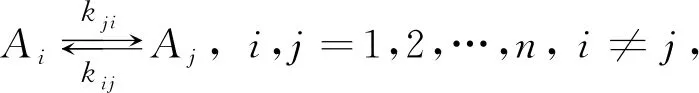
dx(t)/dt=Kx(t)，

其中系数矩阵K由速率常数构成

dx(t)/dt=Kx(t)中每个微分方程形如

上式右端函数受控于t时刻所有物质的量，即时刻t处物质Ai的反应速率dxi(t)/dt受到所有与Ai相关的反应通道影响.xi项的系数则对应于所有由物质Ai反应的通道.由于反应物质的量必为非负值，时刻t处各物质的摩尔分率必须满足

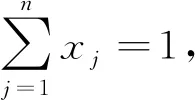
(1)

深入分析速率常数矩阵K的特征体系，不仅揭示出K的结构性质有助于建立文献[2]中的正交估计法，同时揭示了一级可逆反应体系的结构化特征.

2.1 速率常数矩阵K有唯一零特征值

观察速率常数矩阵可知K的每列元素和为零，则K为奇异方阵，必有零特征值.但是仅由K的行列式值无法直接判断零特征值的代数重数.记K的特征多项式为

p(λ)=λn+c1λn-1+c2λn-2+…+cn-2λ2+cn-1λ+cn，

其中系数ck=(-1)kSk,Sk为K的所有k阶主子式的和.由于K为奇异方阵，则系数cn=0，特征多项式可以变化为

p(λ)=λ(λn-1+c1λn-2+c2λn-3+…+cn-2λ+cn-1).

若系数cn-1≠0，则特征方程p(λ)=0仅有唯一零根.

考虑K的取自i1,i2,…,in-1行、列的n-1阶主子式

对于一级可逆反应网络而言，速率常数矩阵K的零元素必在对称位置出现，即若某个kij=0，则必有逆向反应的速率常数kji=0.并且K的每一行、列元素必不全为零，否则零行、列对应的物质将不在反应系统中存在.因此K的任一n-1阶主子式对应的矩阵K(n-1)至少有一列满足严格对角占优且不可约，则K的所有n-1阶主子式值非零[4].但是仅由此点性质无法判断所有n-1阶主子式值的和为非零值.

令k=n-1，主子式|K(k)|的展开式中必有一项为主对角线上k个元素的乘积，即为

(3)

化简得到

此项展开式中至少有一个乘积项kj1i1kj2i2…kjn-1in-1不为零，否则|K(k)|的所有元素必为0.并且当k为奇数时，(3)式值小于零，否则(3)式值将大于零.

|K(k)|展开式中的其他项最多含有k-2个主对角元素，考虑展开式中包含k-2个主对角元素的项，则此项乘积因子中某两个位置的元素取自非对角元素，形如

(4)

可见(4)式与(3)式符号一致.考虑展开式中包含k-3个主对角元素的项，形如

(5)

此项与(4)式符号相反.形如(5)式的每一项均包含在(4)式形式中，仅仅符号相反.因此符合(5)式结构的项均在形如(4)式的项中抵消掉.依此类推，从k-3开始每一个包含k-(2j+1)个主对角元的项必包含于含k-2j个主对角元的展开项中，且由于符号相反得以抵消.|K(k)|最终值为k个主对角元的乘积项、k-2j个主对角元乘积项的抵消剩余项，以及不含主对角元的乘积项这三部分之和.对于k阶主子式而言，前述每一项均符号相同，则K的每一个k阶主子式非零.因此任意n-1阶主子式|K(n-1)|非零且符号相同，使得所有n-1阶主子式和Sn-1非零，从而系数cn-1≠0，因此特征方程p(λ)=0仅有1个零根.

2.2 零特征值对应的特征向量构成系统平衡状态向量

由统计热力学中的精细平衡原则[5-7](the principle of detailed balance)可知，可逆反应系统经历一定反应时间后将达到唯一平衡态.实际上，速率常数矩阵的构成就已经充分保证了一级可逆反应体系唯一平衡态的存在，且此平衡态构成对应于速率常数矩阵零特征值的特征向量.

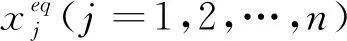
dx(t)/dt=Kx(t)

在t→+∞时满足dxeq/dt=Kxeq=0，即K的零特征值(记为λ1=0)对应于平衡态向量.由于零特征值的代数重数为1且几何重数亦为1，则K的零特征值对应的全部特征向量都在n中的一条直线上.但是分量值均为正且分量和为1的特征向量仅有一个(记为v1)，并满足dv1/dt=Kv1=0.此时反应体系达到平衡态xeq(xeq=v1)，即v1为满足反应系统约束的对应于零特征值唯一特征向量.

2.3 K的所有特征值均小于或等于零

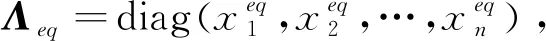
Γ的所有特征值全为实数且小于或等于零[2](记为-λj,j=1,2,…,n).由相似关系不变性，-λ1,-λ2,…,-λn同时也是K的特征值.

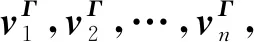
满足Γ=PΛP-1，其中对角矩阵Λ=diag(-λ1,-λ2,…,-λn)，那么有

若记

则得到K=VΛV-1，因此v1,v2,…,vn为K对应于-λ1,-λ2,…,-λn的特征向量.

2.4 非零特征值对应的特征向量的分量和必为0

令特征向量vj=(v1j,v2j,…,vnj)T,j=1,2,…,n，由于Kvj=-λjvj，则非零特征值-λj,j=2,3,…,n对应的特征向量的分量和应满足

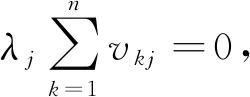
3 速率常数矩阵特征体系与动力学参数估计

3.1 反应轨迹结构

利用K=VΛV-1解耦反应体系dx(t)/dt=Kx(t)得到微分方程dy(t)/dt=Λy(t)，解轨迹x(t)则变换为虚拟解轨迹

y(t)=V-1x(t)=(y1(t),y2(t),…,yn(t))T.

解耦后的每个微分方程形如dyj(t)/dt=-λjyj(t)，此时的反应组分yj(t)(以下称为虚拟组分)并非真实反应物摩尔组分数，因此不必受到(1)式约束.求解微分方程dy(t)/dt=Λy(t)将得到虚拟解轨迹y(t)=eΛty(0)，其中矩阵指数函数eΛt=diag(e-λ1t,e-λ2t,…,e-λnt),y(0)=V-1x(0)为反应初始态x(0)对应的初始虚拟组分态.将虚拟解轨迹y(t)还原得到原始反应体系dx(t)/dt=Kx(t)的解轨迹

x(t)=VeΛtV-1x(0)=c1v1+c2e-λ2tv2+…+cne-λntvn，

(6)

其中系数c1,c2,…,cn即为虚拟初始状态y(0)的所有分量值.当反应体系的速率常数kij未知时，利用(6)式可以估计矩阵K的特征值与特征向量.

由于v1,v2,…,vn线性无关可以构成n的基，因此初始态向量表示为

x(0)=c1v1+c2v2+…+cnvn.

而状态向量x(0)与平衡态向量v1必须满足约束(1)式，且非零特征值的特征向量分量和为0，则上式右端向量的分量和应为1，即

得到系数c1=1.因此(6)式化简为

x(t)=v1+c2e-λ2tv2+…+cne-λntvn.

(7)

当反应时间t→+∞时，较大绝对值的非零特征值-λj使得cje-λjtvj快速趋于零向量，而具有最小绝对值的非零特征值对应的特征向量将决定x(t)沿什么路径趋于平衡态.

3.2 特征直线反应路径

实验反应路径通常选择从最简单的初始组分开始，即从反应空间的某个顶点对应的纯物质初始态进行反应，并测得反应轨迹与平衡态v1.反应轨迹趋近平衡态时的切线就是|-λj|min(-λj≠0)对应的特征向量vj所在直线，直线拟合平衡态附近的反应轨迹，并求得拟合直线与反应空间边界的交点，即为沿特征向量vj所在直线的反应进程初始点(记为xvj(0)).此初始点对应于(7)式的系数分别为1,0,…,0,cj,0,…,0，使得(7)式简化为特征直线反应路径xvj(t)=v1+cje-λjtvj.由于xvj(0)=v1+cjvj，为了方便将重新放缩后的特征向量cjvj作为与特征值-λj对应的特征向量，仍记为vj.由xvj(0)-v1从而求得特征向量vj.

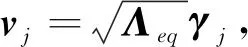
K=Vdiag(-λ1,-λ2,…,-λn)V-1.

4 结 论

对于一个n组分的一级可逆复杂反应网络而言，速率常数矩阵至少包含2(n-1)个动力学参数，至多包含n(n-1)个.随着组分数n的增加，系统复杂度与待估计参数个数急速增加.如何利用有限的实验反应路径估计动力学参数并描述反应体系的宏观行为便成为动力学研究的困难之处.深入分析速率常数矩阵的结构特征，不仅建立了基于矩阵特征体系的反应模型及反应轨迹结构性描述，还提供了利用少量纯物质反应初始态的实验路径估计动力学参数的方法.与此同时，基于矩阵特征体系的反应轨迹几何视角描述，为进一步优化实验路径、寻找最短实验路径指明了研究方向.

致谢作者衷心感谢审稿专家提出的宝贵意见，以及相关文献对本文的启发与激励.