对称形式的q-mKP系列的流方程

陆苏鹏， 田可雷

(合肥工业大学数学学院，合肥 230601)

1 引 言

Kadomtsev-Petviashvili系列[1]和Davey-Stewartson系列[2]一直是可积系统领域的热门研究方向之一.通过对Lax算子以及Lax方程做一些改变，可以得到KP系列的推广情形，如mKP系列、q-KP系列、q-mKP系列、离散KP系列、无色散KP系列等[3-8].对称形式的q-mKP系列是将微分算子改成对称形式的q-微分算子得到的[9].想要研究其可积性质，须先讨论其流方程.本文主要内容是给出对称形式的q-mKP系列流方程的等价形式.

2 对称形式的q-mKP系列

定义1对称形式的q-微分算子∂qq-1定义为[10]

定义2移动算子定义为

θif(x)=f(ix),i=q或q-1.

注意这里的移动算子θi与对称形式的q-微分算子∂qq-1不能交换.实际上它们有如下的关系

对称形式的q-微分算子∂qq-1满足莱布尼茨规则

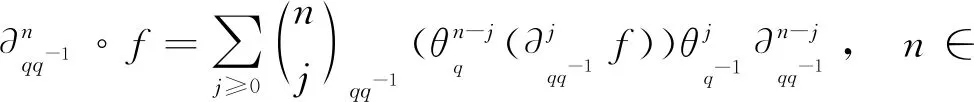
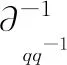
给出几个具体的公式

∂qq-1∘f=(θqf)∂qq-1+(∂qq-1f)θq-1,

定义3对称形式的q-mKP系列的Lax方程定义为

Ltm=[(Lm)≥1,L],m=1,2,3,…,

(1)

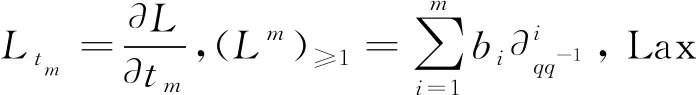
(2)

3 对称形式的q-mKP系列的流方程

为了简便，把式(2)写成形式

(3)

并引入记号

通过计算，pj(n)和qj(n)满足如下关系

(4)

注意从式(8)中发现pj(n)可以由ui唯一确定，即

pj(n)=fjn(u0,u1,u2,…,un-j),n=1,2,3,…,

(5)

其中fjn是∂qq-1关于{u0,u1,u2,…,un-j}的微分多项式.

定理1对称形式的q-mKP系列的流方程表示为

(6)

其中

(7)

(8)

证由式(7)可知

从而有

Ltm=[(Lm)≥1,L]=[L-(Lm)<1,L]=[L,(Lm)<1]

其中i=r+α,j=i+h.再结合等式

即可完成证明.

定义4对n=1,2,3,…，对称形式的q-mKP系列的n-约化条件定义为Ln=(Ln)≥1.

上述n-约化条件等价为对于所有的j<1,有pj(n)=0.这意味着此时，只有前n个动态坐标(u0，u1，…，un-1)是独立的，且其他所有的高阶坐标uj都可以表示成关于(u0,u1,…,un-1)的微分多项式.由参考文献[7]，易得到以下定理.

定理2在n-约化条件下，对称形式的q-mKP系列流方程的等价形式表示为

U(n)tm=B(n)P(n,m),

(9)

其中

4 结 论

通过Lax方程计算对称形式的q-mKP系列的流方程，进一步给出在n-约化条件下流方程的等价形式，将无穷维流方程改写为有限维矩阵的形式，这为后续研究递归算子等其他可积性质提供基础.

致谢作者非常感谢相关文献对本文的启发以及审稿专家提出的宝贵意见.