焊缝检测实验与结果分析

林浩然，杨孟杰＊，梁士谦，侯毅恒

（桂林电子科技大学 机电工程学院，广西 桂林 541000）

0 引言

作为制造强国的中国，其无论在日常民用、国防建设，还是在基层建设等方面，都在广泛地使用焊接加工工艺。焊接过程中难以避免的产生的焊缝及其热影响区都是最容易产生裂纹的部位，也因此，与每个人的日常生活息息相关[1]。

我国对焊缝的检测研究很早便开始了，先后经历了无损探伤（Non-destructive Inspecting，NDI）、无损检测（Non-destructive Testing，NDT）和无损评价（Nondestructive Evaluation，NDE）三个阶段[2]。现如今，无损检测技术已经可以通过得到的信息对试件做出定量的评价。

在对焊缝使用无损检测方面，Legender[4]提出并实现了用Lamb 波对焊缝裂纹进行自动分类检测。Y.Cho[3]利用数值分析法，对在焊缝及其周边的Lamb 波模态转换问题进行了研究和分析。Sylvie 随后，孙斐然等[5]在近些年基于洛伦兹力机理的电磁超声换能器的数学建模的研究成果，得出了完整的耦合方程和建模过程，分析了偏置磁场、激励线圈等参数对换能效率的影响。接着，N.JULURI 等[6]基于特征导波理论，利用有限元思想建立焊缝模型，通过激励不同模态的Lamb 波，并成功证明出焊缝导波的存在。随后，Terrien N[7].建立出三维有限元仿真模型，探讨分析裂纹对焊缝导波的影响过程，对回波能量衰减与频散现象进行了分析。

将基于电磁超声技术，对焊缝进行无损检测仿真与实验，通过仿真软件完成能够激发单一模态的焊缝检测EMAT 模型的设计。通过得到电磁场和声场的主要特征，在声场中选取Lamb 波的A0 模态作为主导模式，分析裂纹对导波的响应特性，完成对焊缝细微裂纹的检测和判断，为基于电磁超声的焊缝检测进入工业普及应用打下基础。

1 Lamb 波的有限元模型

模型选用圆柱形磁体环境作为非均匀静态偏置磁场，选用A0 模态为主模式，磁体提离与线圈提离距离为0.25 mm；选用试件为500 mm × 500 mm × 3 mm的铝板；选用激励电流为汉宁窗调谐的五幅波[8]，激励频率为250 kHz，如图1 所示。

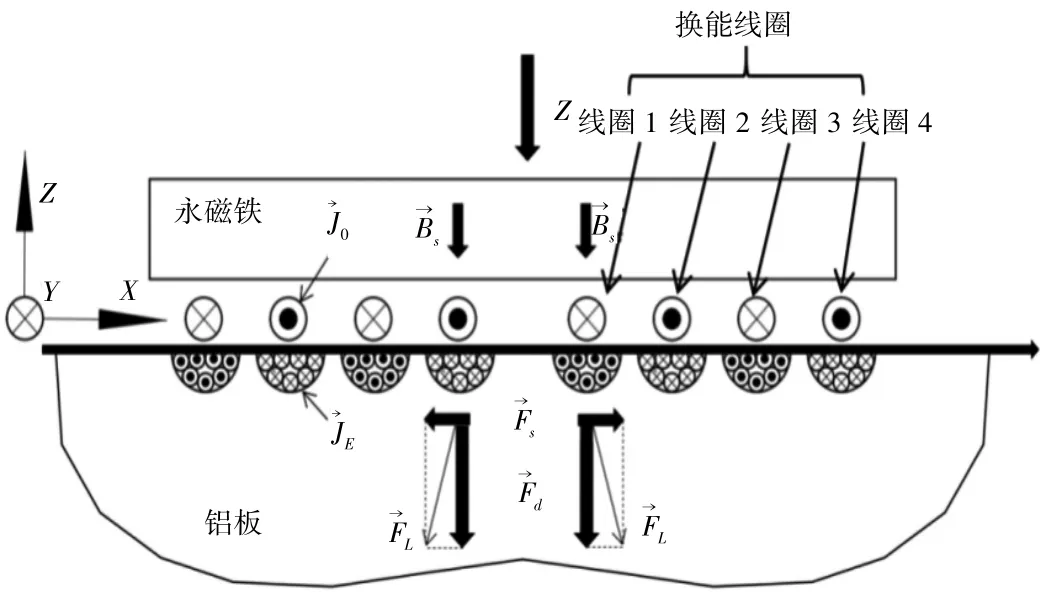
图1 基于洛伦兹力的EMAT 模型

搭建空气域几何模型时应考虑：（1）保证磁场作用范围以及超声波在铝材中的传播过程不受空气域的影响；（2）确保偏置磁场的静态磁场分布，保证偏置磁场作用范围的收敛性，故空气域尺寸设定为1000 mm × 50 mm。

换能线圈为标准PCB 制下四层螺旋线圈，横截截面为2 mm × 0.035 mm，相对位置满足式（1）。线圈匝数比依据四线圈调谐原则，通过设计变量法求得匝数比满足n1:n2:n3:n4= 3 : 6 : 9 : 10。

网格剖分直接决定了仿真模型的计算精度和工作量[9]，因此，本研究电磁耦合区域采用自由三角形网格剖分，在250 kHz 的激励频率下，趋肤层深度约为1 mm，因此限定铝板中的最大剖分网格为0.5 mm，偏置磁场与试件之间的剖分网格最大为0.8 mm。其余部分采用自由三角形过渡网格剖分即可，总体最大单元增长率设定为1.3，最小单元网格为0.1 mm。

具体的二维模型参数见表1。

表1 EMAT 模型参数

2 焊缝裂纹位置、尺寸的仿真分析

在Lamb 波与裂纹相互作用的声场分布中，发生最明显的就是电磁超声波的反射与衍射现象。其中，无论反射现象产生的回波，还是衍射现象产生的透射波，都包含了裂纹的全部信息。由于焊缝中的裂纹多为微小裂纹，因此将回波作为主要分析对象。

2.1 裂纹长度对回波的影响

相比于传统体波，Lamb 波具有自身独特的频散性，其与裂纹相互作用的机理并不同于传统的体波[10]。所以，裂纹长度与回波的相位、幅值等特征信息间一定不具有明显的关系。因此，本实验必须采用控制变量法，将除裂纹长度以外的其他参数设定为固定值，裂纹长度作为自变量，研究不同值的裂纹长度对回波的影响。仿真实验具体参数见表2。

表2 裂纹长度-裂纹参数

将裂纹长度D= range（60，10，170）进行仿真，对EMAT 接收端的回波进行捕捉，得到裂纹长度D与回波的幅值关系如图2 所示。

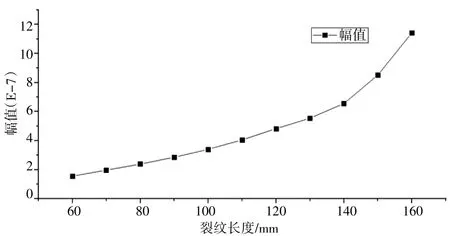
图2 裂纹长度与回波的幅值关系图

从图2 可知，总体上回波的幅值随着裂纹长度D的增大而增大。当裂纹长度D< 140 mm 时，回波的幅值增长速率相对恒定；当裂纹长度D＞140 mm 时，易知回波的幅值增长速率随着D的增大而增大。这是因为裂纹长度D越小，声场中Lamb 波对裂纹的衍射现象越明显，客观体现在裂纹周围传播介质频厚积的变化；当裂纹长度D越大，频厚积变化速率越大，发生Lamb 越过裂纹的衍射现象越困难，故回波的幅值增长速率也越大。所以当W< 140 mm 时，回波的幅值变化可以用于裂纹成像处理，当W＞140 mm 时，两者的线性关系变差，不再适合裂纹成像，但仍可以用于判断是否存在裂纹。

2.2 裂纹位置对回波的影响

由于焊缝特征导波的能陷效应，特征导波只沿着焊缝传播[11]。当与裂纹作用时，既不会发生能量泄露到母材，也不会发生模态变化，因此，当特征导波的在裂纹中传播时，相速度不变。因此，可以通过时域里回波的到达时间来判断裂纹距离。实验其他参数如下：

表3 裂纹位置-裂纹参数

为了保证波形清晰，保证激励波无法与反射波叠加在一起，裂纹与EMAT 的激励、接收探头的距离必须满足X= range（100，10，200）。此时得到裂纹位置X与回波到达EMAT 的时间关系如图3 所示。

图3 裂纹位置与回波到达时间关系图

从图3 上可以很直观地看出：在一定范围内，裂纹位置X与回波的到达时间成正比。将框中的各点到达时间转换为裂纹位置，可知：该范围的区间为五幅波总长。由此得出结论：在激励起始波的总长内，裂纹位置X随着回波的到达时间的增大而增大，且每段总长间成等差关系，差值为Lamb 波波长λ。所以，可以通过回波的到达时间来定量判断裂纹位置。

3 焊缝检测实验结果与分析

根据上述仿真分析，选用一发一收的方式进行实验研究。实验铝板为800 mm × 300 mm × 3 mm；裂纹尺寸为0.2 mm，位置为200 mm；激发频率为250 kHz；选择A0 为主模式，其相速度为2416 m/s，换能器结构为螺旋线圈+圆柱型磁铁；线圈选用双层双分裂结构线圈[12]，实验连接如图4 所示。

图4 焊缝检测实验整体图

通过实验平台捕捉到的回波信息，对裂纹进行估算，其结果见表4。

表4 裂纹定量分析结果

裂纹定量分析结果表明，在一发一收模式下，通过回波幅值变化规则及接收波之间的时间差，能够很好地对裂纹进行定量评估。由于测量结果的读取误差及材料的实际参数与仿真参数的差别，使裂纹定量分析存在一定的误差。

4 结语

对板中Lamb 波电磁超声换能器进行有限元分析，研究了Lamb 波在铝板焊缝中的传播特性，完成了焊缝检测EMAT 的设计并搭建出实验平台。通过仿真分析了不同裂纹处Lamb 波的响应特性，并对裂纹与回波的相位、幅值等特征信息间的关系展开仿真分析，得出了回波幅值、到达时间随裂纹长度、位置的变化曲线，并对其进行了拟合。最后对0.2 mm 的纵向裂纹进行了实验研究，经过数据处理后得到实验结果，结合拟合曲线反演出裂纹信息，表明该装置能够识别裂纹特征，可以对裂纹缺陷进行定位和模糊程度的定量判断，验证了仿真实验的正确性，为基于电磁超声的焊缝检测实验研究以及裂纹缺陷的定量检测奠定了实践基础。