考虑互热影响的直埋电缆温度场解析计算

于坤生，庞 丹，齐明泽，鲁志伟

(1.东北电力大学电气工程学院，吉林 吉林 132012；2.国网吉林省电力公司长春供电公司，吉林 长春 130000)

直埋电力电缆广泛用于电能输送，电缆缆芯的温度是限制其输送能力的关键，对交联聚乙烯电缆而言，绝缘层耐受温度为90 ℃.为了使电缆得到充分应用，且不超过电缆缆芯温度上限，有必要对电缆温度场进行精确且快速的计算[1-4].计算温度场常用方法有数值法和解析法，数值法常借助相关仿真软件求解，可实现温度场精确计算，但对于不同的电缆型号、不同的敷设方式，需要设置相应参数，耗时较长[5]；解析法则通过构建热路模型，用IEC标准公式求解模型中的热阻、热容参数，最终由外界温度叠加各层温升求得缆芯温度，该过程可借助编程工具实现快速计算[6].电缆的规格和排列方式确定之后，土壤的热阻与热容是影响电缆温度场的主要因素，集群敷设时还要考虑周围电缆的互热影响，因此解析法计算直埋电缆温度场的关键在于土壤部分热路模型的正确构建.

计算电缆稳态温度时，IEC标准通过定义绝缘层热阻T1、外护层热阻T3建立电缆热路模型，并用等效热阻T4来模拟电缆周围环境.电缆集群敷设时，求解方法是计算计及电缆间相互热效应对电缆外部热阻T4的修正值.对于埋地电力电缆群，通过镜像法计算其他相邻电缆对研究电缆造成的表面温升，根据电缆不同的敷设类型采用相应的计算公式求得T4，并用叠加法求得缆芯温度[7-9].计算电缆暂态温升时，由于电缆内部热容的存在，导体温度为随时间变化的曲线，IEC标准将土壤的影响和电缆的互热效应包含在扩散方程的解析解中，通过求解指数积分可实现温度场的精确计算[10-14].

文献[15-18]将土壤不均匀地离散为多层，电缆及土壤各层均等效为RC梯形热路模型，并证实了5层土壤模型能正确模拟温度在土壤中的扩散过程.本文通过在土壤梯形热路模型的相应位置添加相邻电缆的损耗来模拟电缆的相互热影响，并将热路模型计算结果与有限元仿真对比，结果表明新模型可准确再现电缆集群敷设时的温度场.与有限元仿真相比，热路模型计算效率高，可通过列写节点热流方程实现快速精确求解.现有的用于分析RC热路的技术都可以应用于该模型，新模型也适用于电磁暂态仿真软件ATP-EMTP，为工程技术人员提供了极大的灵活性，使他们能够使用简单的模型进行快速、准确、高效的分析，无需求解相关的标准方程.

1 考虑互热影响的土壤热路模型

1.1 IEC标准中土壤部分温升的求解

IEC 60853标准规定，相同载荷的电缆组内最热电缆外表面的暂态温升(持续时间大于1 h左右)θe(t)计算式为

(1)

公式中：ρT为土壤热阻系数；WI为电缆组内各电缆单位长度的总功率损耗；De为电缆外径；t为电缆发热时间；δ为土壤散热系数；dpk为相邻电缆k到最热电缆p的距离；dpk′为电缆k的镜像到电缆p的距离；N为电缆组内电缆的数量；指数Ei求解时需要按级数展开.求解稳态温升，即当t→∞时，对公式(1)求解，稳态公式可改写为

(2)

公式中：电缆p表面的总温升Δθp为电缆p中的损耗Wp和相邻电缆中的损耗Wk引起的温升的叠加.

计算电缆自身损耗引起的温升时，外部热阻T4可视为单根电缆敷设时求解

(3)

(4)

公式中：T4为电缆外部热阻；L为电缆轴线至地表距离.

计算相邻电缆的热影响时，第k根电缆单位长度的损耗Wk对第p根电缆所引起的表面温升为

(5)

IEC标准非常精确地模拟了稳态条件下相邻电缆k对研究电缆p造成的温升，为了使公式(5)与电缆各层的热阻表达式一致，可将Δθpk视为等效热阻T4mk，用于表示相邻电缆单位损耗对电缆p产生的热影响，即当Wk=1，互热影响可用热阻表示为(下文均简称互热热阻)

(6)

IEC标准中给出的公式可准确计算稳态时电缆外部温升，但当计算土壤部分的暂态温升时，计算式中包含指数积分，并没有给出与电缆部分相似的RC热路模型，从而不能高效快速地计算.

1.2 土壤模型的构建

土壤指数离散模型可正确模拟温度在土壤中的扩散过程，该模型精确地再现了单根单芯电缆的温度场[15]，证明了模型的可用性.本文将其与IEC标准中的电缆模型结合，提出如图1所示新模型，电缆部分参数参照IEC标准求得，土壤部分各层的热阻热容计算公式为

(7)

(8)

公式中：m为土壤层数，m=1，2，3，4，5；th为土壤各层厚度；rext、rint分别为各层的外径与内径；Cp为土壤的体积比热容.

新模型中的热容Csi可直接由公式(8)求得，热阻Rsi计算式为

(9)

(10)

(11)

公式中：i=2，3，4，5.

图1 单根电缆热路模型

现实中电缆多以集群方式敷设在土壤中，电缆间的互热效应对温度场的影响不可忽略，如果使用热路模型来考虑相邻电缆的热影响，则可以用解析法快速求解所有直埋电缆的温度场，具有重要的工程实用价值.通过在土壤梯形热路特定位置注入相邻电缆的损耗来模拟电缆间的相互热影响[17]，注入位置由公式(3)和公式(6)求得，将所有相邻电缆的互热影响包含在研究电缆p的RC梯形热路模型中，用于求解电缆的瞬态温度，具体的土壤模型如图2所示.

电缆外部热阻T4与电缆埋深有关，互热热阻T4mk受电缆间距和电缆埋深的影响，两者均与电缆的敷设位置有关，相邻电缆造成的损耗Wk应准确地添加到互热热阻所处位置.如果T4-T4m1落在土壤热阻Rs4内，该热阻将被分为两个子热阻Rs4a和Rs4b，它们的值由T4-T4m1计算得出，需在两个子热阻的连接点处添加损耗W1，保证该模型计算稳态温度场的精度；如果相邻电缆的损耗W2注入到累积热阻为T4-T4m2的节点处，可通过在图2中添加热源W2的方式模拟.土壤热路模型基于叠加原理，它可以很容易地外推到相邻的N根电缆，将每根电缆的损耗添加到表示该电缆互热影响的互热热阻所在位置处即可.

图2 考虑互热效应的热路模型

相邻电缆损耗由Wk表示，Wk在土壤模型中的注入点仅取决于稳态热阻值T4和T4mk，其由电缆的几何位置决定，土壤特性由热路模型模拟，电缆的外部温升可用解析法正确求解.新模型能够计算电缆集群敷设时稳态和瞬态条件下的温度场，避免求解相关的指数积分方程，并保留IEC标准中给出的分层模型.根据新模型列写状态空间方程，用经典的4阶Runge-Kutta法编程求得节点热流方程的数值解，可获得各节点任意时刻的温度.

2 模型验证

2.1 稳态温升验证

新模型应能准确计算电缆稳态和暂态温度场，为便于分析，使用两根单芯电缆来验证电缆间的互热影响，并将解析算法与有限元仿真获得的结果进行比较.本文所用单芯电缆型号为YJLW03-64/110kV-1×630，电缆的结构参数如表1所示，电缆各层材料参数可在IEC标准中查到.为简化分析，模型验证中电缆部分热源只考虑缆芯损耗.两根电缆水平敷设在土壤中，土壤热阻系数ρT=0.6 K·m/W，体积比热容Cp=2.5×106J/mm3K，土壤温度Tsoil=13 ℃，电缆埋深为1 m，两根电缆均通以1 210 A的电流，在此电流下单根电缆敷设时可达到90 ℃.两根电缆依次相聚20 cm、100 cm时，COMSOL仿真求得的稳态温度如图3所示，图3中包括电缆温度分布和等值温度曲线两部分，由图可知两种敷设情况下缆芯温度分别为108.0 ℃、99.7 ℃，解析法求得的缆芯稳态温度分别为107.8 ℃、99.6 ℃，稳态温度较单根敷设时有了明显提升，这是互热效应所引起的.由解析计算结果与有限元仿真计算结果对比得知，新模型可用于求解电缆稳态温度场.

表1 电缆各层结构参数

图3 两根电缆不同敷设间距时稳态温度分布图

2.2 暂态温升验证

采用与稳态验证时相同的电缆敷设方式，研究电缆在瞬态条件下的温度变化.左侧电缆(电缆1)在168 h内承受负荷1 200 A，右侧电缆(电缆2)在前60 h内承载600 A，在剩余的108 h内承载1 500 A，根据图2所示模型列写节点热流方程，借助MATLAB编写四阶Runge-Kutta算法求其数值解，并与有限元仿真结果对比.有限元模拟的结果与解析解比较如图4所示，由图4可知，解析解与有限元仿真求得的温度随时间变化曲线基本吻合，准确地模拟了温度在土壤中的热扩散过程.

图4 两根电缆不同敷设间距时考虑互热影响的温度随时间变化曲线

由图4分析可知，当电缆相距20 cm时，施加在电缆2的阶跃电流由600 A上升到1 500 A后，电缆1的温升曲线发生了明显的变化，温度变化率明显提高；当电缆间距100 cm时，温度变化并不明显，如图5所示.前者较后者在施加阶跃电流后的108 h小时内温度提升了12 ℃，由此可见电缆间距较小时的互热影响不可忽略.

平均绝对误差MAE是将解析法和有限元仿真法在各时刻求解结果之间的缆芯温差取和再求平均，表达式为

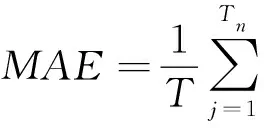
(12)

公式中：tj为模拟的不同时间样本；Tn为样本总数.

以有限元仿真结果为标准，从峰值误差和平均绝对值误差两方面验证新模型求解暂态温度的准确性.了解析法在每一时刻的绝对值误差如图6所示，各敷设情况下的平均绝对误差统计在表2中.由图6可见，负荷变化的节点附近会出现3.2 ℃的峰值误差，且四种情况下的平均绝对误差的最大值为0.57 ℃.误差产生的原因是IEC标准中将电缆绝缘层当作集中参数处理[19].负载快速变化时，绝缘层较低的散热率、较大的径向几何尺寸将会使绝缘层内各点的温升差异很大，此时绝缘层应视作近似分布参数，要实现精确计算应对其进行分层处理.本文主要对考虑互热影响时的土壤模型进行分析，且新模型的计算误差在工程允许范围之内，绝缘层分层对电缆电缆暂态温升的影响将在以后的研究中进一步讨论.周围电缆对研究电缆的影响由电缆间距和周围电缆的总损耗决定，电缆的的总损耗可通过IEC标准实现精确计算，新模型计算中出现的误差并不会随着电缆数目的增多而叠加.由解析计算结果与有限元数值计算结果对比得知，新模型可用于求解电缆暂态温度场.

图5 不同间距下互热影响对比图图6 解析计算的误差曲线

表2 不同情况下的平均绝对误差

本部分对新模型在电缆温度场求解中的适应性进行了讨论，证实模型可应用于工程实际计算中，并结合电缆暂态温升误差曲线对模型提出了改进.新模型补充了现有的电缆暂态温升计算方法，不必计及指数积分便可用解析法求得电缆的实时温度.

3 模型应用

新模型可用于求解电缆集群敷设时各时刻的缆芯温度，以此为依据实现电缆的动态增容.单回路YJLW03-64/110 kV-1×630电缆水平排列敷设在土壤中，电缆金属护套采取交叉互联的接地方式，金属套环流损耗为0，单回路电缆稳态载流量为941 A.三相均通以800 A的电流，持续168 h，电缆部分损耗包括缆芯损耗、介质损耗、金属套涡流损耗，分别采用有限元仿真与解析法求得三相电缆缆芯温度随时间变化曲线，滞后项(C相)与超前相(A相)温度变化曲线相同，A相和B相的温升曲线如图7所示.

新模型可用于确定过负荷等级，告诉操作员在给定条件下可使电缆过载多长时间，并在分析中添加适当的安全裕度，为电力调度部门指导电缆的运行提供理论依据.图7中B相电缆运行60 h时发生过载，时刻电缆温度分布图如图8所示，表3给出了在不同的过负荷下的允许运行时间.过载越严重，允许运行时间越短，考虑到操作裕度，应避免电缆在较高过负荷下运行.

图7 单回路电缆温度随时间变化曲线图8 60h时单回路电缆温度分布图

表3 不同过负荷下电缆达到允许温度所用时间

4 结 论

本文采用电缆热路模型计算了考虑周围电缆互热影响时的电缆温度场，并采用有限元仿真进行了验证.得到主要结论如下：

(1)电缆间距较近时，电缆间的互热影响不可忽略，间距20 cm的两根水平排列的电缆在108 h内较间距100 cm的电缆缆芯温度提升了12 ℃.

(2)新模型能正确模拟电缆稳态温度场和暂态温度场，误差均在工程允许范围之内，其中通以恒定电流时的误差比通以变电流时误差大.

(3)电缆的互热影响作为热源添加到土壤模型中，对模型中各节点列写热平衡方程，可用编程实现对集群敷设电缆温度场的快速准确计算，不必按照IEC标准计算指数积分.

(4)新模型可快速计算电缆在不同过负荷下的应急时间，以数值法计算结果为标准，过负荷越严重计算结果越准确，符合实际操作中的要求.