考虑风电场功率爬坡的超短期组合预测

杨 茂，于欣楠

(东北电力大学现代电力系统仿真控制与绿色电能新技术教育部重点实验室，吉林 吉林 132012)

当前，世界能源结构及其带来的问题正迫使人们寻找新的能源解决方案，清洁、无排放的新能源随之得到了广泛的开发和利用.其中风能是大规模开发利用的最有潜力的清洁能源之一[1-3].由于风能自身的间歇性及波动性等特征，风电场的功率呈现出了一种高度的不确定性，具体表现为风电功率的爬坡事件，这给大规模风电并入电力系统以及电能质量都带来了严峻挑战，因此考虑风电场功率爬坡的预测方法成为了当前研究的重点[4-6].

风电功率爬坡事件是指在较短时间尺度内风功率出现较大幅度波动的情况，这会对区域电能质量及电力调度计划产生一定的消极影响.在我国风电大规模并网的发展模式大前提下，受到地理位置及不规律的自然气候影响的风电功率爬坡现象对电力系统所产生的影响日益突出，考虑风电场功率爬坡的预测是其中的关键环节.

参考文献[7-8]中详细介绍了爬坡事件的几类定义，分别采用了均值聚类算法、支持向量机等方法对历史数据中的爬坡事件进行了不同的分类，并分析了不同类型爬坡事件的各自特征以及危害.参考文献[9]中提出了一种具有自适应选择特征的小波深度置信算法.这种方法在一定程度上可以提高超短期预测的精度，但计算过于复杂并且在风电爬坡事件的漏捕率及误捕率指标上表现不佳.参考文献[10]中提出了一种考虑风电场爬坡事件的基本模式及其自相关统计特性的模型，建立了一种关于爬坡事件的日前预测算法.该方法尽管有效减少了预测过程中误报及漏报的情况，但其仅包含了风电场的历史功率数据，同样没有考虑未来的天气因素，导致了预测的局限性.

目前，超短期风电功率预测更多的是直接使用功率时间序列来构建预测模型[11-13]，但这类预测模型无法很好地追踪风电功率的波动情况.而风速因素是引起功率出力变化的主要因素，当风速在短时间内变化较大时，仅根据历史功率信息无法对未来的变化趋势进行判断，从而导致较大的预测误差.文献[14-15]是在考虑风电功率爬坡事件和预测难度大等条件时，建立了考虑风电爬坡事件约束的精确线性化的机组组合模型，但其性能受爬坡波动速率的约束.文献[16-17]所运用的是基于时间序列法的风电功率波动分析及预测，该方法可以对超短期的风电功率进行预测，具有一定的实用价值，但其无法从宏观角度去审视风电功率的波动特性.文献[18-19]提出在一个合适的时间窗口内进行风电功率预测和爬坡事件识别的方法，并重点讨论如何选取合适的预测时间窗，通过多个评估指标验证了该预测时间窗对实例爬坡预测的有效性.该工作为爬坡事件的预测奠定了重要基础.但是针对风电功率爬坡预测的预测精度还有待进一步提高，且结合数值天气预报气象因素的爬坡预测研究较少.

为此，针对上述问题本文采用极限学习机理论，引入NWP中的有效信息，提出了一种考虑风电场功率爬坡的超短期功率组合预测方法.根据已知的数值天气预报(NWP)序列，利用灰色关联识别出与风电功率相关性较强的几个天气因素，对其中相关性最强的天气因素根据爬坡事件的定义进行划分，在其发生爬坡事件时引入数值天气预报(NWP)信息作为输入变量，并采用极限学习机算法预测未来的风力发电量.最后，采用吉林省内某风电场的实际测量数据进行验证，计算结果表明，本文所提出的方法可准确识别风电的爬坡事件并削弱其给预测结果带来的影响，同时能够有效地提高风电场功率超短期预测精度，验证了该方法的有效性.

1 风电爬坡事件分析

1.1 爬坡事件定义

在目前日渐繁杂的风电应用需求下，不同区域的风电场应当结合其实际需求及场站特征来建立合适的风电爬坡事件的具体定义，这是实现其有效预测亟待解决的问题.目前大多数预测爬坡事件的方法是含统计及物理模型的方法，而如何从包含各种不确定因素的复杂历史及气象数据中提取出关于爬坡事件的特征，并同时满足预测爬坡事件精度的要求是目前主要的发展方向[20-21].

目前相对较为常见的风电爬坡事件定义有3种[4]，本文所使用的定义是目前应用相对广泛的一种.假设在风电功率数据某时间区间ΔT的开始时刻，当此区间的功率增加或减少的幅值大于预先设定的阈值参数Trval时，则认为在此ΔT时间区间内发生了功率爬坡事件，计算方法表示为

|P(t+ΔT)-P(t)|>Trval.

(1)

本定义考虑了该时间段首末段的风电功率值，涵盖了大部分的风电爬坡事件，应用最为广泛.

1.2 灰色关联

在数值天气预报数据中，不同的天气因素对风电功率预测的影响程度不尽相同.为了提取出数值天气预报中与风电功率相关性较高的天气因素来作为输入变量，采用灰色关联分析(gray relation analysis，GRA)方法来提取数据，计算其中的各个特征与风电功率的关联度，并选取关联度较高的几个天气因素作为输入建立爬坡预测模型.NWP中的各个特征及其与风电功率的灰色关联度如表1所示.

表1 NWP 特征及其对应灰色关联度

从表1中可以看出100 m风速与风电功率的相关性最高，因此采用100 m风速数据作为判断爬坡事件的输入；同时采用关联度较高的几个天气因素作为风电功率爬坡段的输入，以更好地跟踪风电功率的波动趋势.

2 风电爬坡预测模型的建立

本文基于极限学习机理论，提出了一种考虑风电场功率爬坡的超短期组合预测模型，具体步骤如下：

读取风电功率数据及数值天气预报(NWP)数据，利用灰色关联分析方法提取与风功率相关性较强的多维气象因素数据.

选取NWP数据中相关性最强的100 m风速数据，利用公式(1)所示的爬坡事件的定义判断其是否发生爬坡事件；

如果未发生爬坡事件，则输出其对应风功率段作为预测输入，采用ELM方法进行预测得到预测值P1；

如果发生爬坡事件，则输出其对应风功率段，同时将与其相关性较强的风速、风向等多种气象因素数据一起作为预测输入，建立ELM-NWP-C预测模型进行预测得到预测值P2.

将预测值P1及P2进行组合加权，并采用国家能源局文件风电功率预测功能规范中的评价指标进行结果分析；得到最终的风电功率预测值P.

详细的建模流程图如图1所示.

图1 组合预测模型流程图

3 算例分析

3.1 数据描述

本文采用2018年吉林省二十个风电场集群的实际测量数据作为样本来进行分析，其采样间隔为15分钟，风场的总装机容量为2 854.31兆瓦.算例选取2018年1月1日至6月30日共181天的实测数据作为训练集，2018年7月1日至7月31日共31天的数据作为测试集，对所提方法进行验证.

3.2 评价指标

本文采用国家能源局文件《风电功率预测功能规范》中的评价指标[25]：日平均准确率r1、日平均合格率r2、日预测均方根误差r3来对预测结果进行评价分析.各个指标的计算公式如下所示.

日平均准确率r1：

(2)

公式中：r1i为第i次实时预测的准确率，且

(3)

日平均合格率r2：

(4)

公式中：r2i为第i次实时预测的合格率，且

(5)

(6)

日预测均方根误差r3：

(7)

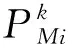
3.3 实验结果分析

本文为了对比验证所提ELM-NWP-C模型对超短期风功率预测的精准性和有效性，分别选取极限学习机神经网络(extreme learning machine，ELM)模型、反向传播神经网络(backpropagation，BP)模型、长短期记忆神经网络(long short-term memory，LSTM)模型作为对比模型来进行分析，不同方法的预测误差如表2所示.

表2 7月平均预测误差对比

靠近预测开始的时段时，仅以功率特征作为输入进行预测的方法具有更大的优势，对于每次滚动预测的16个点全部进行误差统计就无法合理地比较各方法的优劣，因此本文仅对第16个时点的预测精度进行统计.从上述指标统计结果可以看出，相比于只考虑历史功率的分析方法，本文所提出的方法在预测数值的准确程度上要高于其他方法，准确率平均提高了2.67%，合格率平均提高了8.45%.采用NWP作为输入特征的方法准确率普遍高于仅输入功率进行预测的方法，即其在风电功率趋势的跟踪上要更具优势，说明考虑风电场功率爬坡过程能够有效地提高预测精度.

本文所提ELM-NWP-C模型与三种常见预测模型的预测值与实际值进行对比分析，预测对比结果见附录图A.由图A对比可以看出基于ELM-NWP-C模型的超短期风功率预测结果曲线拟合效果最好，预测精准度最高，预测效果最好.考虑了天气因素的功率爬坡预测模型曲线精准度优于未加入天气因素的ELM模型，说明天气因素对发生功率爬坡时的优化有明显的促进作用.本文仅截取其中三天的预测曲线与实际曲线，如图2所示.可以看出本文所提方法可以有效识别并跟踪风电功率的波动变化.

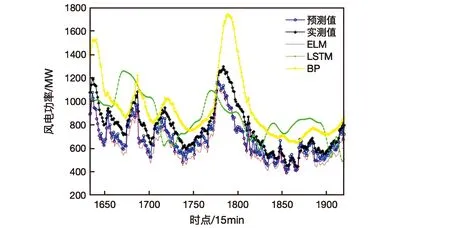
图2 2018年7月某三天预测效果对比图

由于每天的风速分布都不尽相同，因此以大风日，中风日和小风日来对预测结果进行分类分析，以保证所提方法的严谨性.利用NWP中的100米风速数据将预测数据集划分为大风，中风，小风出力场景，再对各场景的精度进行分析.根据日平均风速对天气类型进行划分，分为大风日，中风日，小风日.对风速数据区间进行划分，将日平均风速区间在7 m/s～10 m/s的日期定义为大风日，日平均风速区间在4 m/s～7 m/s的日期定义为中风日，日平均风速区间在1 m/s～4 m/s的日期定义为小风日.本文选取的数据集中大风日为11天，中风日为8天，小风日为12天.几种建模方式在不同风期的评价指标如表3所示.

表3 预测模型平均对比分析

由表3可以看出，本文所提方法的预测效果最佳，在不同风期下，均能得到较高的准确率和拟合效果.在大风日，相对于ELM、BP及LSTM模型，ELM-NWP-C准确率分别提高1.38%，4.07%，1.44%；合格率分别提高8.17%，14.58%，10.04%；中风日时相对于ELM、BP及LSTM模型，ELM-NWP-C均方根误差分别降低2.08%，4.98%，1.65%，合格率分别提高了8.99%，17.16%，8.63%；小风日时普遍表现较好，所有方法在小风日预测准确率均大于90%，但ELM-NWP-C模型仍然具有明显优势，相对于ELM、BP及LSTM模型准确率分别提高了4.18%，0.90%，3.29%，合格率分别提高了3.71%，1.23%，3.55%.从表中可以看出本文所提方法可以显著提高预测精度，且合格率均满足要求，可以更好地追踪爬坡趋势.

为了进一步验证模型的有效性，分别选取大风日、中风日、小风日中预测表现相对较好的一天及相对较差的一天进行对比分析，结果如表4及表5所示.

表4 预测模型分风期较高一天对比分析

表5 预测模型分风期最低一天对比分析

为了更清晰地体现出本文所提方法相较于其他常用预测方法的优势，图3及图4给出了风电场分风期较高一天及较低一天的功率实际值与各个预测值的对比效果，用于直观评判各模型的预测效果.

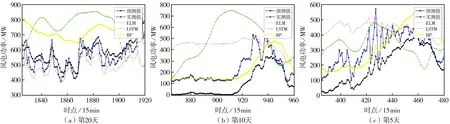
图3 预测模型分风期较高一天对比图

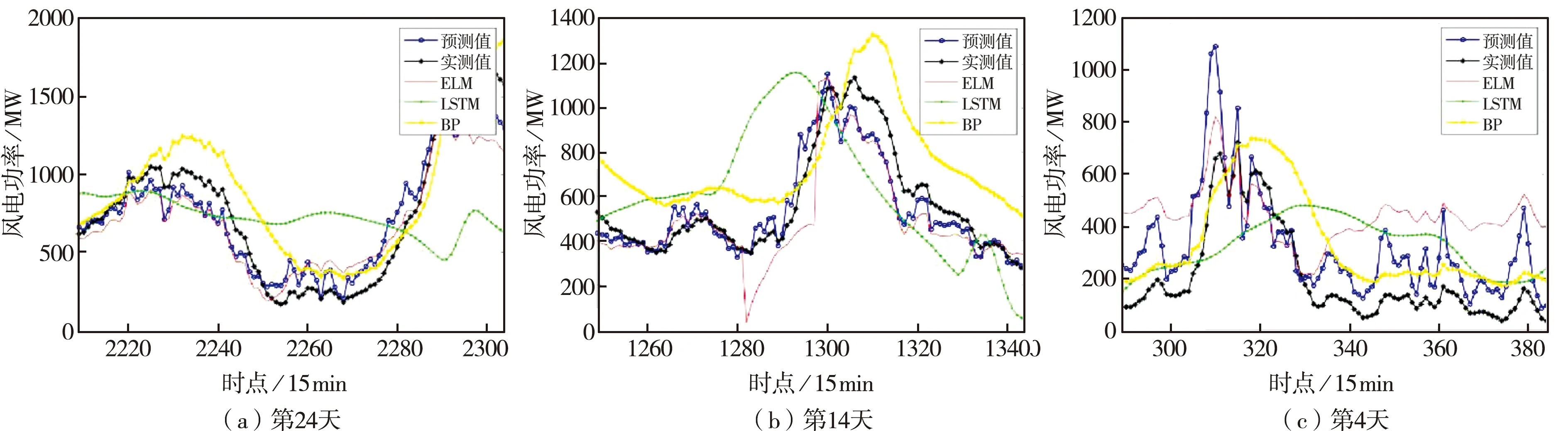
图4 预测模型分风期较低一天对比图

由图3和表4可知，本文方法的预测值与实际值拟合较好，无论在大风日、中风日还是小风日都能够在风电功率波动时跟随其波动趋势.而ELM及BP模型虽然也可以跟踪功率变化趋势，但效果十分不稳定，且部分天数拟合较差，总体效果不及本文方法；LSTM模型的预测值则较为平缓，不能很好地跟随功率数据波动，说明仅选用历史功率作为预测模型输入时无法有效追踪功率波动趋势，而考虑NWP信息作为输入则可充分利用其中的有效信息，改善模型的预测效果.由图4和表5可知，在同一风期下，ELM-NWP-C预测模型能够紧紧跟随风电功率的波动趋势从而得到更精确的预报值，以提供更加精确的预报信息.从整体上可以看出，所提预测方法是极具优势的.

4 结 论

为了弥补单一输入特征的预测模型在风电场发生爬坡事件时的不足，本文提出了一种基于极限学习机理论的考虑风电场功率爬坡的超短期组合预测模型.通过实际算例分析，得到如下结论：

考虑天气因素的预测模型可以更好地跟踪识别风电功率的爬坡趋势，因而引入NWP信息可以在一定程度上弥补仅采用功率作为输入特征的预测模型所带来的负面影响.采用实际生产数据进行计算的算例结果表明，与ELM、BP、LSTM等常见预测模型相比，考虑风电场功率爬坡事件的超短期组合预测算法可以有效地利用NWP信息，其预测结果有着较高的精度.

图A 2018年7月各模型预测值与实际值对比结果