基于DTW-KNN的机械通气无效吸气努力检测
2022-09-06方路平葛慧青
潘 清 龚 强 陆 飞 方路平 葛慧青
1(浙江工业大学信息工程学院 浙江 杭州 310023)2(浙江大学医学院附属邵逸夫医院呼吸治疗科 浙江 杭州 310016)
0 引 言
重症监护室(Intensive Care Unit, ICU)是保障重症病人生命活动的最后一道防线。呼吸机是ICU里最重要的生命支持设备[1]。为最大程度保证病人生命安全,正确使用呼吸机,确保高质量的人机交互至关重要[2]。但是,使用呼吸机进行辅助通气的重症病人的生理呼吸周期与呼吸机的送气周期可能不一致,会产生人机不同步现象[3]。人机不同步在呼吸机使用过程中出现频率较高[4-8]。文献[5]研究结果显示,异步指数(不同步事件除以总呼吸率)大于等于10%的患者约占呼吸机治疗人数的24%。人机不同步可能会导致患者与呼吸功能高度相关的肌肉组织损伤,进而导致吸气相关的肌肉无法提供正常吸气时所需的力量,造成患者无法脱离呼吸机独立呼吸等诸多病人无法接受的后果[9-10]。研究自动检测机械通气人机不同步能够及时提示医护人员调整呼吸机的各项参数设置,减少人机不同步的发生,改善病人预后,对ICU临床工作具有重要的意义。IEE是最常见的人机不同步类型之一,其在呼吸机波形上的表现为气道压力波形呼气相凹陷的同时伴随流速波形在呼气相突起。由于病人的病情及每一次呼吸的状态均存在不确定性,造成IEE事件的发生程度以及在呼气相的发生时间有所差异,导致IEE特征的幅值、特征在呼气相的位置有所变动,使得IEE事件的气道压力以及流速波形具有非平稳特征。而且,病人呼吸周期存在变异性,将导致呼吸序列不等长。常用的IEE检测方式是依靠专业人员在床边观察和评估呼吸机波形[11-12]。早期IEE的自动检测方法主要是基于规则的[5,13]。Thille等[5]将IEE定义为气道压突然下降(≥0.5 cmH2O)的同时流速也随之降低,并且呼气期间产生的吸气努力强度不足以触发呼吸机为患者送气,无法开启新的呼吸周期。Chen等[13]认为,在呼气期间,当最大流速偏差或者最大气道压偏差超过预设阈值时,即发生IEE事件。近年来,随机森林(Random Forest,RF)及自适应增强(Adaptive Boosting,AdaBoost)算法也被一些学者应用于IEE的自动检测,取得了较好的效果[14]。但上述方法在IEE检测上均存在一定局限性:在床边观察和评估呼吸机波形的方法需要花费大量的医护人员资源;基于规则的检测方法对噪声比较敏感,且其性能受阈值选择影响较大;基于RF和AdaBoost的检测方法需要提取特征,而所提特征可能存在信息泄露的问题。为解决上述方法在IEE检测上的不足,本文提出一种基于DTW-KNN的IEE检测方法,该方法通过计算样本间的相似性对呼吸波形进行分类。
DTW算法基于动态规划的思想,解决了不等长序列的模板匹配问题[15],适用于不等长序列的相似性测量。各种基于DTW方法已成功用于心电信号、脑电信号等生物信号时间序列及非生物信号的分类与识别中[16-19]。文献[16]使用DTW对ECG帧进行模板匹配,实现ECG信号的帧分类,实验达到了1.33%的分类残差的良好分类结果。文献[17]中,DTW更是成功地区分了各种心律不齐的心电信号。以上研究结果证明DTW在具有非平稳特征的生物信号分类中具有良好的性能。
因此,针对呼吸序列的不等长及非平稳特征的问题,本文引入DTW算法计算呼吸序列之间的相似性距离,以此来度量两条序列的相似性。在同一实验数据下,基于规则的方法和AdaBoost方法检测IEE事件的准确率均不足90%。RF的IEE检测准确率为92.5%。而本文提出的DTW-KNN算法对IEE的检测准确率达到96.9%。
1 基于KNN和DTW的IEE检测算法
1.1 IEE波形特征
IEE是最常见的人机不同步类型之一,其气道压力波形与流速波形均存在相应特征:气道压力波形呼气相凹陷,与此同时流速波形在呼气相突起。由于患者的病情和呼吸状态存在不确定性,造成IEE事件的发生程度以及在呼气相的发生时间有所差异,导致IEE特征的幅值、特征在呼气相的位置有所变动,使得IEE事件的气道压力及流速波形具有非平稳特征。而且,病人呼吸周期存在变异性,将导致呼吸序列不等长。
连续五次呼吸的气道压力波形、流速波形及波形特征如图1所示,其中IEE波形特征由黑色圆圈标出。可以看出,IEE事件的呼气相波形与非IEE呼吸相波形相比,两者之间的形状差异较大,并且两个IEE事件之间的特征表现也有所不同,即气道压力以及流速波形具有非平稳特征。

(a) 气道压波形
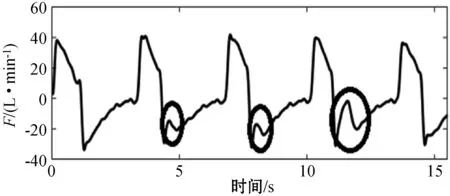
(b) 流速波形图1 连续五次呼吸波形
1.2 数据预处理
在临床上,针对病人不同的病情,需要给予不同强度的机械通气支持,即不同病人的气道压力和流速水平均不相同,这将导致后续使用DTW计算两条呼吸序列的相似性距离产生较大偏差。图2展示了呼吸序列经过预处理与未经过预处理的两条IEE序列及IEE序列、非IEE序列之间的DTW距离,其中:图2(a)、(b)分别给出了未经预处理的两条IEE序列以及IEE序列、非IEE序列之间的DTW距离;图2(c)、(d)分别给出了经过预处理的两条IEE序列以及IEE序列、非IEE序列之间的DTW距离。可以看出,未经过预处理的两条IEE序列的DTW距离为441.94,大于IEE序列与非IEE序列之间的DTW距离411.59;而经过预处理之后的两条IEE序列的DTW距离为10.92,小于IEE序列与非IEE序列之间的DTW距离18.51。由上述结果可知,对呼吸序列进行预处理之后在进行相似性距离计算时,得到的结果更能反映真实的波形相似情况。
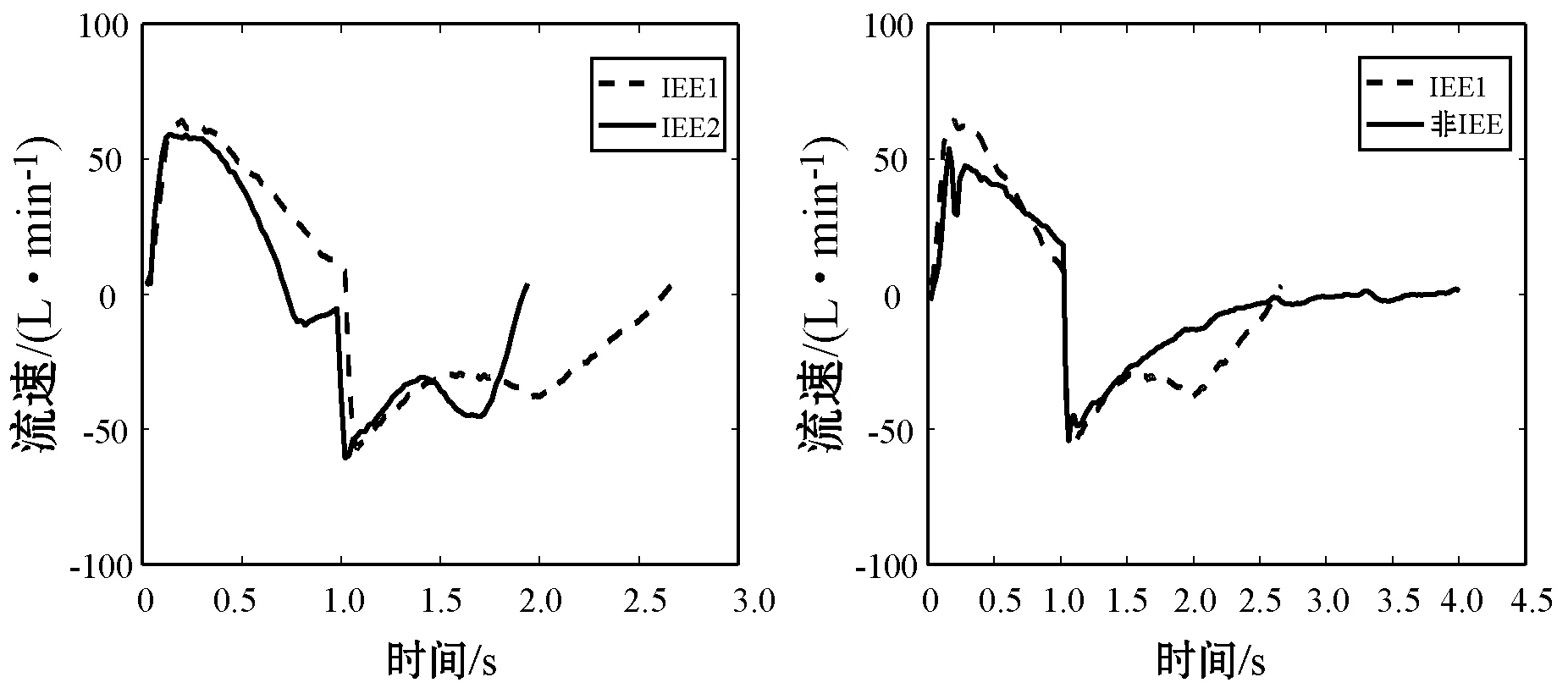
(a) DTW距离:441.94 (b) DTW距离:411.59
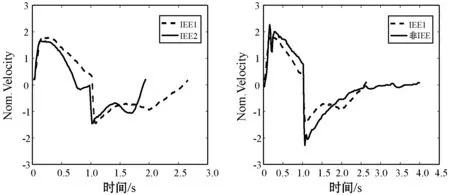
(c) DTW距离:10.92 (d) DTW距离:18.51图2 预处理前后两条同类别序列以及不同类别序列之间的DTW距离对比
因此,在进行数据分析之前需先对波形进行归一化,消除由于波形幅度不同而造成的差异。本文根据式(1)对呼吸序列S(s1,s2,…,sn)采用Z-score方法进行数据标准化,避免因气道压力、流速水平不同引发的问题。
(1)
1.3 K-最邻近算法(KNN)
KNN算法[20]思想简单明了,分类准确率较高,错误概率的上限是贝叶斯错误概率的两倍,被认为是向量控件模型下最好的分类器,在医学以及图像识别与分类等领域都展现其良好的分类效果[21-22]。其基本思想是:计算待分类样本与各个训练样本之间的相似性,找出训练样本中与待分类样本最相似的K个样本,最后根据得到的K个样本的类别确定待分类样本的归属。其算法描述为:首先,计算测试序列样本与各个训练数据样本之间的相似性距离,并按照从小到大的顺序对所有相似性距离进行排序;然后,选取前K个最小距离所对应的测试序列样本,确定所选取的前K个最小距离所对应的测试序列样本所在类别的出现频次;最后,将出现频率最高的类别作为测试出序列样本的预测分类。图3为KNN在本研究中分类示意图,其中:矩形和三角形分别代表不同类型的呼吸波形数据,圆形为待分类呼吸波形。
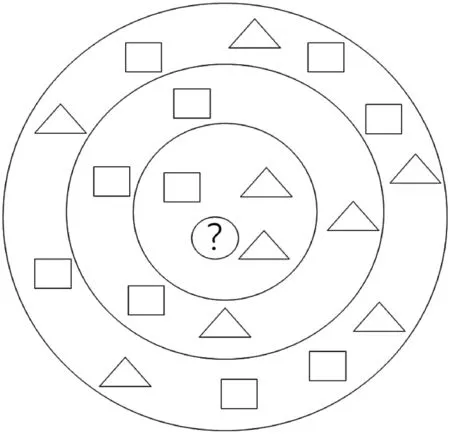
图3 KNN算法示意图
待分类样本与2个三角形样本和1个矩形样本最相似,根据KNN算法,待分类样本被分为三角形样本。同时,对于不同的K值,KNN算法的分类结果是不一样的。
1.4 动态时间规整(DTW)
在KNN算法中需要计算样本之间的相似性。欧氏距离是最常用的样本相似性度量方法。等长时间序列Q(q1,q2,…,qn)和C(c1,c2,…,cn)的欧氏距离ED(Q,C)计算公式如下:
(2)
应用式(2)要求进行对比的两样本之间具有相同的序列长度。但是,由于病人呼吸周期存在变异性,导致采集的呼吸序列长短不一,因而无法使用欧氏距离来度量序列的相似性。通过插值和重采样的方法尽管能够使两段序列具有相同的长度,但插值和重采样方法仅仅使不等长序列变成等长序列而已,并未考虑到两条序列采样点之间的距离的相对大小关系,从而导致了序列各个采样点之间的无规则偏移,进而造成两条序列相似部分采样点之间无法较好地对齐,使得原本相似的两条序列之间的相似性距离偏大。DTW算法基于动态规划的思想,解决了不等长序列的模板匹配问题,适用于不等长序列的相似性测量。各种基于DTW方法已成功用于心电信号、脑电信号等生物信号的分类与识别中。文献[16]使用DTW对ECG帧进行模板匹配,实现ECG信号的帧分类,实验达到了1.33%的分类残差的良好分类结果。在文献[17]中,DTW更是成功地区分了各种心律不齐的心电信号。以上研究结果证明DTW在具有非平稳特征的生物信号分类中具有良好的性能。因此,对于同样具有非平稳特征的呼吸信号,本文以DTW距离来度量不等长呼吸序列之间的相似性。对于两条不等长时间序列Q(q1,q2,…,qn)和C(c1,c2,…,cm),DTW通过动态规划能够找到Q和C之间的最佳规整路径,再通过式(3)得到最小累加距离D(i,j)。
(3)
式中:d(qi,cj)=(qi-cj)2。最终,可由式(4)计算两序列的DTW距离DTW(Q,C)。
(4)
对于两条序列Q(q1,q2,…,qn)和C(c1,c2,…,cm),两者经过动态规划算法得到的最佳规整路径WP={WP1,WP2,…,WPk},max(m,n)≤k≤m+n-1,必须严格服从以下约束:
(1) 边界条件。所选的路径必须从WP1=(1,1)出发,在WPk=(n,m)结束。
(2) 连续性。如果路径当前点为(x1,y1),那么对于路径的下一个点(x,y)需要满足(x-x1)≤1且(y-y1)≤1。
(3) 单调性:如果路径当前点为(x1,y1),那么对于路径的下一个点(x,y)需要满足(x-x1)≥0和(y-y1)≥0。
图4为两条不等长呼吸序列及两者的最佳规整路径。其中:图4(a)、(b)为标准化的呼吸流速序列,图4(c)为最佳规整路径。可以看出,动态规划对时间上的压缩和延伸是不敏感的。因此,采用了动态规划思想的DTW能很好地度量两条不等长序列的相似性。
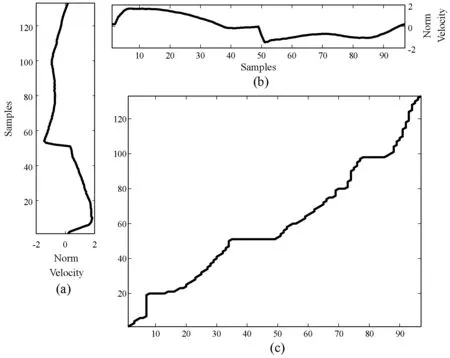
图4 不等长呼吸序列的最佳规整路径示意图
图5为Z-score标准化之后两条呼吸流速序列、经过重采样对齐、插值法对齐以及DTW对齐前后的对比图。可以看出,当采用重采样以及插值法实现两条不等长呼吸流速序列的对齐时,如图5(b)、(c)所示,这两种方法并没有把波形的相似部分较好的对齐,尽管两条序列的长度变得一样,但是波形的对齐效果比图5(a)中直接标准化之后的波形对齐效果还更差。而两条不等长序列经过DTW之后,相比于重采样和插值法的对齐效果,两条原本相似的不等长的呼吸流速序列的对齐效果提升较大,其对齐效果如图5(d)所示。
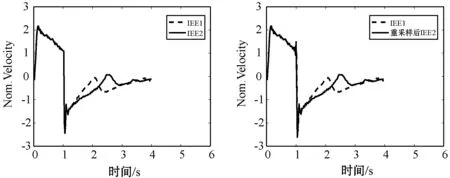
(a) 两条原始呼吸流速 (b) 经过重采样方法对齐的呼吸流速
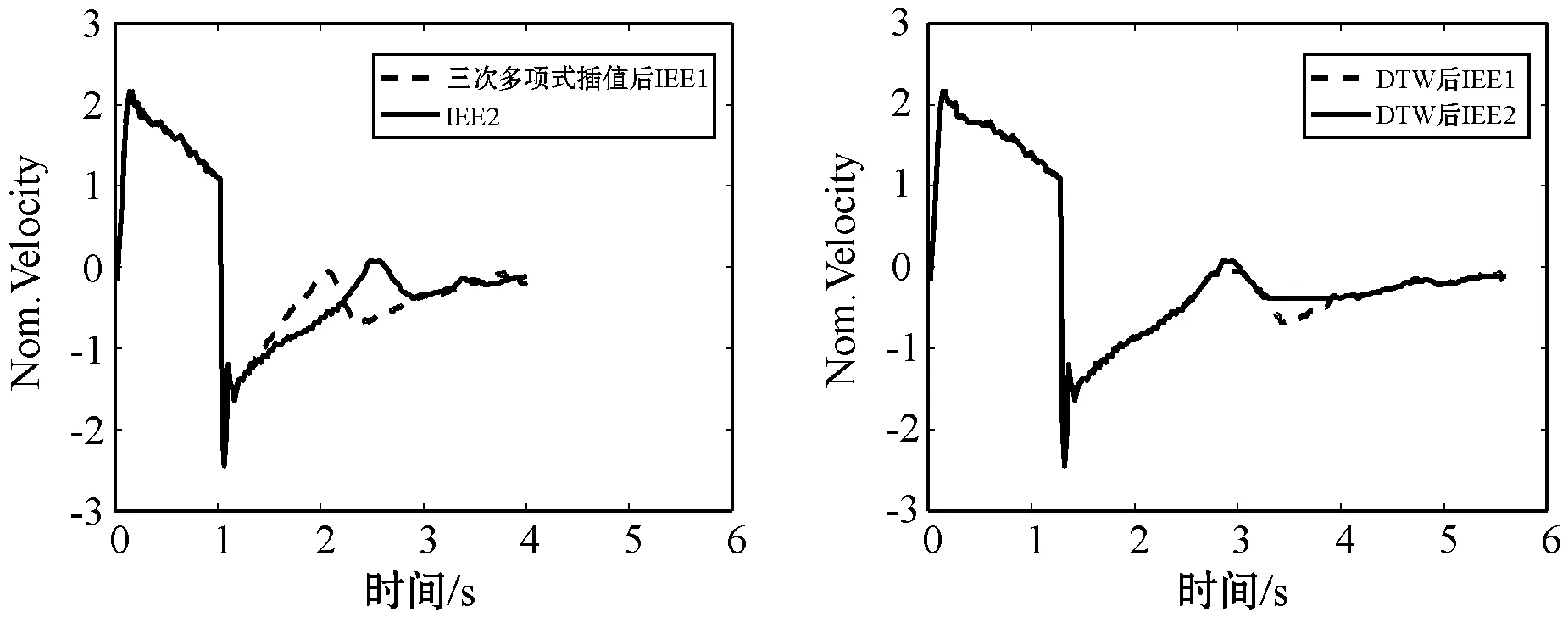
(c) 经过插值法对齐的呼吸流速 (d) 经过DTW对齐的呼吸流速图5 呼吸流速对齐方法对比图
因此,经过DTW对齐之后,能够很好地度量两条序列的相似性距离,从而可以用于KNN算法中的相似度度量。
1.5 实验材料
在重症监护室中采集了17名使用Puritan Bennett 840呼吸机进行机械通气的重症患者的气道流速波形数据。其中成年男性11名,成年女性6名,患者平均年龄为64.5岁。研究得到浙江大学医学院附属邵逸夫医院伦理委员会审查通过(No.20190916-16)。表1展示了所选病人的相关信息。
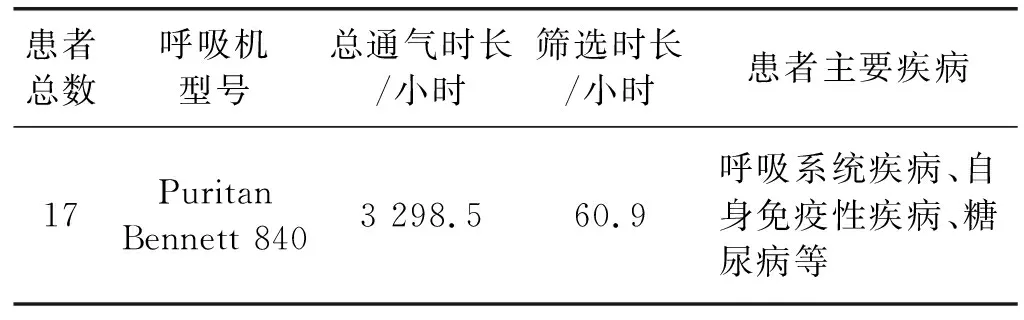
表1 选取病人信息表
对上述筛选的数据进行标注,先由5名资历较低的医生进行第一轮的预标注,后由2名资历较高医生对第一轮的标注结果进行审核,以确保标注结果的准确性。最后形成IEE数据集和非IEE数据集两个数据集,IEE数据集中包含1 032次呼吸流速波形数据,非IEE数据集中包含1 031次呼吸流速波形数据。
1.6 评价方法
本文以十折交叉验证评价算法的性能。将标注后的数据随机分为10份,选取其中1份作为测试序列样本,其余9份作为训练序列样本;然后依次对每一份测试序列样本与训练序列样本分别做Z-score标准化后,再通过DTW计算两者的相似性距离,选取前K个最小距离的训练序列样本;最后将其中出现次数最多的类别标签作为测试序列样本的类别标签。图6为本研究方法流程。
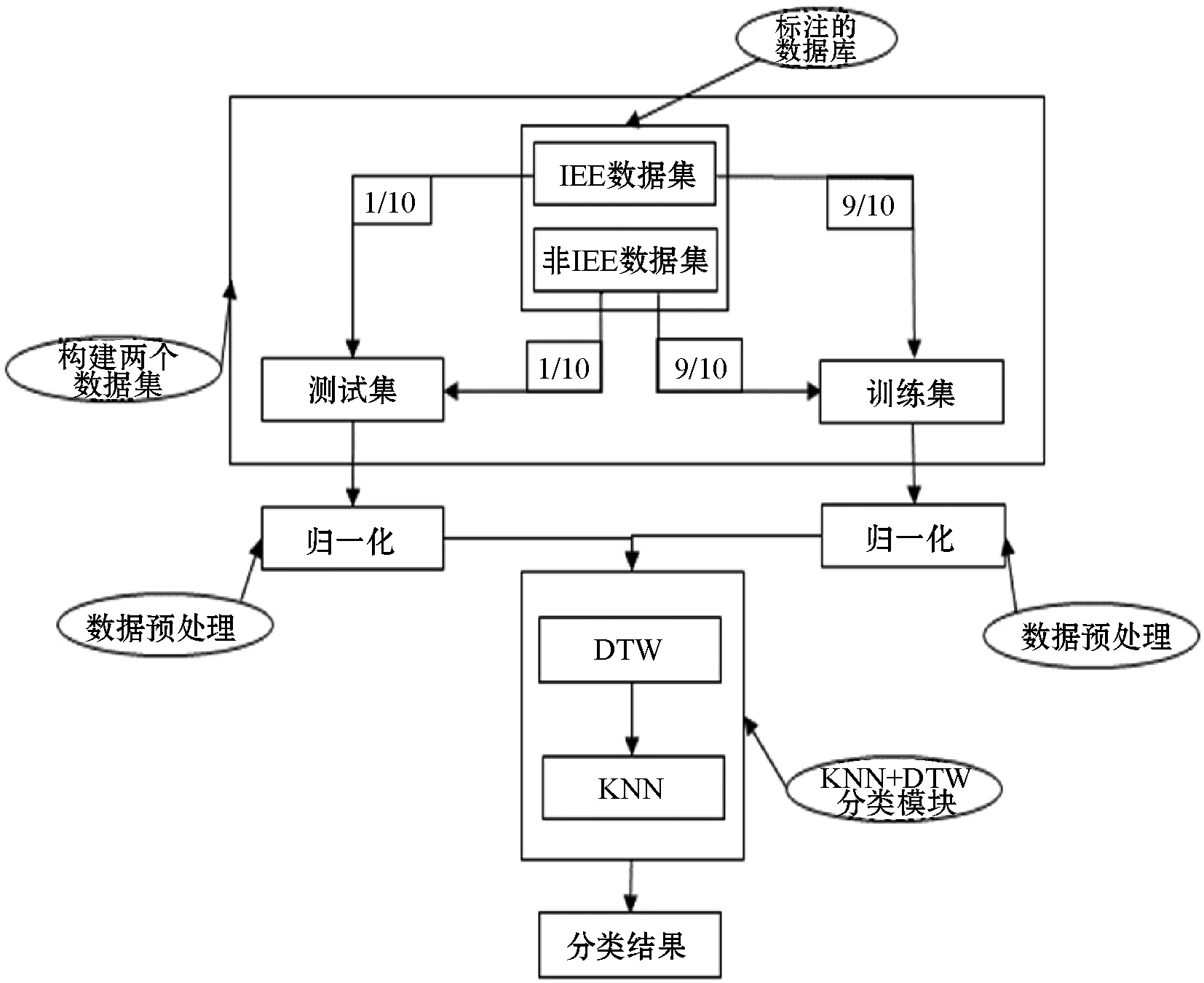
图6 研究方法流程
本实验采用准确率、灵敏度、特异性以及F1得分来衡量算法性能。各指标计算方式如下:
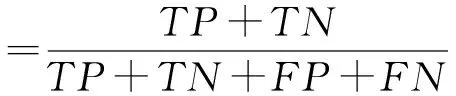
(5)
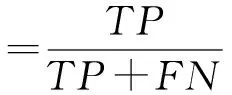
(6)
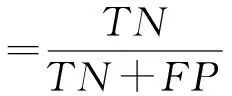
(7)
(8)
式中:TP表示真阳性数量;TN表示真阴性数量;FP表示假阳性数量;FN表示假阴性数量。
1.7 算法对比
为了验证所提出的算法的优越性,本文将其与传统的基于规则的算法及基于RF和AdaBoost的算法进行对比。
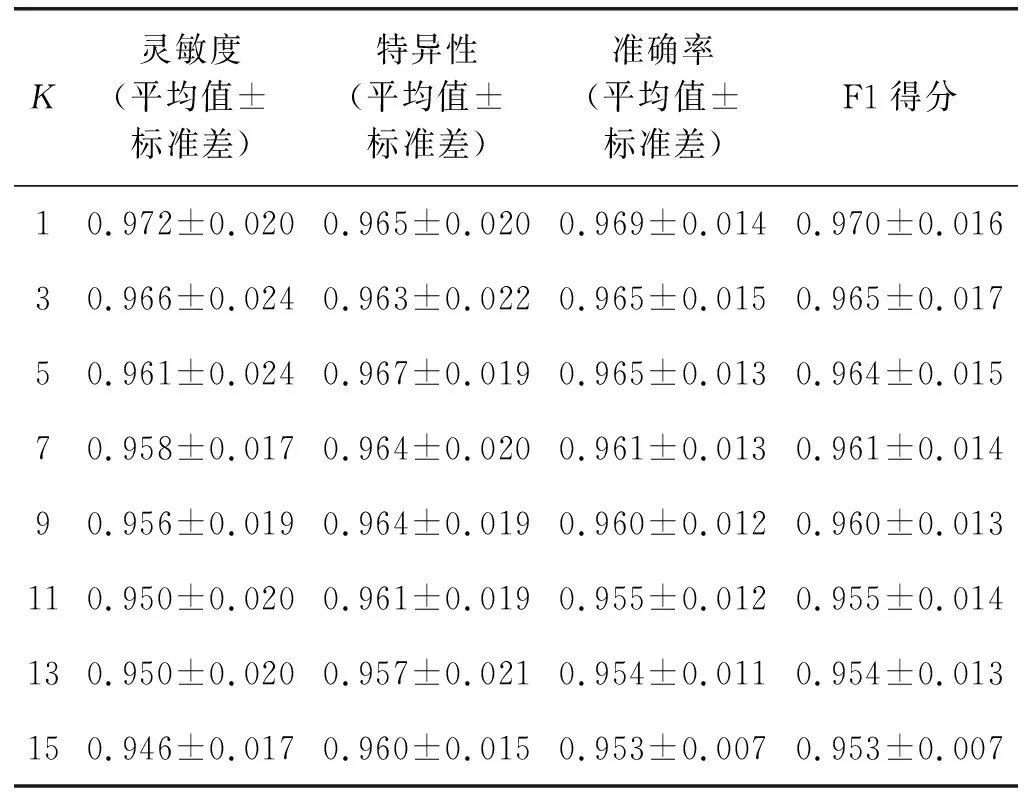
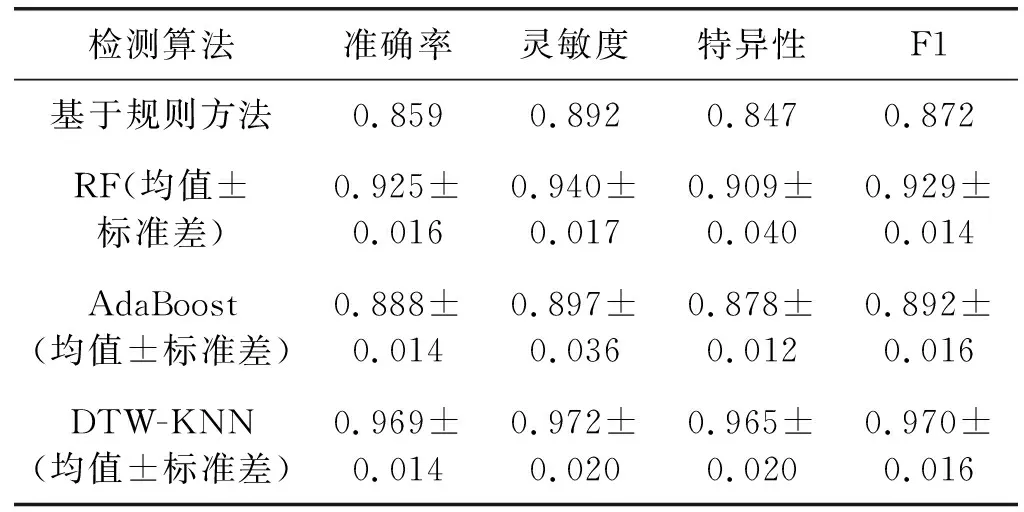
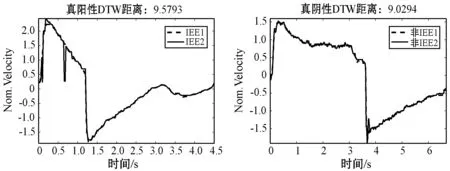
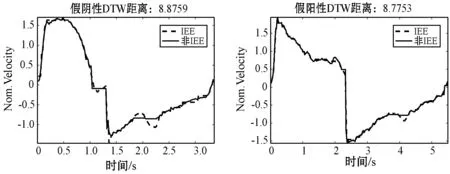
Chen等于2008年提出一种基于规则的IEE检测方法,其基本思想是:通过计算呼吸流速呼气相的极大值与其之后的最小值的差值和设定阈值的大小关系来检测该次呼吸是否发生IEE事件。该算法描述为:首先检测呼吸流速序列的呼气开始点,获取流速呼气相序列H(h1,h2,…,hk),并计算H的所有极大值Hm及极大值索引m,1 Sottile等[14]利用RF算法和AdaBoost算法实现了IEE的自动检测。本文重现了其算法并应用于本文数据集上进行性能对比。首先,提取IEE检测所需的特征,包括呼吸周期、吸气末气道压、吸气末流速、吸气末潮气量等时间、气道压、流速及潮气量四大类特征参数(具体参数见文献[14]的附录补充材料)。随后构建RF和AdaBoost预测模型,通过网格搜索方法进行模型参数调优。最后基于所构建的模型对测试样本进行类别判定。RF基本思想是:从训练集中随机有放回地抽取与训练集数目相等的样本以及随机选取特征集里面的少量IEE特征来对决策树进行训练,反复执行,产生多棵决策树;将未参加决策树训练的训练集样本作为测试样本,再基于少数服从多数原则,对所有决策树的输出结果进行投票以得到测试样本的预测分类结果。AdaBoost基本思想是:根据训练集中每个样本的分类是否正确以及最后一次整体分类的准确性来更改数据分布并确定每个样本的权重。权重已修改的新数据集将发送到下一个弱分类器进行训练,最后算法将组装这些不同的弱分类器以形成更强的分类器作为最终决策分类器。 为验证本文提出方法的性能,将本文方法与Chen等[13]提出的基于规则的方法及Sottile等[14]提出的基于RF和AdaBoost的方法进行比较。 本文算法中,K取1~15(步长为2),不同K值结果在表2中展示。在各种K取值情况下,准确率有所差异,随着K值的增大,准确率逐渐下降,但均在95%以上。K=15时准确率最低,为95.3%;K=1时准确率最高,为96.9%。这表明,IEE样本类内差异范围较大,而与非IEE样本的类间差异范围不大,K取较大值时容易出现部分IEE波形与较多的非IEE样本更相似而错分的情况。 表2 基于DTW-KNN方法在不同K值下对IEE的检测性能 最优DTW-KNN方法与其他方法比较的结果如表3所示。基于规则的方法和AdaBoost方法检测IEE事件的准确率均不足90%。RF的IEE检测准确率为92.5%。本文提出的DTW-KNN算法对IEE的检测准确率达到96.9%,优于其他方法。 表3 实验对比结果 本研究也尝试对检测结果里面的误分样本进行分析。图7为使用DTW-KNN算法对不同呼吸流速序列测试样本进行检测的分类结果示意图。图中的训练数据样本均为测试样本与训练集所有样本的最小DTW距离样本。图7(a)、(b)分别为IEE事件的正确检测与非IEE事件的正确检测示意图,图7(c)、(d)分别为IEE事件与非IEE事件的错误检测示意图。可以看出,经过DTW对齐之后的两个不同类别的序列样本只是在IEE事件呼气相流速波形特征表现处有微小的差异,在波形其他地方基本没有差别。这表明,IEE事件各个亚类样本之间的差异比较明显,而IEE事件各个亚类与非IEE事件样本之间的差异较小。当某个IEE事件亚类中只包含单条呼吸序列样本的时候,将会导致该IEE事件亚类的单条序列样本与非IEE事件的样本的相似性距离达到最小,造成DTW-KNN算法发生呼吸序列样本的错误检测。 (a) (b) (c) (d)图7 样本分类结果图 本文提出的基于DTW-KNN的IEE检测方法相比于文献报道的其他方法更加简单,无须设置各类参数或提取复杂的特征,且准确率更高。基于规则的机械通气IEE检测方法需要选择合适的阈值方能达到最佳效果。RF、AdaBoost等方法需要人工提取波形特征,特征是否具有代表性及特征计算的准确性均可能影响算法性能。而基于DTW-KNN可以直接依赖于呼吸波形的原始数据,无须提取特征或设置复杂的阈值。研究结果表明,较基于规则的方法及RF和AdaBoost方法相比,基于DTW-KNN的IEE检测方法在准确率上有一定优势。 DTW-KNN方法也存在以下不足:首先,KNN方法对K值比较敏感,使用KNN方法时也需要对K值进行小范围阈值的扫描,消耗一定时间;其次,呼吸气道压波形数据也包含一定的IEE特征。但是本实验只使用了IEE特征表现更明显的流速波形数据,未使用气道压特征。在后续研究中,可针对上述不足之处进行优化,以进一步提升本研究提出的IEE检测算法的性能。2 实验结果与分析
3 结 语
