量化敏感度的个性化数据发布模型
2022-09-06朱理奥曹天杰
朱理奥 曹天杰
(中国矿业大学计算机科学与技术学院 江苏 徐州 221116)
0 引 言
现如今,大数据已经成为时代热点。人们在日常生活中的方方面面享受着大数据所带来的便利。这是因为针对大数据的挖掘、分析和利用能够更好地在商业、行政决策以及科学研究领域对人们提供帮助。但是由于这些数据本身来源于现实中的每个个体,它们本身包含有大量的可以与个人产生关联的信息,甚至会包括个人所不愿意对外界披露的隐私信息。这些信息在遭到泄露之后可能会对相关联的个人产生难以预计的后果。因此,在发布大量数据的同时保证个人隐私的技术,即数据发布隐私保护技术(Privacy Preserving in Data Publishing, PPDP)[1-2]便成为了研究的重点。这些研究的重点在于如何在保证大量数据能够被用于大数据分析和利用的同时,保证用户隐私不被泄露。
最开始,人们提出的数据发布模型是建立在匿名化[3]基础上的。所谓匿名化,是指在数据发布阶段,通过一定的处理,将所发布数据与个体身份的关联打破,从而避免攻击者利用所发布出来的数据准确确定个人。这些经典的模型包括k-匿名模型[4-5](k-Anonymity)、l-多样性[6](l-Diversity)和t-近似[7](t-Closeness)等等。在这些经典的模型的基础上,有很多改进的模型被提出。不过,这些传统模型只是单纯考虑了包含隐私的数据的敏感程度。对于这一敏感程度的把握往往都是根据数据发布者基于自身经验决定,并未考虑到用户个人对于隐私保护的需求,同时也带来了可能的保护程度与实际所需不匹配的情况(即对于较不敏感的数据进行过度保护,对敏感程度较高的数据保护程度不足)。
当前,关于考虑用户自身需求的隐私保护模型,已经得到了一些关注。其中有针对每一条记录设计不同保护需求的方法[8-9],也有将个人需求作为评估标准之一的方法[10],以及为敏感属性设置泛化树的方法[11]。但是,针对保护程度与实际所需不匹配的问题却并未得到重视。仅有文献[12]提出的将敏感度量化计算的(w,l,k)-匿名模型。但是这一模型并未考虑用户个人的隐私需求。目前尚未有研究同时解决这两个问题。
本文针对数据发布中的隐私保护问题,基于(w,l,k)-匿名模型进行改进。在保留原本的利用量化计算来解决保护程度与实际所需不匹配的问题的基础上,对用户的隐私保护需求进行量化,参与敏感度的计算。本文的模型既保留了(w,l,k)-匿名模型的优势,又具有了对用户个性化隐私需求的支持,具有更好的隐私保护能力。
1 相关概念
本文在之后的讨论中将会用到一些概念,现将对这些概念进行必要的说明。
在一个数据表中,每一条数据记录(被称为元组)的各个属性可以简单划分为能够直接标识个体身份的标识符属性、组合起来可以推断用户身份的准标识符属性、敏感属性和非敏感属性。研究中,一般假定数据表中不包含标识符属性和非敏感属性,主要针对敏感属性进行隐私保护。
在讨论数据发布匿名规则时,有以下一些常用定义。
1) 等价类(Equivalence Class, EC):经过匿名化处理后,所有拥有相同准标识符属性值的元组构成一个等价类。
2)k-匿名:数据表T包含n个等价类{A1,A2,…,An}。对于T中的任意一个等价类Ai,都有:
|Ai|≥k
成立。那么则称T满足k-匿名。其中|Ai|表示等价类Ai中所包含的元组个数。
3)l-多样性:数据表T包含n个等价类{A1,A2,…,An}。对于T中的任意一个等价类Ai,其包含的敏感属性值至少有l个不同的取值,那么则称T满足l-多样性。
在对数据表应用数据发布模型时,有以下几个常用概念。
1) 泛化:指使用更具概括性意义的属性值来对具体属性值进行替代的过程。
2) 泛化树:又叫泛化层次,指表示属性值以及泛化后的属性值之间的关联的树结构。
图1是针对一个数据表中“Disease”属性的属性值所建立的一个泛化树。
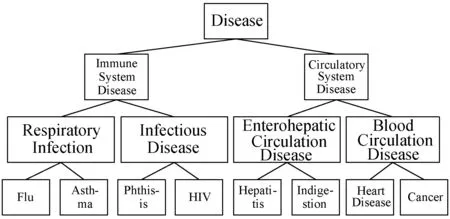
图1 “Disease”属性泛化树
2 敏感度量化模型
本节将对现有的敏感度量化模型,即(w,l,k)-匿名模型进行分析,研究其所存在的不足,并且针对这些问题提出改进模型,同时给出改进后模型的实现方式。
2.1 (w,l,k)-匿名模型
文献[12]针对数据发布模型中存在的隐私保护程度和实际所需保护不匹配的问题,提出了一个通过量化敏感度值来帮助进行数据匿名化的模型——(w,l,k)-匿名模型。
定义1((w,l,k)-匿名模型[12]) 当一个给定数据表T满足k-匿名、l-多样性,并且每个等价类的平均敏感度不超过w时,该数据表满足(w,l,k)-匿名模型。
在这个模型中,等价类M的平均敏感度waverage的计算方法被定义为:
式中:wa表示敏感属性A的某一属性值a的敏感度。它的计算方法定义为:
wa=α×wfa+(1-α)×wlaα∈[0,1]
式中:α为用于控制敏感度对于频率敏感度wfa和分级敏感度wla的依赖程度的全局参数,由数据发布者根据实际需要决定。wfa、wla的计算公式分别为:
式中:m表示A的属性值按照敏感程度划分的总等级数,fa表示属性值a在整个数据表中的频率,i表示该a所处于的敏感程度等级。
(w,l,k)-匿名模型一方面通过综合考虑敏感属性值的频率敏感度和分级敏感度,避免了发布者完全凭借自身经验决定隐私保护程度所带来的主观性过强的问题,另一方面利用量化计算来帮助发布者判断具体所需要的隐私保护程度。但是,该模型仅仅考虑了敏感属性值本身的敏感程度,并未考虑到用户个人对于隐私保护的需求。在某些情况下,用户可能会出于自身的特殊情况,对较低敏感度的敏感属性提出较高的隐私保护需求。在这种情形下,这一模型便不再适用。
2.2 个性化(w,l,k)-匿名模型
根据上文提及到的(w,l,k)-匿名模型所存在的问题,本文针对性地提出个性化-(w,l,k)-匿名模型。在原本模型的基础上,将用户个人的隐私需求进行量化,参与到等价类的平均敏感程度的计算当中。
对于用户的隐私需求,参考敏感属性值的语义敏感度分级方法,考虑设立如表1所示的一个用户隐私需求等级表。
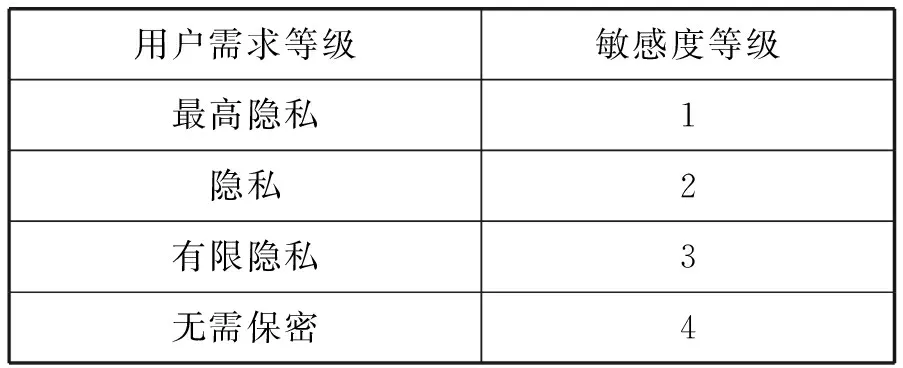
表1 用户隐私需求等级表示例
设立用户隐私需求等级表的目的在于,实际情况下,用户本身仅仅能够对自己的隐私需求有一个感性认知,而并不能直接提供一个定量数据。此外,这也便于在实际应用情形下,通过发放调查问卷的方法向用户搜集其个性化隐私需求。
在此基础上,给每个需求等级赋一个表征敏感度的数值,以便进行量化。数值越大,表示所要求的保护等级越高。表2便是针对表1的一个量化示例。

表2 对表1的量化示例
在完成了对用户需求的量化定义之后,便可以进一步定义用户隐私需求的计算方法。
定义2(用户需求敏感度计算方法) 根据用户对于隐私保护程度需求在泛化层次树上对应的层级ipl,可以计算出用户需求敏感度wapl:
定义3(敏感属性值综合敏感度计算) 考虑用户敏感度需求的某一敏感属性A的属性值a的综合敏感度wgeneral的计算方法如下:
wgeneral=max{α×wfa+(1-α)×wla,wapl}α∈[0,1]
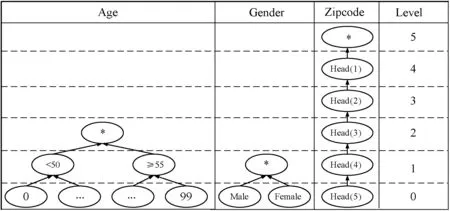
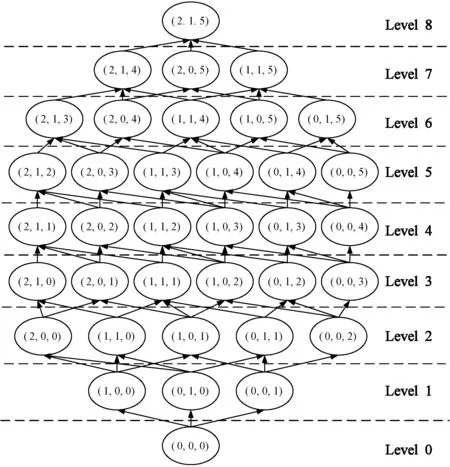
如果α×wfa+(1-α)×wla≥wapl,此时用户需求wapl低于属性值敏感度权重wa,取wa作为最终的综合敏感度;如果α×wfa+(1-α)×wla 在定义了用户的隐私需求计算方法之后,可以给出改进模型的定义。 定义4(个性化(w,l,k)-匿名模型) 当一个给定数据表T满足k-匿名、l-多样性,并且每个等价类的平均综合敏感度不超过w时,该数据表满足要求个性化(w,l,k)-匿名模型。 其中,某个等价类M的平均综合敏感度wgeneral_average的计算方法为: 模型中依然保留有参数α,由数据发布者根据实际情况,决定在计算属性值敏感度权重时对语义敏感度和频率敏感度的倚重程度。 k-匿名的要求是为了防止数据表经过匿名处理后,由于等价类中可能仅仅含有一条记录而导致隐私泄露。l-多样性的要求是为了防止由于等价类中敏感属性值取值相同而导致的隐私泄露。平均综合敏感度同时考虑到了敏感属性值的频率分布、语义敏感性以及用户自身的需求,表征了等价类中各敏感属性值在综合这三方面的普遍敏感水平。对其进行限制便是对每一个等价类的敏感水平进行限制,防止由于一个等价类中因为包含占比过大的高敏感属性值而导致的隐私泄露。 在模型的实现方面,本文将同文献[12]一样使用基于ARX框架[13]的Flash算法[14],来对个性化(w,l,k)-匿名模型进行实现。 在介绍具体实现算法之前,首先需要介绍在该算法中所使用的泛化格的概念。 定义5(泛化格) 将数据表中每个属性的泛化程度用泛化层次高度进行表示,可以得到一个表示针对当前数据表的泛化配置的数字列表。所有的这些列表所表示的泛化配置空间,被称为泛化格。 例如,由图2所示的泛化层次,其对应的泛化格如图3所示。 图2 三个属性的泛化层次 图3 由图2所产生的泛化格 泛化格通过将泛化配置简化为一个数字组成的列表,从而简洁方便地将针对一个特定数据表的泛化空间表示为树的形式,为存储和遍历泛化空间提供了便利。 Flash算法通过对于泛化格的自下而上的二分查找,遍历泛化格的所有节点,以便寻找到满足匿名化方案的最优解。由于ARX框架本身对于数据表进行了大量优化,利用哈希表、快照缓冲区等方法提高了对于匿名状态的检查速度,对泛化格的遍历搜索和检查成为可能。 算法1Flash算法外循环 输入:Laticelattice //输入泛化格 开始 heap=newmin-heap //最小堆 for/from0tolattice.height-1do foreachnode∈level[l]do if!node.taggedthen path=FINDPATH(node) CHECKPATH(path,heap) while!heap.isEmptydo node=heap.extractMin foreachup∈node.successorsdo if!up.taggedthen path=FINDPATH(up) CHECKPATH(path,heap) 算法的外循环:主要是实现了针对泛化格的深度优先贪婪搜索。每次遇到未被标记为已被检查过的节点,便调用FINDPATH(NODE)方法来找到一条从NODE到顶层的路径,并且对路径调用CHECKPATH(PATH,HEAP)方法进行检查。 算法2FINDPATH(NODE) 输入:Start nodenode 输出:Path of untagged nodespath 开始 //寻找一条未被标记的节点组成的路径 path=new list whilepath.head() !=nodedo path.add(node) foreachup∈node.successorsdo if!up.taggedthen node=up break returnpath FINDPATH(NODE)方法:针对每一个节点,寻找它首个未被标记的子节点加入路径,直到抵达泛化格最顶端或是当前节点的所有子节点已被标记时停止。返回路径,以便对路径中的节点进行检查。 算法3CHECKPATH(PATH,HEAP) 输入:Pathpath, heapheap 开始 Low=0;high=path.size-1;optmum=null whilelow≤highdo mid=int((low+high)/2) //向下取整 node=path.get(mid) //选取中间节点进行二分搜索 ifCHECKANDTAG(NODE)then //CHECKANDTAG //(NODE)将检查节点的匿名性,并且标记已被检查过的节点 //当前节点符合匿名条件 optimum=node high=mid-1 else //当前节点不符合匿名条件 heap.add(node) low=mid+1 STORE(optimum) //存储符合匿名条件的节点的局部最优 //解,因为它可能是全局最优解 检查路径的方法。对路径进行二分搜索。对每一个节点调用CHECKANDTAG(NODE)方法进行匿名性检查,判断该节点所代表的泛化配置是否满足匿名模型的要求。如果满足,则将其储存;如果不满足,则不储存。由于ARX框架本身进行了针对性优化,将数据表中的各个属性值(包括泛化后的所有可能的值)转化为数值,并且以哈希表的形式进行存储。每次判断匿名条件是否符合时,仅仅对受到泛化配置改变影响的部分进行修改,保留不受影响的部分,算法运行耗时较短。 将通过实验来对本文模型和(w,l,k)-匿名模型进行比较,以便对本文模型的性能进行评估。 在评价本文提出的数据发布模型时,将从数据效用和隐私保护两个方面进行评估。 在评价数据效用方面,将采用AECS和PM作为评估指标。 定义6(平均等价类大小[15],Average Equivalence Class Size,AECS) 数据表T中等价类的平均大小。 式中:|T|表示数据表中的总元组个数;k为k-匿名模型的参数;total_equivalence_class表示等价类的总个数。 定义7(准确度[5],Precision Metric,PM)一个表征数据表T中属性A的各属性值Ai泛化所带来的损失的量。 式中:NA表示表中属性的个数;N表示表中元组的个数;|DGHAi|表示属性Ai的泛化层次总高度;h表示当前泛化方法下单个属性值的泛化高度。 在评估隐私保护时,将与文献[12]相同,使用高危等价类占比(即高危等价类占总等价类的比例)作为评估指标。 定义8(高危等价类[12]) 如果一个等价类M中具有最高敏感等级的属性值在该等价类中的频率之和是其在整个数据表中的频率的5倍或以上,那么该等价类M是一个高危等价类。 一般而言,高危等价类占比越高,属性值披露风险越大。 在数据选用方面,使用相关研究中被广为使用的Adult数据集。这个数据集来自UCI Machine Learning Repository,是一个公开数据集。它包括了48 842条数据记录。在删除其中的拥有空值和不确定值得记录之后,最终得到30 169条数据。为方便计算,随机选取其中的30 000条数据作为实验用数据集。与相关研究的各文献一样,选取{Age, Work-class, Education, Native-Country, Marital Status, Race, Sex}这几项作为准标识符属性。由于原数据集中并未包含敏感数据属性,现为各数据项按照如表1所示的频率,随机地分配Disease数据项的各属性值,并且由此可以计算出相应的频率敏感度wfa。 表3 Disease数据项的各属性值及其相应的频率敏感度wfa 这些属性值的敏感度分级以及每个属性值相对应的分级敏感度如表4所示。 表4 Disease数据项的各属性值的敏感度分级及其相应的分级敏感度wla 实验中,为每条记录随机生成一个用户隐私需求等级。其具体的分级如表5所示。 表5 用户个人隐私需求等级及其相应的敏感度wapl 实验中取参数α=0.5,l=4。实验使用的CPU为Intel Core i7- 8750H,操作系统为Windows 10,编程语言为Java。实验中选取AECS和PM作为数据效用的度量,使用高位等价类占比作为隐私保护程度的度量。由于实验中整张表格的敏感度值的平均数为0.567,w的取值如果低于这个值可能会导致过多的数据效用损失。因此,实验中取w=0.65。实验将本文模型与改进前的模型进行比较。 随着k的取值的增大,两种模型的平均等价类大小都在减小。这是因为AECS的计算公式排除了k的取值对于等价类大小的影响。从图4中可以看到,在k≤50时,本文模型的AECS均大于(w,l,k)-匿名模型。这是因为由于本文模型在计算综合敏感度时,是选取了wa和wapl两者之间的最大值。这一步导致了对于每一个敏感属性值,必定有wgeneral≥wa。在模型参数w的取值一定的情况下,为了满足匿名要求,应用了个性化(w,l,k)-匿名模型的数据表需要在等价类中拥有更多的元组,即令等价类更大,才能满足同样的匿名要求。此外,从图4中同样可以看出,在k=100时,两个模型的AECS大小相等,并且在之后保持了相等的状态。这表明随着k的取值的增大,k逐渐取代匿名模型,成为了对于数据效用的主要影响因素。 图4 AECS与k的取值关系 如图5所示,PM呈现出了相同的趋势,随着k值的增大而减小。这是由于随着k值的增大,等价类的总体大小在增大,在进行数据匿名化时需要对准标识符所包含的信息进行更大程度的抹除,消除每个元组的独特性,才能让更多的元组出于同一等价类中。(w,l,k)-匿名模型在k≤50时,具有相对于本文模型的更高的PM,但优势很小,PM差值不足0.05,并且在k=100时被个性化(w,l,k)-匿名模型追平。正如文献[16]所指出的,寻找一个拥有最高数据效用同时具有最优隐私保护能力的k-匿名数据集是一个NP难问题。由于本文方案提出了更高的隐私保护要求,在数据效用方面会有所牺牲。 图5 PM与k的取值关系 在隐私保护方面的情况如图6所示。 图6 高危等价类占比与k的取值关系 随着k值的增大,无论模型选择,高危等价类占比都在减小。这是因为针对一个特定数据集,数据总量是一定的。等价类的增大将会导致等价类总数的减小,这将导致等价类中的各属性值的分布逐渐接近于其在整张数据表中的分布。最终,当数据表内所有元组都被划归为一个等价类时,等价类中的属性值分布将与在数据表中的分布一致。在k≤50时,本文模型始终具有更低的高危等价类占比。这是因为本文模型具有平均大小更大的等价类,这使得敏感属性值的分布相比于(w,l,k)-匿名模型更接近于数据表内的分布。当k≥100时,两个模型均不包含高危等价类。 综合以上分析,可以得出结论:个性化(w,l,k)-匿名模型相比较于(w,l,k)-匿名模型,在实现了对用户隐私的个性化保护的同时,牺牲了一定的数据效用,但具有更高的隐私保护能力。 本文针对现有的数据发布模型中存在的问题,在继承了量化计算敏感程度的思路的情况下,对(w,l,k)-匿名模型进行了改进,得到了一个能够考虑用户自身隐私需求的数据发布模型。该模型在让数据满足k-匿名和l-多样性的前提下,通过量化用户隐私需求,并将其参与敏感度计算的方法,使得最终的等价类划分能够体现用户的个性化需求。经过实验证明,本文模型在牺牲了一定的数据效用的情况下,能够有效地个性化地保护用户隐私,并且具有更好的隐私保护能力。 目前考虑用户隐私需求的模型大部分单纯依赖用户指定来确定用户需求,这一过程存在较大主观性。用户有可能会高估自身信息所需要的保密等级,而这会导致毫无必要的数据效用损失。一种能够客观评估用户个性化需求是否合理的方法将在未来的研究中进行探讨。2.3 模型实现
3 实 验
3.1 模型评估指标
3.2 评估实验设计
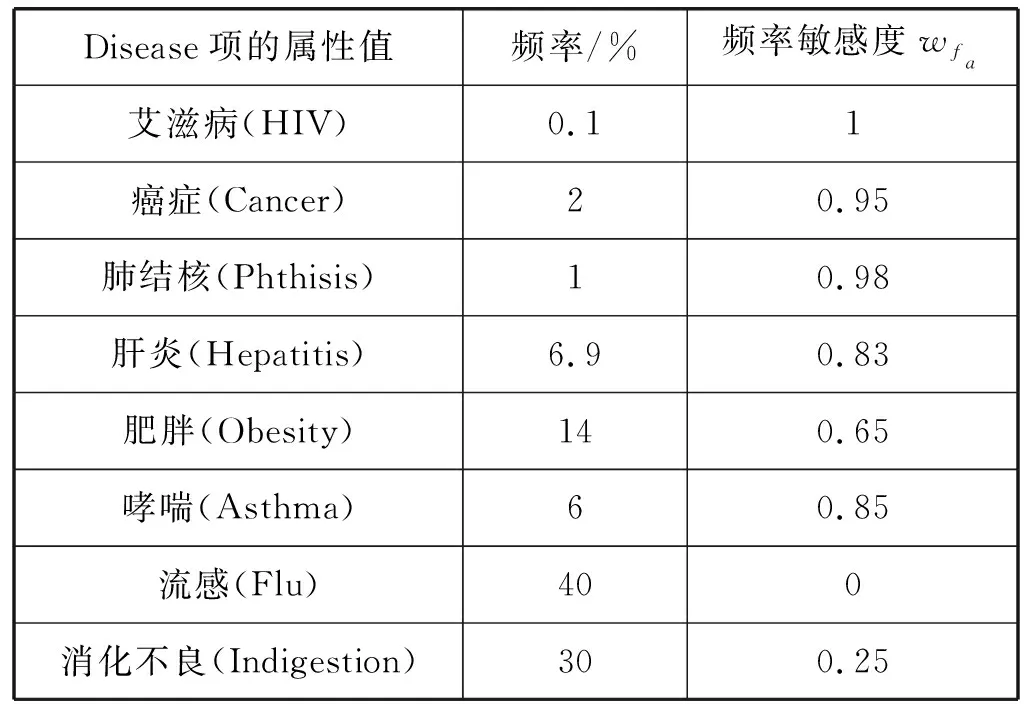


3.3 实验结果
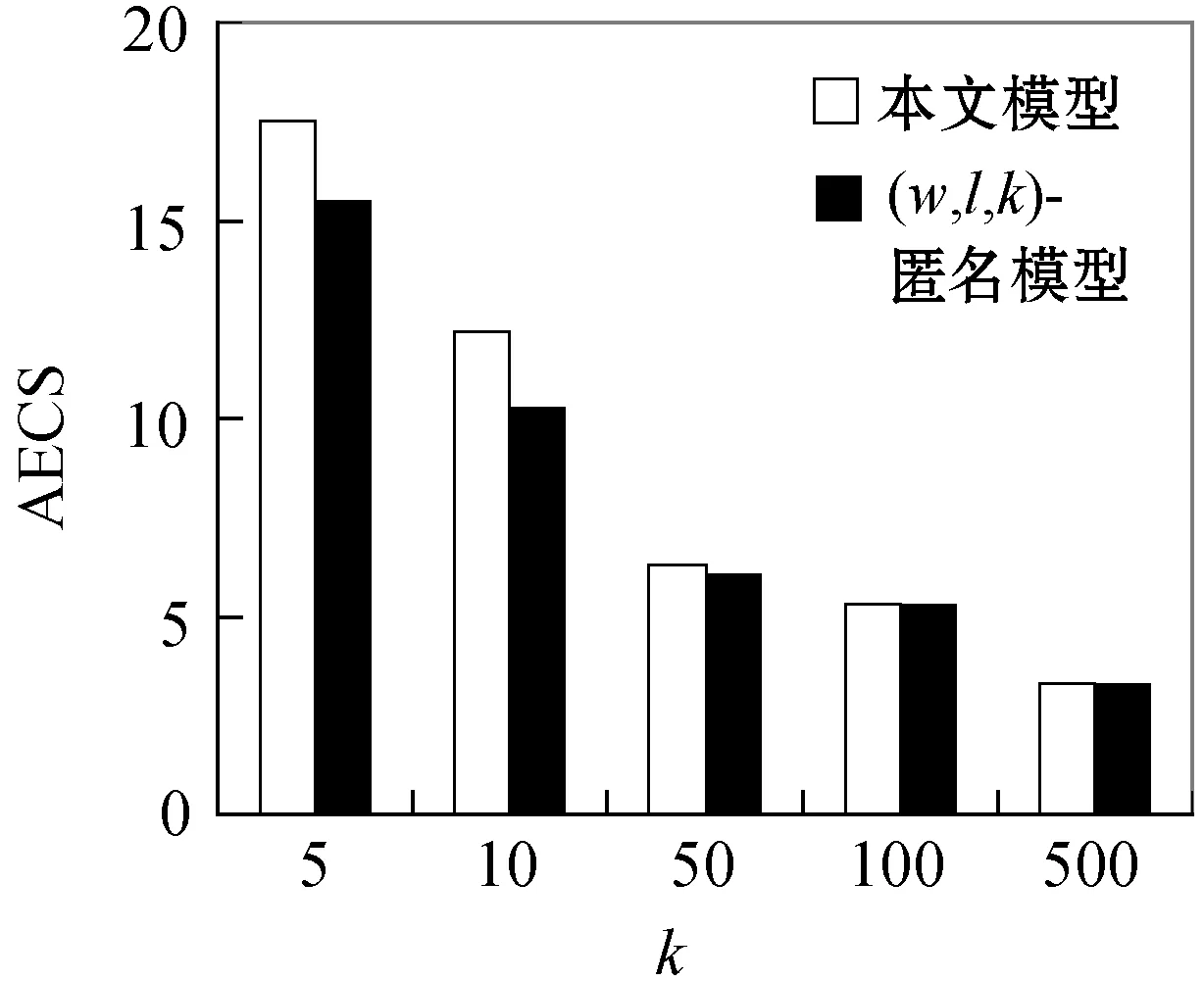


4 结 语
