软黏土地基中吸力桩水平承载性能数值分析

张 伟，马振杰

(天津大学 建筑工程学院，天津 300350)

近年来，随着深海油气开采的逐渐发展，传统的重力式基础和桩基导管架平台已很难适应深海施工需求，在此情况下，立柱式平台、浮式平台等新型结构及基础逐渐得到应用。作为一种深海新型桩基础，吸力桩安装过程为：吸力桩借助自重作用沉至海底，然后通过抽气孔利用真空气泵在桶内形成负压，桶内外的压力差将吸力桩压入土体。当需要移除吸力桩时，只需要向桶内充气将吸力桩拔出即可。因此，吸力桩具有方便施工、可重复使用等优点。

目前对吸力桩的研究，主要从现场试验、离心机试验、实验室试验和数值仿真两方面开展，现场试验测量数据较为真实可靠，但时间和经济成本较高[1-5]。近年来，许多学者利用ABAQUS[6]、FLAC3D[7]、Z_SOIL[8]等大型有限元软件对吸力桩的结构参数等展开了全面广泛的研究。在传统吸力桩的基础上，李大勇等[9-12]提出了一种新型裙式吸力基础，并通过模型试验和有限元软件对吸力桩基础的承载特性、沉贯特性等展开了深入研究。在李大勇提出的裙式吸力基础上，柳晓科等[13-14]提出了低裙式吸力桩基础，并通过模型试验和PLAXIS有限元软件对其真空沉贯特性和抗拔特性进行了研究。

本文通过有限元软件ABAQUS来模拟不同裙尺寸的吸力桩的水平承载特性，对吸力桩基础展开进一步研究，分析裙结构对吸力桩的水平承载特性，并采用极限平衡法对吸力桩水平极限承载力进行理论推导。

1 吸力桩基础分析模型

基于ABAQUS三维有限元软件，根据文献[15]数据建立三维有限元计算模型。吸力桩外径D=5 m，长径比分别为L/D=1.0、2.0、5.0，桶壁厚50 mm，承台厚100 mm。考虑到边界效应，土体在纵向和横向的计算范围取为6L和10D。考虑到吸力桩结构的对称性，取吸力桩结构和与计算区域的一半建立有限元计算模型。吸力桩周围土体为软黏土，采用基于Mohr-Coulomb屈服准则的理想弹塑性模型，泊松比v=0.49，即假定土体不可压缩，土体容重γ=18 kN/m3，不排水抗剪强度cu取10 kPa，摩擦角φ=0，不考虑地基中应力对土体模量的影响，假定土体模量与土体不排水抗剪强度成正比，即E=500cu。考虑到吸力桩的刚度远远大于海洋土地基的刚度，因此将吸力桩简化为弹性材料，弹性模量为E=2×105MPa，泊松比取0.3。为便于收敛，将吸力桩密度设置为土体密度。有限元计算模型及模型简图如图1和图2所示。

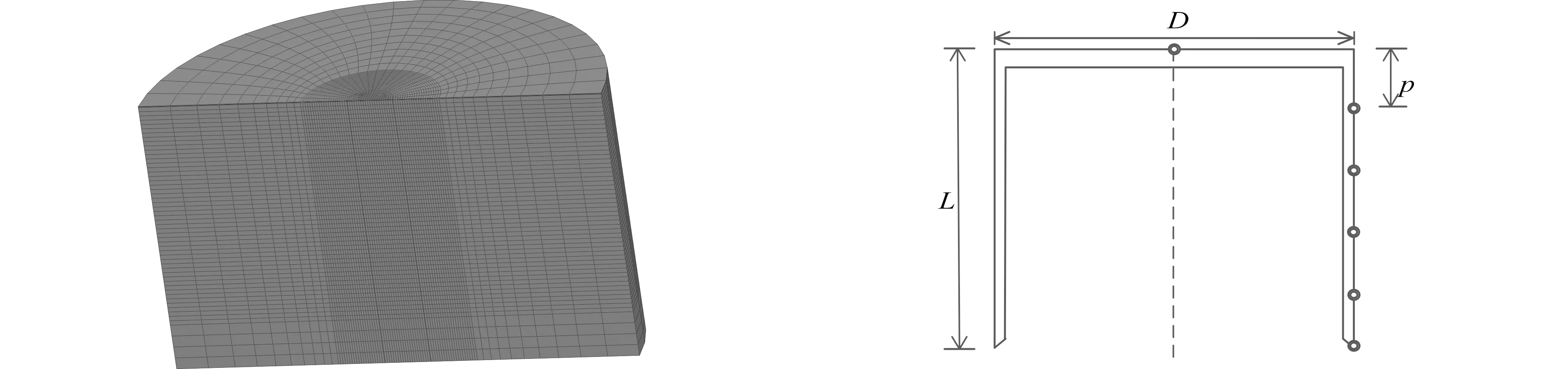
图1 三维有限元计算模型

对于吸力桩和土体，均采用C3D8单元建立有限元计算模型。吸力桩与土体之间设置接触面，接触面法向为硬接触，切向为Penalty接触。计算时假定吸力桩已贯入土体，桩底部与土体接触面为水平。除初始分析步外，另设两个分析步，第一步生成初始应力场；第二步采用位移控制方法进行水平位移的加载。

在桩顶位置采用位移控制方法施加水平位移，加载点的荷载-位移曲线如图3所示，其加载过程可分为三个阶段。在第三阶段，荷载-位移关系曲线，荷载不再随位移增大而增大，土体失稳，此阶段的荷载值可作为吸力桩的水平承载力。

图3 吸力桩水平位移-荷载关系曲线

在加载点位置p/L=0、0.2、0.4、0.6、0.8、1.0处分别施加位移，并将得到的水平承载力进行归一化处理，得到不同长径比下水平承载力随加载点位置变化的关系如图4所示，其中Hmax为最大水平承载力。图5给出了p/L分别为0、0.6、1.0时吸力桩的水平破坏机制。通过对比发现，本文数据与文献有限元分析数据差值大部分在10%以内，水平破坏机制近似，即所得结论相同，证明本文数值模型可有效模拟吸力桩的水平受荷过程。

5-a p/L=0，文献数据 5-b p/L=0.6，文献数据 5-c p/L=1.0，文献数据

裙式及低裙式吸力桩模型简图如图6所示，去掉裙结构后，即为传统吸力桩；当裙顶与主桶顶部高差t为0时，即为裙式吸力桩基础；当t不为0时，即为低裙式吸力桩。图中L为主桶高度，取为25 m；D为主桶直径，取5 m；m为裙宽，p为加载点位置与主桶顶部之间的距离。h为裙高，本文规定当h/L=0时表示只有裙结构承台，无裙壁。

图6 裙式吸力桩模型简图

不同尺寸的吸力桩基础结构模型如表1所示。

表1 吸力桩尺寸表

2 数值计算结果分析

2.1 加载点位置对水平承载力的影响

针对传统吸力桩模型，采用控制位移法，在p/L=0、0.2、0.4、0.6、0.8、1.0的位置施加水平位移，得到不同加载点位置下的水平位移-荷载曲线如图7所示。由图可以发现，当p/L=0.6时，吸力桩基础极限承载力最大，p/L=0.4、0.8时的水平极限承载力接近，p/L=0.2、1.0时的水平极限承载力接近。

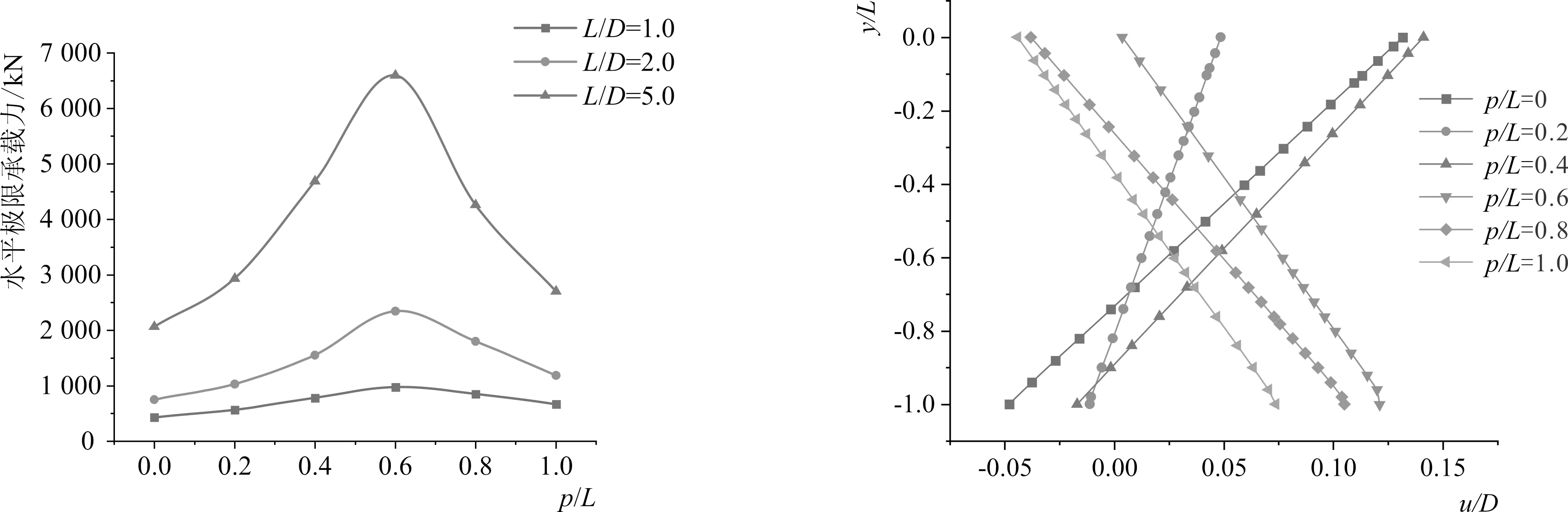
图7 加载点位置对水平极限承载力的影响

根据已有研究显示[16]，在水平受荷过程中，通常是加载反方向的吸力桩周围被动区土体屈服，进而导致吸力桩失稳，吸力桩周围被动区越大，则吸力桩越不容易失稳，其水平极限承载能力越大。通过分析吸力桩失稳时沿埋深方向中心线上各点的侧移，得到侧移量为0的点，认为该点为吸力桩基础的转动中心，进一步确定桩体周围被动区的大小。图8为传统吸力桩基础在水平荷载下的侧移-埋深曲线，其中y为沿桩体埋深，u为某点的侧移，负值代表沿加载反方向产生侧移，正值代表沿加载方向产生侧移。由图可以看出，当p/L=0.6时，转动中心位置接近于地面，此时桩体后侧被动区域最大，水平极限承载能力也为最大。当p/L分别为0.4、0.8时，桩体转动中心分别处于0.9、0.25附近，与桩底、桩顶的距离相接近，水平极限荷载相接近。

2.2 裙结构对水平承载力的影响

图9显示了不同加载点位置下裙结构对水平极限承载力的影响。当加载点位置p/L=0、0.2、0.4时，随着裙宽和裙高的增长，水平极限承载力以近似线性的关系增长，而随着高差的增大，水平极限承载力有较小增长而后趋于不变。当加载点位置p/L=0.6、0.8、1.0时，裙结构对水平极限承载力的影响较小。

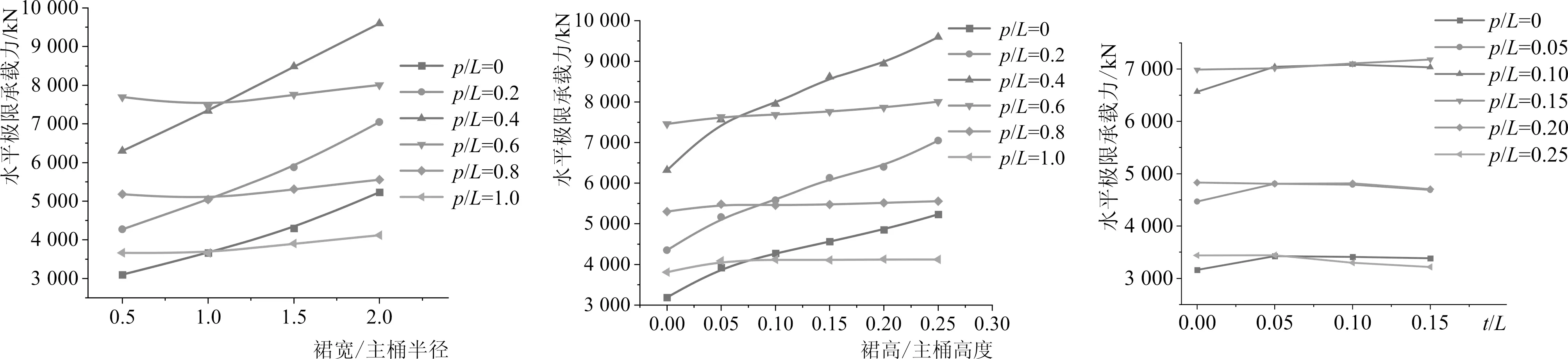
9-a h/L=0.25，t/L=0 9-b m/R=2，t/L=0 9-c m/R=1.0，h/L=0.15

图10显示了p/L=0时水平荷载作用下不同类型吸力桩基础的破坏机理，传统吸力桩在绕桩身某点转动过程中受到桩侧水平土抗力和桩端摩阻力的作用。相较于传统吸力桩基础，裙结构的设置增大了吸力桩与土体的接触面积，使得吸力桩还受到裙端摩阻力和裙前水平土抗力的作用。随着裙结构的下移，裙顶与土体相接触，使得吸力桩在裙式吸力桩的基础上还受到裙顶摩阻力的作用。当裙结构继续下移，由于吸力桩与土体接触面积未增加，水平极限承载力不再增长。

10-a 传统吸力桩 10-b 裙式吸力桩 10-c 低裙式吸力桩

由图8可以看出，当加载点位置处于p/L=0、0.2、0.4时，桩身上部位移较大，而当加载点位置p/L=0.6、0.8、1.0时，桩身下部位移较大。由于裙结构主要设置在靠近桩顶位置，因此当位移主要集中在下部时，裙结构对水平承载性能的影响较小。

3 吸力桩基础水平承载力理论计算

采用极限平衡法对吸力桩水平极限承载力进行理论分析，过程中存在以下假设：桩头不受转动约束，能够自由转动；不考虑桩的倾斜对水平承载力的影响；桩内土体与桩体共同运动，不考虑吸力的影响。在水平受荷过程中，桩体绕桩身某一点转动，主要受到桩前土压力、桩底摩阻力、桩底反力和桩外侧摩阻力的作用，其中桩前土压力包括旋转中心以上的桩前土压力和旋转中心以下的桩后土压力，受力示意如图11所示。

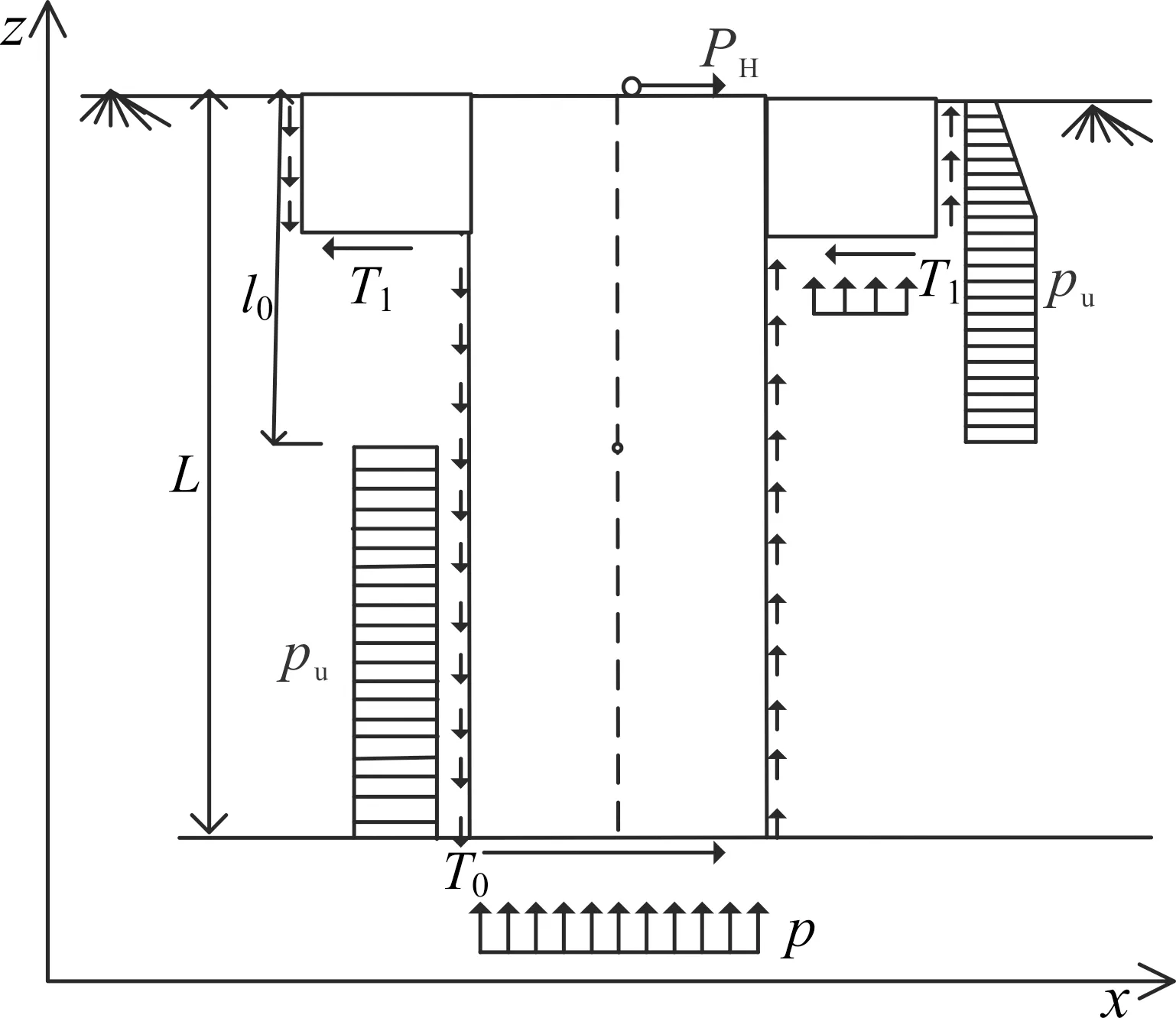
图11 水平荷载作用下吸力桩受力示意图

通过将桩体(包括桩内土体)所受力系对水平方向进行受力平衡分析，可得到桩体水平极限承载力如下

(1)

式中：T0=πR2cu，为桩底摩阻力，kN；T1=T2=π[(R+m)2-R2]cu，为裙端、裙顶摩阻力，T2只存在于低裙式吸力桩情形下；当处于主桶部位时取M=D，当处于裙结构部位时取M=D+2m；l0为桩体旋转中心至桩顶距离，m，可通过将力系对水平荷载作用点取矩进行力矩平衡分析求得；pu(z)为深度z处的土抗力，kN/m2，采用Matlock法来确定，认为土抗力可按式(2)与式(3)计算，并取其中的较小值作为土抗力。

pu(z)=9cu

(2)

(3)

式中：γ为土体重度，kN/m3；J为试验系数，对于软粘土取0.5。

理论结果与有限元计算结果对比如表2所示。可以看出，理论结果与有限元结果相差较小，契合度较高。

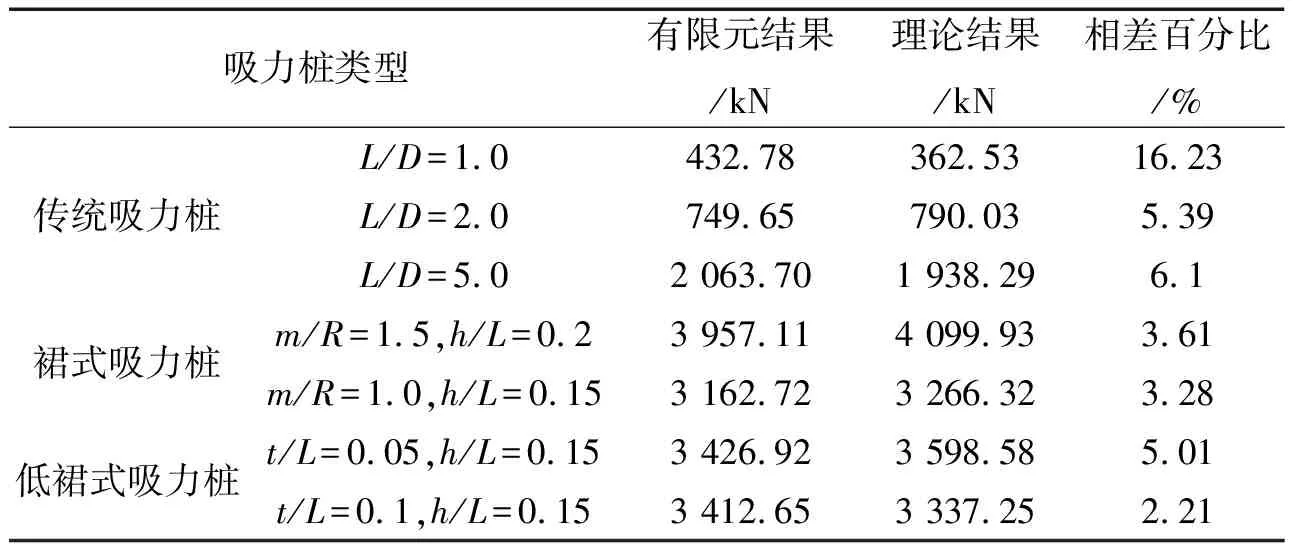
表2 有限元结果与理论计算结果对比

4 结论

本文对饱和软黏土中不同裙结构的吸力桩的水平承载性能展开了详细研究，结论如下：

(1)在水平荷载作用下，吸力桩绕桩身某点转动，在转动过程中受到桩前土抗力、桩端摩阻力的作用，裙式吸力桩还受到裙前土抗力、裙端摩阻力的作用，当裙结构下移之后还会受到桩顶摩阻力的作用。(2)加载点位置的变化，引起了转动中心的变化，由于主要是桩前土抗力抵抗桩体转动，所以当加载点位置p/L=0.6时，转动中心靠近桩顶，此时桩前土抗力最大，水平极限承载力最大。(3)裙结构的设置主要增大了桩体与土体的接触面积，裙高和裙宽对水平极限承载力的影响近似线性，而当裙顶与土体接触以后，裙结构的下移不再对承载性能有影响。(4)基于极限平衡法对吸力桩水平极限承载力进行了理论计算，对比结果显示该式能够用来计算不同裙结构的吸力桩水平极限承载力。