压电悬臂梁驱动传感共位特性研究

伍 德， 彭来湖，2*

(1.浙江理工大学 浙江省现代纺织装备技术重点实验室， 浙江 杭州 310018；2.杭州勤诚微电子科技有限公司， 浙江 杭州 310018)

压电陶瓷其特殊性在于它可以实现机械能与电能之间的相互转化，广泛用于结构振动控制[1]、结构健康检测[2-3]、选针器的驱动机构[4]、悬臂梁式压电风能发电装置[5]、压电振子[6]和医疗微型压电驱动系统[7]等微小驱动元件领域。1993年，由Sincarsin等[8]成功将传感器与驱动器集成一体并将其命名为“传感驱动器”。1995年钱新恩[9]利用简单搭建的试验平台，实现了单块压电材料的传感功能和执行功能。2011年张忠华等[10]通过改变压电堆叠的边界条件总结得到驱动器位移量的变化规律。2015年刘艳梅等[11]对实际压电陶瓷驱动特性进行测量，得到了与理论一致的压电陶瓷驱动特性曲线。2018年哈尔滨工业大学的董欣[12]在结构上集成了压电传感驱动器，推导得到驱动器与传感器的数学模型，He等[13]建立压电堆叠的机电耦合模型以及电机主轴的动力学模型。2019年陆颢瓒等[14]建立了单压电悬臂梁能量收集器在振动激励下的力学模型以及压电输出模型。Pelletier[15]考虑到压电驱动器在振动中会引起局部应变，提出了一种补偿方法，为采集共位信号提供了方法。王光庆[16]基于压电双向效应，借助ANSYS软件建立了压电振子有限元模型，为本研究进行有限元仿真提供了思路。

通过以上文献可知，驱动传感器的成功研制为驱动传感共位特性研究奠定了基础。但现有研究大部分着重于压电陶瓷功能性研究，主要用于结构主动抑制振动、结构健康检测及医疗微型驱动等领域。在同时实现驱动和传感的功能前提下，并未对驱动传感功能共位时内部电流信号的特性进行研究分析。

课题组对压电陶瓷驱动传感共位特性进行探究，通过理论推导验证了压电悬臂梁分别作为传感器、驱动器、传感驱动器工作时内部电流的变化规律，揭示驱动传感信号共位的特性；最后通过仿真和实验验证在不同工作条件下其共位信号的特点，以期为压电陶瓷驱动传感共位特性在微小驱动元件等领域的研究提供参考，对利用共位检测信号的压电结构自检测方面研究具有一定意义。

1 双晶片压电悬臂梁共位工作机理

压电悬臂梁是压电材料在工程中最常用的机械结构，一般为单层或双层压电晶片与一基板组成的耦合体，如图1(a)和(b)所示；借此耦合体实现传感或执行功能以满足工程上的需求。无论单层晶体还是双层晶体的压电悬臂梁，在绝大多数情况下仅应用其传感或执行功能中的一种，并未将其作为传感驱动器来用。现研究人员将传感驱动器分成结构集成型和功能集成型，如图1(c)和(d)所示。分类依据为传感器和驱动器的集成方式，其主要区别在于2个功能是否由1个器件来承担实现。集成型压电传感器分别由2个独立的器件来承担，将驱动器和传感器在结构上集成在一起；而功能型的传感器则由1个器件来实现传感和执行功能。

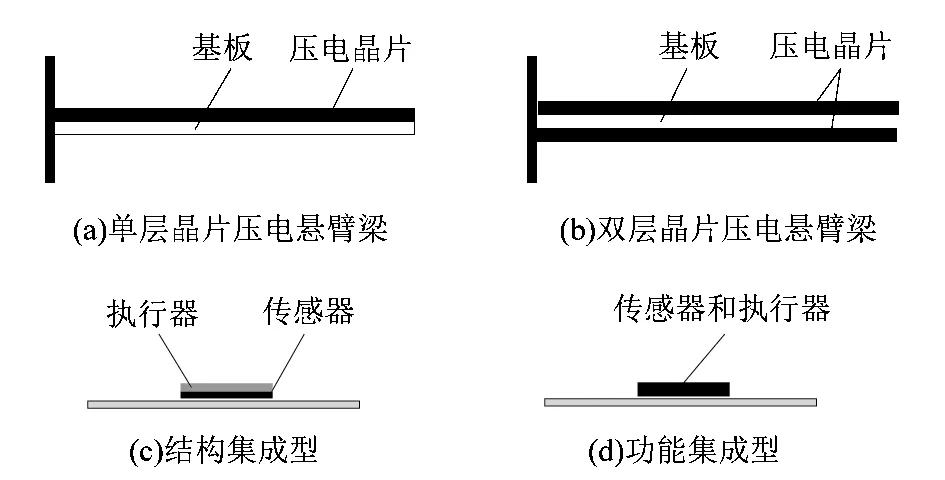
图1 压电悬臂梁类型及传感驱动器类型Figure 1 Piezoelectric cantilever type and sensor actuator type

课题组采用双层晶片压电悬臂梁作为研究对象，其中一片实现驱动传感功能，另一片作为传感器采样信号，将2片作为对照组，以提高本研究的可靠性。在实际应用中，相较于单层压电晶片悬臂梁，其优势在于高频工作条件下可通过分时驱动上下2片压电晶片使压电悬臂梁摆动。该方法具有工作寿命长、产热低、稳定性高等特点。本次研究压电悬臂梁的边界条件为机械自由和电学短路，因采用第一类压电方程作为理论基础，取应力和电场强度为自变量，应变和电位移为因变量。则压电方程可表示为：

(1)

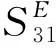
对于压电悬臂梁，当在压电晶片上施加一与极化方向相同的电场，因电场作用，使得极化强度增大，此时压电晶片内电荷之间的距离发生变化，造成压电晶片沿极化方向缩短或伸长，使得压电悬臂梁弯曲摆动，此时压电悬臂梁的等效电路内会因外加电场产生电信号。在正常弯曲摆动过程中，压电悬臂梁局部产生应变变形，二次压电效应产生电信号耦合进入内部等效电路中。若在摆动过程中与外界产生碰撞，当碰撞力或其分力方向与极化方向平行时，压电晶片受力变形，内部电荷之间距离减小，产生电位移，从而产生放电现象；当碰撞力消失，压电晶片恢复原有形状，同理会产生充电现象。根据压电悬臂梁的工作条件，以上几种信号会根据出现的时间不同耦合在一起，出现信号共位的情况。针对该共位信号的特性展开深入研究，详细解析双晶片压电悬臂梁作为传感驱动器工作时内部电流变化的特点。

2 压电悬臂梁驱动传感电流特性分析

双层压电晶片耦合体的材料为PZT-5H，极化方向沿压电悬臂梁的厚度方向。并且选用高碳纤维作为中间基板。3层结构之间通过胶粘接而成。悬臂梁固定端通过导电柱为压电悬臂梁供电。压电悬臂梁的尺寸以及实物如表1和图2所示。

表1 压电悬臂梁组成材料以及尺寸大小

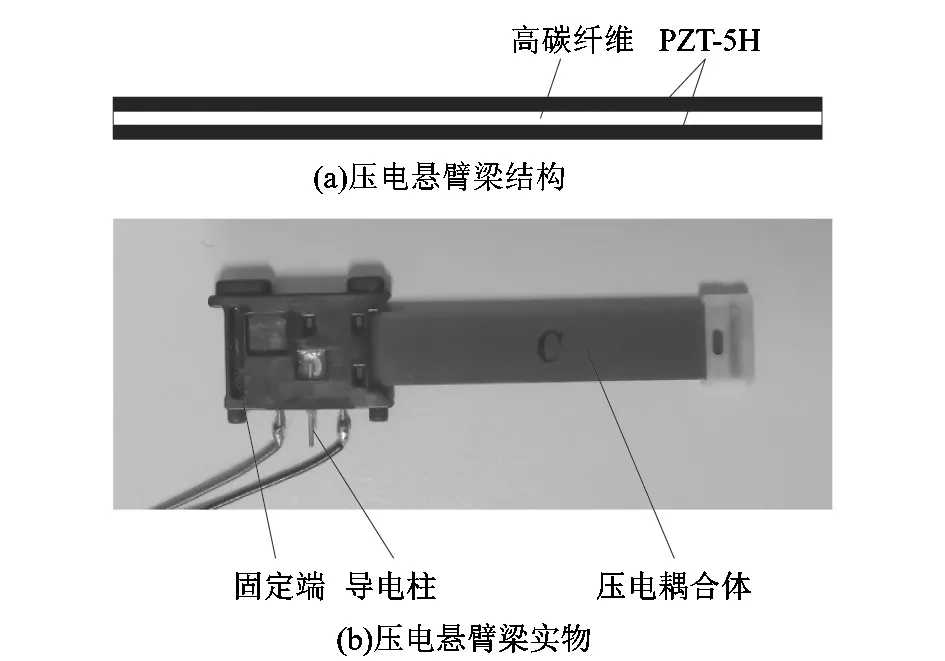
图2 压电悬臂梁结构和实物Figure 2 Schematic and physical of piezoelectric cantilever

2.1 压电驱动器电流特性

压电悬臂梁做为驱动器时，可运用机电等效的方法，根据机电类比原理将机械振动与电路振荡2个领域的问题归结到一起分析机电耦合问题。电路中常用的基本原件有电容器、电阻器和电感线圈，而机械系统中常用元件有质量元件、阻尼元件和弹性元件。将电能与机械能进行对比，具体对比关系如表2所示。

表2 机械系统与电路系统中功能关系

从表2可知，在机械系统与电路系统中，质量元件、弹性元件和阻尼元件功能分别类似于电感元件、电容元件和电阻元件。针对压电陶瓷的基频共振电路，可将其类比等效为单自由度机械振动系统。在实际工况中存在阻尼，需考虑机械损耗，因此根据压电材料基频附近的电路特性可将其等效电路简化为一电容C0并联由电容C1、电阻R1、电感L1组成电路，等效示意如图3(a)所示。由阻抗分析仪(图3(b)所示)测出其等效电路具体数值如下：电阻R1=8.863 2 kΩ，电容C1=305.7 pF，电感L1=95.378 H，电容C0=13.765 nF。

压电陶瓷片处于自由状态时，在激励电压下，其内部存在由等效电路产生的电流信号，且该电流的具体变化特征为：①在电容C0的作用下产生充放电过程;②在图3(a)等效电路的作用下会产生振荡电流。2种电流耦合在一起即为自由状态下压电陶瓷片内部电流的变化特征。借助Multisim软件搭建如图3(c)所示仿真电路，探究自由状态下压电陶瓷的内部电流变化特征。图3(d)为压电陶瓷自由状态下等效电路的充放电过程，因充放电过程中幅值相对于等效电路的幅值较大，为方便后续实验测量数据与观察分析，在采样电路中加入一放大电阻，通过检测电阻的电压值，来反映内部电流的变化。

图3 压电陶瓷片自由状态下仿真电路及电压特性Figure 3 Simulation circuit and current characteristics of piezoelectric ceramics in free state

当压电陶瓷片边界条件发生改变时，将压电陶瓷片一端作为固定约束，成为压电悬臂梁模型。此时再经阻抗分析仪测量得到此时边界条件下压电陶瓷的等效电路具体参数为电阻R1=88.176 kΩ，电容C1=1.677 6 nF，电感C1=350.31 H，电容C0=14.105 nF。若压电悬臂梁末端负载时，其等效电路具体数值为：电阻R1=18.06 kΩ，电容C1=2.503 5 nF，电感L1=149.95 H，电容C0=40.865 nF。

分别对压电陶瓷处于空载，负载和自由状态下的等效电路进行仿真分析，结果如图4所示。

图4 不同状态下电流特性放大图Figure 4 Current characteristic diagram in different states

针对3种不同边界条件下的压电陶瓷，其基频共振等效电路一致，但各等效元件具体数值不同，等效电路采集到振荡信号在振幅和频率上差异明显，故作为驱动器时压电悬臂梁的工作边界条件与其工作过程内部电流信号息息相关。

2.2 压电传感器电流特性

如图5所示，压电悬臂梁在工程应用中，末端弯曲到一定程度与限位装置发生碰撞，造成压电悬臂梁内部电流因正压电效应而改变，压电悬臂梁在该过程中可实现传感功能。冲击力F作用于压电悬臂自由端，为一非周期变化的的激振力，该力作用时间十分短暂，是典型的非周期作用下的响应。若v1和v2为系统受到冲击前后的速度，m为压电悬臂梁的质量，u为冲量大小，则有：

(2)

因为dt趋近于0，若要使Fdt为有限值，则F的值需要趋近于无穷大,此处冲量可以作为一个非常有意义的分析工具来量化力的大小。故可以将压电悬臂梁受外力冲击等效为受冲量作用的单自由度的欠阻尼系统，则：

(3)

式中：ζ为阻尼比，ωd为有阻尼振动时的频率，ωn为无阻尼振动时的固有频率，c为压电悬臂梁的阻尼系数，k为压电悬臂梁的等效弹簧常数。

等效弹簧常数为：

式中：E为材料的弹性模量，I为复合梁的横截面关于y-y方向上的惯性矩，I=bh3/12。

由于该压电悬臂梁上下2层为压电晶片，中间层为高碳纤维，所以需计算其等效的弹性模量，上下2层压电陶瓷厚度相同为h1,弹性模量为E1,中间基层厚度为h2，弹性模量为E2，令Ec为复合梁的等效的弹性模量，b为复合梁的宽，R为中性轴的曲率半径，弯矩为：

(4)

而M=EcI/R,因此从式(4)得到弯矩M后，即可求得：

(5)

根据挠曲线公式推出应变关于时间变化的规律:

(6)

由压电方程可知：

(7)

所用压电陶瓷片PZT-5H压电常数为d31，电极表面积为Ap，对电极表面积上的电位移量进行积分，可得到压电陶瓷传感器电极面输出电荷量的总和Q3为：

Q3=∬ApD3dxdy=Apd31T1。

(8)

联立式(5)～(7)解得：

(9)

(10)

综上，根据动力学方程以及压电方程求得压电悬臂梁在限位作用下与限位装置发生碰撞产生的电流随时间变化的规律。

2.3 驱动传感器共位电流特性

压电悬臂梁作为功能性驱动传感器，处于正常工作时，压电悬臂梁往返摆动，内部存在由其驱动等效电路产生的电信号；在该过程中因压电悬臂梁振动使得局部应变发生改变，产生并耦合了二次压电效应电信号。压电悬臂梁在限位边界条件下工作时，当压电悬臂梁末端未撞击到限位装置时，其内部电信号与未被限位时相同；撞击到限位装置的瞬间，因正压电效应在压电悬臂梁内部产生的电信号耦合进入压电悬臂梁正常摆动的信号之中，整个过程如示意图6所示，t1为压电悬臂梁撞击限位装置时间点，t2为截取共位信号结束的时间点。压电悬臂梁同时实现传感器和驱动器功能时，根据分析可知其内部电信号为线性耦合。

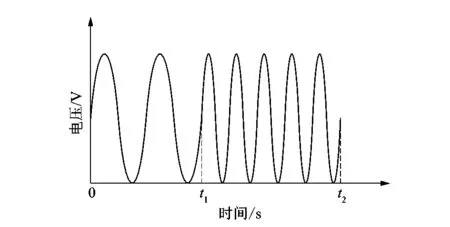
图6 共位信号产生过程Figure 6 Co-location signal generation process

3 实验

为验证压电悬臂梁驱动传感共位的电特性，课题组以压电双晶片悬臂梁为研究对象设计实验，分别对不同工作状态下压电悬臂梁内部电信号的变化进行分析比较，对上述理论及仿真进行验证。实验流程如图7(a)所示。

实验采用2组恒压源来控制输出加载电压，通过主控板控制输出电压的频率，并加载于压电悬臂梁上层压电晶片，使上层晶片作为驱动传感器。模拟压电悬臂梁的不同工作状态，经采样电路通过高性能示波器分别获取上层与下层压电晶片输出信号，最后由PC端进行数据处理并分析结果，样机平台如图7(b)所示。

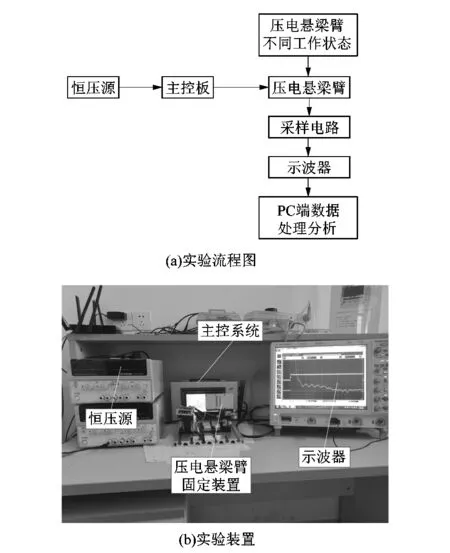
图7 实验流程及装置Figure 7 Experimental process and device

采用MATLAB对数据进行滤波处理，得到压电悬臂梁在空载正常工作时，上下2层压电晶片的采样信号，如图8所示。上层压电晶片因外部加载电场，所以其充电峰值较大，局部振荡信号相对较小。下层压电晶片作为传感器被动弯曲，因上下晶片极化方向相同，故而其信号与上层晶片输出信号相位角相差180°，且充电时峰值远小于上层压电晶片输出信号峰值。压电晶片输出信号充放电过程为其常见特性，其振荡信号特性为本研究重点，因此下文将取其局部振荡信号作为研究对象。

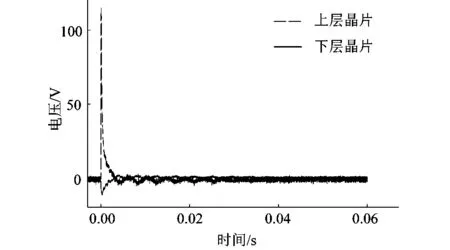
图8 空载条件下采样信号波形Figure 8 Sampling signal waveform under no-load condition

对压电悬臂梁在空载正常条件下与限位条件下局部采样信号进行分析，具体如图9所示。图9(a)为本次压电悬臂梁空载正常工作时经上下2晶片获取的电信号，该信号为压电悬臂梁作为驱动器产生的局部振荡信号及二次压电效应的耦合信号。图9(b)为在压电悬臂梁被限位时经上下2晶片获取的电信号，压电悬臂梁从平衡位置达到限位位置所用时间十分短暂，当压电悬臂梁撞击到限位装置的一瞬间，在冲击力的作用下经正压电效应压电悬臂梁内部产生电位移，耦合到压电悬臂梁作为驱动器产生的耦合信号之中，其内部电信号发生突变。下层压电晶片输出信号整体趋势与上层晶片一致。

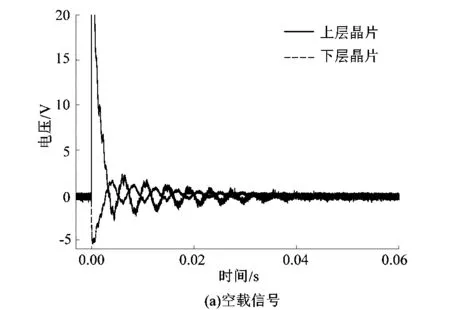
图9 不同工作条件下局部采样信号波形Figure 9 Local sampling signal waveform under different working conditions

由图10(a)和(b)可知，压电悬臂梁在空载条件下的仿真耦合信号频率为230 Hz,在受冲击力时的仿真耦合信号为1 690 Hz。如图10(c)与(d)所示，分别为上下2晶片在200 V电压激励下的不同工作条件下的响应频谱，经分析可知，在空载正常工作时，上下2晶片信号特征频率分别为226 Hz和244 Hz。由电路仿真可知，该信号仅为压电驱动器等效电路产生的信号，因此二次压电效应产生的电信号，在本研究中忽略不计。在限位工作时，上层晶片信号特征频率为239 Hz和 1 644 Hz，下层晶片信号特征频率为236 Hz和1 629 Hz，因此上层驱动压电晶片信号耦合了压电晶片作为传感器的电信号，验证了实验的准确性及可靠性。图10中纵坐标数值代表N/2倍的信号电压幅值，N为采样点数。

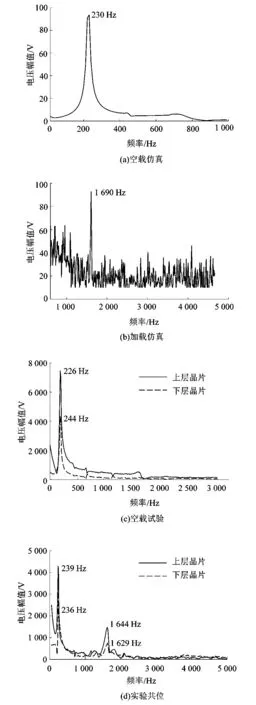
图10 信号频谱图Figure 10 Signal spectrogram

表3为压电悬臂梁在限位工作条件下时，不同激励电压下的采样信号频率及其与仿真耦合信号频率之间的误差，可以发现在不同大小的电压激励下，压电悬臂梁的采样信号频率与仿真耦合信号频率之间的误差低于4%，且压电悬臂梁在限位工作条件下存在频率值在230 Hz和1 640 Hz附近处的响应信号。

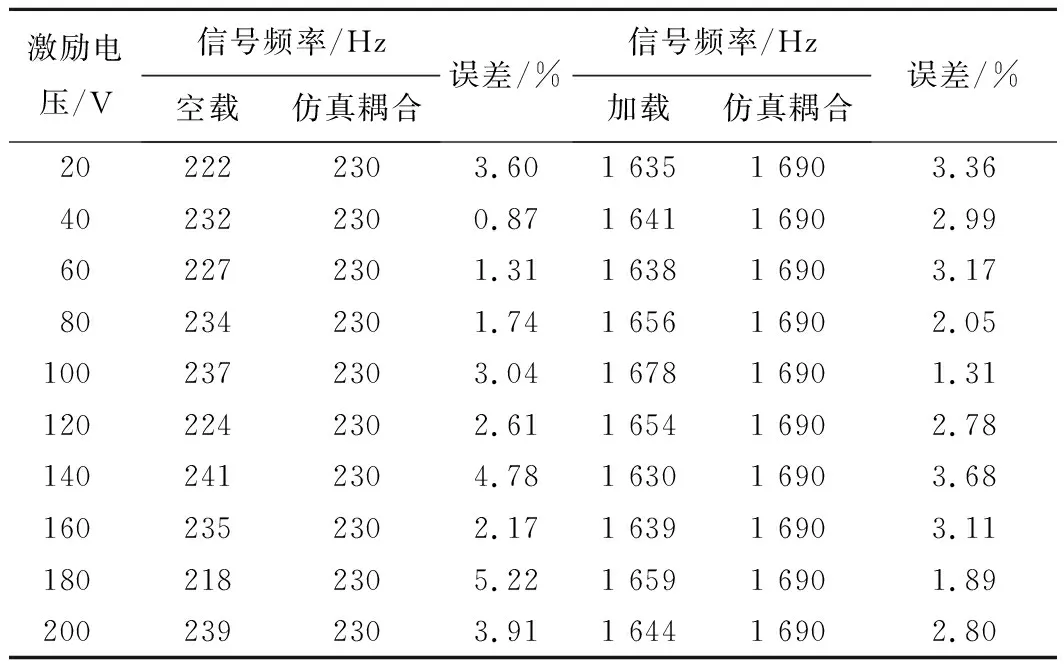
表3 实验信号频率采集结果

4 结论

课题组针对压电悬臂梁驱动传感共位特性进行研究，探究了压电悬臂梁分别作为传感器和驱动器的等效电路以及其内部电流的变化规律，分析了压电传感驱动器其电流特性为各种信号在时序上的线性耦合，建立了压电悬臂梁工作限位时的传感器输出电流与外部载荷的数学模型；通过ANSYSWorkbench有限元仿真软件模拟了压电悬臂梁在不同条件下内部电流变化，并设计了压电悬臂梁空载和限位2种工作状态实验。得到以下结论：①在未被限位正常工作时，在二次压电效应被忽略的情况下，其内部仅存在特征频率为230 Hz的响应信号；②在限位工况时，其内部存在特征频率频率分别约为230 Hz与1 640 Hz的响应信号。

针对压电悬臂梁作为驱动传感器共位信号特性的研究表明：该共位信号可作为压电悬臂梁驱动结果的衡量标准。因压电悬臂梁中间胶接层剥落或压电材料老化等因素出现压电悬臂梁动作不到位，可通过共位信号反馈出压电悬臂梁的工作状态,为智能驱动器在自检测、自诊断和自保护等领域提供了新方法，为压电陶瓷在微小驱动传感器领域以及驱动传感共位特性研究提供了思路，推动该领域的应用。该研究所探究的压电悬臂梁驱动传感共位特性在不同工程应用中，压电材料的边界条件不尽相同，后续可对在不同边界下、更多工况下其共位特性进行深入探究。