基于RBF神经网络的永磁同步电机控制系统

李瑞琦， 边火丁， 杨树炳， 张 华*

(1.浙江理工大学 机械与自动控制学院， 浙江 杭州 310018；2.浙江理工大学 浙江省现代纺织装备技术重点实验室， 浙江 杭州 310018；3.杭州汇坤控制技术有限公司,浙江 杭州 310005)

随着工业自动化技术的发展，在工业生产制造行业，永磁同步电机的应用越来越广泛。永磁同步电机具有着结构简单、省电、效率高和运行可靠等特点[1]。目前，永磁同步电机控制方式主要依然是传统PID控制。传统PID具有算法结构简单、方便移植等优点，但是面对生产中复杂的工况，尤其一些对于控制精度要求较高的应用场景，就很难满足控制需求[3]。

永磁同步电机在运行中，外部工况往往非常复杂，伴随着一些非线性因素的影响[4]，很容易受到外部扰动，由于很难对系统精确地建模，依靠人工调节PID控制器的参数，过程繁琐，且影响电机的正常运行[5]。近年来神经网络发展迅速，RBF神经网络具有结构简单、学习速度快的特点，且能够以任意精度逼近目标，能很好地避免局部最小的问题[6]。

课题组以永磁同步电机伺服系统速度环为研究对象，将径向基函数(Radical Basis Function，RBF)神经网络与PID控制器互相结合，并在Simulink中由RBF-PID在线对系统进行辨识，根据辨识得到的灵敏度信息整定PID控制参数，最后通过仿真验证了该方法的有效性。

1 永磁同步电机模型

在d-q坐标系下的永磁同步电机伺服系统[7]，其数学模型为：

电压方程：

(1)

式中：ud和uq分别为d轴和q轴上定子电压分量，Rs为定子电阻，id和iq分别为d轴和q轴上定子电流分量，Ld和Lq分别为d轴和q轴上定子电感分量，ω为转子机械角速度，Ψf为永磁体磁链，p为极对数。

电磁转矩方程：

(2)

式中Te为电磁转矩。

电磁转矩方程在有负载的情况下与负载转矩还应满足：

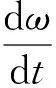
(3)

式中：TL为负载转矩,J为转动惯量,B为摩擦因数。

(4)

为了实现d轴和q轴的电流静态解耦，矢量控制时id=0，所以式(4)可以简化为：

(5)

由上述式子可以看出，永磁同步电机的数学模型具有非线性，并且和负载转矩关联性强。

2 径向基神经网络模型

RBF神经网络是一种前馈式3层神经网络，包括1层输入层、1层输出层和1层隐含层[8]，其网络结构如图1所示。

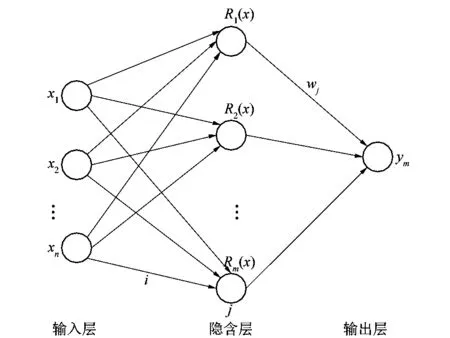
图1 RBF神经网络结构示意图Figure 1 Schematic diagram of RBF neural network structure

第1层输入层的输入为：

X=[x1,x2,…,xn]。

第2层隐含层径向基函数选取为高斯函数，高斯基函数具有形式简单、径向对称、光滑性好等优点，能够快速地逼近目标值[9]。高斯计函数表达式如下：

式中：cj为第j个节点的中心向量，bj为第j个节点宽度,‖*‖为欧几里得范数。

第3层的输出为：

ym(k)=w1h1+w2h2+…+wjhj。

式中：w1,w2,…,wj为节点权值。

RBF神经网络的性能指标函数为：

式中：e(k)为跟踪误差,y(k)为目标系统实际输出,ym(k)为神经网络辨识输出。

反向调节使用梯度下降法对输出权值、节点中心和节点宽度进行调整，梯度下降法具有形式简单、效率较高和局部寻优效果良好等优点，因此采用梯度下降法作为反向调节方法[10]。

节点的权值调节方法如下:

wj(k)=wj(k-1)+η[y(k)-ym(k)]hj+

α[wj(k-1)-wj(k-2)]。

式中：η为学习率，α为动量因子。

节点带宽参数调节方法如下：

bj(k)=bj(k-1)+ηΔbj+α[bj(k-1)-bj(k-2)]。

中心向量调节方法如下：

cji(k)=cji(k-1)+ηΔcji+α[cji(k-1)-cji(k-2)]。

辨识系统的Jacobian灵敏度信息如下所示：

3 基于RBF神经网络自适应PID控制

基于RBF神经网络整定的PID 控制系统结构如图2所示。其中Kp,Ki，Kd参数为在线调整方式，以克服系统的特性、运行工况而引起的模型变化。

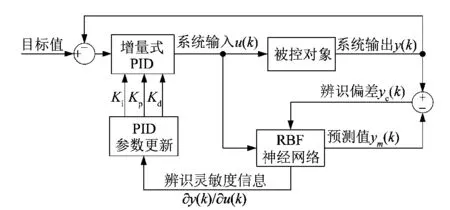
图2 RBF-PID结构Figure 2 RBF-PID structure

系统输入层为3层，分别为：

x1(k)=e(k)-e(k-1);

x2(k)=e(k);

x3(k)=e(k)-2e(k-1)+e(k-2)。

基于RBF神经网络自适应的PID 控制系统PID部分采用增量式PID，即：

u(k)=u(k-1)+Kp(k-1)x1(k)+Ki(k-1)·x2(k)+Kd(k-1)x3(k)。

式中：u(k)为系统输入,Kp为比例系数,Ki为积分系数,Kd为微分系数。

为克服系统非线性因素和扰动引起的系统模型变化，其中参数Kp，Ki，Kd根据辨识的灵敏度(Jacobian)信息进行在线调整，调整的方式如下:

4 系统仿真

为对比RBF神经网络PID控制器控制效果，在Simulink平台搭建了RBF-PID控制器和永磁同步电机模型，控制系统结构如图3所示，速度的设定值与实际速度的差值作为速度环PID控制器的输入，速度控制器产生转矩电流作为电流环PI控制器的输入[11]，然后对d-q轴电压PARK 逆变换得到a,b,c三相电压信号，最后通过PWM发生器控制逆变器驱动PMSM。

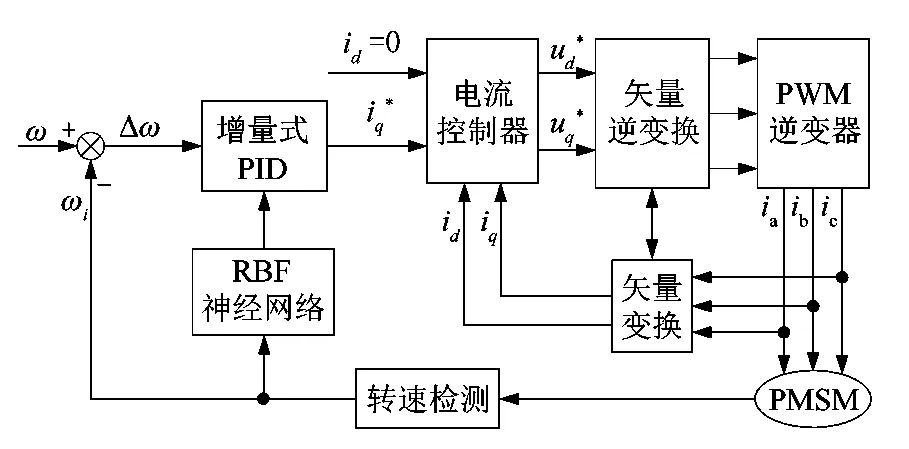
图3 系统仿真框图Figure 3 System simulation

其中速度环PID分别采用传统PID控制器和RBF-PID控制器，在初始PID参数参数相同的情况下对比系统的阶跃响应和负载发生扰动时的速度变化。系统Simulink仿真模型如图4所示，在仿真1.0 s时将速度设定值改为1 000 r/min，在2.0 s时加入负载扰动，在3.0 s时改变速度设定值为500 r/min。

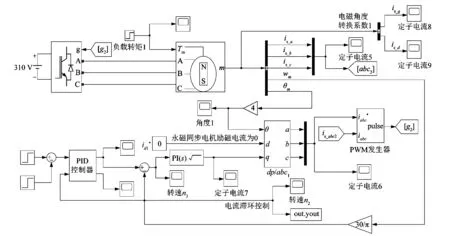
图4 系统Simulink仿真模型Figure 4 System Simulink simulation model

各种仿真结果如图5～8所示。由图6可以看出，当速度设定值改为1 000 r/min后，RBF-PID超调量比传统PID减少了60%，传统PID在1.1 s后稳态误差明显大于RBF-PID控制。由图7可以看出，在施加负载扰动后，传统PID与RBF-PID同时速度下降，在速度回升过程中，RBF-PID控制响应更快， 并且超调减少了40%。由图8可以看出，当速度设定值修改到500 r/min后，系统超调有了大幅的减少，并且响应时间减少了20%。

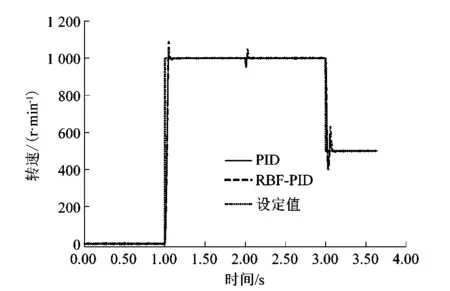
图5 仿真结果Figure 5 Simulation result

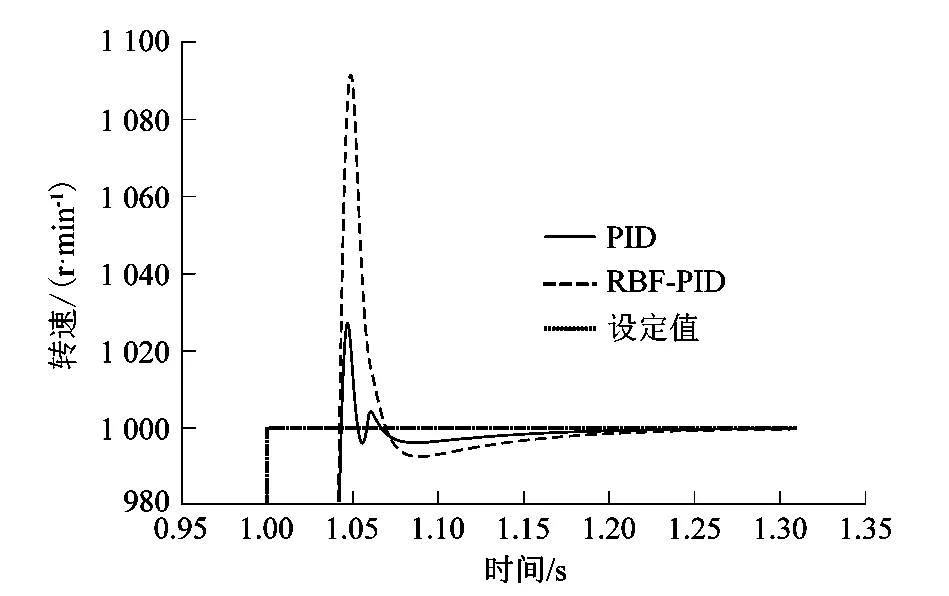
图6 速度阶跃响应波形Figure 6 Speed step response waveform

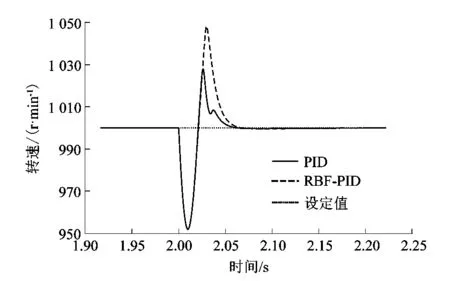
图7 负载扰动波形Figure 7 Load disturbance waveform

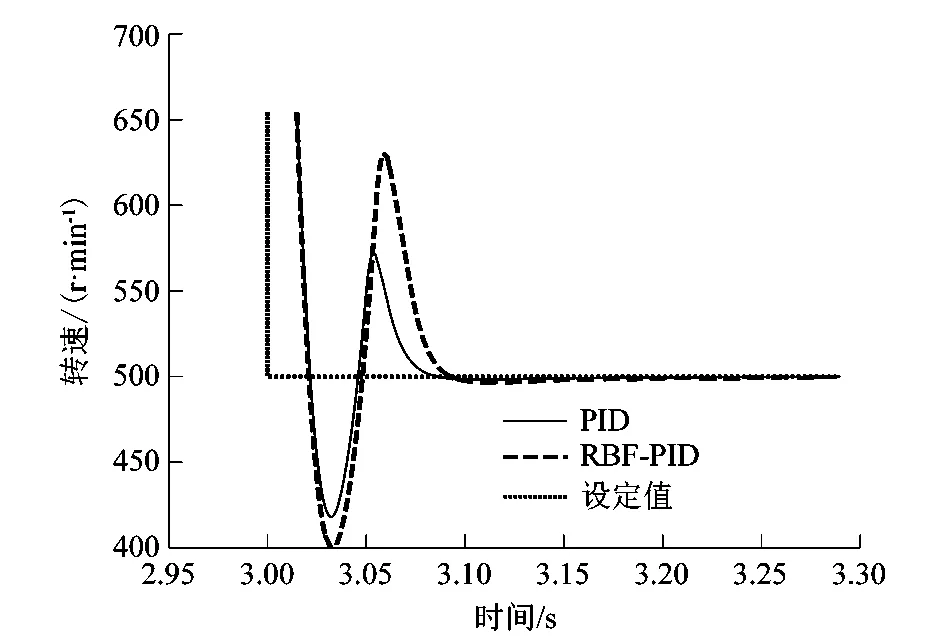
图8 速度降低波形Figure 8 Speed reduction waveform

综合来对比，RBF-PID有着更快的响应速度、更少的超调、更好的抗干扰能力，控制效果明显优于传统PID。

5 结语

针对永磁同步电机矢量控制系统，课题组设计了基于径向基函数(RBF)神经网络的PID控制器，根据神经网络辨识的灵敏度信息对PID参数进行在整定，通过在Simulink中进行仿真表明基于RBF神经网络的PID控制器控制效果更好。并且RBF神经网络节点较少，算法复杂度较低，后续可以在嵌入式控制设备中进一步移植与应用。