基于遗传算法的线路大型养路机械捣固作业单元区段选择模型

刘平

国能朔黄铁路发展有限责任公司肃宁分公司，河北肃宁 062350

随着我国经济的快速发展，铁路运输的需求也在不断增加，如何提高线路的运输能力已经成为亟待解决的重点问题之一。我国铁路网规模的进一步扩大，虽然极大地缓解了铁路运输能力的矛盾，但也造成了铁路基础设施养护维修作业量的迅速增加［1］。尤其是对于有砟轨道，维修作业时间较长的问题已经严重制约了铁路运输效率的提升。

目前，运维效率的提升主要依靠两方面：①不断优化工务维修管理模式；②建立高效、合理、最优的铁路线路养护维修计划模型，以捣固计划为例，可以分为中长期施工计划组织与短期施工计划组织两大类。

为提高运维效率，相关专家开展了一些研究。文献［2-3］结合我国高速铁路有砟轨道和无砟轨道维修特点，借鉴国外高速铁路工务维修管理经验，探讨了我国高速铁路工务维修管理体系的建立。文献［4］以轨道单元区段相邻两次大修之间的生命周期成本最小为目标，以何时安排捣固维修为决策变量，建立了相邻两次大修之间有砟轨道单元区段捣固维修及大修规划优化模型。文献［5］利用轨道质量指数（Track Quality Index，TQI），构建了有砟轨道状态修基准，以指导大型养路机械捣固作业计划的编制。文献［6］基于整数型轨道状态最优综合维修计划模型，构建了以遗传算法为基础的初步设想。文献［7］以养护维修时间为决策变量，以年度轨道不平顺平均值最小为目标函数，建立了整数型轨道状态最优的综合维修计划模型。文献［8］在需要维修的基本单元和天窗预留时间已知的前提下，针对给定天窗内铁路轨道大型养路机械维修（如大型养路机械捣固、钢轨打磨等）作业计划的编制，建立了以轨道设备状态最优为目标的优化模型。

既有研究模型多存在计算量大、缺乏现场操作可行性的问题。因此，本文立足于优化大型养路机械捣固维修计算效率与简化计划编制程序两个方面，将轨道综合养护计划模型分为轨道单元区段选择模型和大机作业分配模型两部分，通过建立轨道单元区段的选择模型来确定大机捣固作业地点，同时设计用于该模型求解的遗传算法，并利用线路轨道不平顺数据对模型及算法的有效性进行仿真研究，以期延长轨道结构的全寿命周期，确保铁路线路运行的可靠性。

1 捣固计划编制规则

限于各单位的大型养路机械捣固养护维修作业能力与工程实际要求，编制大机捣固计划应遵循如下规则。

1）养护总量约束。养护维修作业总量需小于大机作业能力。

2）养护次数限制。维修作业单元选择不存在包含属性，即单元区段选择时不能选择重复组。

3）养修工作之间存在先后关系。后养修计划需等之前的养修任务结束之后方可开展。

4）养护数量限值。大机作业车在同一时刻仅能作业一个单元区段。

5）恶化状态上限约束。对超过恶化上限值的单元进行定向指定，马上进行养护工作。

6）养护效率限制。大机捣固作业效率在不同单元区段作业时保持一致。

根据以上6条规则，以养护作业时间、地点为决策变量，以计划作业单元区段内所有组的养护改善量总和最大为目标函数，采用0-1整数型模型进行调度优化。

2 建立捣固计划编制模型

2.1 线路维修单位

在传统的轨道状态最优综合维修计划模型中，最优化对象是养护维修计划中全部的组。对于100 km线路，以100 m为基础单元，并按全年36旬进行养护维修计划的制定，那么解的形式是一个1 000×36矩阵，理论上矩阵中每个元素都可取0、1两个整数型变量，则模型解空间大小为，想得到严格的全局最优解是十分困难的。为解决原有单元捣固计划维修数据冗杂的问题，参考文献［9］提出的管理单元划分的基本原则和方法，提出了轨道单元区段选择模型，所得到的单元区段个数可以作为大机捣固作业分配模型的输入参数，并且成为养护维修计划输出解中矩阵的行数，增加模型求解效率。

根据养护机械作业范围和线路维修管理的需要，将计划维修的线路用组、单元区段进行划分，见图1。其中，组是轨道不平顺基本单位，以100 m区间范围内的轨道高低不平顺数值作为基础数据并计算标准偏差，组的长度可根据铁路公司具备的轨检仪器检测距离特征灵活选取；单元区段是计划编制单位，是由连续N个组的集合，N的取值需要考虑线路的天窗时间等实际作业情况来确定。经模型计算后的每个单元区段之间不一定连续，且区段内组的长度之和需小于可进行养护维修线路的长度之和。

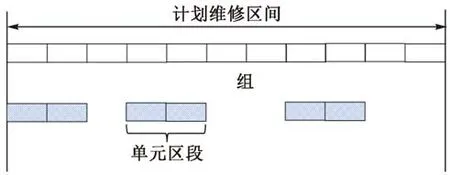
图1 计划维修线路划分

2.2 决策变量

轨道单元区段选择模型中，决策变量为0-1整数型变量，决策对象是组的集合L=｛1，2，…，Lmax｝。选择连续N个组，组成单元区段，连续区间中开始组的编号就是决策变量。

对于0-1整数型变量Vi（i∈L），Vi=1表示从组i开始N个组作为一个单元区段，Vi=0表示从组i开始N个组不能作为一个单元区段。

2.3 约束条件

1）单元区段选择理论约束

以组i为起点选择单元区段的情况下，从组i+1开始，将min｛i+（N-1），Lmax｝不能作为起点的组合成单元区段，即

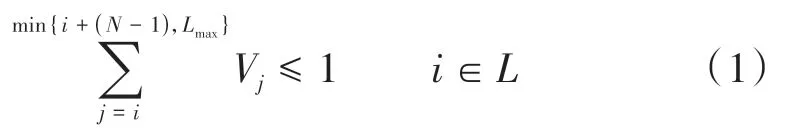
选定单元区段的起始组决策变量为1，其余组的决策变量都为0。理论约束不要求一定从初始里程处开始选，对两个连续单元区段之间的间隔也无要求，只需满足式（1），即组i被选中为某个单元区段中第一个组时，其后包括在这个单元区段中的组不能再成为其他单元区段中的一个组。

2）指定作业组约束

养护维修作业计划中必须进行作业的特定组，应包括在单元区段内，即

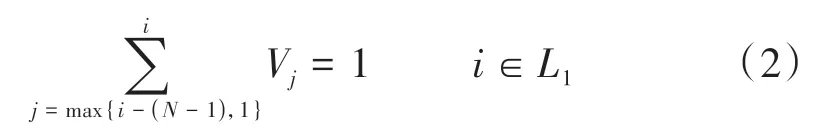
式中：L1为指定需要养护作业的组，如轨道不平顺在计划期内超过舒适性标准值但小于安全限值的组及有砟道床质量已明显不符合行车质量的组。

3）单元区段上限作业能力约束

考虑养护维修作业天窗时间和捣固机械的作业能力，将其作为养护工作量的上限，给出选择单元区段总数的最大值，即

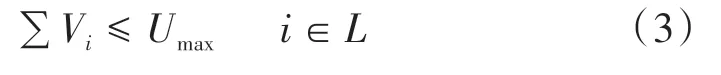
式中：Umax为可选择单元区段的上限。

2.4 目标函数

每条线路因其等级不同，列车的最高运行速度会有差别，即使是同一条线路，不同区段的实际最高运行速度也有不同。因此，在轨道不平顺标准差相同的情况下，不同线路区段的几何不平顺劣化状态也不尽相同。

引入参数r j，即实际养护改善量Δσj与各组的轨道不平顺标准差目标值σj之比。σj根据实际线路中列车速度不同，参照TG/GW102—2019《普速铁路线路修理规则》选取。r j可看作是每个组养护的优先度或必要度，表达式为

单元区段中N个组的养护改善量之和Si表达式为

取作业区间内的最大养护改善量之和Zmax为目标函数，即

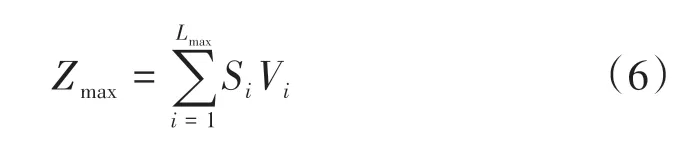
3 构建遗传算法求解

大机捣固计划编制模型实质上是0-1整数规划的最优问题。对于整数规划，一般可采用分支定界法、割平面法、隐枚举法等方法求解，但这些方法都要求约束条件的系数矩阵能由不含决策变量的系数精确表示。分析式（1）、式（2）可知，这两个约束的系数矩阵无法满足上述要求。因此，基于遗传算法对模型进行求解。

3.1 染色体编码

本模型决策变量采用矩阵编码的形式，为0-1整数型变量，一个行向量为染色体编码，向量列数表示线路中组的个数，Vi=1的位置为选中的单元区段起始点。

3.2 生成初始种群

一般生成初始种群的方法是在解空间中随机产生，但是这样得到的初始种群质量不高。因此，在初始种群生成之前，应进行最优区间估算，以免初始种群分布在远离全局最优解的编码空间，导致遗传算法的搜索范围受到限制，从而无法得到全局最优解，同时也为算法在时间复杂度上减轻负担。因此，本模型将式（6）的约束条件考虑到初始种群的生成中。步骤如下。

1）生成一个m×Lmax的全0矩阵A。其中m为初始种群的个体数，本文取100；

2）随机生成m×Umax的矩阵B。本例中Umax是一个固定值。B中每一行的随机数就是初始种群A中Vi=1的位置。本模型不考虑养护维修的成本问题，这里将单元区段上限作业能力约束简化为等式约束，并使初始种群中每一个个体都满足单元区段上限作业能力约束；

3）生成k×N的全1矩阵C，其中k为L1中组的个数。矩阵C每一行即为L1中一个指定作业组及其前N-1个组的编号；

4）在矩阵B中第i列随机产生矩阵C中第i行的N个数，相当于C要的数值可以涵盖在矩阵B中；

5）找到矩阵A每一行中对应矩阵B那一行的Umax个数，并将其赋值为1，这样就使得初始种群能满足指定作业组约束。

3.3 适应度计算

适应度函数的选择直接影响到算法能否收敛，个体的适应度值越大，其染色体被遗传下去的概率就越大。本文中目标函数取非负值，并且是以求函数最大值为优化目标，故可直接利用目标函数值作为个体的适应度。结合本模型，适应度评价函数f表达式为

3.4 遗传算子

1）选择算子

对种群模型采用轮盘选择法，根据优胜劣汰的原则，按个体适应度占种群所有个体适应度的比例来选择优秀个体。

2）交叉和变异算子

在遗传算法进行交叉变异过程中，按一定概率执行交叉和变异操作，且均采用单点操作，变异点处的个体基因保持不变。

为了有效避免该模型在计算时发生过早收敛的问题，在遗传到一定代数后，将会生成一定数量的新个体添加到既有种群中代替适应度低的个体，以此实现种群的全局最优解，避免出现局部最优解结束算法。

3.5 算法终止条件

遗传算法中常用的终止条件有两种［10］。①设置遗传终止进化代数T，通常T取100~1 000，这样既能保障模型的遗传迭代次数足够，也能够限制计算时间。②设置一足够小的数ε，当连续两代的最大适应度之差小于ε时终止，即

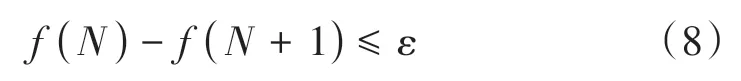
本模型采用以上两种方法共同作为算法终止条件，以保证该遗传算法的计算效率。

3.6 算法流程

遗传算法的流程见图2。

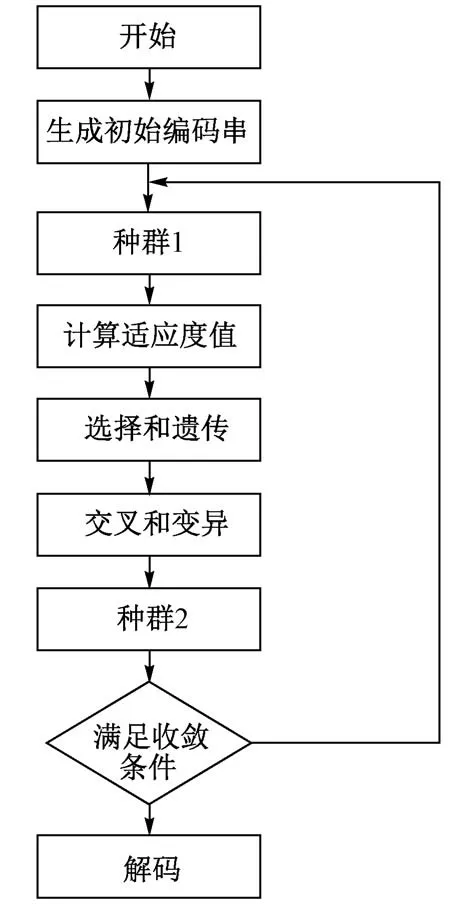
图2 遗传算法流程

4 算例应用

4.1 数据预处理

依据上述模型及遗传算法求解步骤，选取朔黄铁路2009年2月4日和2009年4月21日上行K226+000—K231+000的5 km高低不平顺数据，利用该遗传算法模型进行轨道单元区段自动选择，实现综合养护计划编制。

本模型计算范围为5 km，共计50个距离为100 m的组，即Lmax=50。该段线路列车的最高运行速度为200 km/h，高低不平顺的TQI管理值为1.5 mm，即σj=1.5。指定需要作业的单元组L1=［2，12，26，42］，最大作业轨道区段数量Umax=8，单元区段内组的个数为N=3。

4.2 轨道不平顺改善量的计算

对长度为100 m的组，设组i在t时的轨道高低几何不平顺标准差为σi(t)，在t+Δt时进行养护作业。在进行大机养护的情况下，组i经过Δt发展后的几何不平顺标准差为σi(t+Δt)。根据式（9）计算养护改善量，并由此计算下一次养护作业中改善量最大的组。计算结果见表1。

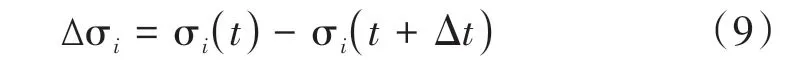
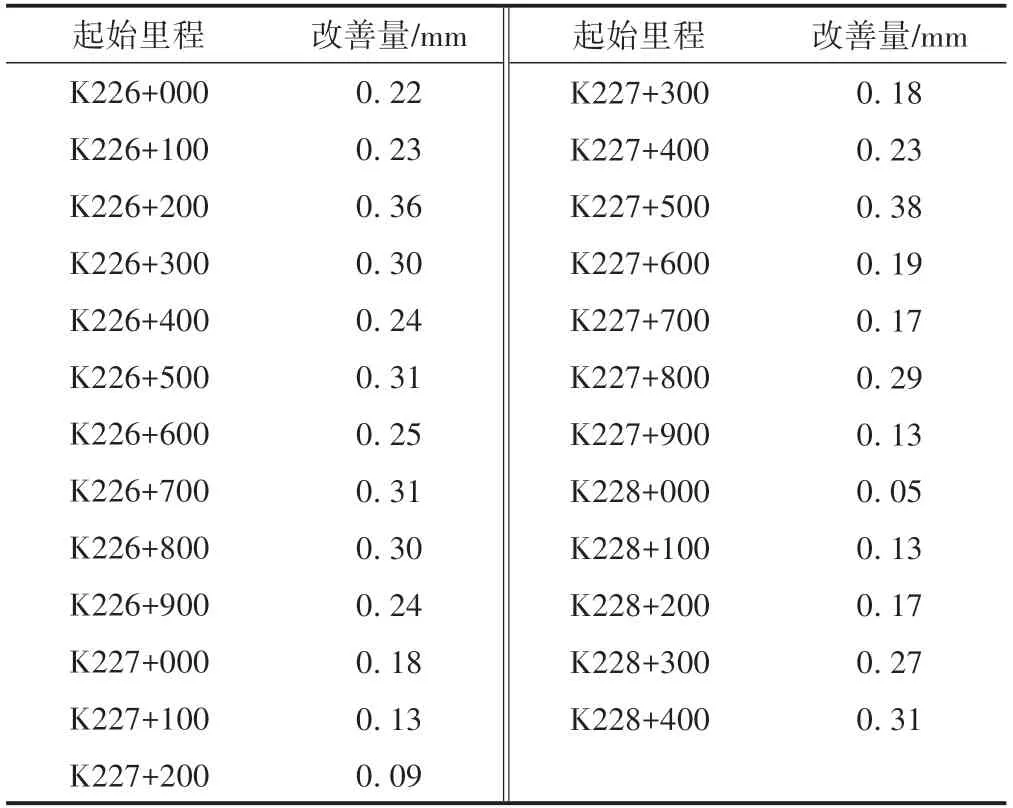
表1 高低不平顺实际改善量

4.3 遗传算法参数

模型计算采用轮盘选择法，按个体适应度占种群所有个体适应度的比例来选择优秀个体。种群个体的交叉、变异均采用单点操作，其中交叉概率取0.8，变异概率取0.1，以避免算法早熟，增加算法对新空间的探索能力，更好地收敛到全局最优解。

4.4 模型计算与结果分析

用MATLAB编写上述轨道单元区段选择模型代码，输入5 km的左高低不平顺改善量数据和相应的遗传算法参数，求解目标函数最大值与单元区段最优选择计划，并用枚举法编写计算模型进行比较，结果见图3。其中黑色为选定单元区段的起始组，与灰色单元共同组成选定维修区间的组。

图3 两种选择的轨道单元区段对比

用枚举法计算所得的目标函数值为4.46，计算时间大于2 h；用遗传算法迭代1 000次后，目标函数最大值为4.38，误差1.79%，随机运算10次的平均误差为9.57%，平均计算时间不到17 s。可见，遗传算法的计算效率更高，近似目标条件下约为枚举法的200倍。

5 结论

本文建立了轨道单元区段选择模型，并基于遗传算法实现了该模型的求解，结合轨道不平顺实测数据验证了模型及算法的效果。主要结论如下：

1）轨道单元区段选择模型的建立能有针对性地将人力、物力及有限的天窗作业时间用到最需要养护维修的轨道单元区段中，使轨道结构长期保持良好的平顺状态，从而进行更为经济、有效、合理的预防性养护维修管理。

2）通过本模型所选出的单元区段保证了在利用轨道状态最优养护维修计划模型安排大机捣固作业地点时，在各单元区段的养护周期内的养护改善量总和是最大的，降低了在制定轨道综合养护计划时产生维修灾难现象发生的可能性。

3）用遗传算法求解模型在效率上比枚举法有很大提高，同等约束条件下约为枚举法计算效率的200倍。