基于铁路货车动力学响应的轨面三角坑识别方法

2022-09-05谢博翟婉明陈是扦王开云

铁道建筑 2022年8期

谢博翟婉明陈是扦王开云，2

1.西南交通大学牵引动力国家重点实验室，成都 610031；2.兰州交通大学机电工程学院，兰州 730070

轨面三角坑会导致列车经过时轮轨作用力发生突变，从而引发车辆的侧滚和横摆，严重超限的三角坑将导致车辆转向架呈三轮支撑一轮悬浮的恶劣状态［1-2］，极大增加了列车倾覆、脱轨等风险，给列车行车安全带来了严峻挑战。因此，有必要开展运营线路轨面三角坑的常态化监测，及时发现超限区段并整改，以确保轨道健康，保障重载列车运输安全。

对于轨面三角坑检测，现有的技术手段主要包括基于人工的静态检测和基于轨道检测车的动态检测［3］。人工测量主要借助轨道检查仪和轨距尺，虽然检测精度较高，但是存在检测效率低且耗费大量人力物力、需要占用列车运营时间等局限。动态检测主要采用轨道检测车或综合检测列车，虽然改进了静态检测方法的不足，但使用成本较高，且不适合高密度线路的频繁测量，仍然很难满足轨面三角坑的常态化检测需求。现有的轨道静态和动态检测方法很难满足对轨面三角坑状态的快速、准确和及时的评估。因此，在运营车辆上安装检测装置并采集车辆关键部件动力学响应信号，开发相应的检测算法，是未来轨面三角坑检测技术的主要研究方向。

为了充分提取动力学响应中的有效检测信号，实现三角坑的准确识别，有必要引入先进的信号处理方法。目前，已有学者将集合经验模态分解（Ensemble Empirical Mode Decomposition，EEMD）方法［4］引入到轨道故障检测中。文献［5］基于EEMD和希尔伯特变换实现了道岔区轨道不平顺局部特征的提取与定位。文献［6］将运营车辆作为检测车辆，利用车辆轴箱监测数据，基于EEMD建立一种轨道缺陷监测方法。文献［7］提出基于EEMD和奇异值分解的方法解决钢轨波磨数据中的轨道起伏趋势提取问题，可用于钢轨波磨检测。文献［8］基于EEMD提出声学诊断的方法，实现对钢轨波磨区段的识别。此外，EEMD也广泛应用于其他故障检测领域［9-10］。EEMD在轨道三角坑检测中的应用尚未见报道，有待研究将该方法进一步应用于车辆动力学响应特征信号提取以实现三角坑的准确识别。

本文以我国C80货车为研究对象，搭建车辆动力学模型，基于车辆左右两侧二系动态位移响应（即车体与侧架相对位移）实现轨面三角坑检测。该方法首先利用EEMD结合峭度加权法提取出车辆左右两侧二系动态位移差的有效信号成分，然后利用改进后的能量比（Modified Energy Ratio，MER）法定位位移差合成信号中所包含的三角坑，为基于运营车辆的三角坑动态检测方法研究提供理论依据。

1 方法与原理

1.1 EEMD法

EEMD法是在经验模态分解（Empirical Mode Decomposition，EMD）基础上提出的一种改进方法［4］。该方法通过在EMD上加入白噪声信号并进行集合平均，可有效抑制EMD分解方法的模态混叠和端点效应，自适应地将信号分解为一系列本征模态函数（Intrinsic Mode Functions，IMF）分量。因此，EEMD在EMD的基础上增加所添加的白噪声序列数目N和标准差εn的参数设定。EEMD法的主要步骤如下。

1）在待分析信号s(t)中多次叠加等长度的白噪声序列N i(t)，构造新的信号序列s i(t)，表达式为

2）对加入白噪声后的信号进行EMD处理得到多个IMF。

3）重复以上步骤，每次加入相同振幅的新生白噪声序列，得到多次分解的IMF分量。

4）将每次分解得到的IMF分量集合平均，消除加入白噪声的影响，得到第j个IMF分量C j(t)为

式中：C ij(t)为第i次添加白噪声后的第j个IMF分量。

1.2 改进的能量比法

能量比算法定义为相邻两个时间窗内信号的能量比值E，表达式为

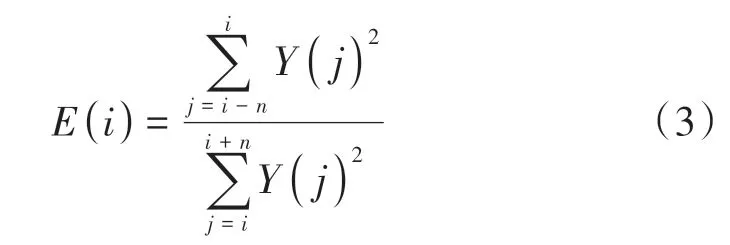
式中：Y为信号幅值；n为时间窗内的采样点数。

在此基础上，利用提出的MER法计算改进后的能量比值M，计算式为［11］

MER曲线的峰值表示待检测信号的特征突变位置，本文中的MER曲线峰值对应线路上轨面三角坑的位置。

1.3 三角坑检测算法流程

采用EEMD法分解车辆左右两侧二系动态位移差信号，并结合峭度指标权重重构分量信号，实现有效信号提取（提取后的位移差称重构位移差），然后利用MER法准确定位轨面三角坑。算法流程见图1。

图1 三角坑检测算法流程

具体步骤如下：

1）采集车辆左右两侧车体与侧架相对位移数据，将两侧位移数据相减后得到差值信号f(t)。

2）定义EEMD白噪声序列的数目N和标准差εn，利用EEMD将信号f(t)分解为m个IMF分量u1，u2，…，u m。

3）计算各IMF信号分量峭度指标k，并根据式（5）计算出各IMF分量重构权重a，然后根据式（6）重构出有效信号Y。

式中：umax为IMF分量中峭度值最大的信号分量。

4）选择合适的MER法计算窗口尺寸，检测重构信号突变位置，即可定位出轨面三角坑位置。

2 仿真验证和分析

2.1 车辆动力学模型

基于我国实际运营的C80型货车参数，在SIMPACK中建立铁路货车动力学模型。建模过程中考虑车身、侧架、摇枕、轮对等关键结构部件，各部件间均采用弹簧阻尼系统模拟悬挂连接，见图2。货车模型共包含39个自由度。其中，车体和轮对考虑除纵向外的5个自由度，摇枕仅考虑摇头运动自由度以及侧架的纵向、横向和摇头自由度。有关动力学模型车辆结构和动力学参数参见文献［12-13］。

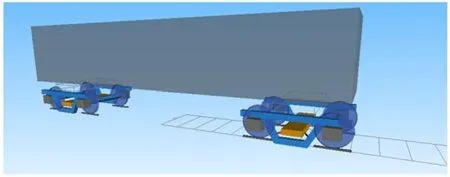
图2 动力学仿真模型

2.2 轨面三角坑设置

轨道三角坑（即扭曲不平顺）是指两股钢轨顶面相对于轨道平面发生扭曲变形，钢轨在一定距离内先左股高于右股，然后是右股高于左股，反之亦然［1］。仿真时，分别在左右两股钢轨设置波长为D、幅值为A的谐波不平顺，且相位差为D/2，如图3所示。同时在轨道上施加美国五级谱轨道不平顺，模拟运营货车的实际运行工况。

图3 轨面三角坑示意

2.3 三角坑动力学特征

基于上述动力学仿真模型与轨面三角坑设置方式，计算车辆以60 km/h通过基长为3 m，幅值分别为2.8、6.8、10.8 mm的三角坑时车辆左右两侧二系（车体与侧架）动态相对位移响应，见图4。可以看出，当三角坑幅值较小时，车辆左右两侧相对位移较其他区段变化不显著，但随着三角坑幅值逐渐增加，车辆左右两侧相对位移也随之增大。

图4 车辆左右两侧二系动态相对位移

计算车辆左右两侧相对位移差，结果见图5。可以看出，相对位移差在三角坑区段随着三角坑幅值增加而增大，且对于同一三角坑幅值，相对位移差与单侧相对位移相比具有特征放大的效果。这是因为车辆通过三角坑区段时，转向架左右两侧车体与侧架相对位移表现出一侧增加而另一侧减小的变化趋势，求取两侧相对位移差可将这一信号特征增强。

图5 车辆左右两侧二系动态相对位移差

综上，可将车辆左右两侧二系相对位移差作为三角坑检测的敏感动力学特征信号。此外，该动力学响应在实际运营车辆中便于测量，在现场应用中也具备可行性。因此，利用该动力学响应特征信号进一步采用信号处理方法提取出有效信号成分更易于实现三角坑的识别。

3 三角坑检测方法

3.1 基于EEMD的有效信号提取

三角坑检测方法仿真分析中共设置400 m轨道不平顺，并将三角坑设置在里程77.24 m处。以相对位移特征变化最小的三角坑（幅值2.8 mm）为例进行有效检测信号的进一步提取分析，验证本文所提出方法的适用性。位移差合成信号提取过程见图6。其中，图6（c）为图6（a）和图6（b）中两侧相对位移求取差值后的结果。可以看出，在三角坑线路区段，相对位移差有明显的特征增强效果。

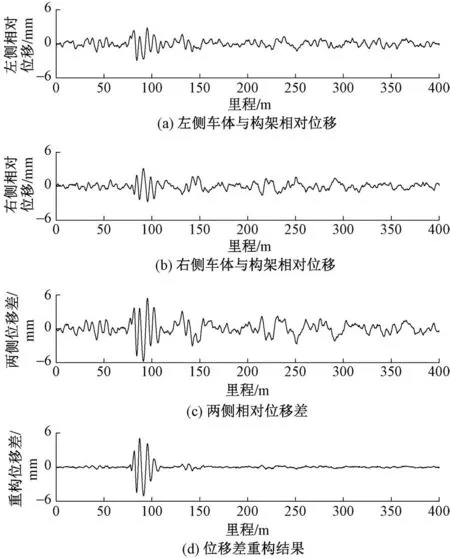
图6 位移差合成信号提取过程

对两侧相对位移差信号进行有效信号提取。首先，采用EEMD法分解位移差信号，参数选择N=200，εn=0.2，部分分解结果见图7。可以看出，位移差信号被分解为由高频波动到低频波动的多个IMF信号分量。其中部分分量包含由三角坑引起的信号特征，绝大部分分量中主要包含由轨道不平顺等引起的噪声成分。然后，计算各IMF分量峭度值，结果见图8。

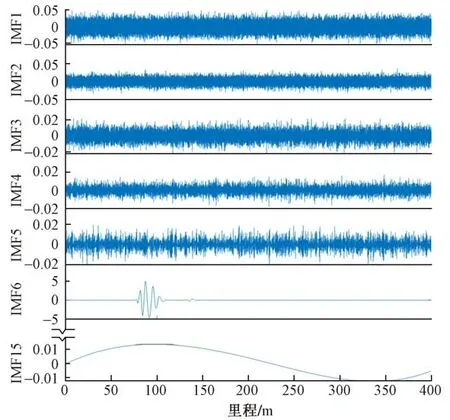
图7 位移差信号EEMD分解结果

图8 IMF分量峭度值

根据本文所提出的IMF分量重构规则，按式（5）和式（6）重构出有效信号分量，将峭度值最大的第6个IMF分量保留，其余分量依次按照各自峭度权重加权组合即可获得用于三角坑定位检测的位移差合成信号［参见图6（d）］。与两侧位移差［参见图6（c）］相比，有效的信号成分从包含各类干扰因素的混合信号中分离出来，由三角坑引发的车辆二系相对位移变化特征得到进一步增强，更有利于三角坑区段的精准识别。

3.2 三角坑定位方法研究

基于提取出的位移差合成信号（重构位移差），采用MER法拾取信号突变位置来定位线路中轨面三角坑。确定MER滑动时间窗尺寸为2 300个采样点，依次对幅值为2.8、6.8、10.8 mm的三角坑进行定位识别，结果见图9。可知：MER曲线的峰值位置对应三角坑的识别结果分别为77.21、77.22、77.20 m，与真实三角坑位置（里程77.24 m）相比具有较高的定位精度，仿真研究结果表明定位误差可控制在0.1 m范围内。