不规则缺陷管道失效压力影响因素及评价方法
2022-09-05孙明明方宏远赵海盛
孙明明,方宏远,赵海盛,李 昕
(1.郑州大学水利科学与工程学院,河南郑州 450001;2.大连理工大学海岸和近海工程国家重点实验室,辽宁大连 116024;3.大连理工大学工程抗震研究所,辽宁大连 116024)
承压钢质管道作为远距离运输中最经济的方式之一[1-2],其结构完整性评价是工业界和石油工程的一个重要研究领域。管道内输送的腐蚀性介质和管道外海水、土壤中的腐蚀性物质,常在管道内外壁产生局部腐蚀缺陷。根据单个腐蚀缺陷在轴向平面上投影的形状,可以将单个腐蚀缺陷分为规则形状和不规则形状。如果腐蚀缺陷的深度分布呈现一个或多个极值点,则可以将其视为不规则形状。不规则形状缺陷的内压承载力与缺陷深度轮廓密切相关,随着缺陷总长度增加,不规则形状缺陷失效行为的复杂性增加。在实际工程中,通常采用一级和二级评价方法预测管道的失效压力。传统方法是一级评估方法,如ASME-B31G方法[3]、RSTRENG 085dL方法[4]、RPA方法[5]和DNV-RP-F101单点评价方法[6]。二级方法用于评估不规则形状缺陷,例如不规则形状缺陷的DNV-RP-F101方法[6]和有效面积方法[4]。巴西国家石油公司针对不规则形状缺陷管道性能的研究表明二级评价方法精度高于一级评价方法[7-8]。尽管二级评估方法更为精确,但计算的复杂度和工作量远大于一级评估方法,因此需要一种更有效、准确的方法来评估不规则形状缺陷的失效压力。笔者通过建立不规则缺陷管道有限元模型,对不规则缺陷管道失效压力的影响因素进行分析,并结合有限元模型结果,基于等效形状的有效深度得到一种更准确、更有效的评估方法,通过与试验结果进行对比,验证新方法的有效性。
1 有限元模型建立与验证
为了研究不规则形状缺陷对失效压力的影响,建立了钢管的有限元模型并进行分析[9]。基于通用有限元软件ANSYS,对腐蚀管道的破坏行为和极限强度进行有限元分析。
1.1 不规则缺陷管道有限元模型
DNV-RP-F101规范指出:不规则腐蚀缺陷可以简化为一个浅腐蚀区域内包含有一个或几个的深腐蚀缺陷。本文针对典型的不规则缺陷模型:浅腐蚀缺陷中含有一个或两个深腐蚀缺陷的缺陷进行研究。管道材料为API-5L-X80,实测的材料屈服强度σy为601 MPa,工程抗拉强度σu为684 MPa。根据Benjamin对API-5L-X80的研究结果,采用Ramberg-Osgood模型模拟其真实应力-应变曲线[10-11]:
(1)

X80的真实应力-应变曲线如图1所示。
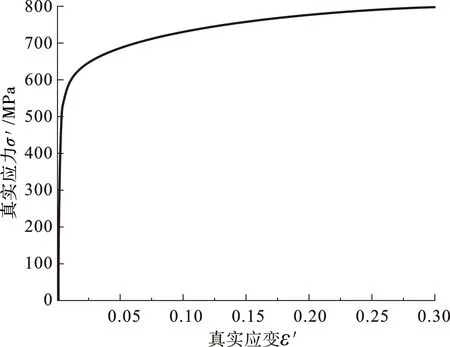
图1 API X80 的真实应力-应变曲线Fig.1 True stress-strain relationship for API X80 pipeline steel

图2 不规则形状缺陷有限元模型Fig.2 Finite element model(FEM) with irregular-shaped corrosion defect
采用20节点的六面体实体单元建立有限元模型。考虑到管道几何形状、内压荷载的对称性,选取1/4管道建立有限元模型,如图2所示。缺陷沿厚度方向分为4层,在应力集中的腐蚀区域内采用细网格,粗网格应用于应力均匀的地方,同时考虑了粗细网格之间适当的梯度。因为只取1/4管道模型进行模拟,因此在管道对称截面处施加垂直于该截面方向的对称位移边界条件。管道模型被扩展到离腐蚀区域足够远的地方,以防止边界条件影响相关区域的应力;对腐蚀坑进行倒角处理,以将应力集中效应降至最低。
1.2 内压失效判别准则
采用被称为“剩余壁厚应力准则”的破坏准则[12]:当缺陷中剩余壁厚的最小von Mises应力超过材料的真实极限抗拉强度时,管道发生破坏。
Andrade等[10-11]将该准则应用于含有腐蚀缺陷的API-5L-X80钢管试件的非线性有限元分析,通过有限元模型预测的失效压力与试验室爆破试验测得的失效压力进行对比,结果表明当腐蚀管道材料等级为X80时,“剩余壁厚应力准则”能给出准确的失效预测。
1.3 有限元方法验证
在采用有限元模型进行失效分析之前,必须对模型进行验证。Freire等[13]对仅承受内压的不规则形状缺陷的管道进行一系列全尺寸爆破试验。在这些试验中选择实例TS 5.2和TS 5.3验证本研究中的有限元模型。验证试验的管道缺陷是一个长而浅的腐蚀,上面有两个深腐蚀缺陷;缺陷区域的形状为矩形,边缘光滑。表1为通过有限元分析和试验测得的钢管失效压力,这两个值之间的平均误差约为2.29%。由此可知有限元计算结果与试验结果吻合良好,验证了本文模型的正确性。

表1 有限元计算结果对比Table 1 Comparison of FEM result and measured failure pressure
2 深腐蚀缺陷相互作用
2.1 计算工况
对于具有不规则形状缺陷的腐蚀管道,考虑浅部腐蚀缺陷包含两个深部腐蚀缺陷的情况。苏晨亮[14]、Li等[15]的研究成果表明相邻缺陷的极限间距主要受管道尺寸的影响,而受管材强度等级影响较小,因此本文采用API 5L X80钢管进行深腐蚀缺陷的相互作用研究。管道外径D和壁厚t分别为457.2和9.53 mm,缺陷形状如图3所示,图中SL为两个深腐蚀缺陷之间的轴向间距,wd、Ld和dd分别为深腐蚀缺陷的宽度、长度和深度,ws、Ls和ds分别为浅腐蚀缺陷的宽度、长度和深度,LL和LR分别为深腐蚀缺陷距离轴向左边界和右边界的距离,w为深腐蚀缺陷距离缺陷环向边界的距离,单位均为mm。
以Freire[13]的试验为参考,取浅腐蚀缺陷深度ds/t=0.3,浅腐蚀长度Ls=384 mm,浅腐蚀宽度ws=86.5 mm;深腐蚀缺陷深度dd/t=0.63,腐蚀长度Ld=64 mm,腐蚀宽度wd=43.25 mm。计算工况如表2所示,其中工况1-1~1-4为一个浅腐蚀缺陷包含两个深腐蚀缺陷的工况编号。基础工况为一个浅腐蚀缺陷内只含一个深腐蚀缺陷形式的管道工况,其极限失效内压为19.02 MPa,该工况为分析深腐蚀缺陷之间是否存在相互作用的基础。
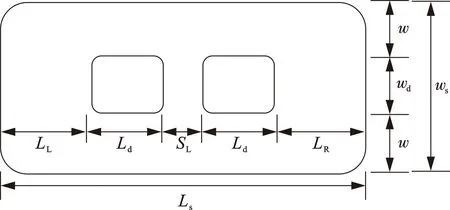
图3 不规则缺陷尺寸示意图Fig.3 Dimensions of irregular-shaped defect

表2 计算工况参数Table 2 Parameters of colonies
2.2 计算结果
采用与基本腐蚀缺陷极限内压比值pf/pB来描述深腐蚀缺陷间距对其极限失效压力的影响,其中pB为基础工况的极限内压承载力。认为当pf/pB大于等于0.99时,深腐蚀缺陷之间的相互作用可以忽略[15]。表3列出了表2各组工况的有限元计算结果以及对其是否有相互作用的判断结果。由表3中看出,失效压力是随着深腐蚀缺陷轴向距离的增大而逐渐增大,其失效压力也逐渐趋近于基本腐蚀缺陷的失效压力。

表3 各组工况的有限元模型极限内压承载力Table 3 Failure pressures of FEM of colonies cases


图4 失效压力随轴向间距变化Fig.4 Variation of failure pressure with different axial spacing
3 深度剖面对失效压力影响
由于多个深腐蚀缺陷的相互作用可以等效为一个缺陷,因此采用浅腐蚀缺陷中含有一个深腐蚀缺陷的不规则形状缺陷分析深度剖面与失效压力之间的关系,含有一个深腐蚀缺陷的不规则形状缺陷的形状如图5所示。
表4为深腐蚀缺陷的尺寸和工况,其中浅腐蚀缺陷的尺寸保持不变,工况2-1~工况 4-5为一个浅腐蚀缺陷包含一个深腐蚀缺陷的工况编号;表4中最大缺陷深度d与缺陷平均深度da比值d/da为不规则缺陷深度剖面不规则程度的度量,其中da=A/Ls,A为不规则缺陷轴向投影面积。组合一中每个工况的dd都不同,用于分析dd/ds对失效压力的影响;组合二中每个工况的Ld不同,用于分析Ld/Ls对失效压力的影响;组合三中每个工况的wd不同,用于分析wd/ws对失效压力的影响。

图5 含有一个深腐蚀缺陷的不规则缺陷示意图Fig.5 Dimensions of irregular-shaped defect including one deep defect
失效压力表示为
(2)
式中,p0为完好管道失效压力,MPa;σu为工程抗拉强度,MPa。
图6为不规则形状缺陷的失效压力相对于Ld/Ls、wd/ws和dd/ds的变化。由图6可以看出,除wd/ws之外,随着深腐蚀缺陷长度和深度增加,不规则缺陷管道失效压力均呈现下降趋势。浅腐蚀缺陷的宽度对不规则形状缺陷管道失效压力影响很小,可以忽略不计。随着dd/ds增大,管道的失效压力下降显著,且dd/ds越大,失效压力pf下降速度越快。与之不同的是,失效压力随着Ld/Ls增加,几乎呈线性下降趋势。
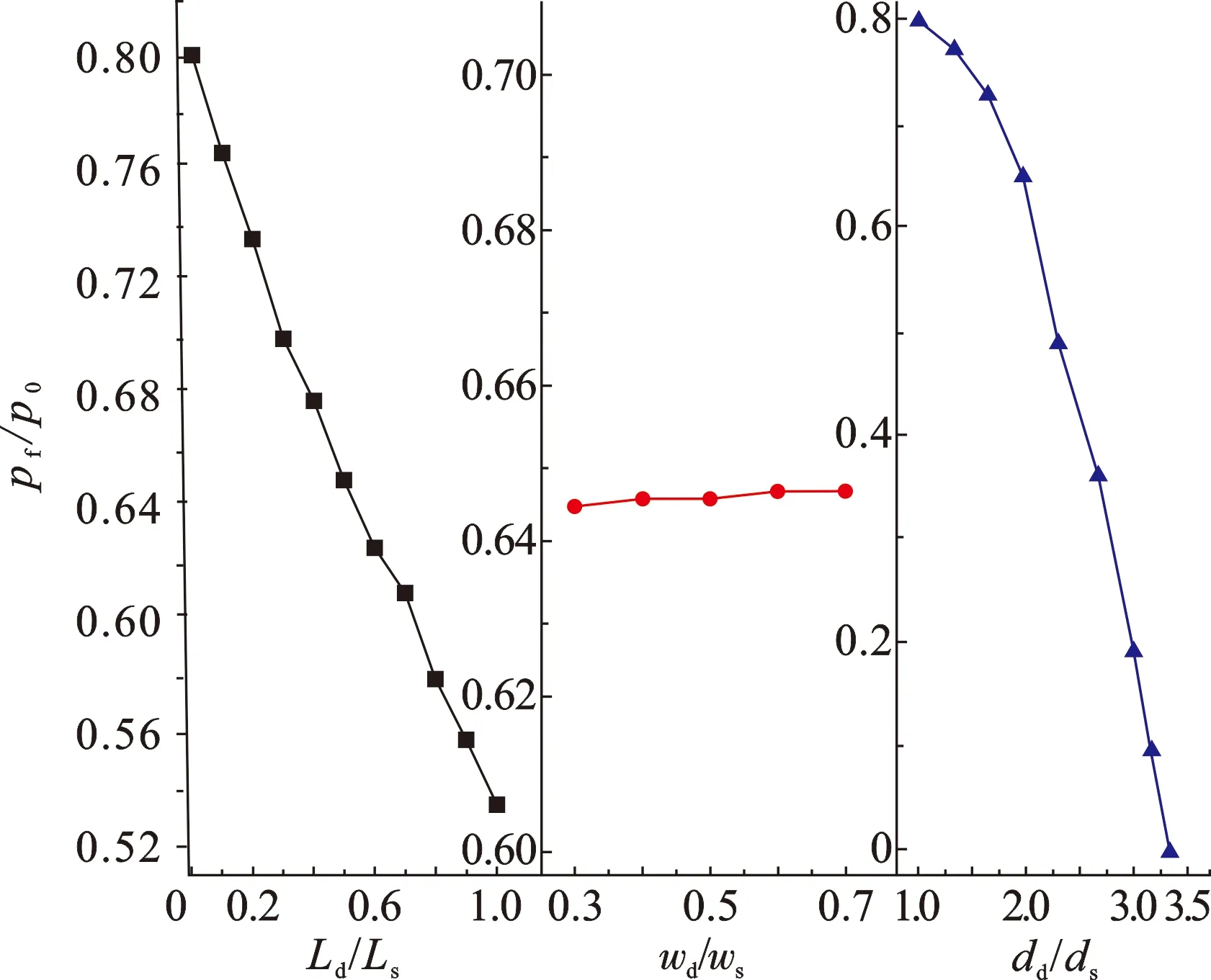
图6 不同深腐蚀缺陷下失效压力变化Fig.6 Variation of failure pressure with respect to deep defect with different sizes

表4 含有一个深腐蚀缺陷的不规则缺陷参数Table 4 Parameters of different cases with one deep defect
4 不规则缺陷管道失效压力计算

不同的等效形状可以得到不同的最大深度。为得到不规则腐蚀缺陷真实等效深度de,采用适用范围广泛且准确度较高的DNV-RP-F101标准进行反演计算,该规范中失效压力表示为
(3)
(4)
式中,Q为长度矫正系数;de为真实等效深度,mm。
根据式(2)和(3)可以反演得到不规则缺陷真实等效深度de计算公式,表示为
(5)
矩形等效形状的等效深度为dr=A/Ls,抛物线等效形状的等效深度为dp=A/(2/3Ls),两者折中等效形状的等效深度为d0.85=A/(0.85Ls)。不同等效形状的等效深度如图7所示,dr数值最小,dp数值最大,d0.85处于中间。采用抛物线形状等效深度预测失效压力最为保守,采用矩形形状等效深度预测失效压力最为危险。抛物线形状的等效深度dp是真实等效深度de的上限,矩形形状的等效深度dr是真实等效深度de的下限,因此采用dr和dp的线性组合表示真实等效深度de。

图7 等效深度示意图Fig.7 Effective depth diagram
对于不同不规则度的缺陷,d/da是定义不规则缺陷的参数。1.0≤d/da≤1.2的缺陷属于规则形状缺陷,d/da≥1.2时的缺陷被归类为不规则形状缺陷[16]。选择表4中不规则缺陷算例工况 2-3~2-8、工况 3-2~3-7和工况 4-1~4-5进行分析,考虑到极端情况下的完好管道,de=dr=dp=0,因此拟合公式常数项为0。等效深度拟合公式为
de=α1dr+α2dp.
(6)
式中,α1和α2为拟合参数,对于d0.85,参数α1=α2=0.5。
结合不规则算例,参数α1和α2拟合结果分别为0和0.759。决定系数R2=0.974,拟合程度较好。根据式(6)可以计算等效深度de,结合腐蚀长度Ls和等效深度de,由式(3)可计算失效压力。
5 不规则缺陷失效压力评估方法验证
5.1 不规则缺陷爆破试验
巴西国家石油公司(PETROBRAS)对不规则缺陷管道进行了内压爆破试验。试验管道包括低、中、高强度钢(X42、X46、X60和X80),腐蚀类型包括人工腐蚀和天然腐蚀,试验数据见表5。

表5 试验数据Table 5 Test data
为了增加不规则缺陷内压爆破试验的全面性,采用大连理工大学自主研发的复杂荷载试验机进行不规则缺陷管道的爆破试验IDTS(irregular-shaped defects test specimen)。该管道平均外径为357.8 mm,管壁平均壁厚为12.66 mm。不规则缺陷由1个浅腐蚀缺陷和3个深腐蚀缺陷构成,其中3个深腐蚀缺陷尺寸各不相同,相互间距及相互影响程度也各不相同,该工况可作为表6不规则缺陷试验的补充。
试验工况IDTS不规则缺陷尺寸和示意图如表6和图8所示。不规则缺陷的不规则度为d/dave=8.59 mm/5.82 mm=1.47>1.2,满足不规则缺陷定义。经过环向试件的单轴拉伸试验测得管道环向平均屈服强度和平均抗拉强度分别为378.9和534.2 MPa。

表6 IDTS腐蚀缺陷尺寸Table 6 Dimensions of defects of IDTS mm
5.2 失效压力误差
采用6种现有方法进行失效压力评估,分别为一级评估方法中的ASME B31G方法[3]、RSTRENG 085dL方法[4]、DNV RP-F101方法(单点)[6]和RPA方法[5];二级评估方法的RSTRENG有效面积法[4]和DNV RP-F101方法(不规则形状)[6]。
表7为不同工况的平均误差分析。在所有不规则形状缺陷管道实际爆破试验中,本文的数值方法平均误差为10.87%,为所有评估方法的最小值,准确度最高。现有评估方法中DNV-RP-F101方法(不规则形状)评估方法误差最小,其次为RSTRENG有效面积法,由于一级评估方法未考虑缺陷的不规则性,二级评估方法的精度远大于一级评估方法精度。对于两种常用的二级评价方法:有效面积法和DNV(不规则形状),两者并无明显的优劣差异性。
需要指出的是无论二级评估方法中的DNV-RP-F101方法(不规则形状)还是RSTRENG有效面积法,都需要对缺陷范围内所有可能失效的区域进行评估,评价步骤相对于本文数值方法更为繁琐。本文中提出的数值方法基于缺陷长度和缺陷投影面积进行失效压力评估,操作更为简便。
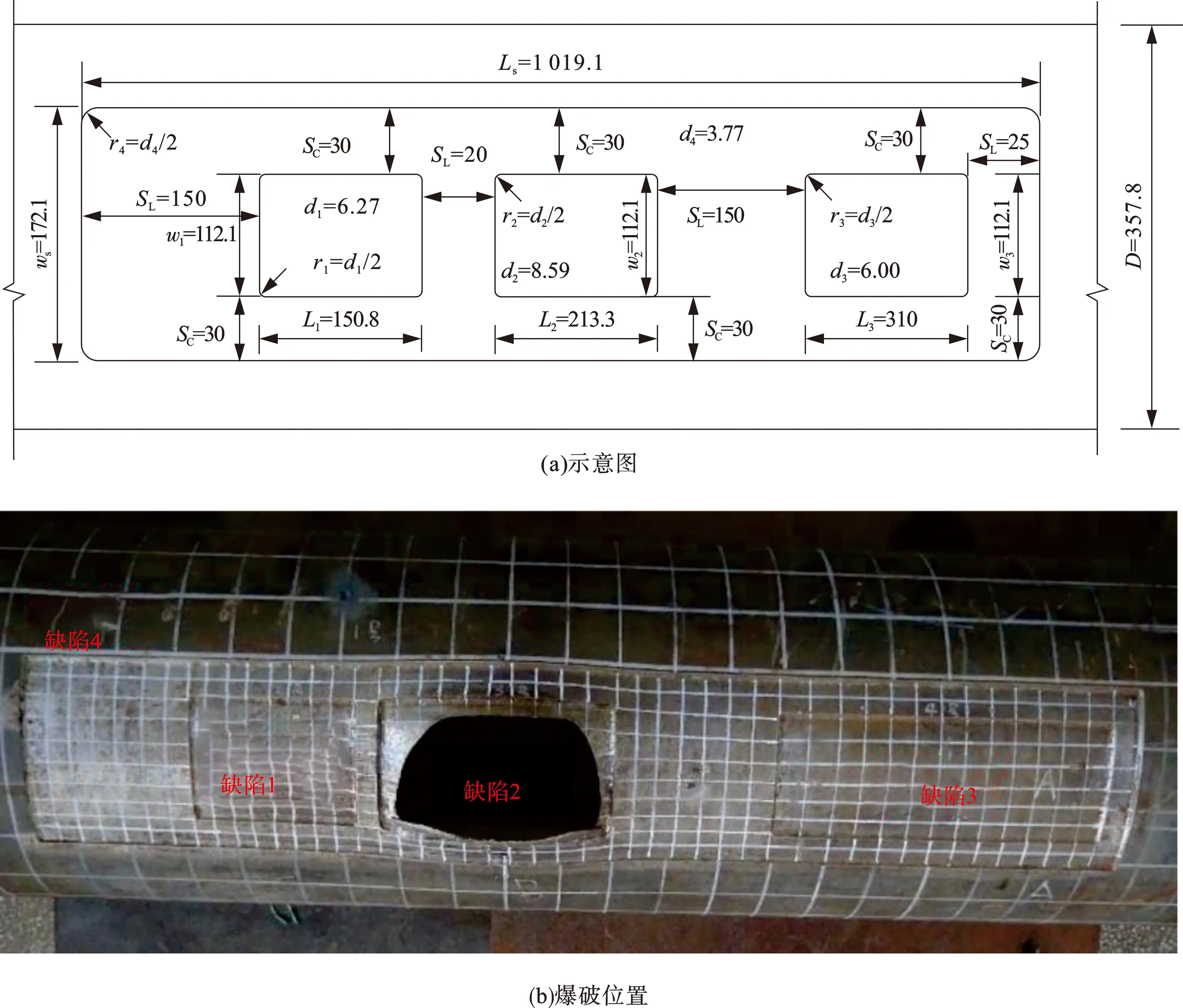
图8 不规则缺陷示意图及爆破位置Fig.8 Schematic diagram of irregular-shaped defects and burst position

表7 不同评估方法平均误差Table 7 Average error of different evaluation method
6 结 论
(1)相对于规则腐蚀缺陷的失效压力取决于最大腐蚀深度和长度,不规则腐蚀缺陷的失效压力取决于缺陷腐蚀最大深度和腐蚀深度轮廓;深浅腐蚀坑的相对深度和相对长度的增加会造成不规则缺陷失效压力降低,相对宽度对失效压力基本无影响。
(3)针对不规则腐蚀缺陷的失效压力评估,二级评估方法相对于一级评估方法更为准确,其中DNV(不规则形状)方法预测结果更为稳定,波动性更小。
(4)基于不规则缺陷的长度和轴向投影面积,提出新的不规则缺陷失效压力评估方法的平均误差相比其他评估方法降低了3.63%~39.94%,且不需要对不规则缺陷进行多次分段或分层评估,操作更为简洁高效。
