一种基于拉格朗日乘子的空间域差分系数优化方法
2022-09-05黄建平娄璐烽彭炜颋李庆洋
黄建平,娄璐烽,彭炜颋,李庆洋
(1.中国石油大学(华东)地球科学与技术学院,山东青岛 266580;2.海洋国家实验室海洋矿产资源评价与探测技术功能实验室,山东青岛 266071;3.中国石化中原油田分公司物探研究院,河南濮阳 457001)
由于差分离散,有限差分法在数值模拟过程中会出现明显数值频散[1-2],影响地震波场模拟精度[3-4],差分系数优化是压制地震波场数值频散的有效策略。差分系数优化通过调整网格点上的差分系数重新分配“权重”,能更为准确地从当前时刻波场值计算下一时刻地震波场,在不增加计算量的情况下降低数值频散[5],提高地震波场数值模拟精度[6-8]。根据实现方式的差异,差分系数优化方法分为窗函数和最优化方法,前者通过寻找合适的窗函数来快速求取差分系数,后者则是引入最优化策略计算差分系数。用于差分系数优化的窗函数法包括海宁窗、高斯窗、可缩放二项式窗、Chebyshev窗等,它将伪谱法的卷积级数截断得到窗算子来代替差分系数。早期,Zhou[9]和Igel[10]等分别使用海宁窗和高斯窗截断得到窗算子,以获得更高精度的模拟波场;随后,Chu和Stoffa[11]提出缩放二项式窗,得到旁瓣衰减迅速的差分系数,提高了计算稳定性。Chebyshev窗亦可单独用于窗算子设计,王之洋等[12]提出一种Chebyshev自褶积组合窗,通过调节纹波率、自褶积次数、加权系数3个参数,能够直观调节窗形态,改变差分系数精度。鉴于不同窗算子的特性差异,有学者设计组合窗算子[13-15],Wang等[16]在缩放二项式窗基础上提出余弦调制二项式窗,将海宁窗、Chebyshev窗、缩放二项式窗组合,通过改变调制时间和调制范围,最终获得不同的主瓣旁瓣振幅响应。也有学者通过优化方法来提升窗算子精度,Ren等[17]采用最小二乘优化方法迭代求取更高精度的差分系数。最优化策略的差分系数优化方法主要包括模拟退火法、雷米兹交换算法、最小二乘法等。模拟退火法优化的差分系数拥有更高的频谱覆盖范围和较小的误差限,朱遂伟等[18]采用模拟退火法将傅里叶有限差分系数中的两个系数扩展到4个,能显著提升成像效果。相较于模拟退火法,雷米兹交换算法计算效率更高,只需几次迭代就能求得高精度差分系数[19-20]。He等[21]应用此方法求解差分系数,在获得更宽频带的同时降低了计算成本,特别是对大尺度模型的误差累积减少有积极作用。最小二乘法是一种最小二范数全局优化方法,它依据频散关系的误差形式构建目标函数来求解优化的差分系数[22],与之类似的还有最大范数优化[23]、最小范数优化[24]等。其中Liu首先提出基于最小二乘法的差分系数优化方法,该方法能明显压制高波数域频散,其低阶差分系数可以取代高阶传统差分系数,基于此,Liu[25]和任志明[26]进一步发展了交错网格差分系数,Yong等[27]则发展了弹性波差分系数优化。虽然最小二乘法是差分系数优化研究的一个热点,但其低波数段误差仍然较大,存在频散误差以类似于正弦曲线的形态小范围偏离理想值的问题,无法准确逼近0误差。因此如何在保持最小二乘法宽频带的优势下,减小其低波数段频散误差,成为改进最小二乘差分系数优化方法的一个研究方向。笔者提出一种基于拉格朗日乘子的优化新方法,为保证宽频带,采用绝对误差二范数构造目标函数,同时加入绝对误差和作为约束条件,以增加目标函数稳定性并减小低波数段频散误差。
1 方法原理
1.1 最小二乘优化原理
最小二乘法差分系数优化原理从空间偏导数的差分格式入手,有限差分法的二阶空间偏导数的2M阶精度差分格式可以表示为

(1)
式中,x代表水平方向;h为空间采样间隔;p为在m网格点的波场值;cm为差分系数;c0为中心差分系数;M为差分系数长度的一半或差分阶数的一半。差分系数可以认为是不同网格点的“权重”,即如何利用当前时刻中心点及其周围网格点的波场值来计算下一时刻中心点波场值。需要指出的是,当前时刻中心点处的波场值对下一时刻该中心点的波场值影响最大,中心差分系数c0也最大,随着网格点距中心点的距离增加,这些网格点波场值的“权重”也减小,差分系数值随之变小。此外,考虑的范围趋于无穷远,将有无限个网格点波场值对下一时刻波场产生影响,即cm无穷多,此时波场计算较为准确,但计算量巨大。为此,需要寻找新的差分系数,实现有限个点对下一时刻波场相对精确估算。
将波场p表示为简谐波形式,将波数引入推导中,波场形式如下:
p(x+mh)=p0exp(ik(x+mh)).
(2)
式中,k为波数;p0为一常数。将式(2)代入式(1)可得

(3)
为得到仅包含差分系数的等式,取k=0,式(3)可以表示为

(4)
式(4)反映了不同网格点“权重”之和存在平衡状态,差分系数在一维线网格、二维面网格中皆围绕中心对称分布,网格点处波场值的累加对下一时刻中心波场值的影响需达到平衡,否则当前时刻的波场值将引起下一时刻波场值的异常突变。
将式(4)代入式(3)推导可得

(5)
令式(5)中
β=kh,
(6)
f(β)=β2,
(7)
φm(β)=2(1-cos(mβ)).
(8)
联立式(5)~(8)可得

(9)
为使kh在Nyquist频率上等价于π,β的取值范围设置为0到π,取式(9)的绝对误差二范数,即最小二乘法,构造出对变量β进行积分的误差函数E:

(10)
不同于传统泰勒展开获取差分系数的策略,最小二乘法利用误差最小化,使差分格式逼近偏导数。积分上限b代表优化波数区间,b越大,优化波数区间越大,但低波数段频散误差也相应变大,反之优化波数区间变小,能满足更小频散误差需求。需要注意的是,当b取值变小时,计算结果可能不稳定,对差分系数求解有一定影响。
对式(10)求极小,即E对cm求导数值为0,可得

(11)
式(11)展开可得
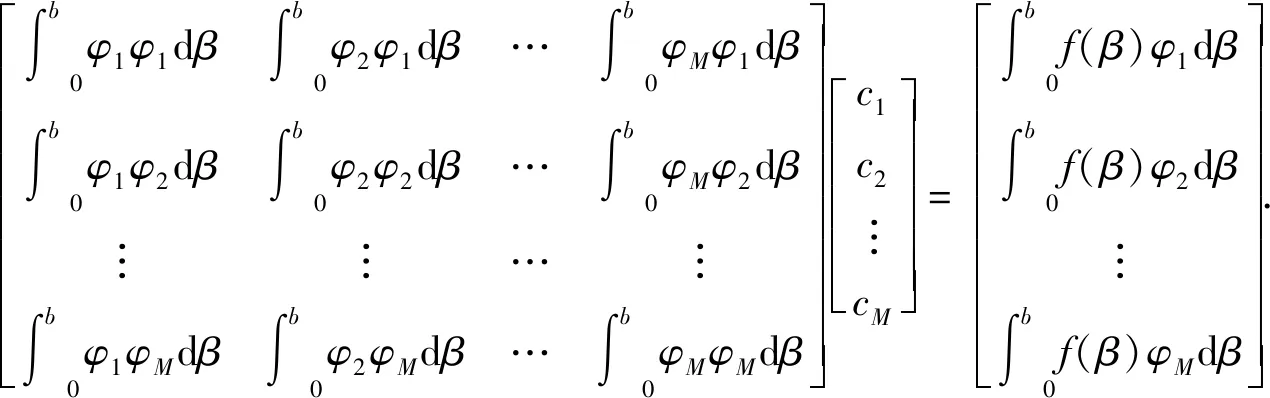
(12)
求解式(12)即可得到最小二乘法优化的差分系数。从式(12)矩阵方程可知,矩阵中的元素皆为积分形式极为复杂,前人研究证实仅由该式求取的差分系数可能出现频散误差不稳定问题。本文中新方法主要通过增加绝对误差和,引入拉格朗日乘子稳定性条件,减弱最小二乘法频散误差不稳定问题。
1.2 拉格朗日法
基于拉格朗日法的差分系数优化从空间偏导数的差分格式入手,与最小二乘法类似得到包含差分系数的等式。在误差函数的构建上,首先同时推导出绝对误差二范数及其误差和的表达式,随后构造拉格朗日函数,以绝对误差二范数为目标函数,保证差分系数宽频带,以绝对误差和为约束条件,增加目标函数稳定性,减小差分系数低波数段频散误差,最终得到包含差分系数和拉格朗日乘子的矩阵方程。该误差函数可以在保证绝对误差二范数最小的基础上通过可变参数拉格朗日乘子增加函数稳定性,约束由二范数引起的低波数段频散误差不稳定,兼顾宽频带和低频散误差的效果。
在相同阶数下,拉格朗日法与最小二乘法得到的矩阵方程矩阵元素的表达式和矩阵大小不同,拉格朗日法得到的矩阵方程的行数和列数总比最小二乘法多一行和多一列,多出的是为了求解拉格朗日乘子。
与式(3)相同推导,新方法将平面波的简谐波解代入空间导数的差分格式中,在二维情况下引入波数,得到与式(3)类似的公式:

(13)

(14)
式中,kx和kz分别为x、z方向的波数。在二维波动方程中,地震波在xz平面中传播,其振幅、传播速度等物理量都可以分解到x、z方向上,同理波数k也可以分解为kx、kz,分别为总波数在x、z方向上的投影值,θ为地震波传播方向与x轴的夹角,可得
kx=kcosθ,
(15)
kz=ksinθ.
(16)
根据最小二乘法优化差分系数的思想,首先要得到一个代表误差的量,将式(6)、(15)和(16)代入式(13)与(14),定义误差函数如下:

(17)

(18)
式中,误差函数Am(β,θ)、Bm(β,θ)分别为式(13)、(14)的绝对误差,当二者同时取极小值时,此时的差分系数cm满足在二维情况下同时减小x、z方向上的频散。若绝对误差无限逼近零,则优化的差分系数无限逼近真实空间偏导数。为简化形式,引入中间变量:
ψm(β,θ)=2(1-cos(mβcosθ)),
(19)
φm(β,θ)=2(1-cos(mβsinθ)).
(20)
为达到既保持最小二乘法频带宽的优势,又达到减小低波数段频散误差的目的,采用拉格朗日乘数法构造误差函数。误差函数φ(β,θ,λ)表达式如下:
φ(β,θ,λ)=

(21)
式中,λ为拉格朗日乘子,代表绝对误差和在误差函数中所占权重,在计算差分系数的同时λ也会计算出来。该误差函数包含传播角度θ,将波数划分为x方向和z方向,能够更好模拟声波在二维模型中的传播过程,并且充分利用两个方向的波数。其中前半部分为x方向的绝对误差二范数,继承了最小二乘法频带宽的优势,后半部分为z方向的绝对误差和,体现了新方法为约束最小二乘法在低波数段产生较大频散误差所采取的策略。前后部分都采取二重积分的形式,优化角度θ取0~2π以保证差分系数能满足所有传播方向,积分上限b取0~π,b取值越大,优化波数区间越广。
为使误差函数取极小,令误差函数φ(β,θ,λ)对差分系数cm和拉格朗日乘子λ的偏导数都为0,同时满足最小误差条件,条件表示如下:
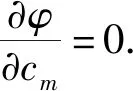
(22)
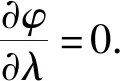
(23)
化简可得

(24)
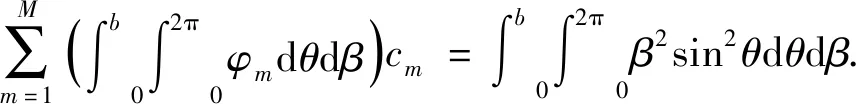
(25)
式(24)、(25)分别为满足式(22)、(23)的矩阵,式(24)包含M个等式,且同时含有M个差分系数以及拉格朗日乘子λ,式(25)仅包含M个差分系数。
将式(24)、(25)联立展开可得
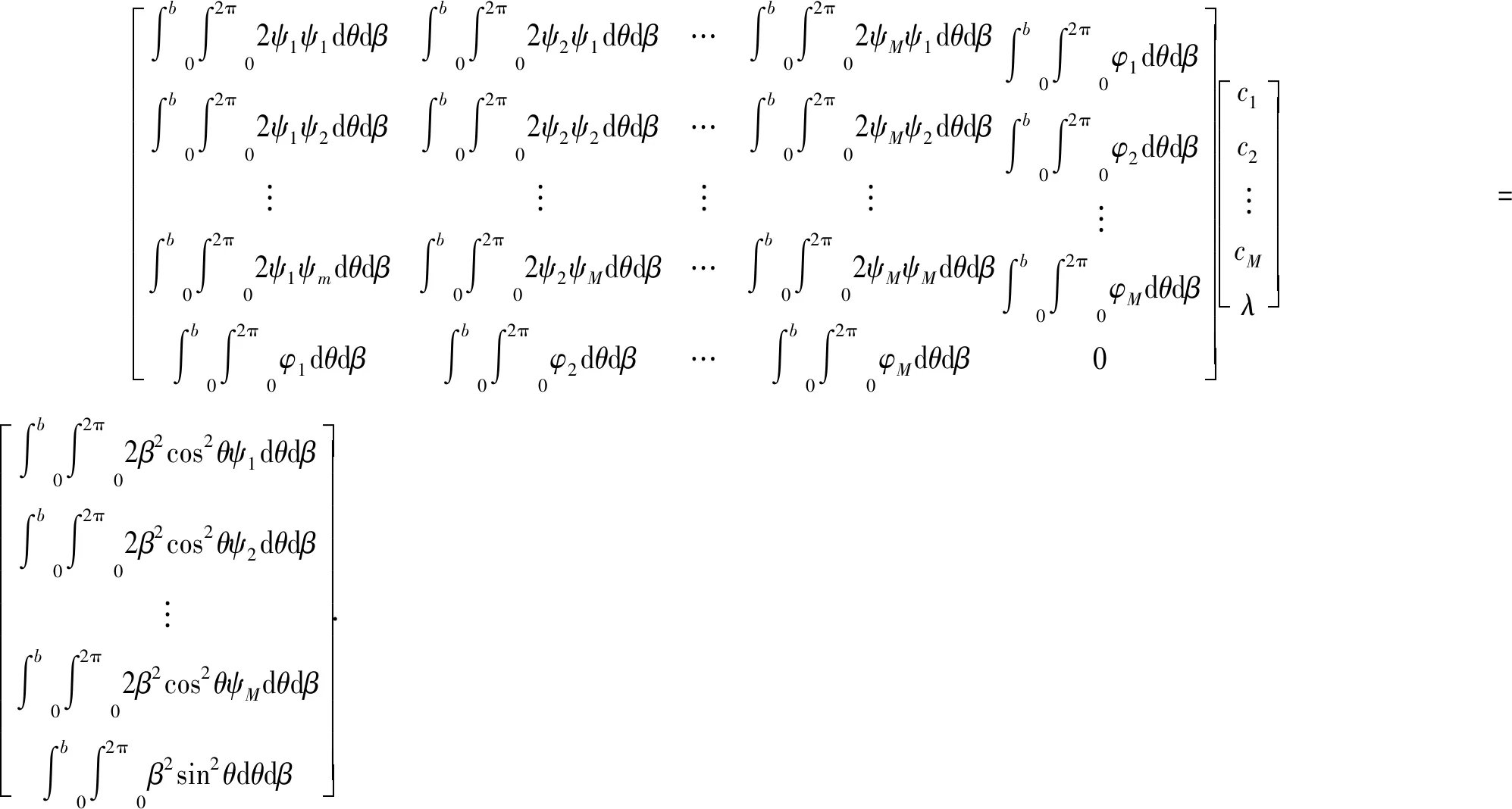
(26)
从矩阵方程中可以看到,需要求解的未知量为差分系数cm以及拉格朗日乘子λ共M+1个变量,方程最左端为(M+1)×(M+1)的方阵,右端为(M+1)×1的长方阵。求解过程发现,矩阵方程中用二重积分表达的元素值对矩阵方程求解的稳定性有重要影响。计算的差分阶数越高,矩阵方程越大,对积分精确计算的要求也越高。
表1为最小二乘法和拉格朗日法利用最小化空间域频散关系绝对误差优化差分系数的b取值,b代表优化波数区间,误差限η为1×10-4。通过限制误差限,本文中对比了两种方法在相同误差限下的b取值,表1中最小二乘法记为LSM,拉格朗日法记为Lagrange。可以看到,除M=3,其他阶数下拉格朗日法的b取值普遍比最小二乘法小,其原因可能为拉格朗日法相对于最小二乘法在低波数段的频散误差较小,但同时其有效频带宽度变小,频散误差最大值变大,为保证符合误差限要求,必须降低b值。在表1的b取值下,利用拉格朗日法计算得到不同阶数的优化差分系数,如表2所示。当M从2增加至10时,相应的拉格朗日乘子λ分别为-3.694×10-5、2.912×10-5、-1.221×10-5、1.131×10-5、-9.017×10-6、1.765×10-6、-6.347×10-6、5.175×10-6、-1.563×10-6。

表1 最小二乘法和拉格朗日法的b取值Table 1 Value of b in the least square method and Lagrange method
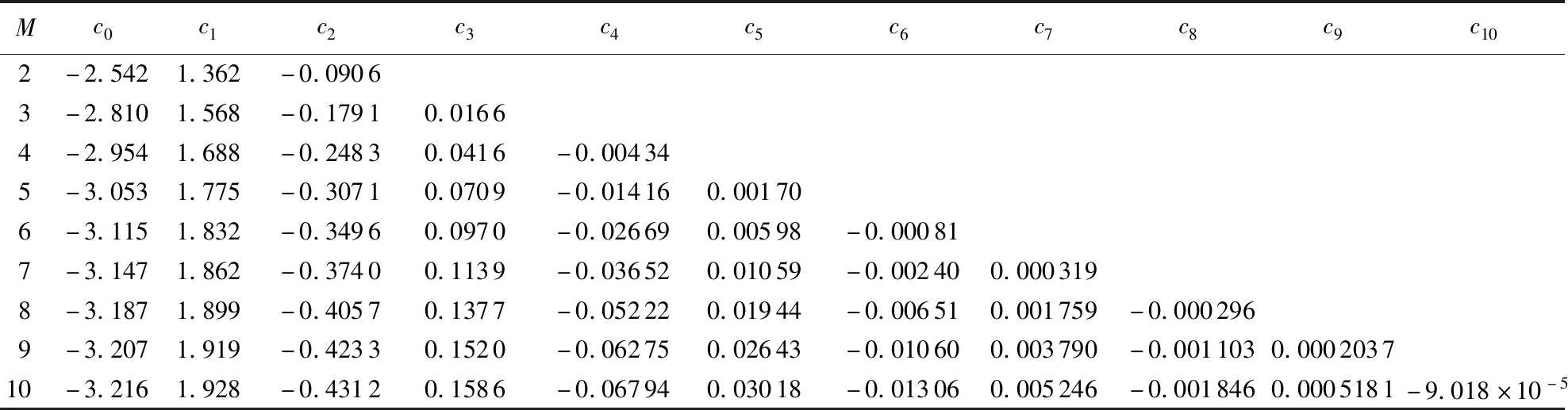
表2 拉格朗日法的优化差分系数Table 2 Optimal finite-difference coefficient of Lagrange method
2 频散测试
在正演模拟中不同地震子波具有不同主频,实际地震波更加复杂,往往覆盖多种频率,从几赫兹到几十赫兹不等[28],且炸药震源每次激发时产生的波形不尽相同,因此差分系数的有效频带宽度需较宽,即使是固定波形的激发震源,也期望差分系数在某一频段内频散误差小。由此,差分系数优化须同时追求宽频带和低频散误差,本文的目标就是在保持最小二乘法宽频带的基础上,进一步减小其低波数段频散误差。
采用绝对误差ε进行频散分析,在频散曲线中,ε等于0时,数值模拟无空间频散,ε偏离0越大,频散误差越大,在正演模拟中空间频散越明显。
为对比最小二乘法和新方法的频散误差大小,本文中以kh为横轴,绝对误差ε为纵轴,作图1所示最小二乘法与新方法优化的差分系数在不同阶数下的绝对误差频散分析图。误差限皆为1×10-4,重点关注低波数段。图1中,虚线表示误差限,以限制最大频散误差值,并调整参数b使两条频散曲线的最大频散误差一致,便于比较二者在相同误差限下的频散误差大小。通过图1可以看到,在低波数段,粉色曲线明显更靠近零值,曲线更加平缓,说明新方法频散误差比最小二乘法小,随着波数变大,两条曲线渐趋一致,达到误差限之后快速下降,频散误差急速增大,新方法比最小二乘法更快超出误差限,说明新方法的有效频带宽度较小。
综上可以看出:①在相同误差限下,新方法优化的差分系数在有效频带宽度内的频散误差小于最小二乘法;②新方法对低阶和高阶差分系数都有优化作用,都能减小频散误差,在阶数较低时,如M=3、5,优化效果好,阶数较高时,如M=8,优化效果减弱;③在低波数段,新方法的优化效果更加明显,减小频散误差效果最好,随着波数变大,效果减弱;④新方法的有效频带宽度较小,但与最小二乘法差距很小。频散分析证明,本文方法不但继承了最小二乘法宽频带的优点,同时减小了低波数段频散误差,在低阶、低波数段的频散压制效果好。

图1 最小二乘法与新方法的频散分析图Fig.1 Dispersion analysis of least square method and new method
由于最小二乘法缺少限制条件约束,也没有使用一范数模型作为目标函数,导致其在有效频带宽度展宽的同时低波数段频散误差增加。新方法能够改善这一问题,其原因在于新方法采用拉格朗日乘数法构造误差函数,该误差函数包含绝对误差二范数,能够扩宽有效频带,且增加了绝对误差和,能增强误差函数稳定性,在频散曲线中体现为低波数段频散误差的减小。如Miao等[24]提出的一种基于一范数构造目标函数的差分系数优化方法,能减小误差累积,增加方法稳定性。由于本文中将两种方法的误差限调整一致,因此新方法在低波数段频散误差减小明显,随后两种方法渐趋一致。差分阶数较低时,新方法减小低波数段频散误差的效果明显(图1(a)、(b))。随着阶数升高,最小二乘法精度提升,因此新方法在高阶时减小频散误差的效果减弱(图1(d))。新方法也为减小频散误差牺牲了部分有效频带宽度。
图2为传统方法与新方法优化的差分系数在不同差分阶数下的绝对误差频散分析。在差分阶数选取上,分别选取10阶新方法,10、16、24阶传统方法进行对比。首先观察4条曲线在全波数域的频散误差,可以发现kh在1.5~3之间,传统方法的绝对误差频散曲线随波数增大而增大,图中黑色曲线整体高于红色曲线,新方法优于同阶数传统方法,且与16阶传统方法相当。为观察频散曲线前部的微小变化,重点放大kh在0~2之间的区域,且只显示频散误差在±2×10-4之间的曲线。可以看到,新方法有效频带更宽,具体表现为新方法有效频带宽度比传统方法10、16阶广,可与24阶比拟,同时,新方法的低波数段频散误差大于传统方法,频散曲线在给定的误差范围内振荡较快,以类似于正弦函数的形态小范围偏离理想值,无法准确达到0误差,传统方法则表现为一段0直线。
分析说明:①新方法具有宽频带优势,能极大扩宽有效频带,低阶新方法可以达到高阶传统方法的有效频带宽度;②在低波数段,新方法频散误差大于传统方法,可能是因为优化的差分系数具有更宽的有效频带宽度,但代价是在有效频带宽度内分布有更大的误差,通过大量模型和参数测试,这些误差都在可以接受的范围。该结果同样由新方法误差函数的构造导致,新方法的目标函数为绝对误差二范数,其获得的最小二乘解不是零误差,而是在“二范数最小”意义下达到的残差最小。因此与最小二乘法类似,能够极大展宽有效频带,同时低波数段频散误差较大。
在测试过程中,随着阶数升高,本文方法也存在一定不稳定性,随着参数b减小,新方法的最大频散误差、低波数段频散误差、有效频带宽度同步减小,但发现部分异常现象:①在某些较小的b值上,新方法符合误差限,同时低波数段频散误差减小非常明显,如M=5,b=1.56时,M=6,b=1.87时;②b小于一定值时频散曲线不稳定,b的微小变化可能引起曲线剧烈变化,如M=5,b<1.55时,M=6,b<1.70时,M=7,b<2.02时,M=8,b,2.25时;③在某些b值上,新方法频散误差突然变大,如M=6,b=2.04时,M=7,b=2.15时,M=8,b=2.265时,M=9,b=2.39时;④差分阶数较大时,随着b减小,最大频散误差不减小,如M=7,b>2.10时。总体而言,新方法在低阶时很稳定,随着阶数升高,逐渐不稳定,频散曲线更容易随b减小发生突变,如M>6时。究其原因,可能是随着矩阵阶数升高,矩阵稳定性变差,导致求解变得困难,且矩阵元素皆为积分形式,积分上限b的微小变化能够影响整个矩阵,特别是b值较小时高阶系数的求解。当优化波数范围较小时可能存在不稳定,可将正则化算子[29]引入系数求取过程,雍鹏等[30]采用牛顿法快速求解优化差分系数。

图2 传统方法与新方法的频散分析Fig.2 Dispersion analysis of traditional method and new method
3 模型试算
3.1 均匀模型
考虑到研究重点为低波数段,取模型网格点数为200×200,模型速度为1 500 m/s,震源位于模型中心,计算主频为30 Hz的雷克子波,空间采样间隔5 m,时间采样间隔0.1 ms,以保证数值频散以空间频散为主,时间频散几乎不出现。
为便于对比3种方法数值模拟的差异,采用四宫格形式展示波场快照计算结果,每个宫格对应一种情况,同时对应给出波场残差图以比较不同方法的模拟精度和稳定性。图3为传统方法、最小二乘法、新方法分别在传播时间t=0.3,1.6 s时的均匀模型波场快照以及波场快照残差对比,其中图3(a)、(c)为波场快照对比,图3(b)、(d)为波场快照残差对比,参考波场采用50阶传统方法(可视为精确解)。沿逆时针方向,左上角编号1采用8阶传统方法,左下角编号2采用8阶最小二乘法,右下角编号3采用8阶新方法,右上角编号4采用12阶传统方法,由此,3种方法可依次循环对比。
对比图3(b)发现,低阶传统方法的残差表现为黑白交替的深色条带状,残差值大,最小二乘法的残差表现为边缘模糊的带状,中部残差值最大,且在部分区域残差覆盖范围扩大,新方法则能改进这一问题,残差值明显减小,残差覆盖范围缩小,最接近于高阶传统方法模拟精度,在图3(d)箭头与红框所示处同样能观察到频散依次改善的情况。计算结果表明在相同阶数下,新方法的空间频散比传统方法和最小二乘法小,波场快照残差更小,模拟精度更高,低阶新方法可以替代高阶传统方法的模拟精度。这与频散分析中新方法宽频带且低波数段频散误差小的结论相符,新方法有效频带宽度比传统方法宽,因此残差小于传统方法,低波数段频散误差比最小二乘法小,因此残差小于最小二乘法,能量更加集中于反射波主波形上,减小能量分散。
为精细对比波场快照残差图,抽取单道进行分析。图4为3种方法不同阶数在不同传播时刻的单道残差对比分析,图4(a)、(b)分别来自图3(b)、(d)500 m处的单道记录。由下到上依次绘制8阶传统方法、最小二乘法、新方法和12阶传统方法,并绘制参考道单道残差(值为零),用以量化3种方法的残差值。在图中相同深度处选点测量残差值,选段测量残差覆盖范围,进行数值标注。
图4(a)中,低阶传统方法的残差曲线变化幅度最剧烈,呈明显的锯齿形,而同阶最小二乘法和新方法的残差曲线变化幅度小,较平滑,且新方法残差值明显比最小二乘法小。在图4(b)中,同阶数时新方法残差曲线最平缓、残差值最小,特别是在中部深度520 m处,优化效果显著,而深度750 m处新方法残差值最小,即频散最小。从残差覆盖范围的测量中也可以证实新方法能够减小残差覆盖范围。
简单模型测试结果表明,新方法地震波场快照残差小于最小二乘法,同时约束了残差覆盖范围。在同阶数下,新方法的频散小于传统方法和最小二乘法,证明了新方法能够在明显减小传统方法频散的优势上进一步降低最小二乘法频散的结论,能够实现更高的数值模拟精度。
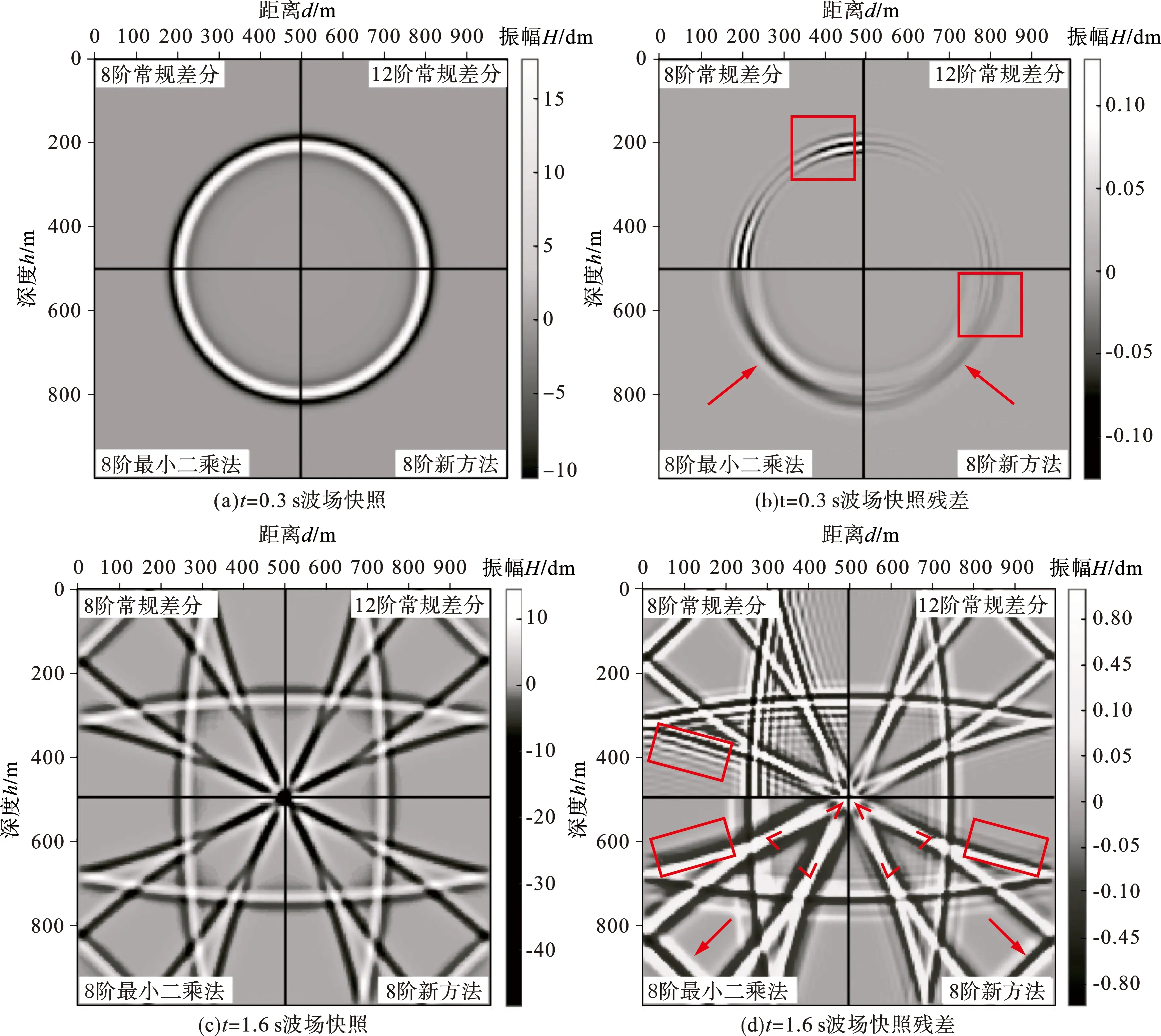
图3 不同方法的波场快照和残差对比Fig.3 Comparison of snapshots and residuals of snapshots of different methods
3.2 Marmousi模型
为验证新方法对复杂模型的适应性,采用SEG提供的国际Marmousi模型进行正演模拟,模型网格点数为1 360×700,震源位于表面中心,计算主频为30 Hz的雷克子波,空间采样间隔5 m,时间采样间隔0.1 ms,地震波场模拟时间2.0 s。
图5为最小二乘法、新方法在传播时间t=2.0 s时的Marmousi模型波场快照和波场快照残差对比。其中图5(a)为波场快照对比,图5(b)为波场快照残差对比,参考波场采用50阶传统方法。为使对比直观,采取左右对比的方式,左、右上方分别为8阶最小二乘法、新方法,左、右下方分别为16阶最小二乘法、新方法。
图5(a)中模拟波场非常复杂,外围波前面能量最强但无规则弯曲,内部存在众多反射波形,波形混叠难以分辨,左下角存在明显浅色区域,可能是模型构造复杂、存在速度异常体导致。通过图5(a)无法分辨出两种方法的频散大小,因此重点对比波场快照残差,可以看出,在相同阶数下新方法波场快照残差小于最小二乘法,在箭头所指波前面处和红框所示内部区域处残差明显减小。说明低阶新方法优化效果好,8阶新方法的模拟精度高于16阶最小二乘法,但高阶新方法优化效果减弱,应用效果不显著。Marmousi模型正演表明,新方法在复杂模型中同样能够减小频散,将地震波能量集中于波前面上,提升模拟精度。
为更加精细对比两种方法的波场快照情况,抽取单道进行分析。图6为两种方法不同阶数的单道残差对比分析,其中,图6(a)、(b)分别为图5(b)中3 000、5 000 m处的单道残差。将4条残差曲线按阶数分为两组进行对比,下方蓝色组、上方红色组分别为8阶和16阶最小二乘法和新方法。按组对比可见,新方法残差曲线总体上较最小二乘法平缓,尤其是蓝色低阶方法,具体表现为波峰波谷残差值明显减小,曲线整体更靠近零值,从标记的数值点上可见,蓝色低阶时残差值减小60%以上,红色高阶时残差值减小40%以上,新方法减小数值频散的效果优于最小二乘法。综上所述,新方法对于复杂模型也具有较好适应性,在低阶、高阶时都能提高数值模拟精度,低阶时改善效果明显,随着阶数升高改善效果减弱。Marmousi模型单道残差分析同样证明新方法压制数值频散的效果优于最小二乘法。

图4 不同方法的单道残差对比Fig.4 Comparison of single-channel residuals of different methods

图5 Marmousi模型的波场快照和残差对比Fig.5 Comparison of snapshots and residuals of snapshots of Marmousi model
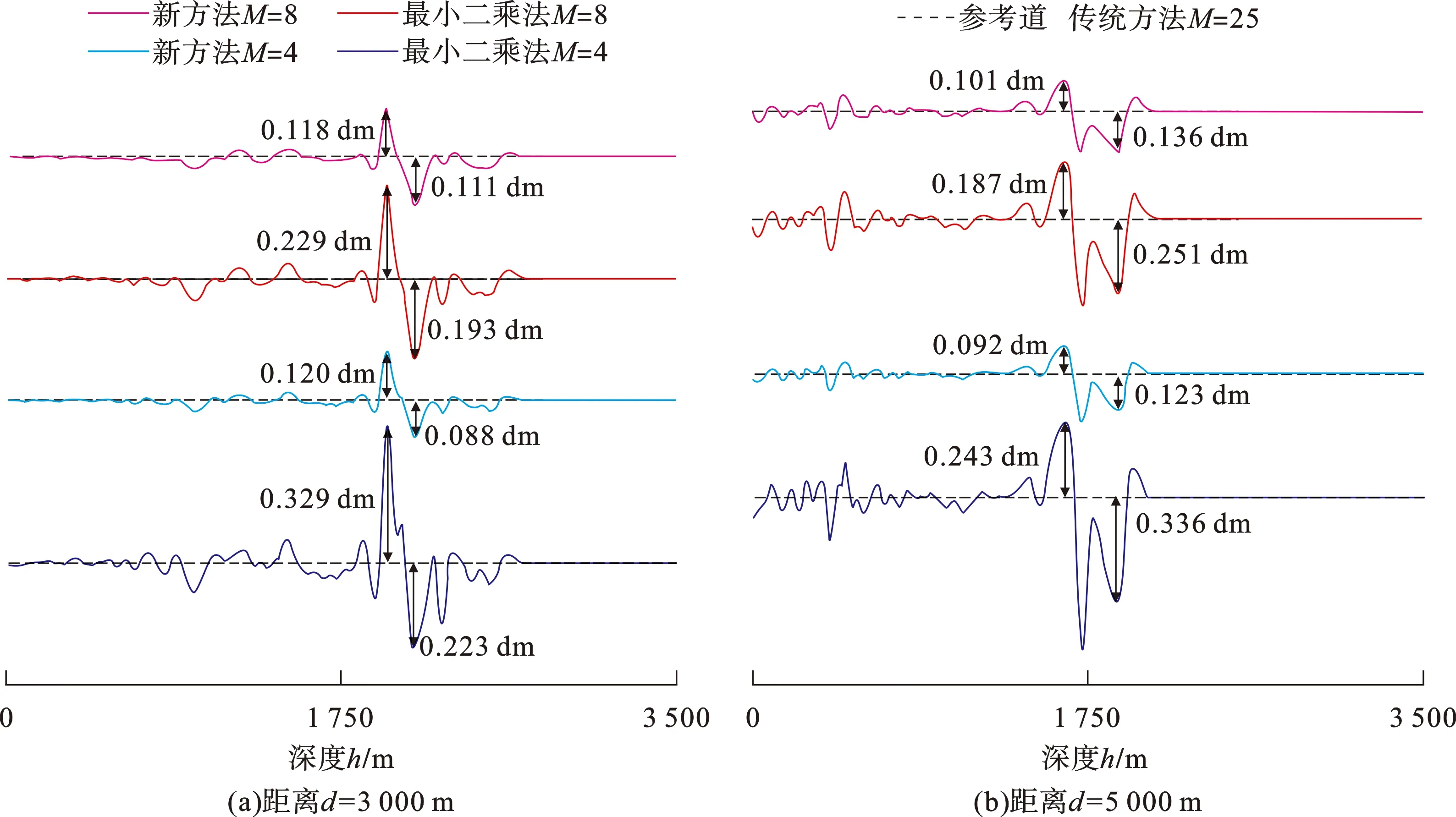
图6 两种方法的单道残差对比Fig.6 Comparison of single-channel residuals of two methods
4 结束语
针对最小二乘差分系数优化法在低波数段频散误差大的问题,在采用绝对误差二范数的同时,有效利用误差和约束频散误差,构造拉格朗日函数求解差分系数,提出了一种基于拉格朗日乘子的空间域差分系数优化新方法。均匀模型和Marmousi模型测试结果表明:新方法的低波数段频散误差小于最小二乘法,低阶、低波数时优化效果明显,阶数升高效果减弱,且相比传统方法,新方法的有效频带更宽;新方法能够减小波场残差同时缩小残差覆盖范围,同时其数值频散也优于最小二乘法,能在一定程度上提高地震波场模拟精度;新方法对复杂模型适应性较好,能在压制数值频散的同时集中波前面能量,减少地震波能量分散从而提升模拟精度。
