基于U-net卷积神经网络图像分割的波浪测量方法❋

任志伟， 陈松贵， 王收军， 王佳伟，2

(1. 天津理工大学机电工程国家级实验教学示范中心， 天津 300384； 2. 交通运输部天津水运工程科学研究院 港口水工建筑技术国家工程实验室， 天津 300456)

充分认识和了解波浪要素是人类进行海洋与海岸水动力基础研究的必要条件，而波高和周期作为重要的波要素，紧密关联着海岸工程的建设，因此其测量方法和测量精度值得研究。传统的实验室波高测量方法主要包括两类：一是利用各类波高传感器等仪器类装置与水体直接接触测量；二是利用图像处理手段针对视频间接测量。上述测量方法优、缺点：电容式波高传感器通过电容值测量波高，然而，电荷数却容易受电磁场环境干扰，致使传感装置采样稳定性下降[1]；基于加速度计和陀螺仪结合的方法通过采集载体运动信息，利用姿态矩阵将陀螺仪输出的姿态角信息转换到地理坐标系并进行处理，去除原始加速度信号中的毛刺和直流分量后再对加速度信号进行二次积分[2]，进而求出波高，但是每次进行积分过程时受仪器温度变化和工作环境等因素的影响会产生趋势项，从而影响测量结果的精度；超声波测距仪依据声波传递速度和发送与接收声波的时间差值计算液位高度，但是超声波在不同密度、压力、温度和浓度的传播介质中传递速度都不相同[3]；基于光学的测量方法实现了非接触式的测量[4]，避免了因电子传感装置与水体的直接接触而导致的测量误差，但在强烈光照的工况下摄像机对波面的识别会受到影响；针对视频图像利用阈值分割的途径也实现了非接触式的测量，可通过测出水位值间接计算波高，但其不能分割光照强烈的视频图像，因而具有局限性；BP神经网络算法可用于波高的测量，但在对水位高度的预测中数值稳定性表现较差[5]；基于快速视觉的波高测量方法是用摄像机拍摄波浪运动过程，通过灰度化等图像处理手段统计白色像素点数量[6]，从而计算波高，但受其测量原理影响需向液体中添加蓝色染料来突出水体，限制性很大。图像处理中传统的图像分割方法主要有3种：基于阈值的分割方法、基于区域的分割方法和基于边缘检测的分割方法[7]。上述3种分割方式均存在着自身局限性。如阈值分割不考虑空间特征，因此对噪声比较敏感，鲁棒性不高；区域分割中的区域生长法计算缓慢且对噪声较敏感，分裂合并法可能会破坏区域边界；边缘检测不能保证边缘的连续性和封闭性，对于较高细节区域的处理存在不足，容易产生碎边缘[8-9]。

近年来随着计算机技术的快速发展，基于深度学习的图像分割成为了图像处理中更加高效的方法，FCN、Seg-net、PSP-net和U-net等卷积神经网络通过对已有图像数据的学习，可实现高品质的分割，其中U-net因其网络结构和编解码特点相较于其他3种网络的表现更加出色，在此背景下，本文利用U-net卷积神经网络对波浪运动视频进行图像分割，进而测量波高和周期。本文主要包括以下几部分：第一部分介绍了U-net卷积神经网络的研究方法；第二部分将测量结果与波高传感器进行比较分析；第三部分进行了本研究方法的适用性分析；第四部分对研究结果进行了总结和展望。

1 U-net卷积神经网络

1.1 基本原理

U-net卷积神经网络是建立在全卷积神经网络的基础上，实质上属于编码-解码模型[10-11]，网络架构如图1所示，整个网络结构由收缩路径(见图1左侧部分)和扩展路径(见图1右侧部分)2部分组成，其中收缩路径即是编码过程，也叫下采样过程，扩展路径即是解码过程，也叫上采样过程。在编码过程中，每一次下采样操作都通过2次same卷积进行图像的特征提取，所用的卷积核尺寸为3×3×3，卷积后通过ReLU激活函数进行激活，之后接一个2×2的最大池化操作扩大全局感受视野并对特征进行压缩及下采样操作，每一步下采样时特征通道数量加倍，特征图尺寸减小到之前的一半,4次下采样后开始进行编码阶段的上采样，每次上采样进行反卷积操作会使特征通道数量减少到之前的一半，特征图尺寸为前一次上采样的2倍，结构中特征图尺寸如卷积块体(蓝色矩形)左下角数字所示，特征通道数量如卷积块(蓝色矩形)上端数字所示。最后通过1个1×1的卷积核将特征通道的数量降为所需数量，并用sigmoid激活函数进行预测分类[12]。网络的关键在于将编码与解码过程之间的跳跃层进行了特征融合，减少了在编码过程中进行的最大池化操作所导致的底层特征信息的丢失，从而得到高品质的分割结果。

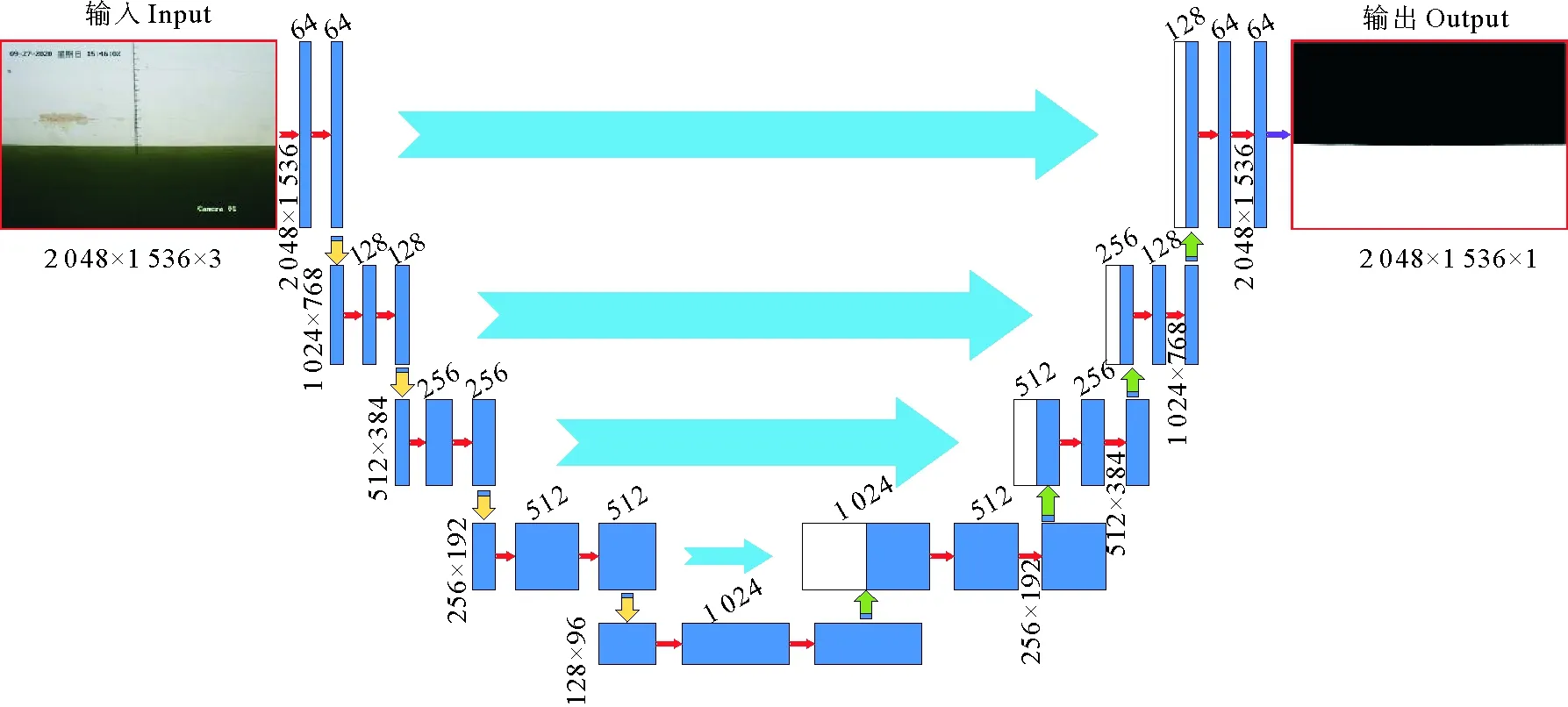
(图中红色箭头是指用3×3×3的same卷积核和Relu激活函数进行卷积与激活处理，黄色箭头是下采样操作中采取的最大池化操作，绿色箭头为上采样过程中反卷积处理，紫色箭头是指通道降维和类别输出。The red arrow in the figure refers to the convolution and activation processing with the 3×3×3 same convolution kernel and Relu activation function. The yellow arrow is the maximum pooling operation taken in the downsampling operation, and the green arrow is the deconvolution processing in the upsampling process. The purple arrow refers to channel dimensionality reduction and category output.)

1.2 数据集来源及预处理

数据主要来源于大比尺波浪水槽中的模型实验。实验布置如图2所示，大水槽全长450 m、宽5 m、高8～12 m，水槽一端装设造波机，最大造波能力下的波高为3.5 m，造波周期为2～10 s，可以模拟真实海洋中的波浪，内置4个波高传感器来测量波高，传感器量程为5 m，测量精度1%，并在水槽一侧的墙壁顶端每隔7 m装设1个高清摄像机，共装8个，摄像机和波高传感器采集帧率都为25 帧/s,且二者位置都与摄像机对齐，摄像机镜头视角可以完全覆盖对面波浪的运动，为避免标尺体积对实验造成影响，所用标尺为水槽墙壁上喷涂的刻度尺，其分辨率为2 cm。本文针对表1所示的9种工况进行实验并将录制的视频存储到计算机，按帧制作成时间连续的2 048×1 536的高清照片并用张氏标定法[13]进行畸变矫正处理。

表1 实验工况参数表

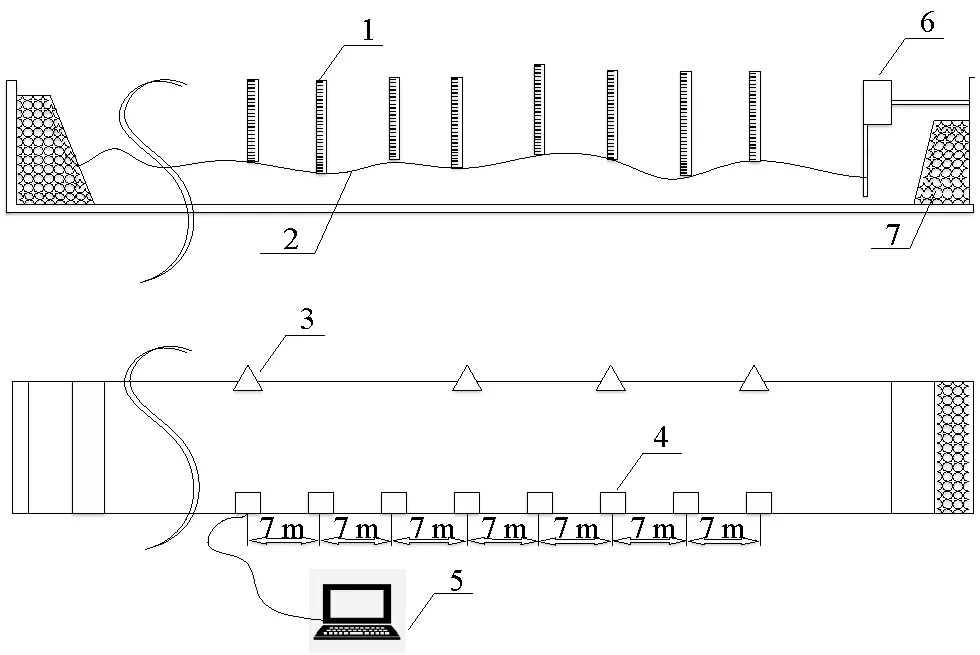
(1.刻度尺Scale; 2.水位线Water level line; 3.波高传感器Wave height sensor; 4.摄像机Camera; 5.计算机处理系统Computer processing system; 6.造波机Wave maker; 7.消波材料Wave-absorbing material.)

通过python中的labelme工具对获取的波面图像进行标签集制作，制作标签如图3(b)所示，其中黑色代表原图中墙壁，白色代表水体区域。

深度学习中的数据集数量对神经网络模型优良程度有着很大的影响，过少的数据集训练易产生过拟合现象[14]，现有数据集可通过旋转、平移、镜像等数据增强方式进行扩充[15]，本文采用图像镜像的方式对数据样本进行数据扩增，结果如图3所示，得到波面原图和标签集的镜像图片。

图3 数据增广结果

1.3 模型训练

在大比尺波浪水槽实验中采集了1 200张波面图像，经对原始波面图像进行数据增广后，数据集增加为原来的2倍，随机选择其中80%的数据当作训练集，另外20%作为验证集，训练次数(Epoch)50次，模型训练1次迭代所使用的样本量(Batch size)设置为2。训练U-net神经网络模型的条件如表2所示。

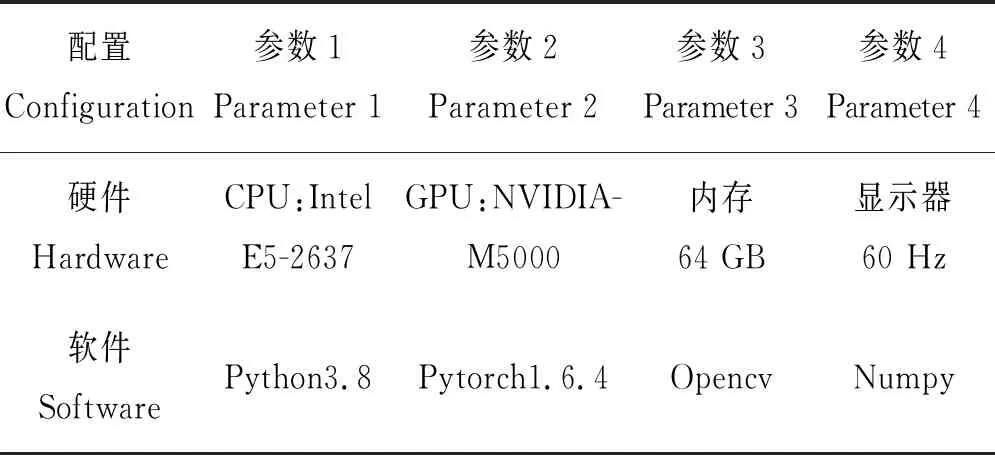
表2 模型训练条件

1.4 损失函数

由于本实验实质上进行的是水体和背景的二分类问题，在二分类的情况下，模型最后需要预测的结果只有2种情况，对于每个类别本研究预测得到的概率为p和1-p，因此本文所用模型的损失函数选取为交叉熵损失函数：

(1)

式中:N表示样本总数；yi表示样本i的标签,正类为1，负类为0；pi表示样本i预测为正的概率。训练时的损失值曲线变化如图4所示，验证集数据的损失值最终降为0.01以下。

(图中黑线为训练过程中数据，红线为验证过程中数据。The black line in the figure is the data during the training process, and the red line is the data during the verification process.)

1.5 模型评价指标

本文所用U-net卷积神经网络模型的评价指标为交并比(Intersection over Union，IoU)和正确率(Accuracy)。IoU是一个专用于评估分割性能的指标,计算公式如：

(2)

式中：A为真实标签；B为实际分割结果。

正确率(Accuracy)是评价分割结果正确性的评价指标，正确率越高，分类器越好。

(3)

式中：TP为神经网络正确划分正例的个数；TN为神经网络正确划分负例的个数；P为正例总数；N为负例总数[16]。由表3可知，数据增广方式进一步提升了模型的分割精度。

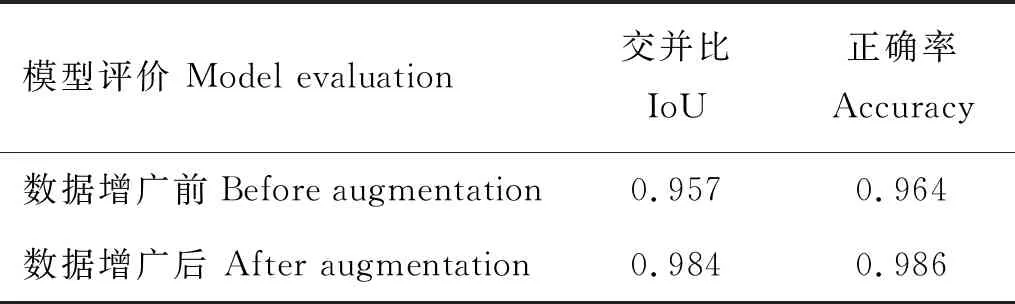
表3 数据增广前后模型指标

2 实验结果及分析

2.1 分割结果的映射检测

本文用训练好的U-net卷积神经网络对表1所示的9种工况波面图进行图像分割，得到图5(a)所示的分割结果及水位线数据信息，其中，水位线的数据信息是对每张图像分割结果以列为单位，自上而下遍布所有像素点，当扫描到白色像素点时记录其高度位置信息，从而得到每张图像的水位信息，将分割结果的水位线数据映射到原图中检测分割结果的精度，可见分割结果的水位能够与原图水位重合,如图5(b)所示。

图5 分割结果

2.2 光照波面的测量结果

实验对波高和周期要素的测量关键在于对波面图像的分割，本文所利用的U-net卷积神经网络克服了光照波面对阈值分割测量法的影响，不会受到光照工况下的限制，相对具有更广泛的使用空间，二者对光照波面的分割如图6所示，其中阈值分割结果并不理想，这主要是因为当波面受到不均匀的光照影响时，水体局部区域的颜色与墙壁相近(见图6(a))，阈值分割结果如图6(c)所示，黑色表水体，白色代表墙体，因为阈值法无法准确的判断其前景和背景，易将强光照射部分的水体错误识别成墙体，所以部分光照区域的水体被分割成白色，此现象在光照强烈区域表现尤为明显，而U-net卷积神经网络在训练的过程中可以对图像的颜色、亮度等元素进行学习，从而可准确的实现对光照波面的图像分割，分割效果如图6(b)所示，其中，黑色代表墙体，白色代表水体。

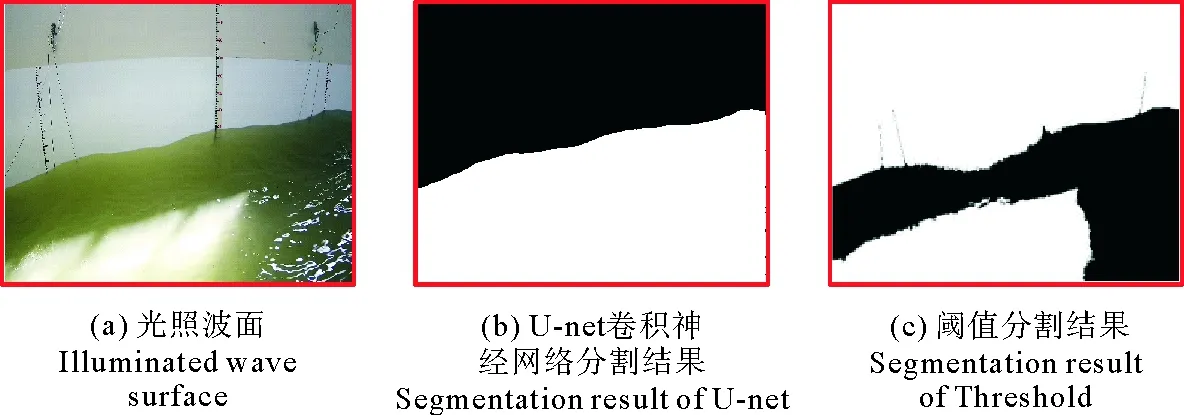
图6 两种图像分割法对光照波面的分割结果

2.3 波高计算

对原波面图像上的标尺每10 cm拾取一个像素点记录高度信息，并将像素点高度与标尺上的实际刻度相对应，拟合像素高度和标尺实际高度的转换关系。利用该转换关系即可完成水位线数据从像素高度到实际高度的转换。提取每张图像标尺处的水位值，即可观测水位的变化过程，继而通过上跨零点法计算波高。

实验针对表1所示的9种工况，用U-net卷积神经网络、波高传感器及像素识别3种方式进行波形比较，其中，像素识别是通过手动对每一帧波面图片识别水位高度，识别分辨率计算方法为

(4)

式中：Cy表示每个像素点代表的实际距离；Ymax表示垂直方向像素坐标最大值表示的实际高度；Ymin表示垂直方向像素坐标最小值表示的实际距离；Ny表示垂直方向像素点数量。计算表明像素识别分辨率可达2 mm/pixel，相较于传感器的厘米级测量精度更精确，依靠人力手动识别每张波面图像水位过程繁琐耗时，不具实际应用性，但测量结果可靠，因此可作为测量结果的基准值来比较U-net卷积神经网络的波浪测量方法的精度和波高传感器的精度。观察图7可发现3种测量方法测得规则波和不规则波的波形曲线吻合度都较为一致，但在波峰处可发现U-net卷积神经网络测得的波高值和像素识别测量的更为接近，而传感器测量的值相对偏大，这主要是由于波浪回落过程中形成的“挂水”现象导致的。

(图中黑线为神经网络所测波高，红线为波高传感器所测波高，蓝线为像素识别的波高。In the figure, the black line is the wave height measured by the neural network, the red line is the wave height measured by the wave height sensor, and the blue line is the wave height identified by the pixel.)

2.4 计算结果与分析

本文以像素识别结果为基准，针对规则波和JONSWAP谱不规则波各120个波高分别计算U-net卷积神经网络和传感器测量的波高与周期的相对误差，计算公式为:

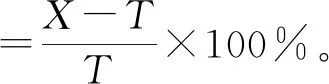
(5)

式中：X指U-net卷积神经网络或传感器的测定值；T指以像素识别为基准的真实值。计算结果如图8(a)所示，U-net卷积神经网络测量结果的误差均小于传感器，其中1～6组为规则波测量结果，U-net卷积神经网络计算的误差最大为2.25%、最小为1.72%，传感器的误差最大为4.15%、最小为2.06%，7～9组不规则波中U-net卷积神经网络计算的误差最大为2.3%、最小为1.45%，而传感器最大误差为4.1%、最小为1.8%，可见，基于U-net卷积神经网络的波浪测量方法的测量精度比波高传感器的测量精度更高。

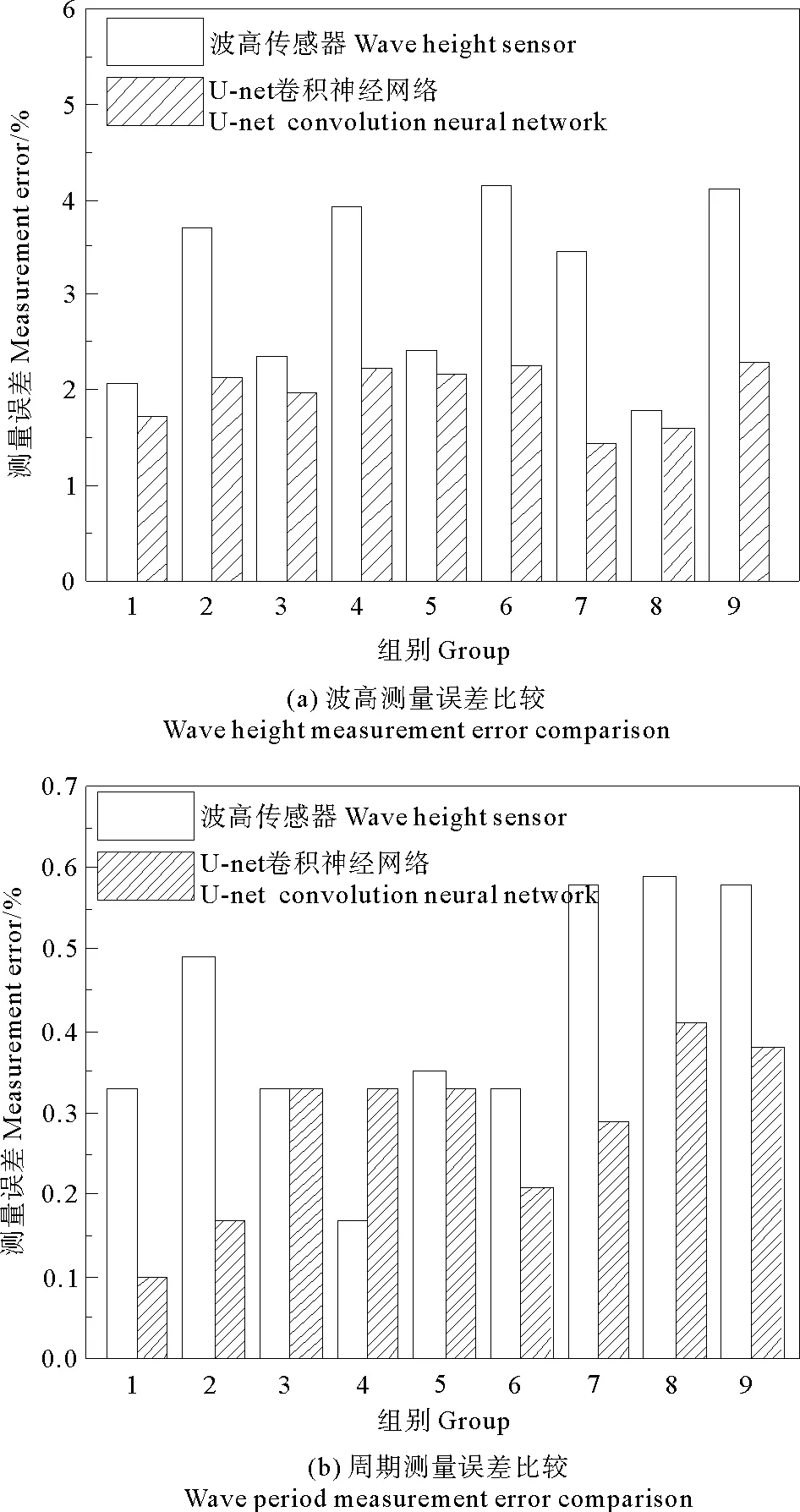
(图中白色矩形为波高传感器的测量误差，阴影矩形为U-net的测量误差。The white rectangle in the figure is the measurement error of the wave height sensor, and the shaded rectangle is the measurement error of the U-net.)

U-net卷积神经网络对不同组次的测量误差变化如图9所示。在周期相同、波高不同的工况下，规则波的测量误差都随着波高的增大而增大，且波高越大，测量误差越大。不规则波的测量误差也随波高增加而增加，且增加幅度更大，但都低于2.5%。此外，如图8(b)所示，U-net卷积神经网络测得的平均周期相对误差都在1%以内。上述结果说明了U-net卷积神经网络测量方法的准确性良好。

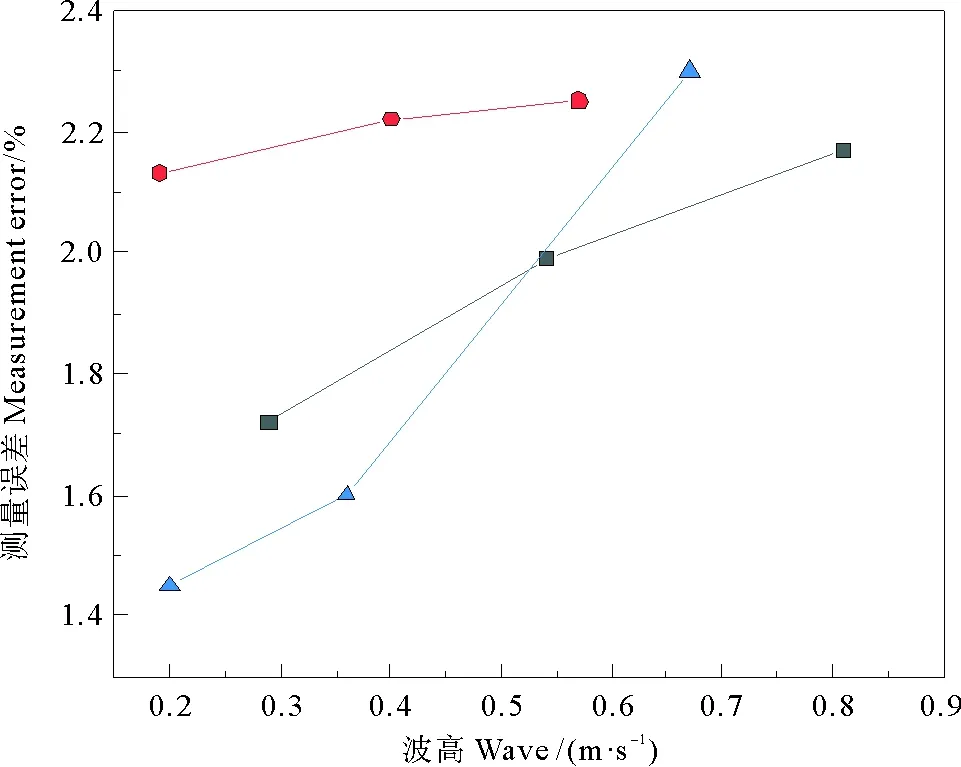
(红线是周期为6 s时的规则波，黑线是周期为3 s时的规则波，蓝线是周期为3.4 s时的不规则波。The red line is a regular wave with a period of 6 s, the black line is a regular wave with a period of 3 s, and the blue line is an irregular wave with a period of 3.4 s.)

3 适用性分析

(1)卷积神经网络需要学习大量数据才能实现良好的图像分割效果，网络模型的高泛化能力离不开种类繁多，数量丰富的数据集，前期数据集的搜集和模型的训练对本研究方法提出了一定的挑战。

(2)本文提出的U-net卷积神经网络波浪测量方法建立在视频图像的基础上，需要依靠波面图像中的标尺计算水位实际高度，因此，使用范围局限于能够完成图像坐标转换的场景中。

(3)基于U-net卷积神经网络的图像分割实质为端至端的像素级预测分割，需对每个像素点都进行类别判定输出，因此计算量较大，目前速度上还未实现实时测量，未来可进一步探索现场实时测量。

4 结语

本文提出了一种基于U-net卷积神经网络的波浪测量方法，在保持非接触式测量优点的基础上克服了光照波面对阈值图像分割测量影响较大的不足。实验结果表明，U-net卷积神经网络测量的相对误差最大为2.25%，而传感器误差最大为4.15%，因此，U-net卷积神经网络的波浪测量方法比波高传感器具有更高的波高测量精度，测量误差随波高的增大而增大，但平均波高相对误差均在2.5%以内，测得的平均周期误差都低于1%。上述结果证明了本研究方法的测量精度良好，为实验室的波浪测量提供了一种新的方法。