基于轴转矩补偿的永磁伺服系统机械谐振抑制

包广清, 杜赫轩, 祁武刚

(1. 兰州理工大学 电气工程与信息工程学院, 甘肃 兰州 730050; 2. 兰州理工大学 甘肃省工业先进控制重点实验室, 甘肃 兰州 730050; 3. 兰州理工大学 电气与控制工程国家级试验教学示范中心, 甘肃 兰州 730050)

交流永磁伺服系统以其优异的动态特性、跟踪特性以及控制精度,在工业机器人、航空航天、数控机床等电力传动领域中得到了广泛的应用.在伺服系统中,电机和负载之间常使用联轴器、传动轴、皮带轮以及滚珠丝杠等作为传动装置,由于其刚度有限,当伺服系统带宽覆盖柔性传动装置的固有谐振频率时,就会引发机械谐振[1-3],导致电机转速波动,影响电机转矩的稳定性,甚至会造成传动装置和电机轴的断裂从而引发安全事故.因此,如何有效抑制伺服系统机械谐振具有重要的现实意义.

目前抑制机械谐振的方式主要有主动控制方式和被动控制方式两种.被动控制方式是在速度环输出和电流环给定之间串入陷波滤波器,滤掉系统中的谐振频段[4-7].杨明[5]通过快速傅里叶变换(FFT)法实时分析交轴电流频率,在线辨识机械谐振频率,并以此自动整定陷波滤波器参数,实现了机械谐振的在线抑制.但是FFT法检测谐振频率速度较慢,而且需要一定的存储空间存放数据,不能很好地满足系统的实时性要求.

相对而言,主动控制方法具有更好的抑制效果.主动控制方式是通过改变控制器的结构和参数来抑制机械谐振.主要有：

1) 基于极点配置法设计控制器参数[8-9],通过改变系统的闭环传递函数得到合适的阻尼系数从而实现更好的机械谐振抑制效果.如王璨[8]采用极点配置法优化PI参数,调节系统极点位置,减小系统振荡.然而PI控制器只有2个可调参数,无法实现系统闭环传递函数零极点的自由配置.

2) 基于状态反馈的方法[10-14],通过角位移、角速度、角加速度和轴转矩等状态量对电磁转矩进行反馈补偿来抑制谐振.这类方法通过引入状态量的反馈,提高了系统极点配置的自由度.咸明辉[11]采用Luenberger观测器获取扰动转矩的观测值,经过一个比例积分环节负反馈到电流给定,并对反馈系数进行了整定,但观测器的设计并未考虑系统中的过程噪声与测量噪声.金杰[12]对比研究了电机侧、负载侧角加速度以及柔性轴两侧角加速度之差反馈对柔性系统谐振的影响,并通过合理配置极点保证系统的动态性能.丁有爽[13]提出了一种状态反馈与负载转矩前馈结合的控制策略,通过将谐振模态及其微分进行状态反馈实现系统极点的自由配置,并设计转矩前馈控制器实现了电机转速与负载转矩之间的解耦,有效地消除了柔性负载以及负载扰动的影响.赵寿华[14]设计了一种基于模型的自适应观测器来估计系统的多个状态,并设计了速度环线性二次型调节器在线抑制谐振.

3) 基于智能控制算法抑制谐振，如模糊自适应控制[15]、模型预测控制[16]和滑模变结构控制[17]等.这类方法虽然抑制效果好,但是由于算法复杂,在实际应用中难以推广.

基于上述分析,本文提出一种基于轴转矩补偿的主动抑制方法.该方法结构简单,无附加调节参数,可以消除柔性环节对电机端转速的影响;采用卡尔曼滤波器对轴转矩进行状态估计,避免了噪声对观测效果的影响.最后,通过仿真对该方法的有效性进行了验证.

1 数学模型建立

1.1 永磁同步电机的数学模型

为简化分析,在建模时作如下假设：

① 忽略铁心饱和；

② 忽略磁滞损耗；

③ 忽略谐波电流引起的涡流损耗；

④ 电机中的电流为对称的三相正弦波电流.

根据以上假设,建立永磁同步电动机在d-q坐标系下的数学模型为

(1)

电磁转矩为

Tm=pn[ψriq+(Ld-Lq)idiq]

(2)

式中:ud、uq分别为定子侧d、q轴电压；id、iq分别为定子侧d、q轴电流；Ld、Lq分别为定子侧d、q轴电感；Rs为定子侧电枢电阻；ωe为电机转子电角速度；ψr为转子永磁体磁链；pn为转子极对数.

对采用id=0矢量控制策略的表贴式永磁同步电机,由于Ls=Ld=Lq(Ls为定子侧电感),模型可以进一步简化为

(3)

电磁转矩为

Tm=pnψriq

(4)

1.2 柔性传动装置建模

柔性传动装置是指通过其柔性部分变形而产生位移和传动力的机械装置.柔性传动装置通常可以近似等效为如图1所示的两质量系统模型[1].图中:Jm为电机转动惯量；Jl为负载转动惯量；Ks为柔性传动装置的刚度系数；Tm为电机电磁转矩；Tl为负载转矩；Ts为柔性传动装置的轴扭矩；ωm、ωl分别为电机与负载的旋转角速度；θm、θl分别为电机与负载的角位移；cm、cl、cs分别为电机端、负载端以及柔性传动装置的机械阻尼系数.

图1 两质量模型示意图Fig.1 Schematic diagram of two mass model

由于传动装置具有弹性,需要扭转一定的角度才能传递扭矩,因此系统运行时电机端与负载端存在角度偏差,且轴扭矩与该角度偏差以及轴的刚度系数有关.根据以上分析建立如下微分方程：

(5)

忽略机械阻尼系数,对式(5)进行Laplace变换,得

(6)

由式(6)可以得到简化的两质量模型系统框图如图2所示.

图2 两质量模型框图Fig.2 Two mass model block diagram

由图2可以得到电机转矩到电机端转速和负载端转速的传递函数：

(7)

(8)

基于式(6)选取状态量x=[ωmωlTs]T.系统的状态空间方程可以写为

(9)

1.3 永磁同步电机通过柔性传动装置驱动负载的数学模型

结合式(3，4，9),可以得到永磁同步电机通过柔性传动装置驱动负载的数学模型.选取状态量为x=[iqωmωlθmθl]T,系统的状态方程可以写为

(10)

2 柔性传动对调速系统的影响

交流永磁伺服系统常采用双闭环矢量控制策略,本文通过对比柔性传动和刚性传动下电流环和转速环的开环幅频特性,分析柔性传动对调速系统带来的影响.

由式(2，3，7)可以得到uq和iq之间的传递函数为

(11)

结合式(4)和式(7),可以得到iq和ωm之间的传递函数为

(12)

双闭环调速系统的控制框图如图3所示,其中ωref为转速指令,iq,ref为电流指令,转速、电流调节器均采用PI调节.

图3 系统控制框图

2.1 电流环特性分析

对于刚性传动,电流环的开环传递函数为

(13)

对于柔性传动,电流环的开环传递函数为

(14)

可以发现,柔性传动通过电机的转速振荡影响永磁同步电机的反电势,从而将振荡分量引入调速系统电流内环.对比式(13)和式(14),发现柔性传动在电流环传递函数中的反电势项中引入了二阶项,为

(15)

由式(15)可知,柔性传动在系统中引入了一对共轭零点和共轭极点,共轭零点为反谐振频率ωarf,共轭极点为谐振频率ωrf：

(16)

零极点的存在使得系统对于特定频率产生较强的响应,造成机械谐振现象.

电流内环的开环幅频特性如图4所示.由图4可以看出,柔性传动在谐振频段处引起幅值衰减和相位变化.电流环幅值响应在反谐振频率点出现较大的反向谐振峰值,在谐振频率点出现较小的谐振峰值.而且系统的谐振频率落在电流环带宽边界,因此柔性传动对调速系统电流内环影响较小.

图4 电流环开环幅频特性Fig.4 Open loop Bode diagram of current loop

2.2 转速环特性分析

在双闭环调速系统中,电流环带宽远大于速度环带宽.通常认为转速外环在调节时,电流内环已经调节完成.因此可以忽略电流环的影响.此时调速系统可等效为图5.

图5 转速环控制框图Fig.5 Control block diagram of speed loop

对于柔性传动,转速环的开环传递函数为

(17)

对于刚性传动,转速环的开环传递函数为

(18)

转速外环的开环幅频特性如图6所示，可以看出,系统的谐振频率在转速环的带宽范围内.从幅频特性可以看出,系统在谐振频率处会发生幅值较大的谐振,因此转速外环受到柔性传动的影响较大.

图6 转速环开环幅频特性

3 轴转矩补偿的谐振抑制方法

3.1 轴转矩补偿原理

(19)

式中：Kt=pnψr.忽略轴转矩状态量估计值与实际值之间的误差,转速环的开环传递函数可近似写为

(20)

图7 基于轴转矩补偿的永磁伺服系统控制框图Fig.7 Control block diagram of permanent magnet servo system based on shaft torque compensation

由式(17)和式(20)对比,可以发现引入轴转矩补偿可以消除转速环中的二阶振荡环节,即消除了柔性传动对电机转速的影响,在电机转速响应中体现出了刚体传动特性,提高了电机转速的动态性能和抗干扰性能.由式(18)与式(20)对比,发现相较于刚性传动环节,引入轴转矩补偿后分母项的等效转动惯量由Jm+Jl变为Jm,因此引入轴转矩补偿可以提升转速的动态特性.

3.2 基于卡尔曼滤波器的轴转矩估计

对伺服系统而言,在系统工作过程中,会受到各种非确定性因素的干扰,因此由传感器测得的信号中含有随机噪声,为了保证观测精度,需要使用卡尔曼滤波器对轴转矩进行估计.卡尔曼滤波是一种基于系统状态方程,通过观测系统输入输出,对系统状态进行最优估计的递推算法.其基本思想是：考虑模型噪声,以最小均方误差为最佳估计原则,利用上一时刻的估计值与当前时刻的测量值更新状态变量的估计值.系统离散化的状态方程和量测方程为

(21)

x(k)=[ωm(k)ωl(k)Ts(k)

u(k)=Tm(k),y(k)=ωm(k)

式中:F为系统状态转移矩阵;G为控制矩阵;H为量测矩阵;x(k)为k时刻状态估计值;y(k)为k时刻状态估计值;u(k)为系统控制输入量;w(k-1)为过程噪声;v(k)为量测噪声；w(k-1)和v(k)是相互独立且满足高斯分布的白噪声.

卡尔曼滤波主要包括预测和校正两个过程.预测是利用时间更新方程对当前状态进行先验估计,得到当前时刻状态量和误差协方差的估计值;校正是利用量测值对当前先验估计值校正的后验估计.卡尔曼滤波的基本步骤如下：

1) 状态进一步预测：

(22)

2) 状态估算计算：

(23)

3) 滤波增益矩阵：

K(k)=P(k)-HT(k)[H(k)P(k)-HT(k)+R]-1

(24)

4) 更新协方差矩阵：

P(k)-=F(k)P(k)FT(k)+Q

(25)

5) 进一步预测协方差矩阵：

P(k)=[I-K(k)H(k)]P(k)-

(26)

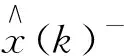
6) 卡尔曼滤波器初始化：

(27)

(28)

4 仿真验证

为了验证轴转矩补偿方法对机械谐振抑制的有效性,搭建了含有柔性传动的永磁同步电机伺服系统仿真模型.仿真参数为：电机额定功率为0.75 kW；额定电流为4.2 A；额定转速为3 000 r/min；额定转矩为2.9 N·m2;极对数为4对极；永磁磁链为0.119 4 Wb；定子电阻为0.048 5 Ω；定子电感为3.95 mH；轴的刚度系数为626 N·m/rad；电机转动惯量为1.1×10-3kg·m2；负载转动惯量为1×10-3kg·m2；系统给定转速为100 rad/s.

电机转速和柔性传动轴的轴转矩抑制前的仿真波形如图8所示.图中虚线为卡尔曼观测器的状态估计值,实线为状态实际值.由图8可以看出,在稳态时,电机转速和柔性传动轴的轴转矩存在小幅发散震荡.

图8 电机转速和轴转矩抑制前的仿真波形

电机转速和柔性传动轴的轴转矩抑制后的仿真波形如图9所示.由图9可以看出,引入轴转矩补偿后,系统中的机械谐振得到了有效的衰减,由此可以验证轴转矩补偿对机械谐振抑制的有效性.

图9 电机转速和轴转矩抑制后的仿真波形Fig.9 Simulation waveforms of motor speed and shaft torque after suppression

通过对比图8和图9可以发现,引入轴转矩补偿后,电机转速的上升时间由0.5 s变为0.3 s,超调量由18%变为31%.即引入轴转矩补偿后,系统的动态响应能力得到了提升,超调量也随之增加.

图10和图11分别为在1s和1.5s发生负载突变时的轴转矩响应与电机转速响应.可以看出,引入轴转矩补偿后系统具有良好的抗扰动能力.

图10 负载突变下的轴转矩响应

图11 负载突变下的转速响应Fig.11 Speed response under sudden load change

当转速指令为2+sin(40π)的正弦信号时,电机的转速响应如图12所示.图中虚线为转速指令,实线为电机实际转速.系统稳态误差为3.3%,表明引入轴转矩补偿后系统对给定信号有较好的跟踪效果.

图12 对转速指令的跟踪效果Fig.12 Follow effect of speed command

5 结论

针对柔性传动在永磁伺服系统中引发的机械谐振问题,本文提出了一种基于轴转矩补偿的抑制方法,并得出如下结论：

1) 通过将永磁同步电机数学模型和柔性传动轴的两质量模型结合,建立了永磁同步电机通过柔性传动轴驱动负载的数学模型.

2) 根据建立的系统模型,得到调速系统电流环以及转速环的传递函数,通过分析其开环幅频特性,发现柔性传动对转速环影响较大.

3) 针对柔性传动对转速环的影响,采用卡尔曼滤波器对轴转矩状态量进行估计并补偿到电流环给定,消除柔性传动对转速环的影响.

仿真结果表明,该方法可以有效抑制永磁伺服系统中的机械谐振,同时提高了系统的动态响应和跟踪特性,使系统具有较好的控制性能.