基于Gamma过程的金属材料剩余强度退化模型

韦尧兵, 赵 成, 张 震, 刘俭辉

(兰州理工大学 机电工程学院, 甘肃 兰州 730050)

工程零件在服役期间都会因承受循环载荷而导致疲劳失效,而疲劳失效是结构零件的主要失效形式之一[1-3].在循环载荷作用下,随着载荷循环作用次数增加,零件内部的疲劳损伤会因不断累积,而导致零件的剩余强度、安全性以及可靠性降低.由于服役工况存在复杂性,所以零件承受的循环载荷往往并不是恒幅载荷,而是变幅载荷,甚至是随机的.因此,如何建立多级载荷作用下剩余强度预测模型成为工程领域研究的热点问题之一.

剩余强度模型有很多,不同零件材料剩余强度衰减形式也存在差异,相应的剩余强度模型也各不相同.Wan等[4]提出了考虑缺口和应力比影响的S-N-R-D-R剩余强度模型,通过玻璃纤维3238A/EW250F和碳纤维3238A/CF3052这2种机织层合板(DEN)的疲劳试验数据验证了模型的准确性.Gao等[5]基于干涉理论提出了新的材料剩余强度概率模型,并利用单向碳/环氧树脂复合材料的疲劳试验数据验证了所提模型的有效性.Wang等[6]通过对自然腐蚀的钢板进行表面测量和拉伸实验,研究了腐蚀对钢板机械性能的影响,并基于轮廓的数值方法实现对钢板剩余强度的预测.Chen等[7]研究了平纹碳纤维增强环氧复合材料在随机疲劳载荷作用下的剩余强度和破坏概率.高建雄等[8]基于剩余强度和剩余寿命取决于材料内部同一损伤状态的假设,推导出随机载荷作用下风电叶片复合材料剩余强度的概率模型,并通过风电叶片复合材料层合板的静强度实验数据与疲劳寿命实验数据验证了模型的准确性.林小燕等[9]基于非线性疲劳损伤累积理论建立剩余强度预测模型,并通过材料的S-N曲线求解模型中的未知参数,最后将模型预测结果与材料实验结果进行比较,验证模型的合理性.李莉等[10]讨论了Schaff模型能较好地描述35CrMo的剩余强度退化规律.

零件的强度退化具有随机性和不可逆性,Gamma过程是独立、单增的过程,具有描述零件强度退化的基本特征[11].杨周等[12]利用Gamma过程来描述零件结构的强度退化过程,并对零件进行动态可靠性建模,结果表明,所建立的模型能准确反映出零件可靠度随时间的变化规律.吕昊等[13]利用Gamma函数描述强度退化随机过程,并利用摄动法、四阶矩法和Edgeworth级数法解决随机参数服从任意分布的可靠性计算问题,最后以螺栓为例验证该方法的有效性.安宗文等[14]建立基于P-S-N曲线的强度退化模型,并利用材料P-S-N曲线对Gamma过程的特征参数进行估计,最后以20CrMnTi钢疲劳试验数据验证模型的准确性.Yan等[15]考虑海洋船舶机构所受应力的随机性和强度降低过程的随机性,建立基于半随机过程的可靠性模型,最后利用Gamma过程求解未知参数.Zeng等[16]结合腐蚀速率的诺索克预测模型,考虑密封性能下降过程的随机性和不可逆性,提出基于Gamma过程的海底连接器密封性能下降的随机模型.

本文基于Schaff模型,考虑载荷加载次序对剩余强度的影响,引入载荷次序影响因子α,提出等损伤比剩余强度预估模型,推导出多级载荷作用下剩余强度表达式,在此基础上讨论了两级加载下剩余强度退化方式.剩余强度模型本身隐含着循环载荷作用下零部件的强度退化信息,考虑到强度退化具有随机性和不可逆性,Gamma过程具有单调递增的性质，因此,本文选用Gamma过程来描述零件的强度退化过程.假定Gamma过程的形状参数v为线性函数,利用45#钢和30CrMnSiA的疲劳试验数据验证模型的准确性,并估计Gamma过程的形状参数v和尺寸参数u.

1 剩余强度预测模型

剩余强度是指结构零件在经历载荷一定循环次数作用之后还具有的强度极限值,它从宏观上反映零件内部损伤状态的平均效应,是载荷的循环次数N与加载应力S的函数[17],因此剩余强度R(N)的表达式为

R(N)=f(N,S)

(1)

不同材料在循环载荷作用下剩余强度的退化规律是不同的,即使是同种材料在不同循环载荷作用下剩余强度的退化规律也存在差异.就金属材料而言,从疲劳机理上看,疲劳加载初期,零件在循环载荷作用下产生的缺陷,如位错、滑移、空洞等,对零件的强度影响很小；但后期零件内部会不断萌生出新裂纹,会引起有效接触面积减小,从而导致零件强度迅速降低,最终发生疲劳破坏.金属材料的剩余强度退化规律具有“突然死亡”的特点,即剩余强度开始降低得很慢,但当循环载荷比N/Nf接近1时剩余强度急剧降低,最终发生疲劳破坏.结合边界条件,剩余强度曲线应具有以下特征：

1)R0=σb,初始边界条件,剩余强度的初始值等于材料的静强度；

2)R(N)=Smax,破坏边界条件,剩余强度等于疲劳载荷峰值时,零件发生疲劳破坏,此时的循环数即为疲劳寿命Nf；

4)N→Nf时,具有“突然死亡”特点；

5)R(N)是单调递减函数.

满足特征1)和特征2)的一般函数为

R(N)=R0-(R0-Smax)f(N/Nf)

(2)

其中,

(3)

式中：R0为零件的初始静强度；Smax为循环载荷峰值；N为循环载荷作用次数；Nf为在载荷Smax作用下的疲劳寿命.

满足以上所有特征的模型有很多,本文选择Schaff剩余强度模型.该模型的优点在于需要确定的参数相对较少,精度也相对较高,在机械、电子、复合材料等领域得到了广泛的应用[18].模型定义为

(4)

其中，c为材料系数,c取不同值时,零件剩余强度的具体衰减形式也存在差异,当c=1时,剩余强度呈线性衰减,如图1所示.

图1 剩余强度退化规律Fig.1 Degradation law of residual strength

在实际工程中,一些关键的结构零件在服役期间往往承受多级载荷作用,甚至承受随机载荷的作用.因此,载荷加载次序和不同载荷的相互作用必然会对零件的剩余强度退化规律产生重要影响.本文引入载荷次序影响因子α(恒幅载荷时α=1),建立等损伤比剩余强度预估模型.模型定义为

(5)

其中,载荷次序影响因子α的定义式为

(6)

假设零件在循环载荷S1作用下的疲劳寿命为Nf1,则第1级载荷S1作用N1次后,零件的剩余强度为

(7)

零件在第2级载荷S2作用下的疲劳寿命为Nf2,基于文献[19],假设第2级载荷S2作用N′2次造成的损伤比等于第1级载荷S1作用N1次所造成的损伤比,即

(8)

其中,

(9)

原理如图2所示.

图2 等损伤比模型示意图

由式(7～9)可得:

(10)

其中,等效循环作用次数为

(11)

在循环载荷作用N1和N2次后,零件的剩余强度为

R(N1+N2)=R(N′2+N2)=

(12)

同理,可以推导出零件受到多级载荷Sk作用后的剩余强度表达式为

(13)

其中,

(14)

2 Gamma强度退化过程

零件的损伤会随着载荷作用次数的增加不断累积,强度会随之降低.从宏观表象上看,强度退化具有随机性和不可逆性两大特征[20].Gamma过程是有独立、非负增量并服从同一尺寸参数Gamma分布的随机过程,适合描述一系列随时间变化而产生微小增量的损伤过程,如零件的强度退化、腐蚀以及裂纹扩展等[21].

根据文献[22],设零件的强度退化量x(t)服从形状参数v和尺度参数u的Gamma分布,则Gamma分布的概率密度函数为

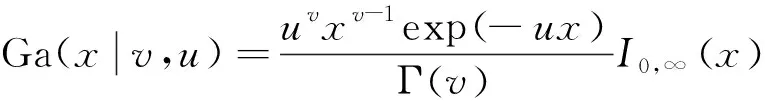
(15)

Gamma过程满足以下性质：

1)x(0)=0 ；

2) 对∀τ>t≥0,x(τ)-x(t)～Ga[x|v(τ)-v(t),u]；

3)x(t) 具有独立增量.

由Gamma过程的定义可得x(t)的均值和方差分别为

当形状参数v(t)为线性函数时,Gamma过程为平稳随机过程；当形状参数v(t)为非线性函数时,Gamma过程为非平稳随机过程.在疲劳试验中,零件的强度退化量随载荷次数的增加呈现平稳递增的趋势,不会出现大的波动和跳跃[14].因此,本文选择线性形状参数v(t)=at的Gamma过程来描述强度退化规律.零件使用过程中所受的载荷具有随机性,但最大载荷的期望和分布函数是不变的,即最大载荷的期望值和分布函数不会随时间发生改变.根据疲劳试验机的工作原理,循环次数比例是载荷在一段时间连续作用形成的,因此,可以将循环次数比例转换成关于时间t的函数,即

(18)

若零件在任意时间区间 (ti,tj) 内的强度退化量为ΔRij=R(ti)-R(tj)(i,j=1,2,…,n),则整个寿命周期内零件强度退化量的均值和方差估计值分别为

在循环载荷作用下,若零件的强度退化服从Gamma过程,则根据Gamma过程的性质,任意时间区间(ti,tj) 内的强度退化量ΔRij服从Ga[v(ti)-v(tj),u]分布,即零件强度退化量服从形状参数为v(ti)-v(tj)、尺寸参数为u的Gamma退化过程.

平稳Gamma过程的形状参数v(t)为线性函数,即v(t)=at≥0,则零件的强度退化量 ΔRij的均值和方差可表示为

(21)

(22)

由式(21)和式(22)可得：

(23)

将式(19)和式(20)代入式(23)可得：

(24)

对ui取均值,则得到平稳Gamma过程尺寸参数u的估计值为

(25)

将式(21)和式(22)相加可得：

(26)

则

(27)

将式(19)和式(20)代入式(27)可得：

(28)

对ai取平均值,从而得到Gamma过程特征参数a的估计值为

(29)

3 算例分析

3.1 剩余强度模型验证

3.1.1恒幅加载

45#钢经过调质处理后具有良好的综合机械性能,广泛应用于各种重要的结构零件,特别是处于交变载荷下工作的连杆、螺栓、齿轮及轴类等.45#钢在恒幅载荷作用下的疲劳试验数据和误差分析如表1所列[23].

通过MATLAB最小二乘法拟合得到45#钢剩余强度退化曲线如图3所示,式(5)常数c的拟合值为6.276.

由表1可以看出,剩余强度R(N)的预测值与实验值相对误差较小,最大误差仅为7.5%,表明本文模型预测精度较高.

图3 45#钢在恒幅载荷作用下的剩余强度Fig.3 Residual strength of 45#steel under constant loading

3.1.2两级加载

在验证两级载荷作用时,引用文献[24]中2组低-高、高-低加载得到的疲劳试验数据与本文模型预测结果进行对比,如表2所列.其中，加载的平均应力为250 MPa，低载荷应力为732 MPa,高载荷应力为836 MPa.

图4为30CrMnSiA在低-高、高-低不同加载次序下试验数据与本文模型预测结果的对比情况.可以看出,零件所受载荷的加载次序不同,剩余强度衰减的规律也不同.低-高加载时,循环次数比之和大于1；高-低加载时,循环次数比之和小于1.低-高加载时,Schaff模型的最大误差为17.26%,本文模型的最大误差仅为6.24%；高-低加载时,Schaff模型的最大误差为21.31%,本文模型的最大误差仅为9.27%.最大误差对比如表3所列.

图4 两级加载时30CrMnSiA剩余强度对比结果Fig.4 Comparison results of residual strength of 30CrMnSiA under two-stage loading

无论是低-高加载还是高-低加载,本文模型相比于Schaff模型,试验数据的分散性更小,预测精度更高.

3.2 Gamma过程参数估计

基于表1,可以计算出各时间区间的强度退化量,结果如表4所列.

将表4中的ΔRij分别代入式(19)和式(20)可得：

(32.59-174.586)2+(179.77-174.586)2+

(657.79-174.586)2}=62 734.639 MPa2

因此，45#钢的强度退化规律可以描述为服从形状参数v(t)=0.873t、尺寸参数u=2.783×10-3的Gamma分布.

低-高加载下，零件在t1=0.233时，各时间区间强度退化量估算结果如表5所列.

将表5中的ΔRij分别代入式(19)和式(20)可得：

同理可以得到，低-高加载下，t1=0.269、0.448、0.628、0.807时对应的ui和ai，如表6所列.

高-低加载下，t1=0.208、0.417、0.694时对应的ui和ai如表7所列.

由式(24)和式(28)可得，低-高加载下,Gamma退化过程的特征参数估计值分别为

高-低加载下,Gamma退化过程的特征参数估计值分别为

因此，30CrMnSiA在低-高加载下的强度退化规律可以描述为服从形状参数v(t)=7.609t、尺寸参数u=1.465×10-2的Gamma分布；在高-低加载下的强度退化规律可以描述为服从形状参数v(t)=7.104t、尺寸参数u=9.374×10-3的Gamma分布.

4 结论

1) 提出了考虑载荷加载次序影响的等损伤比剩余强度预测模型,并推导出多级载荷作用下剩余强度表达式.

2) 利用30CrMnSiA的疲劳试验数据讨论了零件在两级加载下剩余强度退化规律.低-高加载下,Schaff模型的最大误差为17.62%,本文模型的最大误差为6.24%；高-低加载下,Schaff模型的最大误差为21.31%,本文模型的最大误差为9.27%.结果表明本文模型预估精度要高于Schaff模型.

3) 基于剩余强度模型的强度退化量,估计了Gamma过程的形状参数和尺寸参数.结果表明,不同加载方式下,强度退化量服从不同的Gamma分布.