基于改进密度峰值聚类的异常流量检测

任 艳，徐 春，张 蕾，汪晓洁, 2

(1. 新疆财经大学 信息管理学院，新疆 乌鲁木齐 830012；2. 新疆大学 信息科学与工程学院，新疆 乌鲁木齐 830046)

互联网技术的迅速发展改变了人们的办公、生活以及娱乐模式。在我国，移动通信、电脑设备的数量都达到了数十亿的规模，同时也给用户带来了网络信息安全的威胁，人们的隐私安全隐患问题逐渐暴露，因此，互联网健康发展的关键是解决具有挑战性的网络信息安全问题[1]。

现今，人们生活中的各个方面都离不开互联网，如互联网金融、智能家居、智能医疗设备、智能网联汽车等。这些应用网络中存在规模巨大的数据交互信息，如果这些信息不加以保护，将会受到各种各样的网络攻击，甚至会导致计算机系统破坏。异常流量检测是网络信息安全领域中的一项重要的主动安全检测技术，可以检测出网络中的异常流量，从而保护网络安全，因此，通过异常流量检测发现潜在的非法的恶意行为，是解决网络信息安全问题的关键所在[2]。

近年来，国内外专家学者研究了各种网络中异常流量检测技术。Sommer等[3]提出了一种基于机器学习的网络异常流量检测技术方案，认为异常流量的行为与其他应用程序有着根本的不同，为后续的异常流量检测研究提供了指导。Srinivasa Murthy等[4]设计了一种基于贝叶斯和遗传算法(Bayesian and genetic algorithm, BAGA)的混合智能入侵检测系统，其中的贝叶斯算法将数据集分为各种类别以识别正常或攻击数据包，遗传算法通过对现有数据集应用变异操作来生成新数据集，根据高检测精度识别不同类型的攻击。胡明霞[5]提出了一种基于反向传播(back propagation，BP)神经网络的入侵检测算法方案，结合遗传算法解决了训练样本规模大、不易收敛的问题，提高了检测效率和正确率。Agyemang等[6]提出了一种基于统计的带参数的异常流量检测方案，将不符合设定的概率分布范围的流量判断为异常流量。与之相反，Rawashdeh等[7]提出了一种基于统计的不带参数的异常流量值检测方案。上述2种方案存在的共同缺陷是无法高效解决高维数据问题。杨茂林[8]提出了一种基于近邻的离群异常流量检测方案，与基于统计的异常流量值检测方案不同的是，它无须得知数据分布和预先标记就可以解决高维数据问题，但是其时间复杂度较高，不易选取结构复杂的数据的合适距离函数。Xu等[9]提出了一种无监督的聚类方案，基于网络用户日志数据的特征使用k均值算法对网络用户进行聚类，但是该方案的异常流量检测准确率较低，算法较为复杂。李佳玮等[10]提出了一种基于高斯混合聚类的异常检测方案，利用多元高斯分布混合算法对流量数据进行处理。上述的大部分算法非常依赖标签的正确性，原因是标签可以决定建立的模型所得出的最终结果；然而，当前复杂的网络攻击不断更新换代，这时标记通常会失效从而导致簇的误划分，因此，需要实时更改数据的标签。聚类算法作为一种经典且重要的无监督学习算法，显然更适合作为解决方案。Yang等[11]、Du等[12]提出一种自适应确定聚类中心的密度峰值聚类算法，可以自动识别簇中心点。Wu等[13]、Kamali等[14]提出了基于对称邻域的密度峰值聚类方法，可以高效地发现聚类中心。

在各类异常流量检测技术中，密度峰值聚类作为新型聚类方法，其优点是不需要任何预定义的参数和任何迭代过程。为了解决网络异常流量检测技术准确率较低、簇的误划分等问题，本文中提出一种基于改进的密度峰值聚类算法(improved density peaks clustering algorithm, IDPCA)的网络异常流量检测方案。该方案首先对网络流量数据进行预处理分组乱序，然后计算相应属性值并利用局部密度发现簇中心点，最后采用一种新的标签传递方式形成相应的簇群直至处理完所有数据。

1 聚类算法

作为一种无监督学习的经典方法，聚类算法在当前复杂的现实网络环境中极其重要。由于网络环境无法高度精准并高效获得规模较大的新收集流量的类别标记，因此聚类算法更适合作为当前异常流量检测的技术。

1.1 具有噪声的基于密度的聚类算法

与其他聚类算法相比，具有噪声的基于密度的聚类(density-based spatial clustering of applications with noise，DBSCAN)算法从数据对象的密钥出发，根据其密度相关性进行聚类，可在有噪声的空间数据中找出任意的簇，进一步研究不同数据对象之间的可连接性并不断扩充，最后得到聚类的结果。DBSCAN算法作为经典的算法，与划分聚类和层次聚类算法不同，可以找出密度较高的点，然后将该点周围高密度区域定义成簇。DBSCAN算法的相关定义如下：

1)邻域。以数据点为圆心、e为半径的圆定义为邻域，也就是该点与其他点的欧氏距离小于e的数据对象的集合，则该数据点的密度值为圈内数据点的个数。

2)核心点。给定邻域样本局部密度阈值Pmin，邻域内数据点的个数大于Pmin的圆心称为高密度的点或核心点，否则称为低密度的点。

3)密度直达。如果外围数据点m在核心数据点n的邻域内，则称外围数据点m由核心数据点n密度直达，即将高密度点的邻域内的高密度点连接起来，以此类推，然后将所有这样的点都连接起来。若低密度的点在高密度点的邻域内，把它与最近的高密度点相连接，则称为边界点。

4)密度可达。在外围数据点m与核心数据点n中，若存在相同的若干子数据点k，则称子数据点k由核心数据点n密度可达。

5)密度相连。在外围数据点m与核心数据点n中，如果存在外围数据点m由子数据点k密度可达且核心数据点n也由子数据点k密度可达，则称外围数据点m与核心数据点n密度相连。

图1所示为DBSCAN算法的相关定义示意图。其中，虚线表示预设数据点N1、N2、N3、N4、N5的邻域，图中所设置的Pmin为3，表示在邻域内有3个额外的数据点，可以看出，每个圈内都有4个数据点。数据点N2由数据点N1密度直达，数据点N3由数据点N1密度可达，数据点N6与数据点N1密度相连。

N1、N2、N3、N4、N5、N6—预设数据点。图1 具有噪声的基于密度的聚类算法的相关定义示意图

DBSCAN算法具体步骤如下：

步骤1初始化。设定样本数据集合D、邻域半径e、邻域样本局部密度阈值Pmin。

步骤2将样本数据集合D中所有数据点标记为未处理状态。

步骤3随机选择样本数据集合D中处于未处理状态的数据点m且为核心点，将其标记为已处理状态，若在数据点m的邻域内，至少包含Pmin个数据点，则建立一个新的簇C，并将邻域内所有数据点放入簇C。若数据点m是边缘点，则寻找下一个数据点。

步骤4重复步骤3，直至所有数据点都被处理。

步骤5输出聚类结果C。

1.2 密度峰值聚类算法

聚类算法的主要原理是将欧氏距离较小的点分为一个类簇，而欧氏距离较大的点分为其他的类簇。尽管聚类算法有很多种，但在聚类中的簇的定义依然没有统一的标准。

密度峰值聚类算法(density peaks clustering algorithm, DPCA)是一种新型的基于密度的聚类算法。该算法首先要确定簇的中心点，然后把其余的数据点加入到对应的类簇中。DPCA选取簇中心点有2个条件：第1个条件是选取的簇中心点在局部中是邻域内的密度峰值点，即最大密度值；第2个条件是这个簇中心点与其他类似局部较大密度的数据点的欧氏距离都较大。DPCA首先计算所有样本数据点的相对距离δ和局部密度ρ这2个属性值，然后基于这2个属性值构建相应的决策图，选取相对距离δ和局部密度ρ较大的数据点作为簇中心点，其他数据点依据局部密度ρ从大到小依次加入到相对距离δ最小的数据点所在的簇中。其中，任意数据点i的相对距离δi定义为

(1)

式中dij为任意数据点i与另一任意数据点j的欧氏距离。

若该数据点i具有整个全局最大密度，则它的距离定义为

(2)

即该数据点i的欧氏距离等于其他数据点与该点的最大距离。

任意数据点i的局部密度ρi定义为

其中

(3)

式中dc为截断距离。

式(3)的使用条件是在数据量较大时，局部密度的区分度较高。如果数据量较小，则需要采用高斯函数求出数据点i的局部密度ρi，即数据点i的邻域内数据点欧氏距离的加权值之和，以解决局部密度区分度低的问题。ρi的表达式为

(4)

DPCA流程如图2所示。

2 基于IDPCA的异常流量检测

IDPCA主要是针对网络异常流量检测中DPCA人工选择簇中心点容易造成簇的误划分问题提出的。该算法包括2个主要步骤：一是识别计算数据集中各个数据点的2个属性值；二是构建决策图并开始聚类。簇中心是在比相邻数据点密度更大的数据点中确定的，为此该算法采用2种不同的度量来识别簇中心点，然后采用标签传播距离算法对数据点进行聚类。IDPCA的步骤如下：

图2 密度峰值聚类算法流程

步骤1输入数据集合D、截断距离dc。

步骤2发现簇中心点。根据式(1)、(2)计算点距离矩阵，根据式(3)、(4)计算点的局部密度，构建决策图并选择簇中心点。

步骤3形成簇群。将簇中心点的标签分配给最近邻点，进行基于邻域距离矩阵和密度的聚类，将剩余的每个点分配到最近的聚类中心。

步骤4输出聚类结果簇C。

在步骤2中计算相应的数据，这与DPCA一致。不同的是，步骤2中提出了一种新的标签传递方式，最后根据处理过的簇中心点形成簇群，为每个簇中心点分配一个不同的标签，每个簇中心点将标签传递到其最近的邻点。对于没有任何标签或处理过的数据点i，如果其局部密度ρi小于ρj，则该数据点获得数据点j的标签。可以看出，IDPCA的时间复杂度为O(N2)，其中N是数据集D中样本数据点的个数。

基于IDPCA的异常流量检测流程如图3所示。

最后判断数据集中异常流量的规则，本文中定义异常流量样本满足以下条件：局部密度ρi小于Pmin，相对距离δi小于相对距离阈值δt，其中Pmin定义为

(5)

δt的定义为

(6)

式中γ1、γ2均为经验参数。

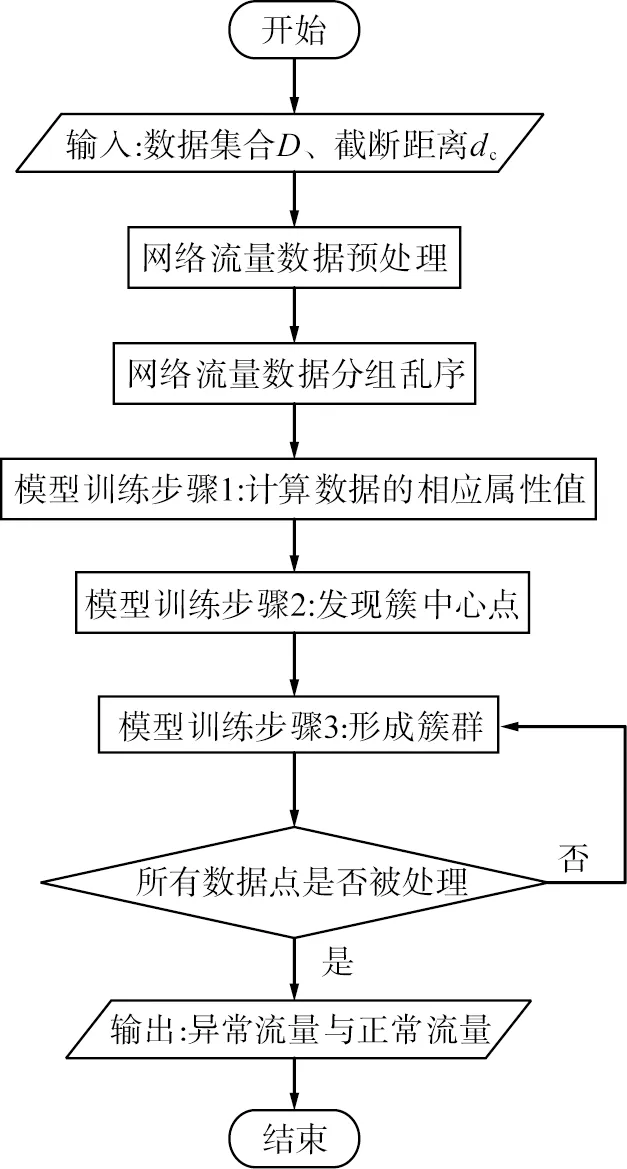
图3 基于改进的密度峰值聚类算法的异常流量检测流程

3 结果与分析

为了更好地检验IDPCA的有效性和网络异常流量检测性能，采用KDDCup99数据集进行仿真。仿真硬件环境为64位Windows 10操作系统的笔记本电脑，中央处理器(CPU) 为Intel 7，内存为8 GB；实验仿真的软件为Python 3、MATLAB R2018b。由于原始的KDDCup99数据集规模较大，因此学者们通常采用其中10%的数据作为研究对象，样本数据个数约为494 021。本文中采用的数据样本类型以及数据量如表1所示。

表1 KDDCup99数据集中部分实验数据集

对实验数据集进行预处理，首先对其中normal、smurf和neptune的数据进行降采样；然后将具有协议类型(protocol_type)离散特征的数据映射成整数型变量，再进行独热编码(one-hot code)操作；最后，将预处理过的实验数据进行乱序，取10组不同随机顺序的数据进行实验。

将IDPCA在给出的数据集上进行测试，以相对距离为y轴、局部密度为x轴构建相应的数据集决策图，如图4所示，相应的数据集聚类结果见图5。由实验结果可以看出，IDPCA算法基本可以识别所有的类簇。

图4 KDDCupp99数据集中部分数据集的决策图

图5 KDDCupp99数据集中部分数据集的聚类结果

将IDPCA与k均值算法、DBSCAN算法进行性能对比，分别从评测运行时间、完整性、同质性和检测准确率4个性能指标，性能指标描述与评测结果分别见表2、3。IDPCA、k均值算法均设置聚类中心数量为25，DBSCAN算法选择默认参数。

从表3中可以看出：在运行时间方面，k均值算法用时最短，仅为3.56 s，IDPCA仅次于它，而DBSCAN的运行时间较长；在完整性方面，分值越高越好，DBSCAN算法得分最高，IDPCA得分仍然居中，k均值算法得分最低；在同质性方面，IDPCA得分最高，k均值算法居中，DBSCAN算法得分最低；在检测准确率方面，IDPCA的准确率最高，k均值算法的次之，DBSCAN算法的最低。如果按照第1名的得3分、第2名得2分、第3名得1分计算，IDPCA的综合得分为10分，k均值算法的为8分，DBSCAN算法的为6分，因此，IDPCA在综合性能方面较有优势。

表2 聚类算法的性能指标及其描述

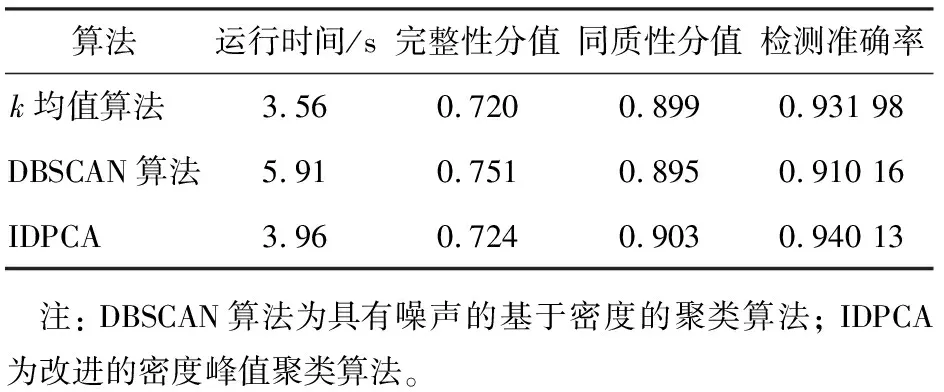
表3 不同聚类算法的性能指标评测结果

4 结论

在各种网络异常流量检测技术中，密度峰值聚类作为新型聚类方法，其优点是不需要任何预定义的参数和任何迭代过程。本文中提出基于IDPCA的网络异常流量检测方案，首先对网络流量数据进行预处理和分组乱序，然后计算相应属性值并利用局部密度发现簇中心点，最后采用一种新的标签传递方式形成相应的簇群直至处理完所有数据。实验结果表明，IDPCA提升了网络异常流量的检测准确率，综合性能优于k均值算法和DBSCAN算法。网络中的攻击流量往往是未知的，新型攻击流量不断出现，因此，在未来工作中将继续研究其他数据集的特征，并对相应的异常流量检测技术进行改进和完善。