三电平逆变器参数性故障诊断
2022-09-05陈正雄帕孜来马合木提
陈正雄,帕孜来·马合木提
(新疆大学 电气工程学院, 新疆 乌鲁木齐 830049)
随着光伏、风电的逐渐发展,并网系统对逆变器的成本、效率、可靠性等方面要求越来越高。三电平逆变器相对于传统两电平逆变器具有输出电压谐波含量低、功率损耗低、工作效率高等优点。目前,T型逆变器广泛应用于光伏并网、有源电力滤波器、电机驱动等领域[1-3]。据统计,绝缘栅双极型晶体管(insulated gate bipolar transistor,IGBT)在功率半导体器件故障中占比为42%[4],其中参数性故障是由环境、温度、过应力等因素导致IGBT焊料层疲劳失效、键合引线松动、电气失效等引起的,进而引起IGBT参数偏离标称值,如模块内阻、集射极电压增大。IGBT发生参数性故障后,逆变电路虽然能维持一定的功能;但是,随着器件参数的退化最终将导致器件功能的丧失[5-7],因此,针对逆变器IGBT参数性故障诊断进行研究,对提高逆变器系统的可靠性,为逆变器提供预知维护具有重要意义。
逆变器故障诊断分为基于模型和基于数据驱动2种方法。基于模型的方法以实时性强、精度高和能实现系统级的在线诊断等优点,成为研究的热点[8-9]。基于模型的方法是通过建立描述系统动态变化的数学模型和可测量信号产生残差,以残差为特征信号进行分析和处理的故障诊断技术[10]。目前,有学者采用混杂理论建立逆变器数学模型,但是存在状态方程过于复杂、求解困难、数学模型不唯一等一系列问题[11-13]。对于非线性复杂系统建模问题,很多学者针对基于键合图(bond graph,BG)的故障诊断方法开展深入研究。德国教授Borutzky长期致力于研究基于BG的故障诊断与隔离(fault diagnosis and isolation, FDI),提出了含有开关元件的混杂键合图(hybrid bond graph, HBG),为混杂系统FDI提供了基础[14]。文献[15]中采用多键合图理论对风力发电系统中的叶片、永磁同步发电机、三相整流器等建立行为模型,实现了风电系统多能域建模。文献[16]中采用双键合图理论对舰船主动装置建立数学模型,实现了系统参数FDI以及参数估计。
外界干扰和建模近似性是对过程状态进行在线分类决策的不确定性来源[17],因此需要设置合理的残差评估决策,减少系统故障的漏报、误报。针对系统参数不确定性问题,文献[18]中采用线性分式变换的键合图模型,将不确定的残差分离出来,提高了故障检测的精度。三电平逆变器结构复杂,采用线性分式变换的方法会加大建模的复杂性,同时该方法对不确定性部分进行了保守估计。文献[19]中利用Z检验分析残差获取观察特征,提高了推进系统故障检测的鲁棒性,但是只实现了部分参数故障隔离。
本文中针对三电平逆变器数学建模以及参数不确定性问题,提出一种基于解析冗余关系与模糊理论的参数性故障诊断方法;采用BG理论建立T型逆变器的数学模型,并且采用遗传算法(genetic algorithm, GA)优化隶属度函数进行残差评估,减少系统故障的漏报、误报。
1 系统分析与建模
1.1 BG理论
BG理论采用功率键、因果短划、基本元件表示元件之间的功率流向和因果关系。BG元件之间通过功率键进行能量交换,势e和流f的方向由短划线决定,功率的方向由半箭头决定,如图1所示。
元件集合{Se, Sf, R, I, C}为一通口元件,只有一个通口传输功率。势源Se和流源Sf分别为势和流的来源,阻性元件R为消耗功率元件,惯性元件I和容性元件C为储能元件。元件集合{GY, TF, 0, 1}为多通口元件,决定了系统的整体结构。回转器GY和变换器TF描述基本元件之间势与流的关系:0型节点上所有功率键的势相等,流的代数和为0;1型节点所有功率键的流相等,势的代数和为0。1型节点和0型节点分别相当于电路中的串联和并联[20]。
1.2 T型逆变器BG模型
T型逆变器的拓扑结构如图2所示。逆变器每一相有4个功率器件,其中功率器件Si2和Si3反向连接(i=a, b, c),实现中点电压钳位和续流的功能。由于逆变器三相对称,因此本文中以A相为例对IGBT参数性故障进行分析。T型逆变器每一相有3种工作模式,A相输出电压及开关状态如表1所示,开关管Sa1与Sa3互补导通,Sa2与Sa4互补导通。
关于功率开关管的建模问题,目前有众多方法来描述开关元件的连续、离散特性,但是都存在因果关系不确定等不足。文献[21]中将IGBT和反向并联的二极管用开关元件SW和关断电阻Roff等效,如图3所示。开关元件SW通过可调制变换器MTF连接脉冲信号a,且a(t)∈{0,1},∀t≥0。当a=1时SW导通,反之SW关断。
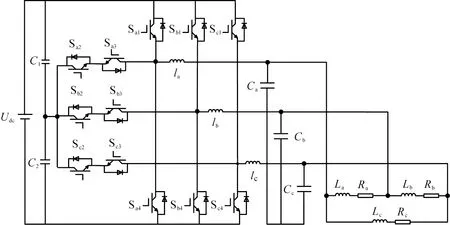
Udc—直流侧母线电压;C1、C2—直流侧电容;li、Ci、Li、Ri、Sij(i=a,b,c,j=1,2,3,4)—滤波电感、滤波电容、负载电感、负载电阻、功率开关管。图2 T型逆变器结构图
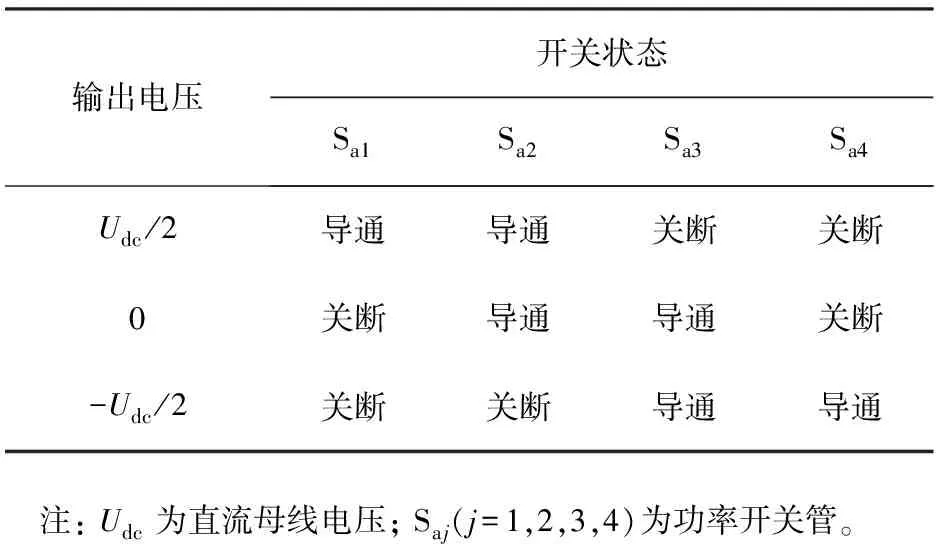
表1 A相输出电压及开关状态
结合BG理论和T型逆变器拓扑结构,建立如图4所示的BG模型,BG基本元件对应的电气元件标注其中。容性元件C∶C1、C∶C2和阻性元件R∶R1、R∶R2的添加是为了解决节点处因果关系冲突,设置为趋于0的值,在计算时可忽略不计。

SW—开关元件;Roff—关断电阻;a—脉冲信号;MTF—可调制变换器;Ron—导通电阻;P—键合图基本元件。图3 功率开关管等效原理图

1α(α=1,2,…,30)—串联型结点;0β(β=1,2,…,12)—并联型结点;Se—势源;C—容性元件;R—阻性元件;I—惯性元件;SW—开关元件;Roff j(j=1,2,3,4)—第j个开关元件关断电阻;Ron j(j=1,2,3,4)—第j个开关元件导通电阻;li、Ci、Li、Ri、(i=a,b,c)—滤波电感、滤波电容、负载电感、负载电阻;SWa j(j=1,2,3,4)—A相第j个开关元件。图4 T型逆变器键合图模型
1.3 解析冗余关系和故障特征矩阵

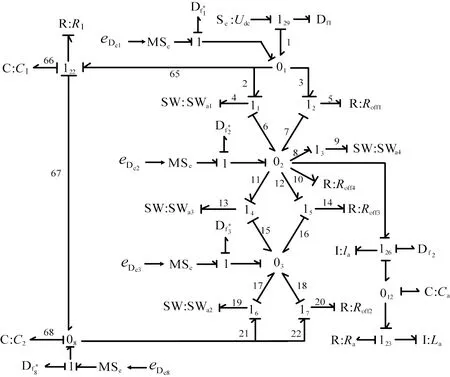
Df1、Df2—流传感器;eDek—势传感器Dek的测量值(k=1,2,3,8);MSe—检测势源;虚拟流传感器;1α(α=1,2,…,28)—串联型结点;0β(β=1,2,3,8)—并联型结点;Se—势源;C—容性元件;R—阻性元件;I—惯性元件;SW—开关元件;Roffj(j=1,2,3,4)—第j个开关元件关断电阻;Ron j(j=1,2,3,4)—第j个开关元件导通电阻;li、Ci、Li、Ri(i=a,b,c)—滤波电感、滤波电容、负载电感、负载电阻;SWa j(j=1,2,3,4)—A相第j个开关元件;数字1~68—功率键标号。图5 A相诊断键合图模型
根据因果路径法和各个元件之间的因果关系,消除未知变量推导出ARRs。含有系统开关模式信息的ARRs称之为全局解析冗余关系(global analytical redundancy relations, GARRs)。GARRs的数值即残差,当系统无故障时,残差为0;当系统发生故障时,残差不为0。根据结点01处流的代数和为0,可得
g1=f1-f2-f3-f23-f24-f44-f45-f65-r1=0 ,
(1)
式中:g1为结点处GARRs的表达式;fl(1≤l≤65)为第l个功率键上的流变量;r1为计算GARRs所得到的残差。
根据因果路径法以及元件的特性方程可知
f1=fDf1
,
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(9)
式(2)—(9)中:fDf1为流传感器Df1的测量值;aj(j=1,2,…,20)为开关SW的状态;eSe为势源Se的值;eDek(k=2,4,6,8)为势传感器Dek的测量值;C1为直流侧电容值。
根据式(1)—(9)得结点01处的残差r1,
(10)
同理,可得结点02、03、08处的残差r2、r3、r8分别为
(11)
(12)
(13)
式中:fDf2为流传感器Df2的测量值;C2为直流侧电容值。
故障特征矩阵(fault signature matrix, FSM)通过GARRs获得,反映了故障集合与残差集合之间的关系。FSM中的元素zpq为
(14)
式中:gp是第p个GARRs的表达式,p=1,2,…,m;m为GARRs的个数;θq是第q个故障参数,q=1,2,…,h,h为诊断元件的个数。
T型逆变器有3种运行模式(见表1),通过对逆变器各个模式下的FSM运用或功能合并,可得到如表2所示的A相FSM。表2中每一行的残差集合{r1,r2,r3,r8}组成了对应元件的故障特征矩阵。若某一个元件残差集合中至少有一个残差为1,则故障的可检测性参数Db=1;若残差集合唯一,则故障的可隔离性参数Ib=1。从表2中可知,A相所有元件均具有可检测性和可隔离性。
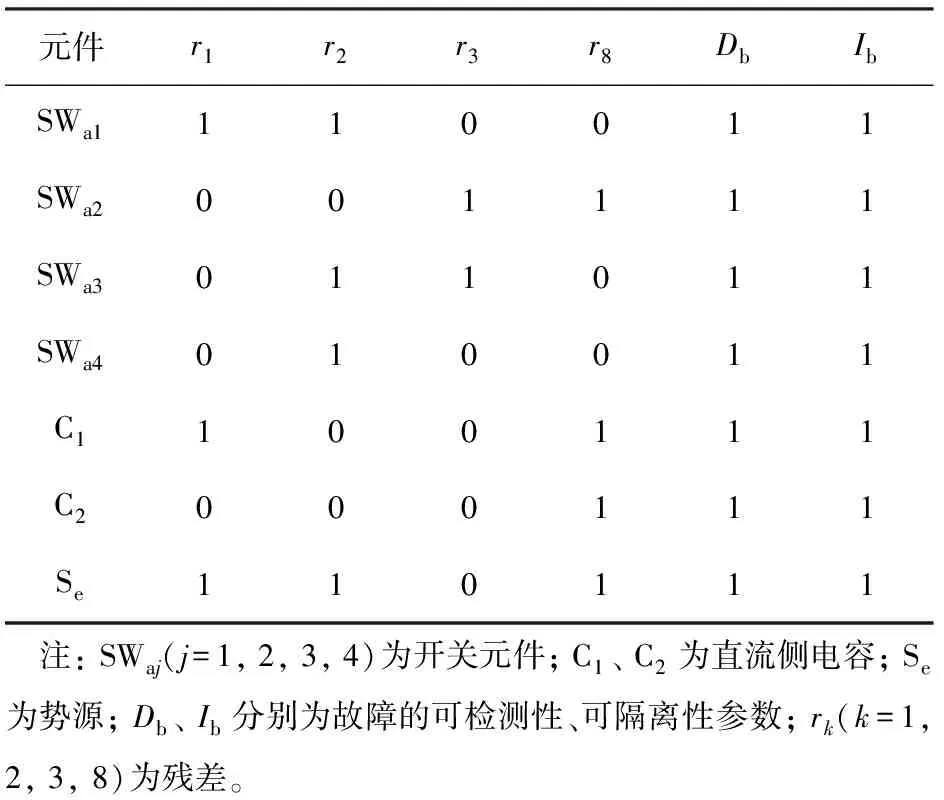
表2 A相故障特征矩阵
2 模糊检测
2.1 模糊检测系统设计
由于逆变器存在参数不确定性,而模糊理论是模拟不精确、模糊、不确定性的有力工具,因此为了提高故障检测的效果,本文中采用模糊理论进行残差评估,获取观察特征。模糊检测模块的输入由2组特征参数组成:
1)残差r的绝对值;
2)滑动时间窗口内残差变化量d,
(15)
式中:x为时刻,x=1,2,…,t; 参数N是固定的,参数N取较大的值,可提高检测的鲁棒性,同时会造成系统故障检测延迟。
模糊系统输入语言变量残差r的绝对值和残差变化量d的模糊子集为{小,大},其输入语言变量隶属度函数如图6所示。
反模糊化的输出为故障检测提供了故障索引,定义为故障指数H。故障指数模糊子集为{小,中,大},输出隶属度函数如图7所示。若故障指数接近0,表示系统正常;若故障指数接近1,则表示系统存在故障;若故障指数在区间[0.25,0.75]内,则检测存在问题。
模糊检测模块的模糊规则如表3所示,采用“极大-极小”合成规则。

|r|max—系统正常情况下残差r绝对值的最大值;|r′|min、|r′|max—系统故障情况下残差r绝对值的最小值和最大值;u—隶属度。(a)残差绝对值

dmax—系统正常情况下残差变化量d的最大值;Dmin、Dmax—系统故障情况下残差变化量d的最小值和最大值;u—隶属度。(b)残差变化量图6 输入语言量变量隶属度函数

H—故障指数; u—隶属度。图7 故障指数输出隶属度函数
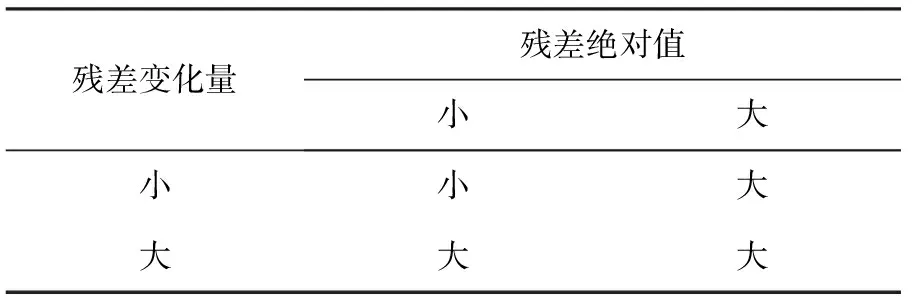
表3 模糊规则诊断表
2.2 GA优化模糊检测系统
确定隶属度函数的方法一般通过专家经验和实际应用中的调整;但是这种根据经验的设计无法取得较好的检测效果,因此本文中在模糊规则确定的情况下,采用GA优化输入隶属度函数参数如下: 系统正常情况下残差r绝对值的最大值|r|max、系统故障情况下残差r绝对值的最小值|r′|min、系统正常情况下残差变化量d的最大值dmax、系统故障情况下残差变化量d的最小值Dmin,系统故障情况下残差r绝对值、残差变化量d的最大值|r′|max、Dmax分别通过实验确定。GA优化模糊检测结构框图如图8所示。

|r(t)|—时间序列的残差绝对值;d(t)—时间序列的残差变化量; H(t)—时间序列的故障指数;GA—遗传算法。图8 遗传算法优化模糊检测结构框图
故障检测过程中可以把模糊检测模块理解为一个分类问题,即判断当前时刻系统是否发生故障。目标函数J定义为
(16)
式中:yg为期望的第g个故障指数,g=1,2,…,K,K为某时间段内故障指数的个数;bg为由模糊系统实际输出的第g个故障指数。
模糊检测模块的目标是做出正确的故障决策,因此目标函数的值越小越好,同时目标函数是非负的,故适应度函数F为
(17)
GA优化模糊检测的流程如图9所示。GA参数设置如下:最大迭代次数120,种群个数为130,隶属度函数参数采用二进制编码,染色体长度为40。

图9 遗传算法优化模糊检测流程
采用单点交叉,在个体串中随机选取一个交叉点,交叉点前或后的2个个体的部分结构发生改变,交叉概率pc=0.9。采用单点变异,变异概率随着迭代次数的增加而逐渐减小,最大变异概率pm=0.1。
3 仿真实验
3.1 键合图模型仿真验证
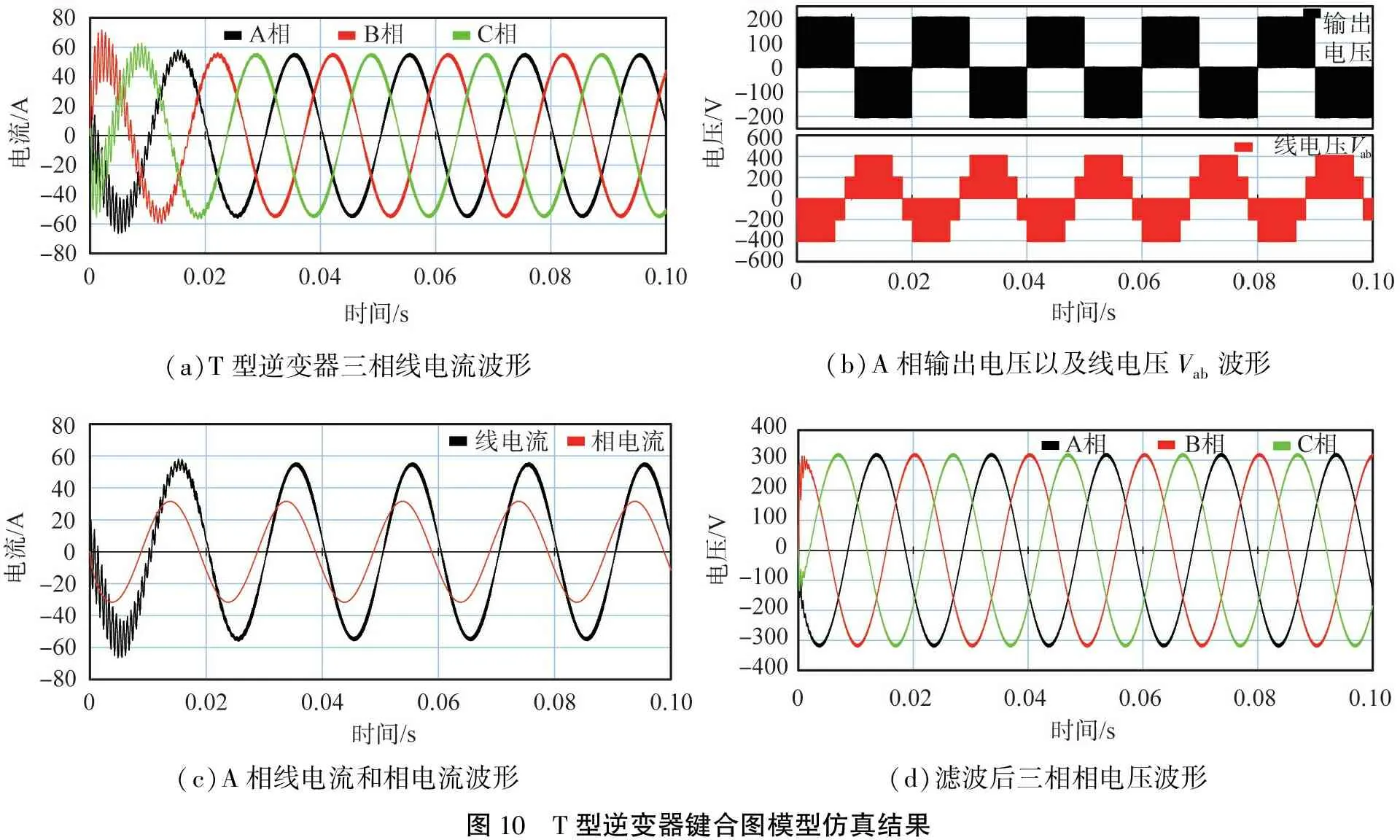
(a)T型逆变器三相线电流波形(b)A相输出电压以及线电压Vab波形(c)A相线电流和相电流波形 (d)滤波后三相相电压波形图10 T型逆变器键合图模型仿真结果
3.2 观测特征仿真验证
当系统无故障时,A相相关残差变化曲线如图11所示。从图可知,当系统正常运行时残差为接近于0的极小值,这是由系统参数不确定造成的。
当SWa1在0.4 s发生1%参数性故障时,即Sa1发生参数性故障,在0.4 s时电阻Ron1值增大1%,A相残差的变化如图12所示。由图可见,残差r1、r2在0.4 s后的数值发生明显变化,而残差r3、r8始终非常小。
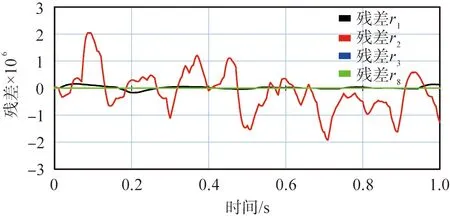
图11 系统无故障时的残差变化曲线
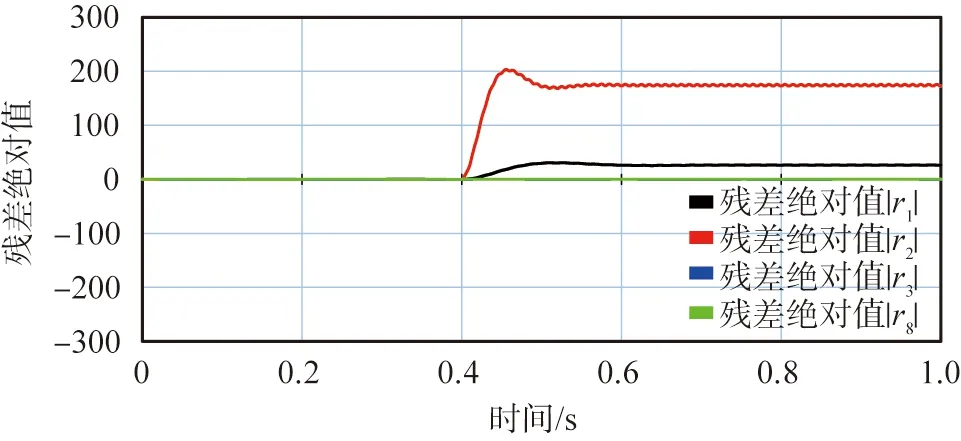
图12 开关管SWa1发生电阻值增大1%参数性故障时A相残差绝对值变化曲线
本文中设定IGBT参数的不确定度为1%,即在1%的参数不确定下系统为正常状态。同时在残差信号中加入白噪声来模拟外界干扰带来的不确定性。在0.4 s时开关管SWa1发生参数性故障时,采用模糊检测的方法进行残差评估,A相相关残差的故障指数如图13所示。由于残差绝对值|r1|和|r2|在发生故障后并不是突变,而是缓慢上升,因此在0.4 s后故障指数H1、H2并不是全为1,但接近于1。从图可知,SWa1发生故障后的观测特征向量为(1 1 0 0)与表2中SWa1的故障特征向量一致,因此可以定位到SWa1发生参数性故障。

图13 开关管SWa1发生参数性故障时A相相关残差的故障指数
故障指数H1、H2的目标函数J收敛图见图14。
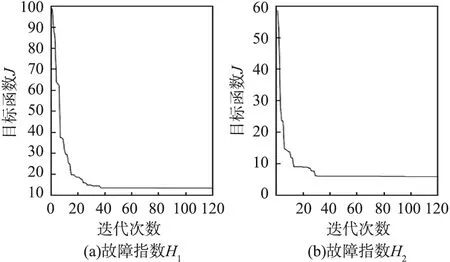
图14 不同故障指数的目标函数J变化过程
修正后的隶属度函数可以有效减少系统参数故障漏报、误报。开关管SWa2、SWa3、SWa4分别在0.4 s发生参数性故障时,A相相关残差的故障指数变化如图15所示。由图可知,当开关管分别在0.4 s后发生参数性故障,A相相关残差故障指数得出的观察特征向量与表2故障特征向量一致,因此均可定位到相应开关管故障。
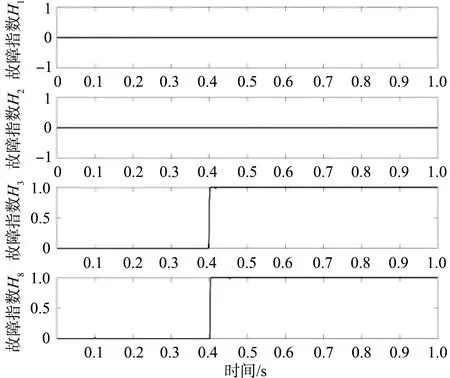
(a)开关管SWa2

(b)开关管SWa3
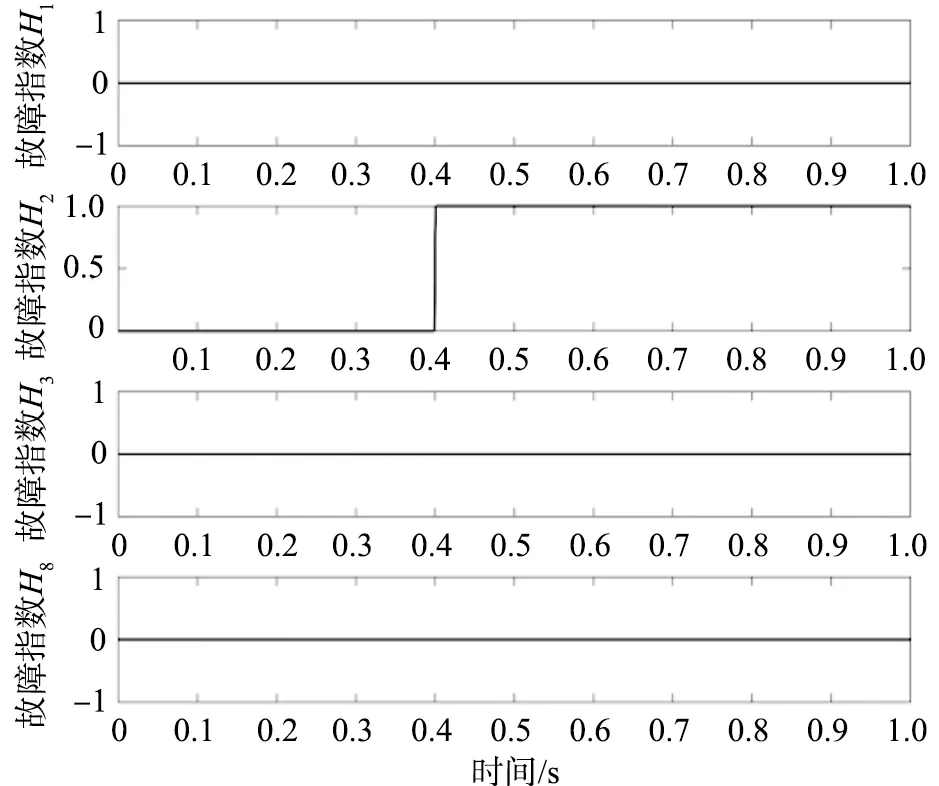
(c)开关管SWa4图15 开关管SWa2、SWa3、SWa4分别发生参数性故障时A相相关残差的故障指数
4 结论
本文中提出结合GARRs与模糊理论的三电平逆变器参数性故障诊断方法,即故障检测基于模糊理论对残差评估,故障隔离基于GARRs。T型逆变器参数性故障诊断结果表明:
1)基于BG理论的三电平逆变器建模方法,能够克服强非线性复杂系统难以诊断模型的问题。
2)根据诊断键合图模型推导系统的GARRs能够实现逆变器参数性故障隔离。
3)利用模糊理论处理参数不确定性问题,通过对T型逆变器A相IGBT参数性故障仿真验证表明,采用模糊逻辑进行残差评估可以减少故障漏报、误报,实现参数性故障的有效检测。
