位移放大型黏弹性减震系统力学模型与地震响应分析

2022-09-03刘文光吴铭智何文福

振动工程学报 2022年4期

刘文光，吴铭智，何文福，许浩

（上海大学土木工程系，上海 200444）

引言

随着地震的频发，耗能减震技术［1⁃3］受到国内外研究者的重视。目前国内外学者已经开发了多种不同类型和不同构造的耗能减震装置［4⁃6］。由于耗能减震技术研究和应用的历史较短，在一些工程应用中，如钢筋混凝土剪力墙结构、钢支撑体系及木框架结构，其在小震下的弹性位移不足，使耗能装置未能发挥作用，甚至无法启动［7］。

将位移放大装置应用于耗能装置中［8］，不仅能通过放大相对位移和相对速度来增加阻尼器的耗能，且能增大阻尼器在最大位移处的阻尼力。在一定程度上可解决上述问题。为此国内外学者开展了一系列的研究。陈月明等［9］提出一种带有梯形杠杆摆的黏弹性阻尼器，在框架中设置人字形支撑，依据杠杆原理将层间位移放大几倍，将该放大量传递给黏弹性阻尼材料进而减少了结构的地震与风振反应。Berton 等［10］采用齿条齿轮放大装置来放大结构传给阻尼墙的位移，通过试验研究证明了齿条齿轮放大装置的有效性。Watakabe 等［11］提出一种管形黏弹性阻尼器，研究表明带位移放大功能的管形阻尼器对结构振动响应的控制效果较好。刘文光等［12］提出了一种带位移放大杠杆的黏滞阻尼墙装置，并进行了理论和振动台试验研究，验证了该装置增效减震效果。韩建平等［13］为了解决结构层间位移较小使阻尼器无法发挥效果的问题，提出使用齿轮机构放大的流体黏滞阻尼器，分析表明安装此阻尼器的结构层间位移有不同程度的减小，效果优于普通黏滞阻尼器。

综上，位移放大系统能更有效地降低结构动力响应，达到充分耗能的效果。然而针对基于杠杆原理的位移放大黏弹性阻尼器的理论推导及数值模拟简化分析方法还有待进一步研究。本文提出一种位移放大型黏弹阻尼器，并进行了理论分析，设计制作了2.5 倍位移放大装置的黏弹性阻尼器和普通阻尼器试验模型，完成了力学性能试验。最后针对布置不同类型阻尼器的某框架减震结构，进行地震响应对比分析，重点研究位移放大型黏弹性减震系统的减震效果。

1 阻尼器构造与力学模型

1.1 装置构造

位移放大型黏弹性阻尼器主要由位移放大机构、支点轴、连接板、阻尼器外钢板和活动钢板等组成。如图1（a）所示。在层间位移较小情况下，放大其相对位移和相对速度，从而产生更大的阻尼力，提高耗能效果。

图1（b）为位移放大型黏弹性阻尼器工作原理图，在激励荷载作用下，结构的层间位移u通过位移放大机构放大后作用于阻尼器的活动钢板，使阻尼器的相对位移增大到ηu，提升其耗能能力。

图1 位移放大型黏弹性阻尼器示意图、工作原理图及简化模型图Fig.1 Schematic diagram，working principle diagram and simplified model diagram of displacement⁃amplified viscoelastic damper

1.2 位移放大型黏弹性阻尼器的理论分析

位移放大型黏弹性阻尼器采用高阻尼黏弹性材料，利用高阻尼黏弹性材料的阻尼器其滞回曲线呈双线性特征，可采用通用Bouc⁃Wen［14］计算模型模拟其滞回曲线。

Bouc⁃Wen 模型的计算公式如下：

式中k表示初始弹性刚度；d表示阻尼器两端相对位移；σy表示屈服力；r表示屈服后刚度对初始弹性刚度k的比值；z表示内部滞后变量，此变量范围为|z|≤1，其中|z|=1 代表屈服面。α，β，A和n分别为滞回曲线控制参数。

高阻尼黏弹性阻尼器的阻尼力及耗能公式可分别表示为：

式中F表示阻尼力；E表示消耗的能量；u表示结构层间位移。图1（c）为位移放大型黏弹性阻尼器的简化力学模型。图中M，K，C分别表示原结构楼层的质量、刚度和阻尼，L和ηL分别为位移放大机构上、下部分的长度，η为位移放大机构的放大倍率；ηu表示位移放大倍率为η倍的位移放大型黏弹性阻尼器的运动位移。

放大倍率为η的位移放大型黏弹性阻尼器，内钢板阻尼力计算公式为：

式中k'为位移放大型黏弹性阻尼器初始弹性刚度；r'为屈服后刚度对初始弹性刚度k'的比值；σ′y为屈服力。位移放大型黏弹性阻尼器初始弹性刚度k'、屈服力σ′y为一定值，不随加载位移及频率的变化而变化，即：

将式（6）～（8）代入式（5），得：

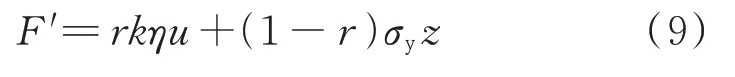
对于位移放大型黏弹性阻尼器，根据位移放大力学原理，其阻尼力表示为：

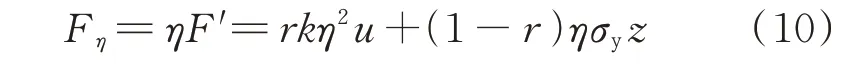
令：keq=η2k，r=req，σyeq=ησy，式（10）可表示为：

因此位移放大型黏弹性阻尼器阻尼力和耗能公式可分别表示为：

1.3 不同放大倍率下力学模型对比

为了分析不同放大倍率下位移放大型黏弹性阻尼器的情况，分别针对普通黏弹性阻尼器和放大倍率为2 倍、2.5 倍及3 倍的位移放大型黏弹性阻尼器进行受力分析。分析参数如下：u0=10 mm，f=0.1 Hz，k=88.23 kN/mm，r=0.0204，σy=14.28 kN，u=u0×sin(2πft)。分析结果如图2（a）所示，位移放大型黏弹性阻尼器表现出了显著的双线性滞回特征，且放大倍率越高滞回曲线越饱满。图2（b）为不同放大倍率下位移放大型黏弹性阻尼器的刚度、阻尼力及耗能对比，随着放大倍率η的增大，阻尼力、刚度及耗能的放大倍数也随之提高，并且在不同放大倍率下，阻尼力和刚度的放大倍数呈现一致性，以近似线性规律放大。当放大倍率为3 时，位移放大型黏弹性阻尼器单圈滞回面积为普通阻尼器的2.65 倍，体现出了良好的耗能能力。

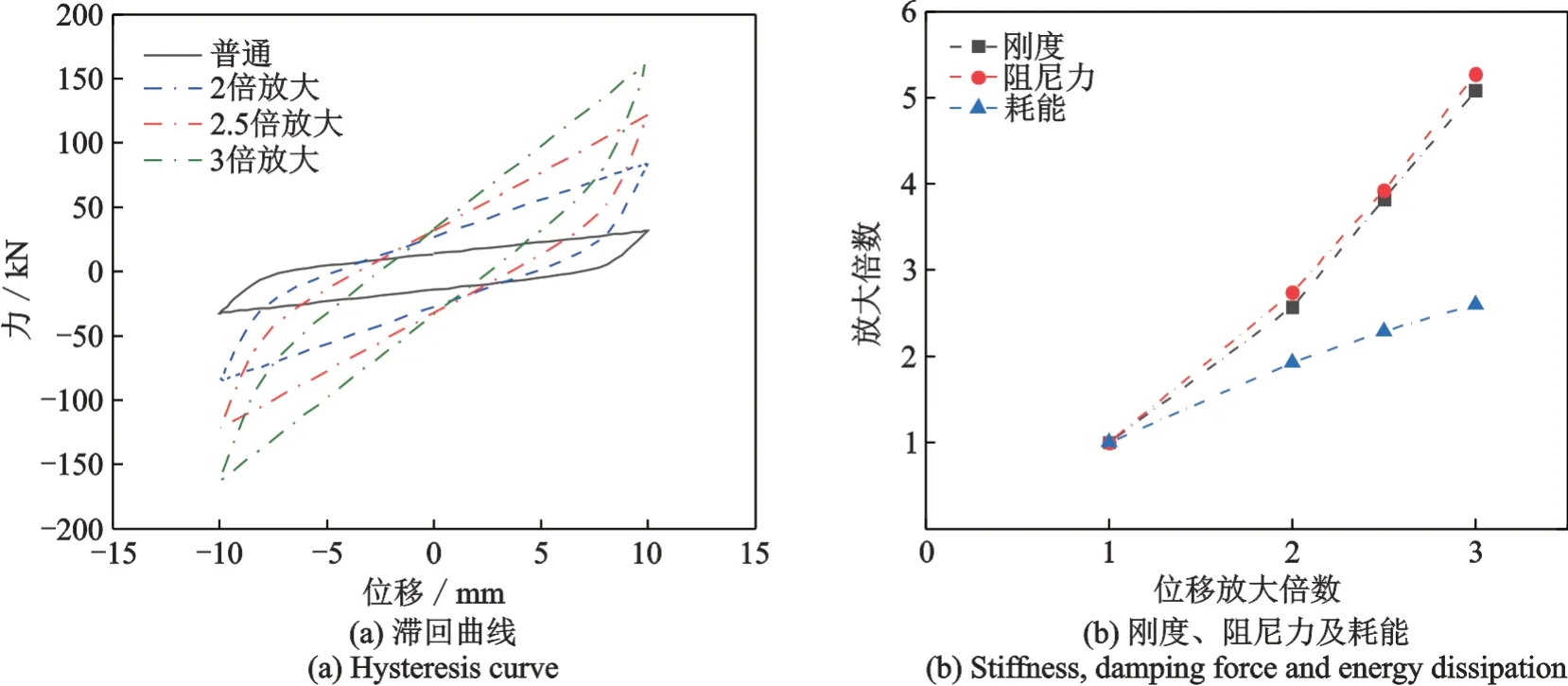
图2 阻尼器滞回曲线、刚度、阻尼力及耗能对比Fig.2 Comparison of damper hysteresis curve，stiffness，damping force and energy dissipation

2 模型装置力学性能试验

2.1 试验概况

本试验采用电液伺服压剪试验系统进行加载，作动器水平最大输出力为1000 kN，最大工程行程为±1200 mm。加载设备如图3所示。加载方式为位移控制的正弦波循环加载。阻尼器上连接板与作动器固定连接，通过伺服作动器自身的位移控制反馈值作为加载目标值，进行位移控制的正弦加载。

图3 加载装置图Fig.3 Loading device diagram

为配合试验设备，设计了位移放大型黏弹性阻尼器，阻尼器长为400 mm，宽为150 mm，高为605 mm。由Q345 钢板焊接而成，M12.9 级螺栓连接。位移放大型黏弹性阻尼器其他参数如表1所示。试件模型尺寸如图4所示。加工完成后的普通黏弹性阻尼器和位移放大型黏弹性阻尼器实物图如图5所示。其中，位移放大装置的构造为两根杠杆。每根杠杆上有三个螺栓孔，分别通过螺栓将杠杆固定于上连接板、外钢板的支点孔和活动钢板。

图4 模型尺寸示意图（单位：mm）Fig.4 Schematic of model size（Unit：mm）

图5 阻尼器实物图Fig.5 Pictures of dampers

表1 阻尼器参数Tab.1 Damper parameter

为了分析位移放大型黏弹阻尼器和普通阻尼器的力学性能特点。工况设计保证各种参量等间隔增加，试验加载位移分别为±5 mm，±7.5 mm，±10 mm，±15 mm，±20 mm，加载频率为0.1 Hz。其中，位移放大型阻尼器的放大倍率为2.5 倍，试验所用的高阻尼黏弹性材料弹性模量为0.5 MPa，尺寸为300 mm×200 mm，厚度为20 mm。

2.2 试验结果及分析

2.2.1 力学性能分析

表2给出了位移放大型黏弹性阻尼器和普通黏弹性阻尼器在不同工况下的阻尼力、刚度及耗能结果，在相同加载位移幅值下位移放大型阻尼器的刚度、阻尼力及耗能能力比普通阻尼器有显著提升。加载位移幅值为5，7.5，10，15，20 mm 时，位移放大型阻尼器与普通阻尼器的刚度之比分别为4.26，4.16，4.21，4.00，3.56，平均放大4.04 倍；阻尼力之比分别为4.22，4.15，4.20，3.99，3.55，平均放大4.02 倍；耗能之比分别为1.74，2.02，2.32，2.44，2.37，平均放大2.18 倍。且随着加载位移幅值的增加，2.5 倍位移放大型黏弹性阻尼器的阻尼力和耗能有显著的提升。

表2 分析结果Tab.2 Analysis results

图6给出了不同位移幅值加载工况下2.5 倍位移放大型黏弹性阻尼器和普通黏弹性阻尼器滞回曲线对比效果。当加载频率恒定时，随位移加载幅值的增加，2.5 倍位移放大型黏弹性阻尼器的阻尼力远大于普通黏弹性阻尼器，且滞回曲线更为饱满，耗能能力显著提升。位移放大型黏弹性阻尼器的滞回曲线表现出了显著的双线性滞回特性，在较大位移作用下，曲线更为饱满，具有良好的耗能效果，体现出黏弹性材料在剪切变形中发挥了良好的作用；在卸载与重复加载过程中，滞回曲线有明显的圆弧过渡段，体现出黏弹性材料的性能。

图6 两种阻尼器试验滞回曲线对比Fig.6 The comparison of hysteretic curves of the two dampers

2.2.2 试验结果与理论模型对比

根据前文提出的Bouc⁃Wen 模型，以及通过文献［15］中的相关推导，可得出Bouc⁃Wen 模型的相关公式，并编写了相应程序，程序中模型的控制参数为：α=0.5，β=0.5，n=1，A=1，模型中的其他参数如表3所示。

表3 Bouc‑wen 模型力学参数Tab.3 Mechanical parameters of Bouc‑Wen model

表4和5 分别给出普通黏弹性阻尼器和位移放大型黏弹性的试验值与理论分析的对比结果，其力学模型与试验结果吻合，误差均在10%以内。其中，位移放大型黏弹性阻尼器的刚度、阻尼力与耗能的误差分别为2.98%，4.70%，5.70%。普通阻尼器的刚度、阻尼力与耗能的误差分别为5.31%，3.30%，7.43%。

表4 普通阻尼器试验值和理论值对比Tab.4 Comparison of experimental and theoretical values of ordinary dampers

图7给出了刚度、阻尼力及耗能随加载位移幅值的变化规律。在不同位移幅值下，普通阻尼器和位移放大型阻尼器的试验值与理论值吻合。随位移加载幅值的增加阻尼器刚度减小，其阻尼力及耗能能力显著增加，且位移放大型阻尼器增加幅值远大于普通阻尼器。

《中国移动互联网发展报告(2017)》蓝皮书调查数据显示，我国移动互联网用户规模连续三年保持11%左右增长率。2016年一季度，移动端阅读人数较桌面电脑端多2 000万人。随着移动通信技术的研发与应用，主流移动手机终端己具备流畅接收与处理图片、音频、视频等多媒体资源的能力。人们可以不受时空限制获取信息，学习形式呈现碎片化特点，移动学习(M-Learning)兴起。移动学习是利用无线网络技术，通过智能手机、个人数字助理PDA等无线移动通信设备获取教育信息、教育资源和教育服务的一种新型数字化学习形式[2]。

图7 普通阻尼器与位移放大型阻尼器力学性能的试验和理论值对比Fig.7 Experimental and theoretical values of mechanical properties of ordinary dampers and displacement⁃amplified dampers

图8和9 给出了普通阻尼器和位移放大型阻尼器在不同工况下试验和理论滞回曲线的对比结果，最大阻尼力与滞回面积的试验值与理论值基本一致。其中，位移放大型阻尼器滞回曲线与理论值在小位移段和卸载段存在一定偏差，原因为在小位移段，黏弹性材料存在非线性变形及螺栓连接存在缝隙，但对整体耗能和刚度影响不大。

图8 普通阻尼器曲线拟合的对比Fig.8 Comparison of ordinary damper fitting curves

3 黏弹性减震结构地震响应分析

3.1 工程概况

选取某框架结构进行地震响应分析。该结构首层楼高4.5 m，其余各楼层高度均为3.6 m。第一层到第六层的框架柱截面的截面尺寸为600 mm×600 mm。七至十层框架柱的截面尺寸为500 mm×500 mm。梁截面尺寸为300 mm×700 mm。柱采用C40 混凝土，梁、板均采用C35 混凝土，受力主筋采用HRB335。结构总重5440.95 t。抗震设防烈度为8 度，设计地震分组为第二组，场地类别为Ⅱ类场地。

按照《抗震规范》要求，时程分析过程中采用一条人工波、两条天然波：RH2 波、TH2 波、TH57 波，地震动输入峰值为70 Gal。

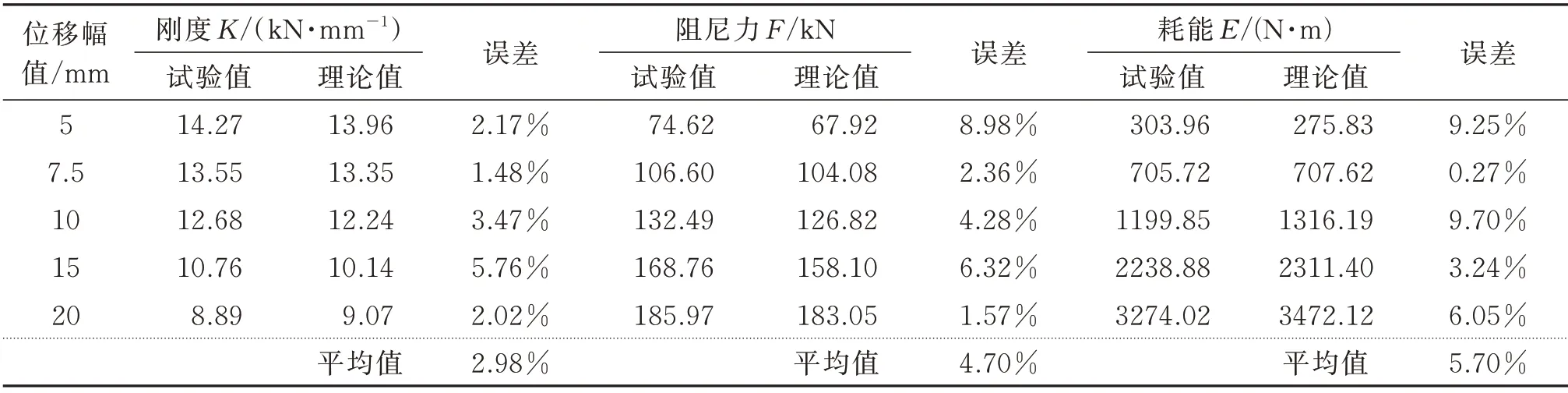
表5 位移放大型阻尼器试验值和理论值对比Tab.5 Comparison of experimental and theoretical values of displacement‑amplified dampers

为研究位移放大型黏弹性阻尼器的减震效果，分别对原框架结构（Original Frame Structure，OFS）、采用普通黏弹性阻尼器的减震结构（Visco⁃elastic Damping Structure，VDS）、采用附加2.5 倍位移放大装置的黏弹性阻尼减震结构（Viscoelastic Damping Structure with Displacement Amplification Device，AVDS）进行动力响应分析。阻尼器布置方案如图10 所示。两种方案阻尼器布置位置相同。在1～10 层沿X方向，每层布置4 片，共40 片，沿Y方向，每层的边跨布置2 片阻尼器，共40 片。不同方案的阻尼器参数如表6所示。

图9 位移放大型阻尼器曲线拟合的对比Fig.9 Comparison of fitting curves of displacement⁃amplified dampers

图10 阻尼器布置图Fig.10 Damper layout

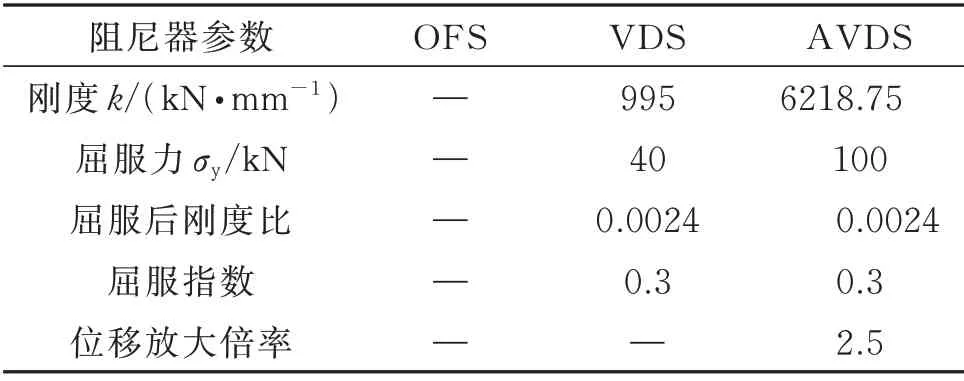
表6 阻尼器参数表Tab.6 Damper parameters

黏弹性阻尼器同时具有刚度特性和阻尼特性，因此结构自振周期有所减小。表7为结构在三种不同方案下的自振周期。由表中数据可得，框架结构在加入阻尼器及附加放大装置的阻尼器后，结构的第1 阶自振周期由未使用阻尼器时的1.135 s 减少到0.952 s。

表7 结构自振周期Tab.7 The structural natural vibration period

3.2 减震效应分析

图11（a），（b）给出了不同布置方案下平均层间位移角的对比。AVDS 系统的层间位移角较VDS系统在X向和Y向结构减震率分别提高2.26 倍和2.10 倍。其中，VDS，和AVDS 的减震结构的层间位移在X向的平均减震率分别为23.98%，54.18%，在Y向的平均减震率分别为22.98%，48.41%。

图11（c），（d）给出了不同布置方案下结构层间剪力对比结果。为考察结构本身的地震受力情况，此处呈现的剪力数据为结构梁柱的层间剪力，未考虑阻尼器出力对结构剪力的贡献。即结构梁柱层间剪力=结构总剪力−阻尼器出力。AVDS 系统的层间剪力较VDS 系统在X向和Y向的结构减震率分别提高2.05 倍和2.17 倍。其中，VDS 和AVDS 的减震结构的层间位移在X向的平均减震率分别为22.58%，46.31%，在Y向平均减震率分别为22.71%，49.12%。

图11 多遇地震下结构层间位移角及结构层间剪力比较Fig.11 Comparison of drifts and shear forces under frequent earthquakes

3.3 位移放大型黏弹性阻尼器耗能分析

表8给出了不同地震动作用下VDS 和AVDS的耗能分析结果。附加2.5 倍位移放大装置后，AVDS 的刚度、阻尼力和耗能显著提升。其中，阻尼器最大阻尼力平均放大2.97 倍，最大刚度平均放大2.89 倍，阻尼器耗能平均放大1.98 倍。

表8 阻尼器耗能分析结果Tab.8 The analysis results of damper energy consumption

表9给出了不同工况下结构的附加阻尼比分析结果，相比VDS 结构，AVDS 结构的附加阻尼比在X向提升2.8 倍，在Y向提升2.7 倍。VDS，AVDS模型的X向附加阻尼比平均值分别为6.90%，19.27%；Y向分别为8.40%，22.71%。

表9 附加阻尼比的对比Tab.9 Comparison of additional damping ratios

图12 给出了位于结构第3 层的阻尼器在不同地震动作用下的滞回曲线，AVDS 系统的耗能能力显著大于VDS 系统。多遇地震作用下，AVDS 系统即可发挥出可观的耗能减震效果，结构附加阻尼比最高可达到20%以上。位移放大型黏弹性减震系统在小震下即可进入工作状态，提供稳定的耗能能力，增强结构的抗震安全性。