多方向实车振动路谱对电池容量和阻抗特性影响的试验研究

2022-09-03周明博曹军义邹忠月

振动工程学报 2022年4期

周明博，曹军义，邹忠月

（1.西安交通大学机械工程学院，陕西西安 710049；2.河南速达电动汽车科技有限公司，河南三门峡 472100）

引言

动力电池作为电动汽车的关键能量来源，实现其可靠的性能监测对保障行车安全性至关重要，在对电池进行健康状态（SOH）估计［1⁃3］的研究中，容量和内阻作为直接指标得到了广泛关注。YU 等［4］将容量和开路电压均视为状态量，并基于戴维宁模型参数辨识对其实现联合估计，避开了总容量和荷电状态相互影响的问题。LU 等［5］发现了分数阶模型的阻抗阶数和电池循环次数存在着稳定的单调关系，从而可以采用分数阶评估电极老化。此外，对在线辨识所得内阻进行定量分析，进而实现故障诊断的方法也逐渐受到了重视［6⁃8］。

然而，为保证对动力电池上述状态指标进行监测的可靠性，全面考虑其影响因素是不可或缺的工作基础。除了温度等常规因素，车用动力电池在复杂服役环境下面临道路不平整、车辆加减速及转弯、碰撞等引起的多种振动情况，促进着相关研究越来越多地考虑振动对电池性能的影响［9⁃11］。

现有考虑电池振动测试的研究中，对象多集中于电池单体，并且分为三大类：（1）振动下电池的动力学响应，如Berg 等通过试验模态分析揭示软包和棱柱形单体的固有频率、阻尼比等随电池荷电状态（SOC）、SOH、温度的变化特征［12⁃13］，结果可为相应的振动安全测试提供支撑。（2）振动前后电池的特性参数变化，如文献［14⁃15］均采用SAE J2380 标准对单体进行测试，发现振动后电池内阻明显增加并伴随一定的放电容量减少。杨丽杰等［16］在GB/T 18287—2000 的基础上增加振动强度，并对振动后的单体进行循环寿命测试，表明振动会加速电池老化。 Yoon 等［17］采用ISO 17546 中正弦激励和NASA 随机振动参数对自行设计的串并联结构进行测试，根据振动后的电池内阻等参数变化表明构建电池模型时考虑振动因素的必要性。（3）振动中放电对电池参数的影响，如LI 等［18］使用10 Hz 以下的随机振动模拟行驶过程中的振动条件用以探究振动放电对电池单体剩余寿命预测的影响，并在文献［19］中表明6 自由度振动应力测试下电池欧姆电阻明显增大，并伴随放热增加和容量衰减。

综上，振动环境会对电池状态估计中的特性参数产生直接影响，而相关振动测试研究在振动参数、振动层级以及机械⁃电耦合测试上并没有较为统一的标准或规范，并且现有研究多基于电池单体测试，没有充分考虑单体成组挤压力与安装预紧力对激励传递的影响，缺乏对实车电池组振动性能的实验分析。

本文以电池模组为研究对象，通过分析国内外电池振动测试标准，提出采用多方向实车振动路谱对电池模组进行设计工况下的机械⁃电耦合测试方法来探究容量和阻抗性能影响。首先，采集实车道路谱下的电池包三向振动加速度，然后对原始数据进行频谱分析，选取能量集中频率区间分段拟合以获得适用于一般振动台的随机振动参数，最后搭建控温环境下的振动放电试验系统，以电池模组为对象还原实车中的安装形式与预紧力，设计相应测试工况，探究振动条件对可用容量和阻抗特性的影响。

1 多方向实车振动路谱提取

1.1 振动测试参数规范性分析

总的来看，针对动力电池的绝大部分安全性测试规范已经把振动列入了测试内容。归纳后可以作为原始参考标准的有USABC 1996，UN 38.3，IEC 62660⁃2（3），ECE R100⁃02 和中国的GB/T 31486—2015 五项内容，上述标准常被直接用于探究振动对电池性能影响的测试，但较为突出的问题表现在：

（1）现有标准多为抗机械滥用性测试，在振动参数上并不适用于探究振动对电池性能影响的测试。

例如，一方面，ECE R100⁃02—2013 和GB/T 31486—2015 仅对垂向的测试做了说明，前者采用7～50 Hz 扫频振动且最大加速度值仅为1g，后者采用10～55 Hz 和最大加速度为3g的扫频振动。另一方面，考虑多方向测试的标准中，UN38.3 着重于锂电池运输安全，按重量12 kg 以下和12 kg 以上分别制订参数，采用7～200 Hz 最大振幅0.8 mm 的扫频振动进行测试；IEC 62660⁃2（3）采用的随机振动最高频率达到2000 Hz；USABC 1996 在适合于安装电池的位置进行道路行驶下振动采集，按照累积数据指出10～30 Hz 为共振区间，加速度整体小于5g，实际仍未直接对电池包振动量进行获取。

（2）现有标准大多没有考虑机械⁃电耦合测试，并不符合电池服役环境。

上述标准中，仅有中国的GB/T 31486—2015明确提出了“振动同时需要进行放电测试”的要求，具体为：从满电状态以的电流进行放电并观察有无异常。

综合上述分析，现有振动测试标准仍不能满足相关研究的需求。探究电池性能受振动影响时，往往是期望用于电池状态估计和故障诊断，然而，不同的车型、电池包安装形式以及电池成组形式往往对应着不同的激励传递效果。文献［20⁃21］在讨论相关振动测试标准时同样提出电池包的振动标准应根据电动汽车在一般道路上的行驶路谱制定。因此，为了有针对性地考虑不同测试对象的激励传递特点，同时符合实际机械⁃电耦合服役工况，需要采集多方向实车路谱，并规范振动参数提取方法，进而完善电池容量和阻抗特性受振动影响的相关试验研究。

1.2 实车道路下的振动激励与响应

本次电池包振动信号采集所用车辆为一辆状况良好的某型号轿车，整备质量1.4 t，乘坐两人约140 kg 进行路谱测试。选用型号为CXL25GP3 和CXL10GP3 的两个三向加速度传感器分别用于汽车后摆臂和电池包底部振动加速度信号的室外路面测量，连接型号为NI USB⁃6002 的采集卡，通过Labview 上位机程序将数据存入电脑中，后摆臂处测点主要用于等效路面激励并与电池包振动信号进行对比分析。

加速度传感器在电池包底部和车轮后摆臂处的固定位置如图1（a）和1（b）所示。

图1 三向加速度传感器位置Fig.1 Position of acceleration sensors

车辆受平坦路面激励产生的振动量较小，因此需要选择强化路谱来再现可能面临的恶劣工况，文中数据采集选用的各强化试验道路如图2所示。

图2 试验道路Fig.2 Testing roads

结合道路模拟试验中路谱采集相关规范，经过长波路和扭曲路时分别控制车速在20 km/h 附近和怠速状态，其余特殊道路控制车速在30 km/h 附近。以其中一组测试为例，经过各强化路段时的电池包和后轮摆臂上加速度信号分别如图3和图4所示。垂向、纵向和横向幅值信号为同一时刻采集所得，按照经过的路段顺序划分为7 个区间，依次为石块路、搓板路、平坦路面、长波路、卵石路、鱼鳞坑路和扭曲路。

图3 电池包加速度信号Fig.3 Acceleration signal of battery pack

从图3和图4可以看出：（1）后摆臂上的振动响应远大于电池包上的响应，在鱼鳞坑路段峰值加速度最大能够达到20g，而电池包上的振动均在2g以下，说明从路面到电池包的振动能量传递受到了明显抑制。（2）对比两图不同方向的振动加速度幅值大小，发现摆臂垂向加速度最大，但如图3所示，除缓慢行驶的长波路和扭曲路之外，电池包的水平加速度在多种路况下同样较大，尤其是经过搓板路时的纵向加速度最大，表明电池包对激励的敏感方向不同。分析出现该情况的原因与电池包吊耳分布和安装时的连接形式有关，例如连接处对横向剪切应力敏感程度高于纵向拉伸方向等。

图4 后摆臂加速度信号Fig.4 Acceleration signal of rear swing arm

正是基于此类情况，才更需要采用普适性的方法针对特定车型和电池包安装形式基于实车路谱进行多方向振动分析，以便为性能探究提供有效支撑。

1.3 振动路谱参数提取方法

由于一般车辆行驶中电池包通常更容易受到道路不平整带来的垂向激励，因此在对比各特殊道路下电池包垂向功率谱密度能量分布后，选择垂向振动能量最大的鱼鳞坑路为例进行处理。加速度时域波形如图5（a）所示，对其进行PSD 计算，截取100 Hz 以下功率谱密度分布如图5（b）所示。

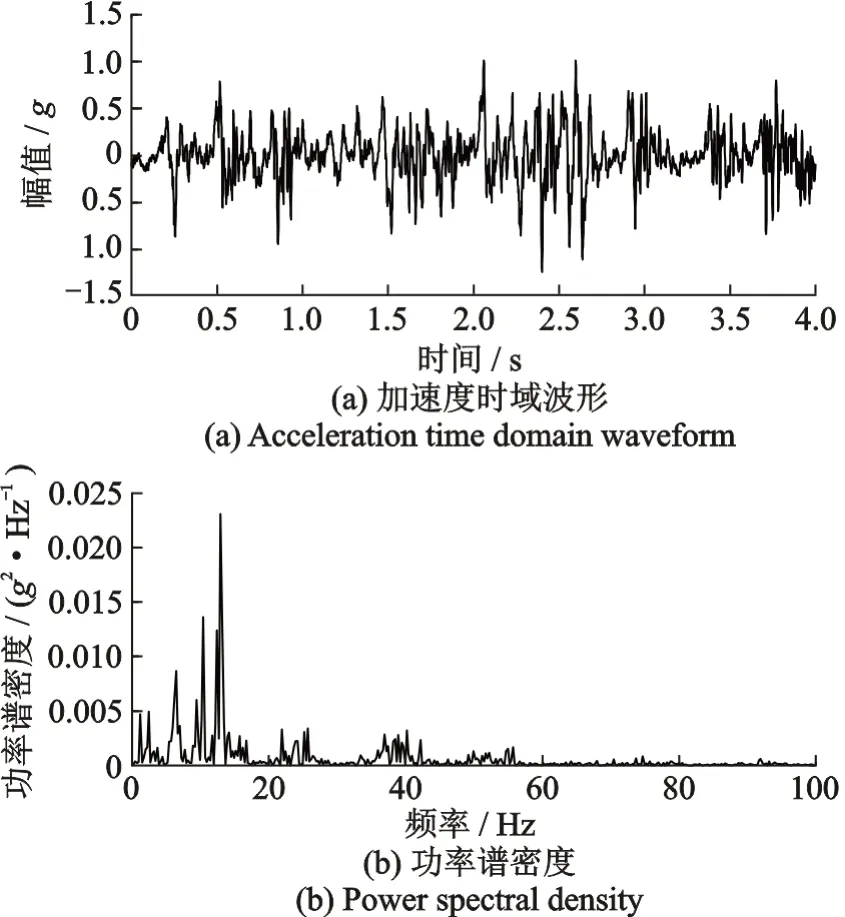
图5 电池包鱼鳞坑路段垂向信号Fig.5 Vertical signal of fish scale pit for battery pack

依据所求功率谱密度估计的分布，积分并开平方获得0～100 Hz 加速度RMS 的值为0.2664g，0～50 Hz 加速度RMS 的值为0.2463g。结合图5频域分布，明显地，振动能量主要集中于低频范围内，本研究中选取0～50 Hz 功率谱密度分布用于设计随机振动输入参数。

利用实验室振动台控制随机振动时，需要手动输入节点参数，即频率⁃功率谱密度参数，因此需要依据上述功率谱密度分布进行分段近似处理，在尽量减少能量损失的条件下，依据频域内能量分布获取对应关系。所得频域内能量和频率段对应关系如表1所示。

表1 频域内能量分布Tab.1 Energy distribution of frequency domain

由于一般实验室电动振动台无法工作在0 Hz附近，且最低工作频率为5 Hz，因此忽略0～5 Hz 范围能量，按照表1能量分布，分段近似获取随机振动参数曲线如图6所示。按照该振动参数曲线积分得到总能量为6.42（m/s2）2，相应地，由表1可得原始的鱼鳞坑路段功率谱密度估计曲线的总能量为6.07（m/s2）2，二者差值为0.35（m/s2）2，则表明当前构造的随机振动输入参数在能量满足频域分布的同时无明显损失或超差。

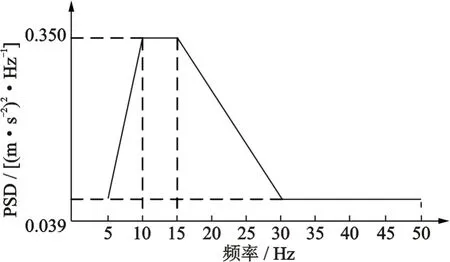
图6 随机振动输入参数Fig.6 Parameters of random vibration

2 多方向路谱振动下电池特性试验

依据上述所得路谱下的随机振动参数，探究实测振动环境对该车辆搭载的某型号动力电池放电性能的影响。

2.1 振动测试试验平台

为了提供所获取的随机振动测试条件，同时避免振动之外其他温度变量等的影响，搭建电池振动放电试验系统如图7所示，当前振动台的工作状态为垂直方向。其中，电池组充放电功能由型号为RCDS⁃60V400A⁃T 的Repower 电池测试系统实现，各单体电池的温度、电压采集由多通路温度电压采集仪完成，温度监测范围为-20～100 ℃、测量精度为±1 ℃，单路电压监测范围为±5 V、测量精度为±5 mV；环境温度控制功能由重庆哈丁可程式温度湿度环境箱实现，箱体底部的软胶皮盖门位于固定工装与振动台面之间，实现相对密闭环境；振动控制部分由电荷型加速度传感器及振动采集控制仪、东菱振动台（型号为ES⁃20⁃320）、振动控制柜和高压气源组成。

图7 振动测试试验台Fig.7 Platform of vibration testing

为充分还原动力电池在实车中的受力情况（不改变电池单体的成组挤压力和模组安装预紧力），选择搭载于该车型的方壳电池模组作为测试对象，并设计相应固定工装以复现模组在箱体中的固定形式，保证振动激励能够准确可靠地传递到电池。环境箱中的电池模组和固定工装的形貌如图8所示，模组由四周螺栓按照标准扭矩固定，底部垫有软泡棉代替硅胶垫。

图8 电池模组和固定工装Fig.8 Battery module and fixture tools

2.2 振动测试工况

测试所用的模组由9 块电池单体串联构成，模组尺寸为490 mm×177 mm×144 mm，额定容量为120 Ah，工作电压范围为27.00～38.25 V。

所有测试采用环境箱控温25 ℃，首先进行静态下（无振动）的标准充放电测试，得到静态容量，以便于和振动放电容量进行对比。以图6中的随机振动曲线作为统一振动参数，探究振动对容量和内阻影响的具体测试方案如图9所示，按照该方案依次完成X，Y，Z三个方向的测试。其中，标准充电采用0.5C转0.1C、恒流转恒流充电，以单体最高电压4.25 V 为截止条件，标准放电采用1C恒流放电，以单体最低电压3.0 V 为截止条件。

图9 容量和阻抗影响测试方案Fig.9 Testing scheme of capacity and impedance

“脉冲放充”定义为：以2C的电流放电10 s，静置40 s，以2C的电流充电10 s。按照“压降/电流”的方法计算不同SOC（90%，70%，50%，30%，10%）下的直流内阻，并将1 s 直流内阻作为欧姆内阻R0，将10 s 直流内阻记为R10。直流内阻计算公式为：

值得注意的是，容量测试的每一次振动放电后，要有>2 h 的静置时间，以保证电池温度恢复和避免振动对下一次充电电量产生影响；同样地，内阻测试中放电至指定SOC 后也要有相应的静置时间。

2.3 容量和阻抗特性

按照上述测试方案，得到静态测试和不同方向下的振动放电容量对比如图10 所示，具体容量值统计于表2中。三次静态容量测试中最大值为120.82 Ah，最小值为119.51 Ah；振动容量测试中，X方向最大值为120.06 Ah、最小值为119.6 Ah，Y方向最大值为120.45 Ah、最小值为120.06 Ah，Z方向最大值为120.63 Ah、最小值为120.3 Ah。按照GB/T 31486—2015《电动汽车用动力蓄电池电性能要求及试验方法》规定，蓄电池模块初始容量测试连续3 次试验结果的极差小于额定容量的3%，可提前结束试验。明显地，本次容量测试中，各种情况下容量极差约为1%，则表明：实测路谱下的该振动条件对放电容量并无明显影响。

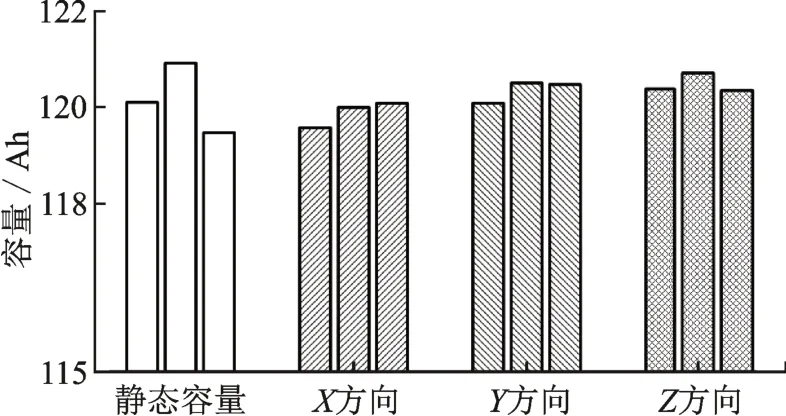
图10 振动下放电容量Fig.10 Capacity of discharge under vibration

表2 放电容量统计Tab.2 Statistics of discharge capacity

内阻测试结果中，按照9 个单体×5 个SOC 点，则每个方向有45 个欧姆内阻值和45 个10 s 直流内阻值。按照数据统计特性初步分析振动对内阻的影响如表3所示，可以看出：45 组数据中，与静态内阻相比，各振动方向下的10 s 直流内阻均表现为增大，而欧姆内阻中有少数表现为减小（具体为X方向有2 组数据中内阻未增大，Z方向有1 组数据内阻未增大），在试验中不能排除少数异常值是短时计算偏差导致，因此将振动引起内阻增大的次数除以总测量次数作为置信度，则依据统计结果在各方向上能够以95%的置信度认为振动会引起内阻增大。

表3 振动引起的内阻变化统计Tab.3 Statistics of impedance variation caused by vibra‑tion

为了便于全面直观地表达振动环境下放电对电池阻值的影响，在此计算9 个单体的平均内阻，对比各方向振动与静态情况下脉冲阻值变化情况如图11 所示。整体来看，平均内阻随SOC 的变化趋势同样符合先减小后增大的规律，并且在低荷电状态时振动引起的阻值增大趋势更加显著。

图11 不同振动方向对内阻的影响Fig.11 Effects on impedance of different vibration directions

为了采用直接的量化指标探究振动对内阻的影响，内阻增长率的计算式为：

并将结果统计于表4中。

由表4的计算结果可以看出，针对平均内阻进行分析，所有振动测试均造成动力电池内阻增大，并且10 s 直流内阻增大趋势更加明显，具体表现为欧姆内阻增长率处于1.6%～8.0%，10 s 直流内阻增长率处于2.1%～8.7%。并且，在荷电状态为10%的情况下，除了X方向的欧姆内阻，各方向振动均引起了约8%的内阻增大，电池低荷电状态时的内阻受振动影响程度大的趋势十分明显。考虑部分电池类型以内阻作为指标进行健康状态估计时的内阻增长率一般与容量衰减率相符，约为20%，因此进行相关在线分析与诊断时，必须要考虑振动对内阻的影响。

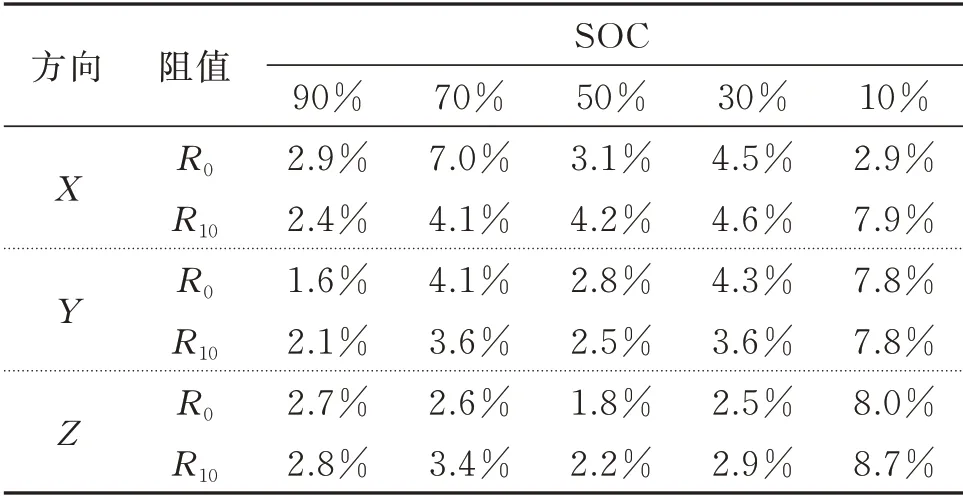
表4 振动引起的内阻增长率Tab.4 Growth rate of impedance caused by vibration

综上，采用实车路谱下采集的电池包振动信号作为输入，以实车电池真实模组为实验对象，可以保证电池成组形式和挤压力符合实际工作状态。严格按照车内电池模组的安装与固定形式以及预紧力等进行了试验台架搭建，对振动激励在实验室做到尽可能的还原，并且采用恒温箱排除温度对容量和内阻测试的影响，所以能够认为针对该型号电池组的振动放电测试结果可靠，即一般的路面振动对容量影响不明显，但会造成内阻不超过10%的增大。然而，在探究振动对电池性能影响的研究中，针对不同车型，不同的车身重量、悬架系统、电池包安装位置、安装形式、包内电芯成组形式等很难有统一的标准振动参数来评价或者等效为实际道路对该车型电池的激励情况，也就难以有针对性地进行实车振动环境下健康状态评估。因此，本文提出的基于多方向实车路谱提取随机振动参数并进行动力电池振动放电测试的方法能够为考虑振动因素的动力电池状态估计与故障诊断提供支撑。