含惯容和接地刚度的黏弹性动力吸振器的参数优化
2022-09-03范舒铜申永军
范舒铜,申永军,2
(1.石家庄铁道大学机械工程学院,河北石家庄 050043;2.石家庄铁道大学省部共建交通工程结构力学行为与系统安全国家重点实验室,河北石家庄 050043)
引 言
动力吸振器(dynamic vibration absorber,DVA)是通过调整主系统的振动特性以减小主系统振动的设备[1]。Frahm[2]发明了第一个适用于窄频带范围的无阻尼动力吸振器。Ormondroyd 等[3]在无阻尼动力吸振器的基础上增加阻尼,发现了减振效果更好的动力吸振器模型,即经典的Voigt 型动力吸振器。他们首次提出了固定点理论,被后人广泛地应用并且成为了振动工程教科书[4⁃5]中的经典结论。随后,Asami 和Nishihara 等[6⁃8]提出了有阻尼动力吸振器的精确级数解,验证了固定点理论的正确性。Ren[9]提出了一种减振效果更佳的接地式动力吸振器。文献[10]利用另一种方法也推出了与文献[9]相同的结果。Shen 等[11⁃12]研究4 种半主动动力吸振器的近似解析解,并分析了半主动动力吸振器的参数设计和时滞对半主动控制效果的影响。
随着实际工程研究的逐渐深入,黏弹性材料的使用给各个领域提供了更大的发展空间。黏弹性材料的模型一般可简化为Kelvin 模型或者Maxwell 模型。在实际工程中,阻尼器本身一般具有一定的弹性,故Maxwell 模型更能代表工程实践中的黏弹性材料[13]。王孝然等[14⁃15]和郝岩等[16]将Maxwell 模型应用到动力吸振器中,极大地降低了共振幅值,同时拓宽减振频率。
具有放大功能的元件如杠杆、惯容等也被应用在吸振系统中,以获得更好的性能。惯容最早应用在F1 赛车悬架上,并取得了很好的效果[17]。Wang等[18]将惯容器应用到列车悬挂系统,可以有效地提升列车的动力学性能。Chen 等[19]分析了惯容器对隔振系统固有频率的影响。Hu 等[20⁃21]把惯容用在动力吸振器和隔振器上,并给出了最佳设计方案,结果表明惯容有很好的减振效果。Yang 等[22]研究了ISD(I——惯容,S——弹簧,D——阻尼)结构在双层隔振系统中的性能,表明ISD 在一定的频率范围内有很好的减振效果。葛正等[23]提出了车辆主动惯容式动力吸振悬架构型和车身加速度补偿控制策略。文献[24]也证明了ISD 结构具有很好的减振功效。陈杰等[25]将惯容器和负刚度弹簧引入到动力吸振器来抑制梁的横向振动,具有显著的减振效果。近年来,Giaralis 等[26]和Xu 等[27]分别研究了含惯容的动力吸振器对高层建筑和大跨桥梁风致振动的控制效果。文献[28]研究了旋转惯质双调谐质量阻尼器对光热电站吸热塔横风向与顺风向风致振动的控制效果。李亚峰等[29]将惯容加入到动力吸振器,通过不同模型的对比分析减振性能。文献[26⁃29]都表明惯容可产生远大于其物理质量的表观质量,在减振方面有着明显的优势。
惯容元件自身具备惯性调整功能,改变结构惯性的同时基本不改变结构的物理质量。黏弹性器件和惯容器同时用于动力吸振器的设计,可提高系统的控制性能,但目前的大多数研究仅仅在动力吸振器中引入惯容器或黏弹性器件。少数研究同时引入了惯容器和黏弹性器件,但惯容接地,本质上是增加了子系统的质量,未能体现惯容的两端点特征。
基于惯容和黏弹性器件的优良特性,本文提出一种惯容器和黏弹性器件共同作用的动力吸振器,利用固定点理论将系统的刚度比、阻尼比等参数进行优化处理。在参数优化过程中,发现黏弹性器件和惯容器共同作用时,惯容比在一定的范围内存在两组优化参数。考虑实际工程应用并保证系统的稳定,常规参数下比较两组优化参数对系统振幅的影响,确定惯容比的最佳工作范围。通过与传统的动力吸振器在简谐激励和随机激励下的比较,证明了恰当地选取惯容比可使含惯容和接地刚度的黏弹性动力吸振器具有较优的减振效果。
1 动力吸振器的模型建立及参数优化
图1所示为本文提出的含惯容和接地刚度的Maxwell 黏弹性动力吸振器的模型。其中m1,m2分别代表主系统和动力吸振器的质量;k1,k2分别代表主系统和动力吸振器的刚度;b代表动力吸振器的惯容;c和k3分别是Maxwell 型黏弹性模型的阻尼和刚度;k4表示接地弹簧的刚度,F0代表激振力的振幅,ω表示激振力的频率;x1,x2,x3分别表示主系统、动力吸振器以及串联弹簧和阻尼分割点的位移。
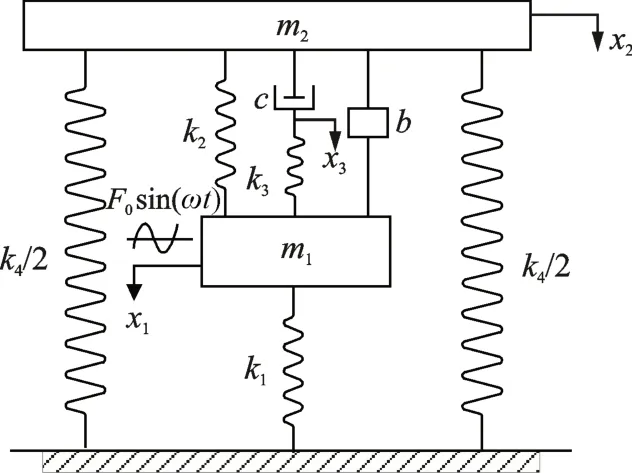
图1 动力吸振器模型Fig.1 Mechanical model of dynamic vibration absorber
根据牛顿第二定律可以得到系统的动力学方程:
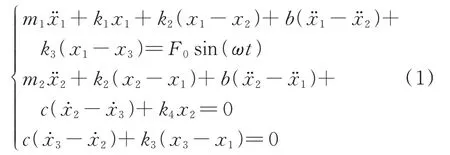
引入下列参数:
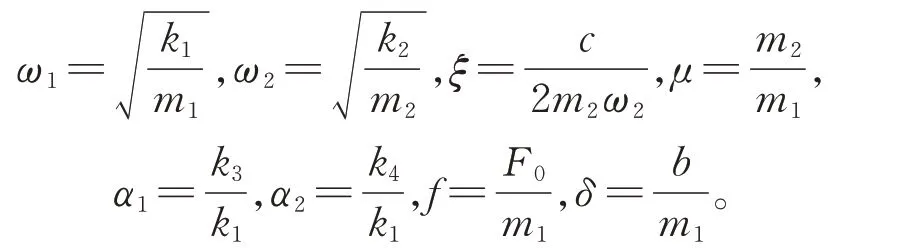
式(1)可以化简成如下形式:
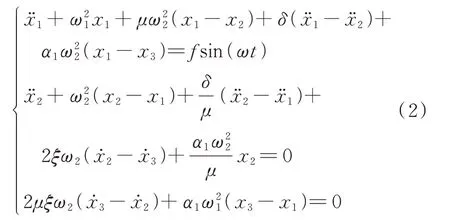
设式(2)解的形式为:

式中 j 为虚数单位。将式(3)代入式(2)中,可以解出:
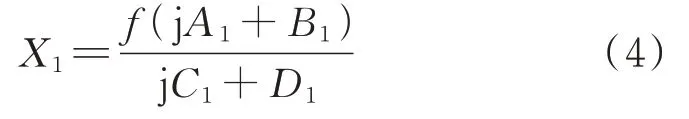
其中:
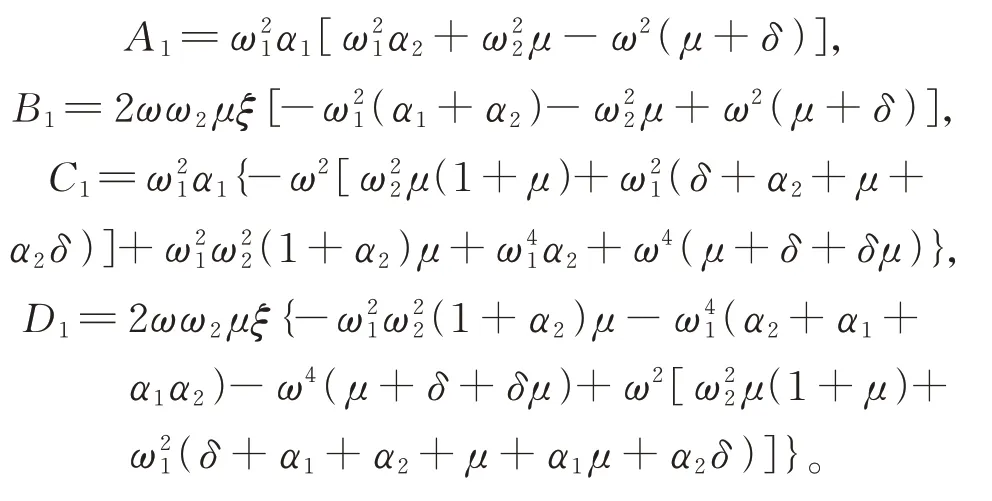
引入参数:

定义主系统的振幅放大因子A:
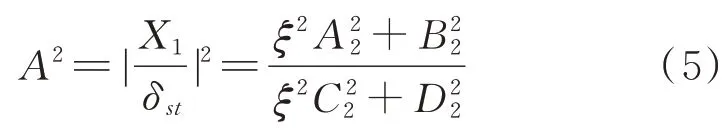
其中:
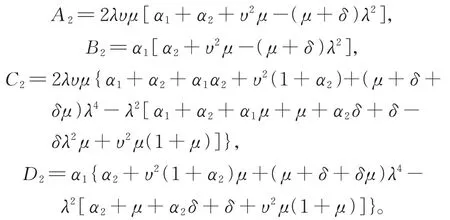
2 基于固定点理论的H∞参数优化
由式(5)通过简单推导,可以证明其归一化的幅频曲线都将通过3 个独立于阻尼比的点,这3 个点称为该动力吸振器的固定点。为了直观验证该结论,图2给出了阻尼比为0.9,1.5,2 时的归一化幅频曲线。从图2中可以清楚地看出曲线均通过P,Q,R三点。
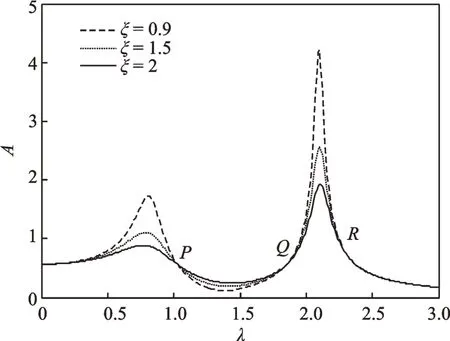
图2 μ=0.1,δ=2,υ=3.26,α1=6.76,α2=2.79 时不同阻尼比下归一化幅频曲线Fig.2 The normalized amplitude-frequency curves under dif⁃ferent damping ratios with μ=0.1,δ=2,υ=3.26,α1=6.76,α2=2.79
由于固定点与阻尼比无关,故根据固定点理论,若使三个固定点处的纵坐标相等,只要阻尼比趋于零和无穷时的响应值相等即可,则有:

化简得到:
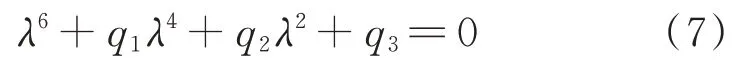
其中:

由于固定点与阻尼比无关,因此当ξ=0 时满足:

当ξ=∞时满足:

P,Q和R三点在ξ=0 和ξ=∞的幅频曲线上幅值大小分别相等,但相位均相差180°,即均相差了一个正、负号。所以为了求出P,Q和R三点的值,联立式(8)和(9)可以得到:
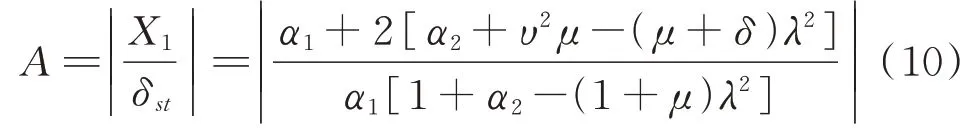
设和是式(10)的三个根,只要λp,λQ和λR的值确定,可以得到P,Q和R三点的纵坐标如下:

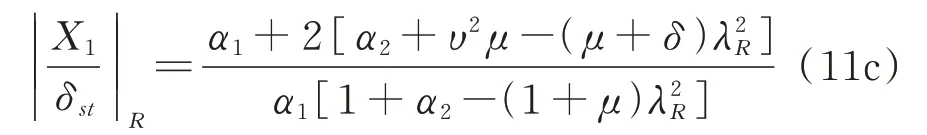
当把3 个固定点的纵坐标调到同一高度,就可以得到最优调频比,从而有可能使得幅频曲线的最大值最小化。这个调整需要两个步骤实现。
第一步,把P点和R点的纵坐标调到同一高度,即:
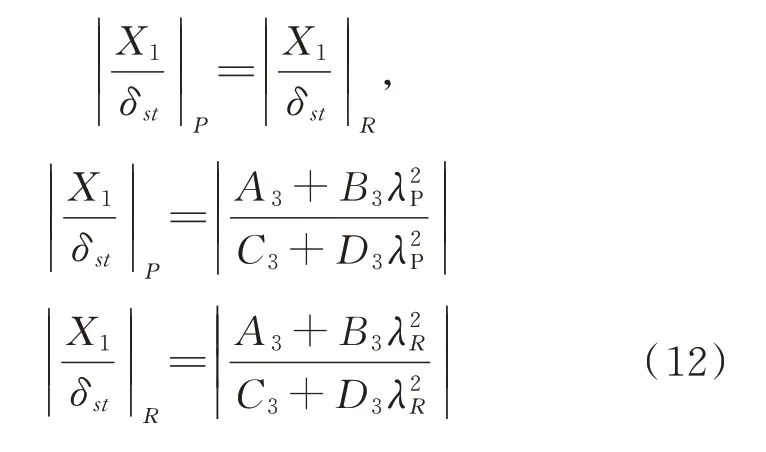
其中,

P点和R点的纵坐标相等时的值与λ2无关,则需要:
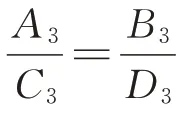
即:
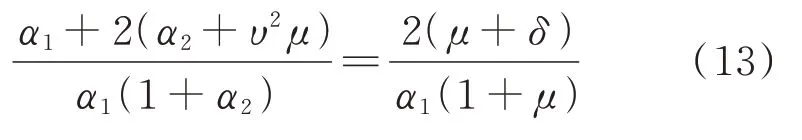
化简式(13),得:
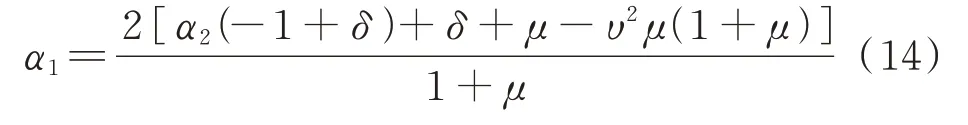
把式(14)代入式(7)中,可以得到:
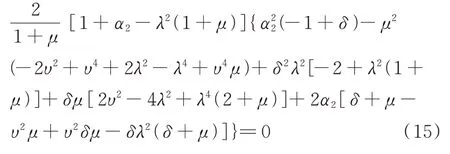
解式(15)得到:
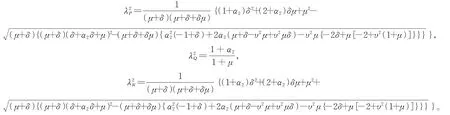
式(11)可以写成:
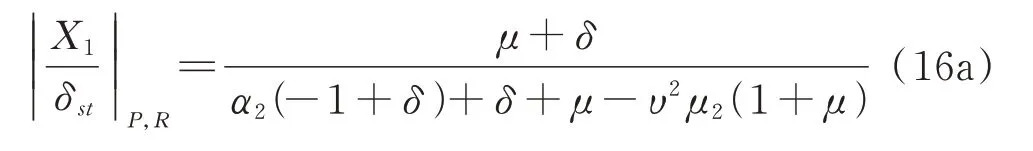
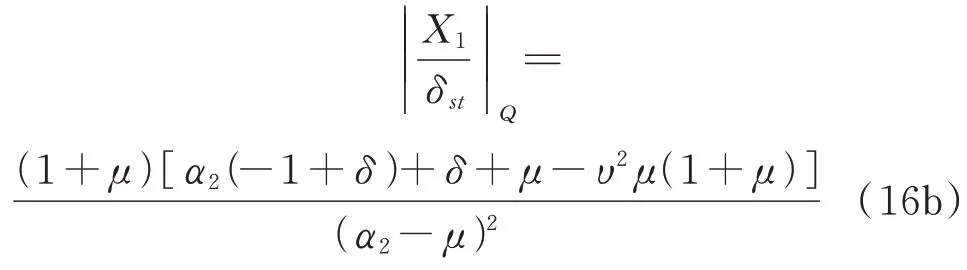
第二步,把P,R点与Q点的纵坐标调整到同一高度,可以得到最优频率比:
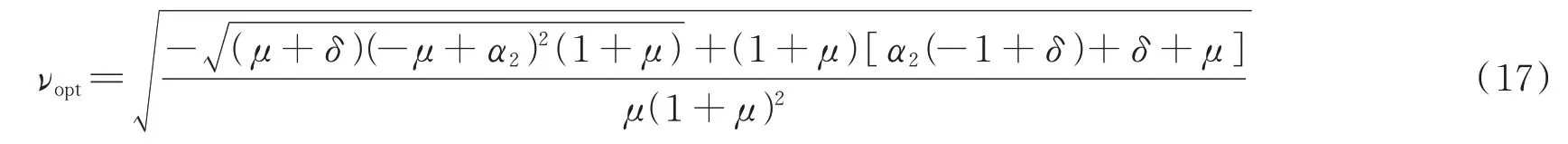
将式(17)代入式(14)得到:
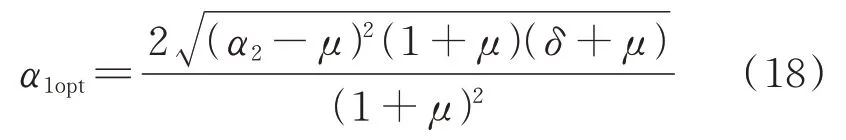
此时:
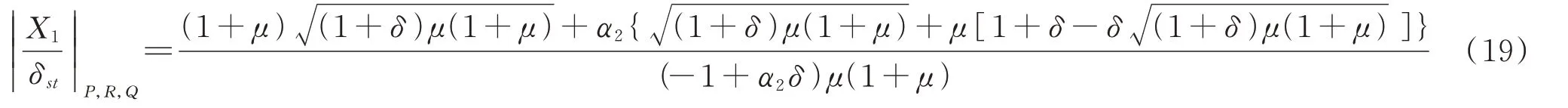
由于本文模型中的接地刚度可能是负刚度,根据负刚度器件的特性,预压缩弹簧或者预压连杆是实现负刚度特性的常见机构,而预加荷载会使系统产生预加位移,故不合适的刚度值有可能导致刚度矩阵非正定从而系统失稳。因此,本文按固定点算法得到可能的接地刚度比值后,进行系统稳定性的验证,并给出接地刚度比值的范围。下文通过对所求出的最优刚度比、最优频率比、最优阻尼比的验证,说明当预加荷载使系统产生的位移等于固定点处响应值时,所得结果可以在提高振动控制效果的同时保证系统稳定。因此有:
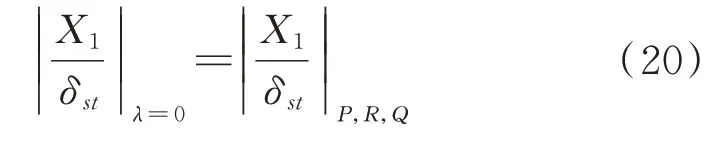
即:
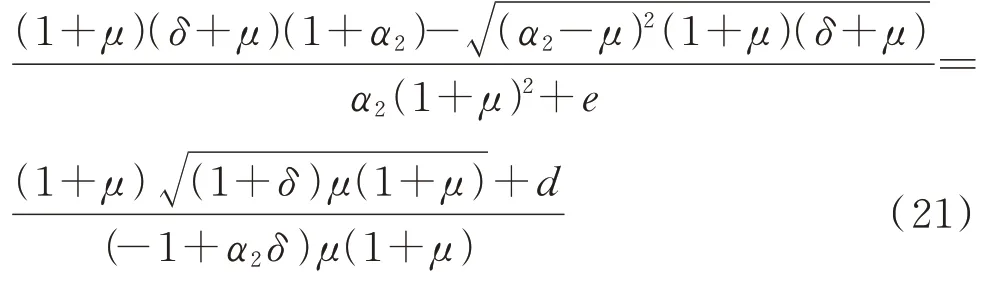
其中:
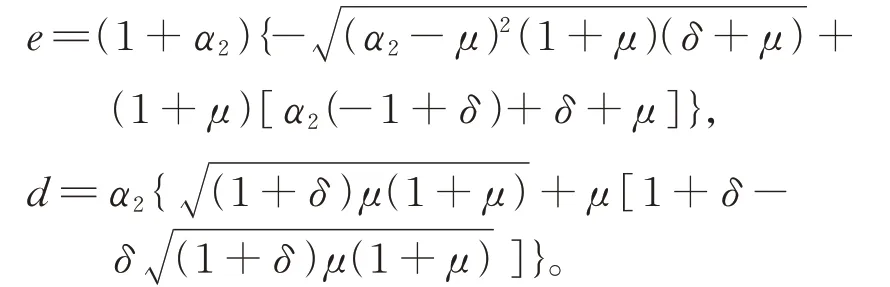
求解上式则可以得到所有可能的最优刚度比的值:

而系统的固有频率为:

其中:

固有频率是非负的,故可以得到:
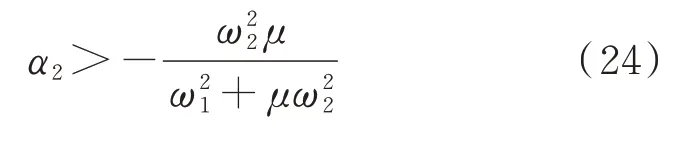
即:
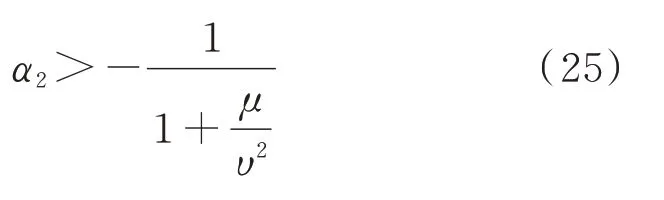

通过研究发现,当α2opt=α2a或α2opt=α2b时,惯容比均可在相对应的范围内使系统保持稳定并实现减振,故分情况讨论最优参数的选取情况,如下:
(1)当α2opt=α2a=时,
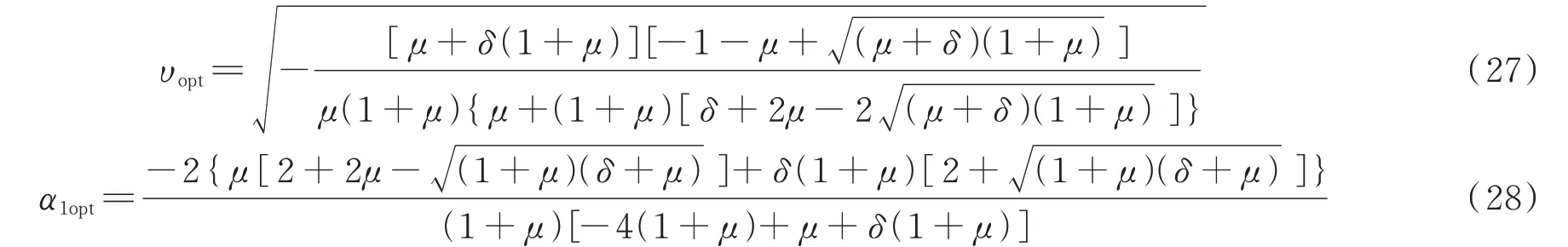
根据固定点理论可知,无论阻尼比怎么变化,都会经过P,Q和R三个固定的点,当两个共振峰调整到同一高度,便可以得到最优阻尼比。由图3可知,当两个共振峰处于同一高度时,Q点处的幅频响应曲线恰好处于斜率为零的区域。故可以根据Q点处的横坐标和极值条件求出最优阻尼比。
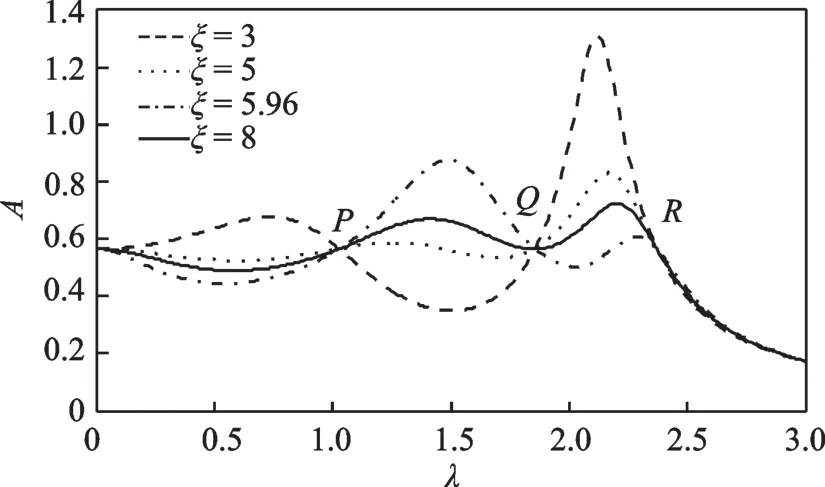
图3 μ=0.1,δ=2,υ=3.26,α1=6.76,α2=2.79 时不同阻尼比下归一化幅频曲线Fig.3 The normalized amplitude-frequency curve under differ⁃ent damping ratios with μ=0.1,δ=2,υ=3.26,α1=6.76,α2=2.79
根据
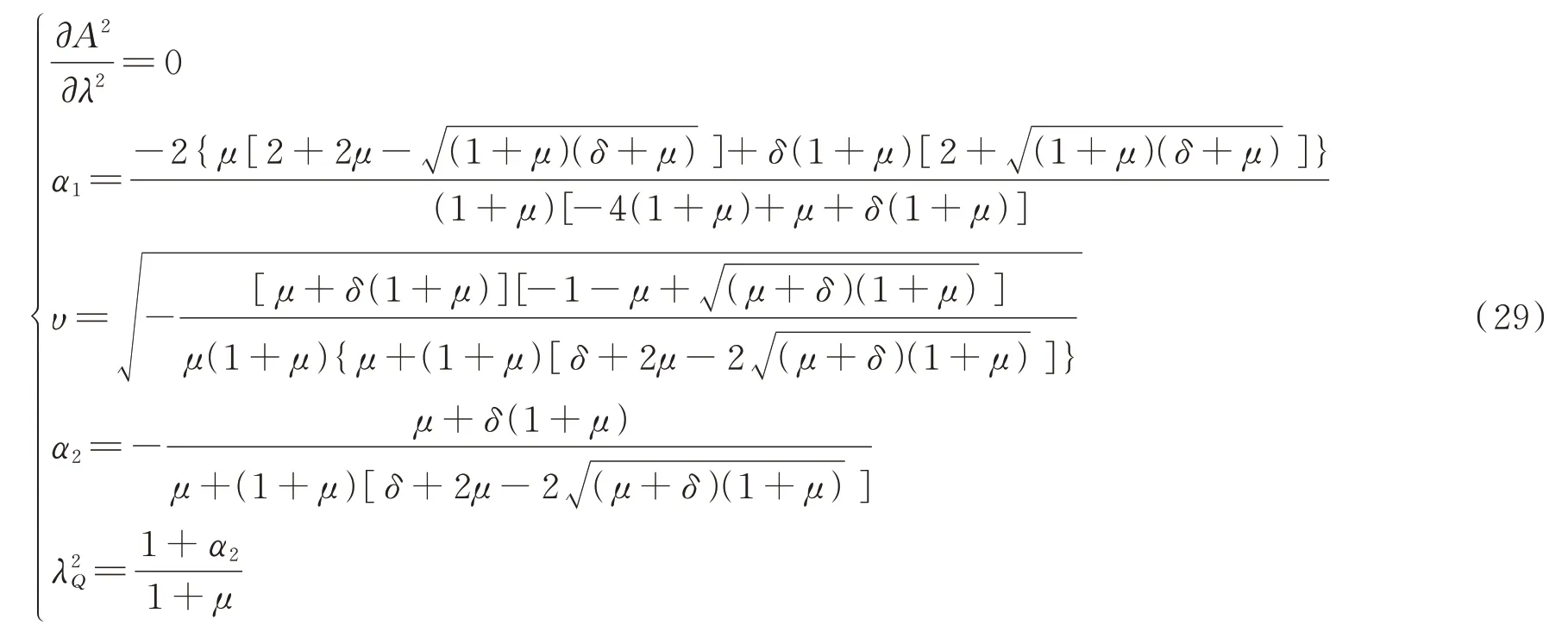
从而得到近似最优阻尼比:
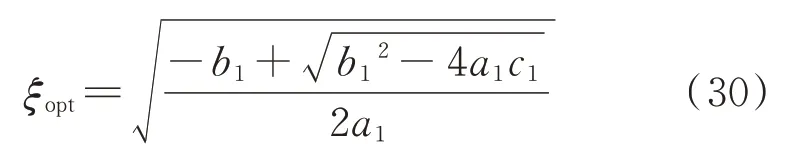
其中:
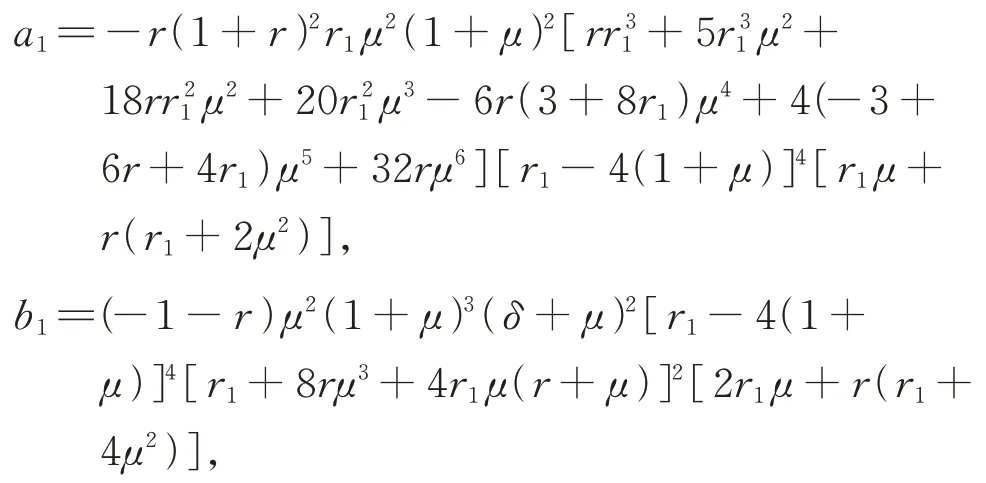
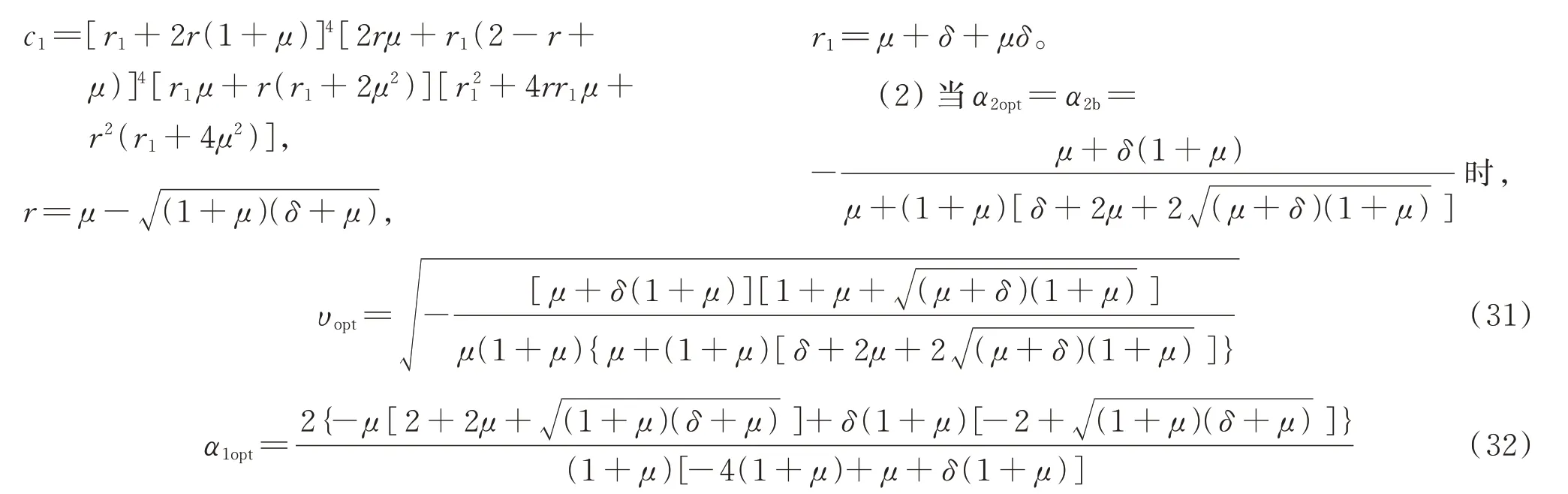
由图4可知,可以运用和上述同样的方法根据Q点处的横坐标和极值条件求出最优阻尼比。
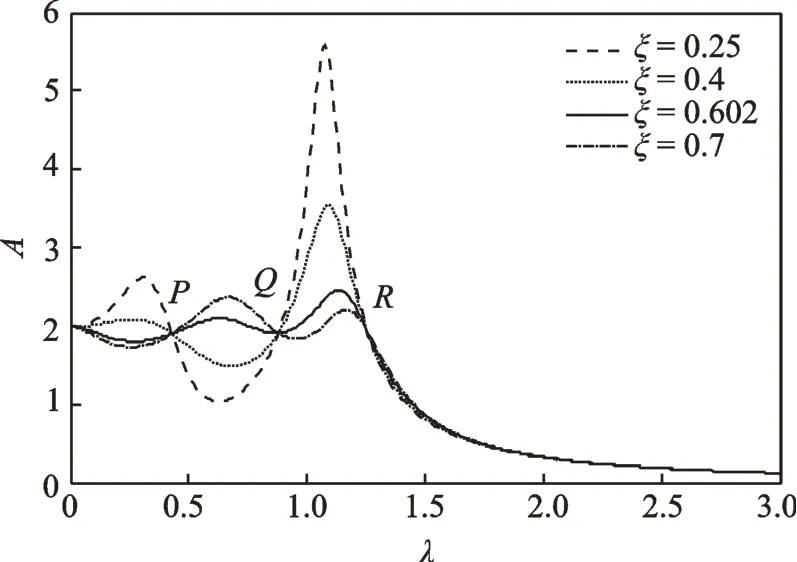
图4 μ=0.1,δ=0.1,υ=1.43,α1=0.189,α2= -0.145 时不同阻尼比下归一化幅频曲线Fig.4 The normalized amplitude-frequency curve under dif⁃ferent damping ratios with μ=0.1,δ=0.1,υ=1.43,α1=0.189,α2= -0.145
根据
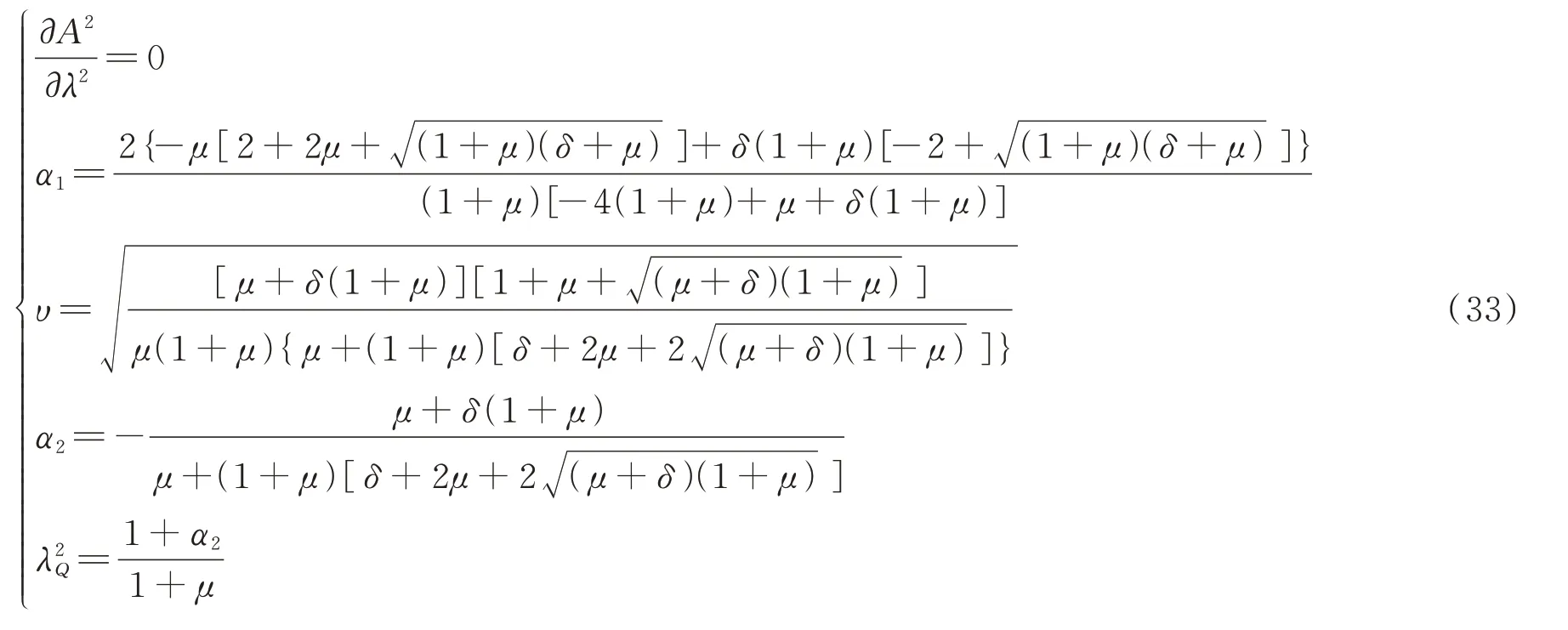
从而得到近似最优阻尼比:

其中

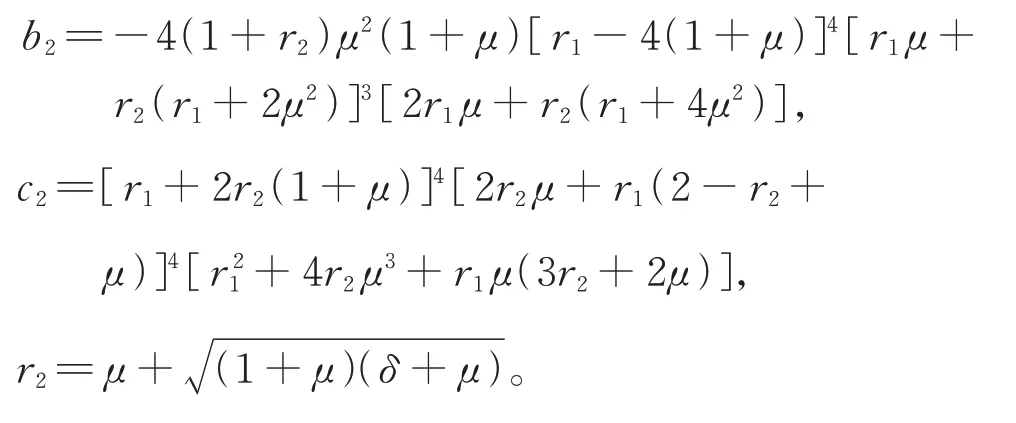
3 不同情况惯容比的工作范围以及最优参数的选择
在第2 节中已经验证了两组最优参数均满足系统的固有频率大于0,故在筛选最优接地刚度比α2opt时,只需考虑各最优参数及其求解过程,即惯容的工作范围应该同时满足各表达式分母不等于0,根号下部分大于0,最优频率比υopt和最优阻尼比ξ2opt大于0 的交集。
3.1 不同的α2 对应的惯容比δ 的取值范围
将α2a代入最优频率中去讨论惯容比δ的取值范围,即:
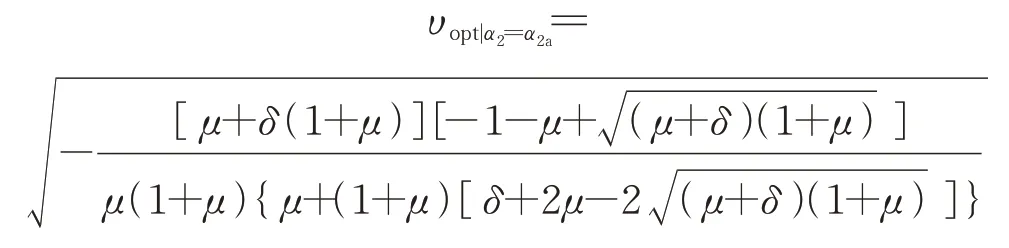
即满足:
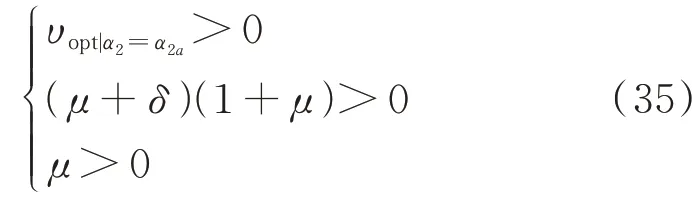
故简单筛选判定后,δ的取值范围即为:

其中:
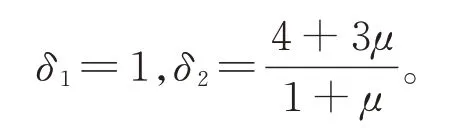
将α2b代入最优频率中讨论惯容比δ的取值范围,即:

即满足:

故简单筛选判定后,δ的取值范围为:

3.2 最优参数的选择
从3.1 节的分析中可知,不同的接地刚度比α2对应的惯容比δ的取值范围是不同的,故在实际工程中该模型的最优参数应该根据不同的惯容比进行选取。
当δ∈(0,δ1)∪(δ2,+∞)时,只有一个α2,即α2=α2b,那么就取α2=α2b及对应的最优参数——最优频率(式(31))、最优刚度比(式(32))和最优阻尼比(式(34))。
当δ∈(δ1,δ2)时,有两个α2,即α2=α2a或α2=α2b,此时可以根据固定点处的幅值进行分析。
当α2=α2a时,固定点处的幅值为:
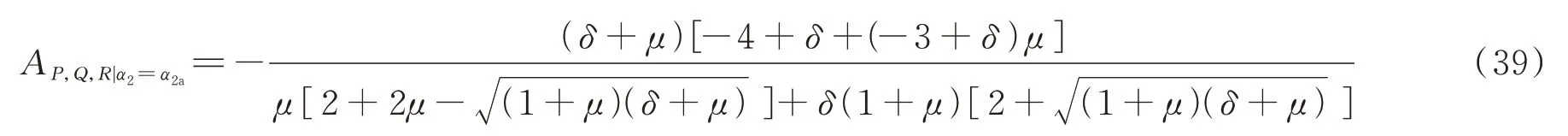
当α2=α2b时,固定点处的幅值为:
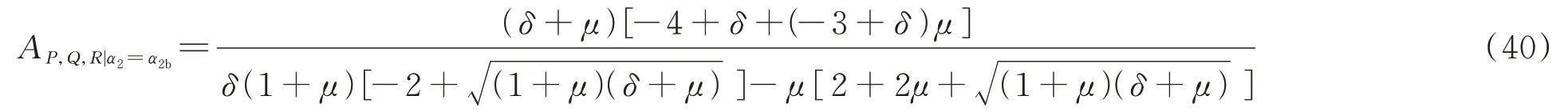
两个幅值作差:

从图5中可以看出在常规的参数范围内,即质量比μ∈(0.01,0.4)和惯容比δ∈(δ1,δ2)内都可以使得ΔA>0,因此:
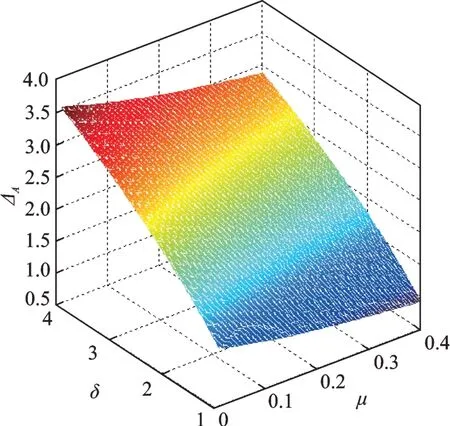
图5 不同质量比和惯容比下的幅值差Fig.5 Amplitude difference under different mass ratio and in⁃erter ratio
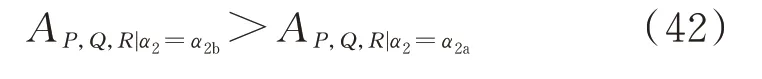
此时从式(42)可以得出α2=α2a的效果较好,故当δ∈(δ1,δ2) 时取α2=α2a及其对应的最优参数——最优频率比式(27)、最优刚度比式(28)和最优阻尼比式(30)。
4 数值验证
为了验证前述解析结果的正确性,使用MAT⁃LAB 进行仿真对比。由上一节可知不同的惯容比会存在不同的最优参数,故分别进行仿真分析。选取激振力的幅值为F0=1000 N,系统参数μ=0.1,当δ=0.1 时,根据前述的解析解计算最优参数,即:υ=1.43,α1=0.189,α2=-0.145,ξ=0.602,此时系统的固有频率比ω'1=1.15,ω'2=3.38,频率比为ω'1/ω1=0.36,ω'2/ω1=1.07;当δ=2 时,根据前述的解析解计算最优参数,即:υ=3.26,α1=6.76,α2=2.79,ξ=5.96,系统的固有频率ω'1=2.6,ω'2=6.62,频率比为ω'1/ω1=0.82,ω'2/ω1=2.09。故图6横坐标频率比选取为0~3,完全涵盖了此范围。利用四阶龙格⁃库塔法,选取计算时间为500 s。略去瞬态响应,取稳态响应的最大值作归一化处理,可以得到给定激励下系统响应的数值解。从图6中,很明显地可以看出无论接地刚度比选取哪一种情况,数值解和解析解都基本一致,验证了前述结果的正确性。
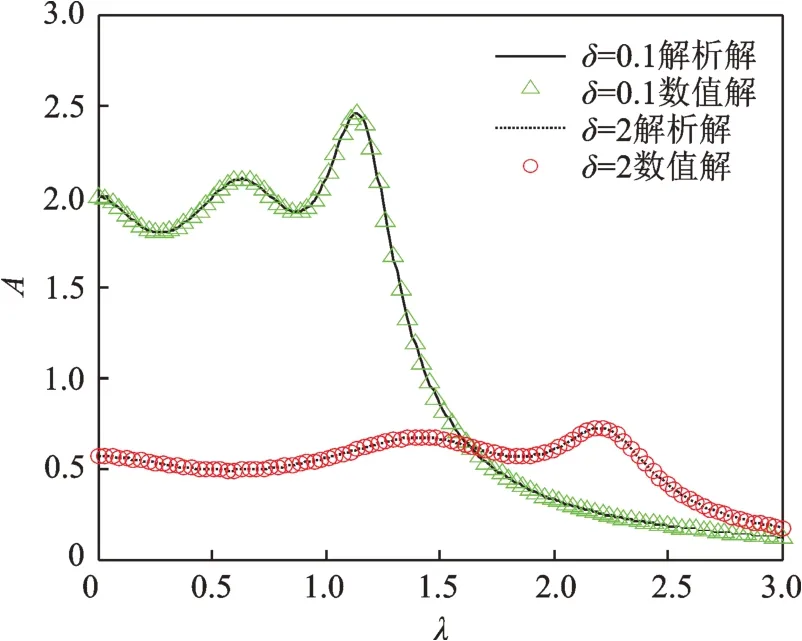
图6 解析解和数值解的对比Fig.6 Comparison between numerical simulation and analyt⁃ical solution
5 最佳工作范围的确定
由3.2 节的分析可知,不同的惯容比范围对应不同的优化参数。当惯容比δ∈(δ1,δ2)时,取质量比μ=0.1,惯容比的有效工作范围为(1,3.909)。在此范围内,图7给出了惯容比对幅频曲线的影响。由图7可知,惯容比δ越大,主系统振幅越小,且有效的减振频带越宽,减振效果越好。
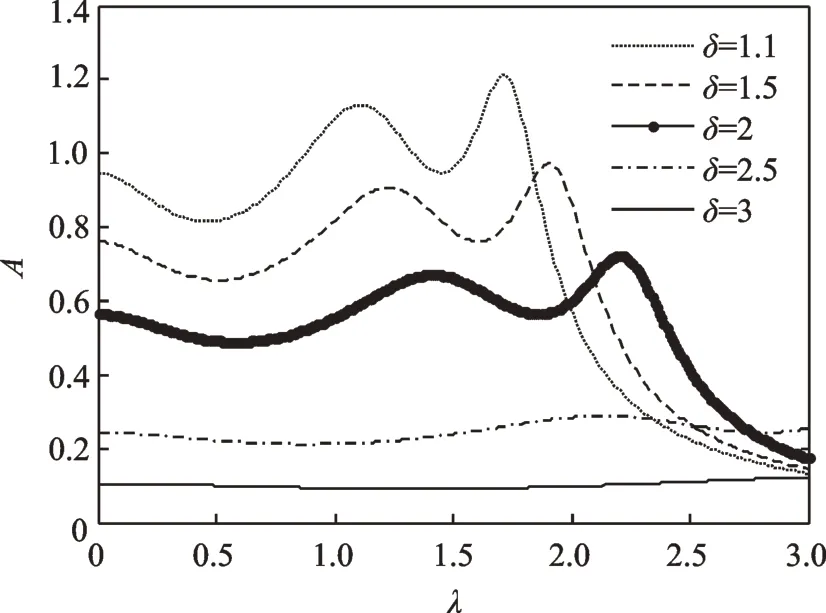
图7 惯容比对幅频曲线的影响Fig.7 Influence of inertia ratio on amplitude-frequency curve
当惯容比δ∈(0,δ1]∪[δ2,+∞),取质量比μ=0.1,惯容比的有效工作范围为(0,1]∪[3.9090,+∞)。在此范围内得到图8。由图8可知,惯容比δ越小,主系统振幅越小,直到惯容比减小至零,这个范围的控制效果达到最优。

图8 惯容比对幅频曲线的影响Fig.8 Influence of inertia ratio on amplitude-frequency curve
通过对比图7和图8可明显地观察出,图8中的优化结果不如图7中的优化结果。考虑实际工程的可行性,当惯容比δ∈(0,δ1]∪[δ2,+∞),在动力吸振器中加入惯容将增加整个系统的质量却没有发挥它良好的控制性能,应该避免这种情况的出现。故在常规参数下,δ∈(δ1,δ2)为本文模型的最佳工作范围。在实际的应用中可采取折中的方法选取最优参数,当惯容比取值小于或等于最佳范围下限时,可选取惯容比略大于下限时所对应的最优参数,例如μ=0.1,δ=0.7,0.8,0.9,1 时,均取略大于最佳范围下限的值δ=1.01,对应的最优参数为υ=0.23,α1=2.03,α2=1.21,ξ=33.44。此时取激励幅值F0=1000 N,利用MATLAB 进行仿真,可得到图9。从图9可以看出,这样设计吸振器仍有较好的减振效果。但当惯容比的取值接近该范围的上限时,例如δ=3.9,对应的最优参数为υ=91.47,α1=3198,α2=922.48,ξ=6.33。显然,此时的刚度比过大,在实际的工程中较难实现,故应该避免选择过大的惯容比。
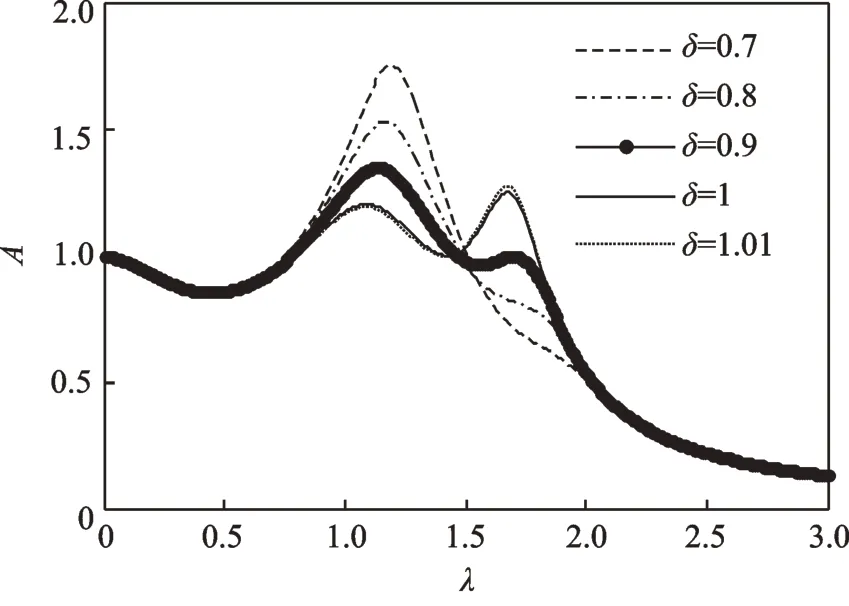
图9 接近最佳工作范围下限的惯容比对幅频曲线的影响Fig.9 Influence of inerter ratio close to the lower limit of op⁃timal working range on amplitude frequency curve
6 模型对比
6.1 简谐激励下响应对比
为了验证本文提出的动力吸振器模型的减振效果,取μ=0.1,将本文提出的模型与其他3 种模型(即文献[3],[9],[14]的模型)进行对比,得到的幅频曲线如图10 所示,其中3 种模型的最优参数选取如表1所示。从图10 中可以看出,本文提出的模型中惯容比取最佳工作范围时减振效果明显优于其他几种情况,且拓宽了频带范围,为以后的研究提供了良好的依据。
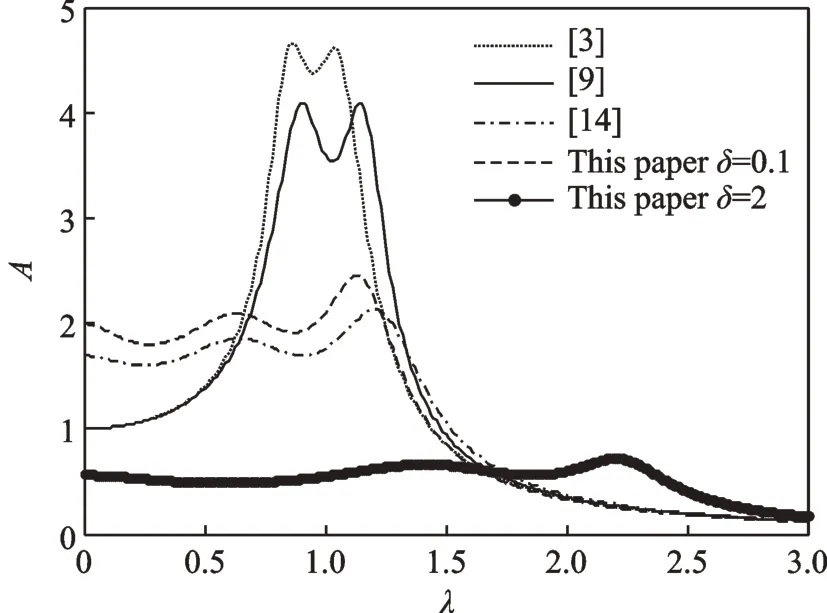
图10 μ=0.1 时与其他形式动力吸振器模型的对比Fig.10 Comparison between the DVA in this paper and oth⁃er DVAs under μ =0.1
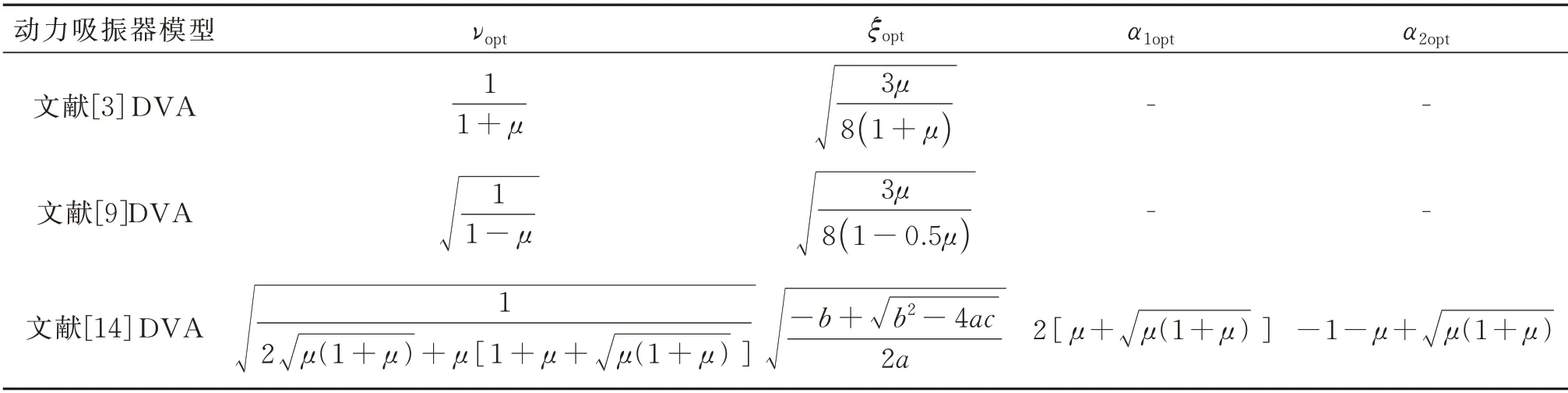
表1 吸振器模型参数最优设计公式Tab.1 Optimal design formula for model parameters of DVAs
6.2 随机激励下响应对比
由于实际工程中机械或结构受到的激励多为随机的,故本文近一步地讨论吸振器在随机激励下的减振效果。设该系统受均值为零、功率谱密度为S(w)=S0的白噪声激励,则本文模型与其他3 种吸振器模型绝对位移响应的功率谱密度函数分别为:
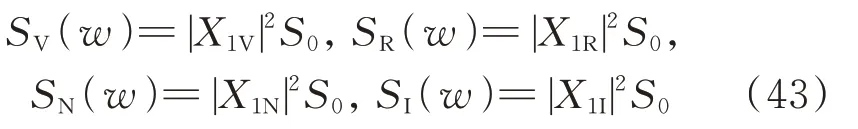
式中 下角标V,R,N,I 分别代表文献[3]中的Voigt 模型,文献[9]提出的接地式动力吸振器模型,文献[14]提出的N⁃三要素模型以及本文模型。其他模型与本文模型主系统的位移均方值为:
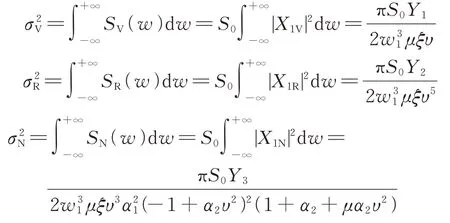

其中:
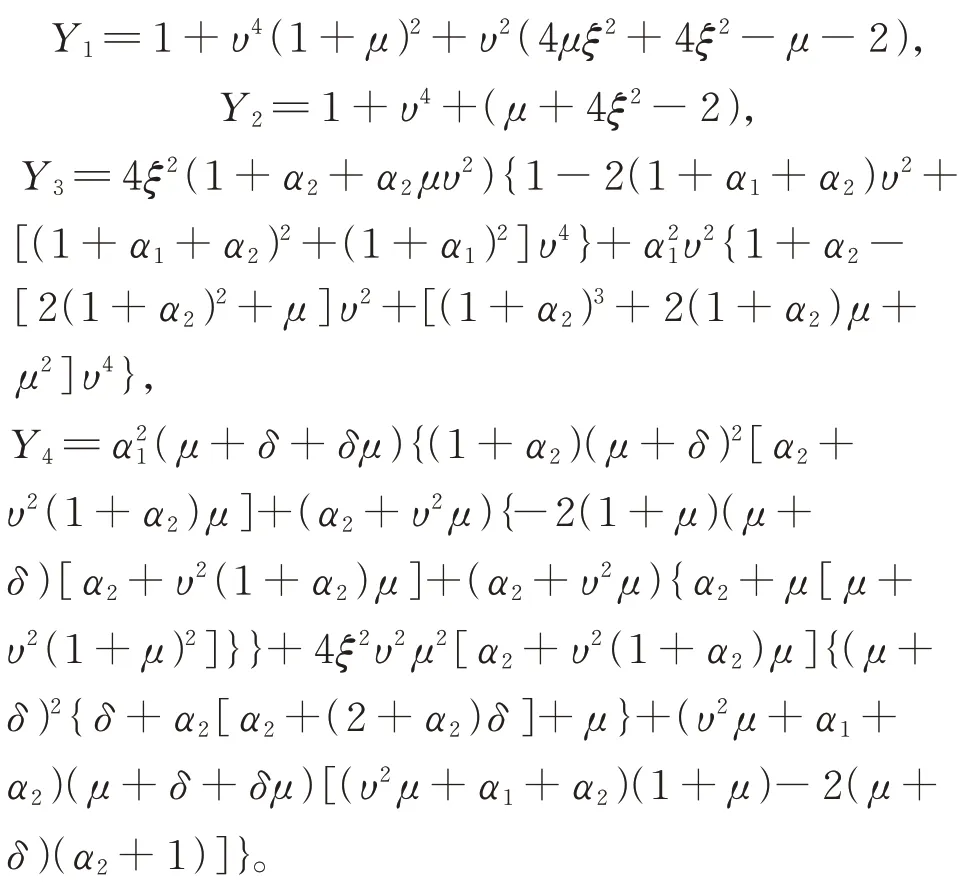
选取4 种动力吸振器的质量比为μ=0.1,根据现有文献中的结果和本文计算的最优结果,可以得到4 种吸振器的均方值分别如下:
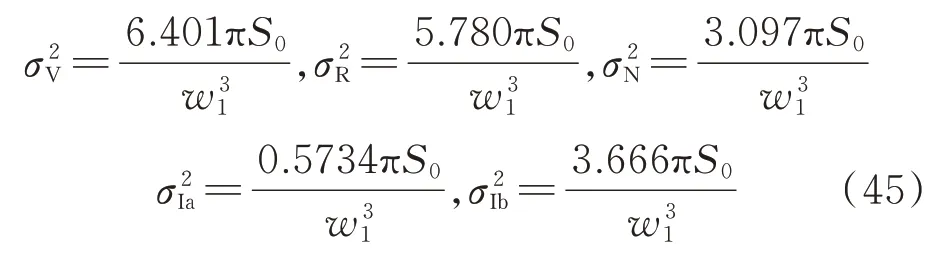
从上面的结果中可以发现,当主系统的参数相同时,本文模型惯容比取最佳工作范围时具有良好的减振效果。
为了更贴近实际工程,本文构建了50 s 均值为0方差为1 的随机力激励,其时间历程如图11 所示。选取系统参数为m1=1 kg,主系统刚度为k1=100 N/m,吸振器质量为m2=0.1 kg,根据文献[3,9,14]和本文的推导过程得到其他最优参数。主系统不附加动力吸振器的位移响应如图12 所示。图13~17 为主系统附加4 种不同的动力吸振器的位移响应。表2为主系统位移方差统计值及其衰减比。从图13~17和表2可以发现,在本文模型中,当惯容比为最佳工作范围时比其他3种模型具有更优良的吸振性能。
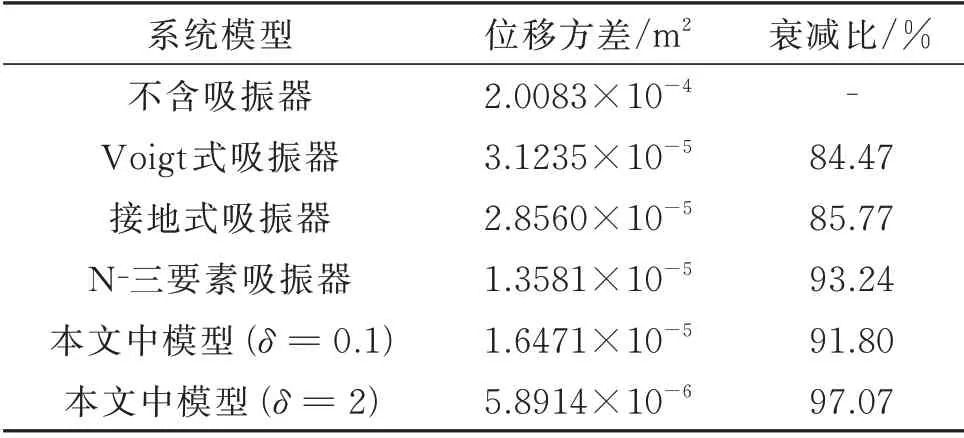
表2 主系统位移方差统计值及其衰减比Tab.2 The variances and reduction ratios of the primary system
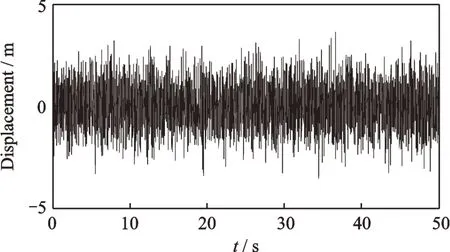
图11 随机激励时间历程Fig.11 The time history of the random excitation

图12 无吸振器的主系统时间历程Fig.12 The time history of the primary system without DVA

图13 附加Voigt 型动力吸振器的主系统时间历程Fig.13 The time history of the primary system with Voigt DVA
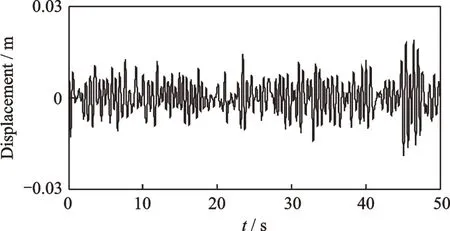
图14 附加接地式动力吸振器的主系统时间历程Fig.14 The time history of the primary system with ground⁃ed DVA

图15 附加N-三要素型动力吸振器的主系统时间历程Fig.15 The time history of the primary system with N-three elements DVA

图16 附加惯容和接地刚度动力吸振器的主系统时间历程(δ = 0.1)Fig.16 The time history of the primary system with inerter and grounded stiffness DVA under δ = 0.1
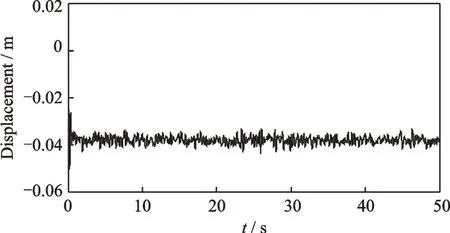
图17 附加惯容和接地刚度动力吸振器的主系统时间历程(δ = 2)Fig.17 The time history of the primary system with inerter and grounded stiffness DVA under δ = 2
7 结 论
本文提出了一种含惯容和接地刚度的黏弹性动力吸振器模型,对其参数进行了研究。通过基于固定点理论的H∞优化得到吸振器的最优频率比、最优刚度比和最优阻尼比。在参数优化过程中,发现惯容比在一定范围内有两组优化参数。考虑实际工程应用,在常规参数下比较两组参数对系统的控制性能的影响,确定了惯容的最佳工作范围。分析惯容在最佳工作范围内外系统参数的选择对系统响应的影响,给出实际工程应用的建议。然后与传统吸振器在简谐激励和随机激励下的对比发现,本文提出的模型中,当惯容比在最佳工作范围时可以大幅度地降低振动幅值,拓宽了振动频率的适用范围。进一步研究表明,在惯容比的最佳工作范围内,惯容比越大,动力吸振器的减振效果更佳。
