基于量子概率理论的出行方式选择模型研究

王钰涵，赵传林，孙淑敏，贺少松

(北京建筑大学 土木与交通工程学院，北京 102616)

随机效用最大化模型已主导出行选择建模数十年，但其不能充分解释行为复杂性，这一不足使人们不断探索新的建模方法。基于效用最大化理论的非集计多项Logit模型因其概念明确、计算方便的特点，逐渐成为目前出行方式选择研究领域中运用最为广泛的方法，但模型要求出行者选择结果的影响因素彼此之间应无相互影响，这在现实条件下难以满足。其他扩展研究成果如后悔最小化理论、决策场理论等选择模型也未撼动随机效用最大化模型的主导地位。

综上分析，量子概率的思想跳出了效用最大化和后悔最小化理论的框架，不是通过在模型中加入效用函数的随机抽样来产生概率输出，而是运用量子理论解决认知、决策过程中的不确定性问题，实现了对个体决策过程随机性的描述。已有研究者通过试验研究证明，人类的决策行为其实就是量子行为，但目前国内并未有将量子概率理论应用到出行方式选择模型问题方面的研究。本文在介绍几何类量子概率模型基础上，结合对模型参数的敏感性分析，讨论出行方式选择问题。

1 量子概率模型

1999年，物理学家通过延迟选择量子擦除试验证明：任何一种基本的量子现象，只有在其被记录之后才是一种现象，在没有完成试验之前，光子的位置和状态无法确定，依然处于叠加态中。据此，在传统出行方式预测模型中，依据人们对交通方式的选择倾向预测最终选择结果是不准确的，因为出行者在未做出决定前，这个倾向便不能被记录，存在不确定性，人类的推理、决策过程并不能完全刻板遵循古典概率理论。因此，引入量子概率理论可合理描述一种不确定的状态，称为叠加态，这就在出行者决策的建模过程中引入了不确定性。同时，在量子概率理论中，系统状态以波函数表示，只要没有观测者，波函数将根据薛定谔方程平滑确定性地演化，一旦发生观测事件，波函数便坍缩成某一观测结果，坍缩本身的结果是随机的，波函数会给每种可能发生的结果分配数值，这种特质为实现个体决策者头脑中决策过程的随机性提供了可能。

1.1 量子概率基本思想

量子概率是在量子力学中引入概率概念，量子概率与古典概率既有联系又有区别。在古典概率框架中，概率值是通过大量实践和总结或推论之后得出的，而在量子概率理论下，人们的信念-行动状态由希尔伯特空间中的向量描述。希尔伯特空间是欧几里得空间的推广，可视为“无限维的欧几里得空间”，其不再局限于有限维的情形，是量子力学的关键性概念和描述量子物理的基本工具之一。

从数学形式来看，量子概率不是直接把古典概率论中的概率改写成复数形式，而是引入了一个新量ψ，称为概率幅，可被认为是古典概率在复数域的扩展，其在描述粒子的量子行为和位置时又被称为波函数，具体形式如式(1)：

ψ=ψ(a,b,c,t)

(1)

式(1)表示，时刻t在点(a,b,c)附近单位体积内发现粒子的概率。

在古典概率论中，随机事件X的可能取值为x1,x2,x3,…,xi，其中i∈N*，相应的概率为p1,p2,p3,…,pi，这些概率可表示X的概率分布。在量子系统中，随机事件X的可能取值为|x1〉,|x2〉,|x3〉,…|xj〉，将概率定义为复数形式ψ1,ψ2,ψ3,…,ψj，其中j∈N*，由于在量子概率体系中，事件对应于希尔伯特空间，因此通常将概率分布写为向量的形式，表示最终结果由多个状态叠加而成：

ψ(x)=ψ1|x1〉+ψ2|x2〉+ψ3|x3〉+…+ψj|xj〉

(2)

或

|X〉=ψ1|x1〉+ψ2|x2〉+ψ3|x3〉+…+ψj|xj〉

(3)

其中一系列随机事件的可能取值|x1〉,|x2〉,|x3〉,…|xj〉可看作是j维空间的基向量，也就是坐标轴，ψ1,ψ2,ψ3,…,ψj可认为是每个维度上的坐标。

2个子空间LA、LB各由1组表示所测量事件可能选项的向量单独定义，即子空间LA由{|x1〉,|x2〉}定义，子空间LB由{|y1〉,|y2〉}定义，由于|x1〉和|x2〉是事件A的不兼容的取值，所以两者可用相互垂直的标准正交向量表示，同理|y1〉和|y2〉也可用相互垂直的标准正交向量表示，φ是2个子空间坐标的夹角，这些标准正交向量组成坐标轴，分别两两构成一个平面，如图1所示。

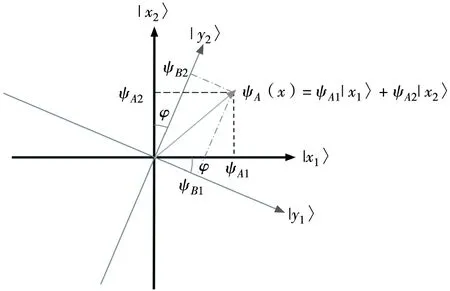
图1 事件在希尔伯特空间的表示Fig.1 Representation of events in Hilbert space

其中对于事件A有2个选项，事件B也有2个选项，信念-状态向量在子空间LA、LB的坐标轴上产生的投影长度分别为ψA1,ψA2,ψB1,ψB2,在不同子空间中可能选项发生的概率值由投影长度与其自身的复共轭的乘积表示，即

(4)

式中：*代表互为共轭。

如果投影结果为实数，则概率表示为平方值：

PA1=|ψA1|2

PA2=|ψA2|2

PB1=|ψB1|2

PB2=|ψB2|2

(5)

在第一个子空间中，信念-状态向量表示为：

ψA(x)=ψA1|x1〉+ψA2|x2〉

(6)

在第二个子空间中，信念-状态向量表示为：

ψB(y)=ψB1|y1〉+ψB2|y2〉

(7)

其中：

(8)

由式(6)～式(8)可以看出，ψA(x)和ψB(y)就是同一个向量在不同坐标中的不同表示方法。由上述过程可知，事件A与事件B具有某种联系，因此A的概率分布与B的概率分布会相互影响，最终的选择结果是由A和B共同作用的。

1.2 几何类量子模型

1.2.1 通用模型

在希尔伯特空间中研究量子概率问题时，可根据情景需要推广出无限个多维子空间。每个子空间由1组表示每个测量事件选项的标准正交向量单独定义，这些标准正交向量形成子空间的一组基，可将其理解为代表不同选项的坐标轴。信念-状态向量在坐标轴上的投影代表了选择每一个选项的潜在动机，其长度的平方就是该选项对应的概率值，因此，概率值可通过几何形式被直接观测。在有n个m维子空间的希尔伯特空间的几何类量子通用模型如式(9)：

(9)

式中：i=1,2,3…,m；Pi代表一个子空间中每个可能选项发生的概率值。

(10)

式中：P(ζ)为某个决策选项发生的最终概率值。

值得注意的是，因为子空间的维度代表了所研究的每个问题可能存在的选项，故每个子空间的维度可以是不相同的。为了便于研究，假设每个问题可能存在的选项数量相同，即子空间维度都为m；对于问题可选选项数量不等的情况，即子空间维度数不相同，今后会进一步展开讨论。

1.2.2 汽车-火车选择模型

基于量子概率，几何类量子模型连续二值选择如图2所示。由于包含汽车和火车2个选项，故模型可以由子空间为二维的希尔伯特空间描述。

图2 连续二值选择的示意Fig.2 Schematic representation of two consecutive binary choices

如图2所示，决策者选择汽车还是火车具有初始信念状态。在这个测量事件中，所有可能的状态都是由基向量|xcar〉，|xtrain〉表示，即初始信念状态可表示为：

|Z〉=ψC1|xcar〉+ψT1|xtrain〉

(11)

式中：ψC1和ψT1分别表示初始信念状态向量在2个坐标轴上的投影长度，是正常数；|xcar〉和|xtrain〉分别表示选择汽车和火车2个向量。可想象1个既不是选汽车也不是选火车的状态，在叠加原理作用下作出决策，决策者状态的向量越接近某个基向量，信念状态向量在坐标轴上的投影长度便越长，得到振幅模的平方越大，该方案被选择的可能性也就越大。

若决策者先被询问一个预备问题(如，问是否倾向于选择环保型出行方式，或问是否倾向于选择更自由的出行方式等)，在新问题的视角下，初始信念状态虽不会改变，但向量参照系发生了变化，即在预备问题Y中选择备选项的概率与在初始问题X中选择的概率不同。新的问题Y由一组基向量|y1〉，|y2〉表示，若决策者做出问题Y中的y1选择，则其信念状态穿过希尔伯特空间，投射到向量|y1〉，此时|y1〉成为新的状态向量，这会在基向量|xcar〉，|xtrain〉上投射出与初始信念状态不同的振幅。由于量子系统的状态空间是线性空间，可以让任意2个状态叠加得到新的状态，故根据通用模型可以写出最终选择火车的概率：

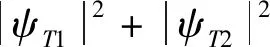
(12)

选择小汽车的概率：

(13)

并且：

(14)

相较于初始信念状态下2种方式的选择概率，受到新问题影响干扰后，选择火车或小汽车的概率也随之改变。也就是说，量子概率模型可解释不同问题顺序、干扰项和情境效应等的试验结果，展示了随机效用理论不具备的优点。

2 敏感性分析

本文假设在合适的中长途出行中，火车与汽车的成本差距不大，故而不考虑出行成本问题。为验证不同初始信念状态下预备问题对火车和小汽车选择概率的影响，对模型进行敏感性分析，不同情景模拟取值情况见表1。

表1 不同情景模拟取值情况Table 1 Values of different scenarios simulation

表1中，预备问题即在决策者做出“汽车或者火车”选择之前会被问及的问题；初始信念状态为决策者没有受到预备问题干扰时的对“汽车”和“火车”的初始选择偏好；※代表决策者支持此选项；φ表示初始坐标系与预备问题坐标系的夹角角度，从理论上讲，在“环保型或者不环保型”预备问题中，因决策者支持环保选项，环保型坐标轴应更靠近“Train”选项，故φ可取范围为0°～45°；在“高自由度或者低自由度”预备问题中，因决策者支持高自由度选项，高自由度坐标轴应更靠近“Car”选项，故φ可取范围为45°～90°，为使模拟数据效果明显，选取φ值分别为20°和60°。α为初始信念状态向量与初始坐标系横坐标的夹角角度，理论上可以为0°～90°中的任意值，为使模拟数据效果明显，避免预备问题无效修正，此处设置α取值为15°、30°、45°、60°、75°。

将上述情景用几何类量子模型进行连续二值选择，当预备问题为{环保型，不环保型}，以α取15°和75°为例，得到的结果如图3所示。

当预备问题为{高自由度，低自由度}，以α取15°和75°为例，得到的结果如图4所示。

分析表2～表4，可以发现：

表2 环境预备问题下概率计算结果Table 2 Probability calculation results under the environment preparation problems

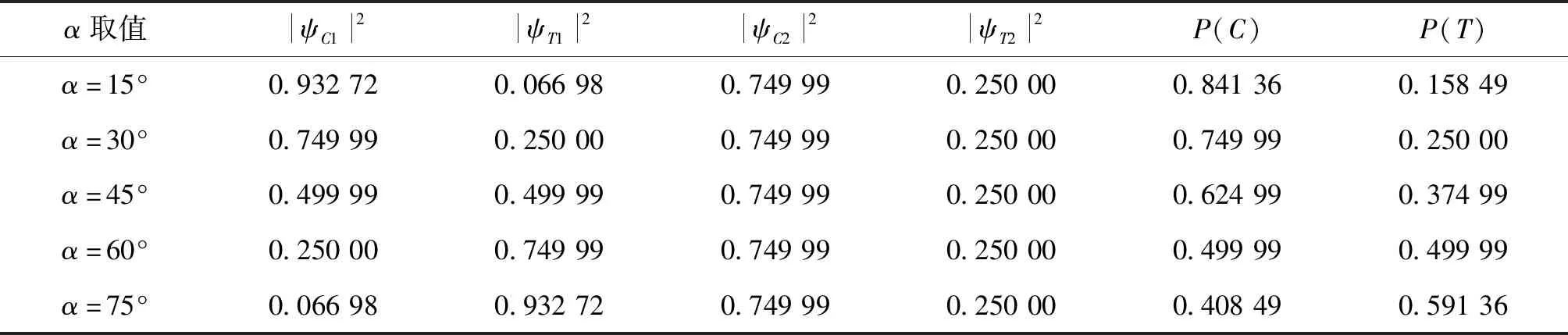
表3 自由度预备问题下概率计算结果Table 3 Probability calculation results under the degree of freedom preparation problem

表4 预备问题干扰下选择结果对比Table 4 Comparison of selection results under the interference of preparatory questions

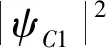
(a) φ=20°，α=15°

(a) φ=60°，α=15°

2) 对火车的初始选择概率随着α的增大而增大，对小汽车的初始选择概率随着α的增大而减小，即信念向量越靠近某个选择，其在基向量上的投影越长，该方案被选中的可能性就越大，如随着α增大，向量逐渐远离“Car”选项，小汽车的选择概率减小，火车的选择概率上升。

3) 由表2可以看出，如果决策者倾向环保出行，α取15°、30°、45°、60°时，对小汽车的选择意念皆有所减弱，对火车的选择意念有所增强，即P(C)<|ψC1|2、P(T)>|ψT1|2，而α取75°时则有所不同，即P(C)>|ψC1|2、P(T)<|ψT1|2；同理，由表3可以看出，如果决策者倾向高自由度出行方式，α取45°、60°、75°时，对小汽车的选择意念皆有所增强，对火车的选择意念有所减弱，即P(C)>|ψC1|2、P(T)<|ψT1|2，而α取15°时则不同，即P(C)<|ψC1|2、P(T)>|ψT1|2，进一步验证了决策者最终决策结果受2个子空间综合影响。

4) 由表3可以看出，当α+ψ=90°时(表中α取30°)，初始信念状态与预备问题存在相同的概率倾向，此时预备问题不具有更新和修正效果。

5) 虽倾向环保出行的决策者对于小汽车的选择概率均减小，但当初始信念对小汽车具有严重偏好时(如α取15°，决策者对小汽车的选择意愿强烈)，会导致P(C)>P(T)；同理，虽倾向高自由度出行的决策者对于小汽车的选择概率均增加，但当初始信念对火车具有严重偏好时(如α取75°，决策者对火车的选择意愿强烈)，会导致P(C)

6) 由表4选择结果对比可知，环境预备问题下α取30°和45°时，初始选择状态被改变，由(汽车，相等)转为(火车，火车)；自由度预备问题下α取30°和45°时，初始选择状态被改变，由(相等，火车)转为(汽车，相等)，但由于α取45°时选择汽车和火车的概率相等，故认为决策者仍有可能坚持初始选择状态，这种差异是由不同预备问题对选项的干扰效果不同造成的，由此可见，决策者对预备问题某一选项的倾向越强烈，即预备问题基向量越靠近某一坐标轴，概率修正效果越明显。

基于几何类量子模型，环保倾向的预备问题会提高火车选择概率，高自由度预备问题会提高小汽车选择概率，交通管理者可以通过信息干扰、情感引导等强化人们对出行方式选择倾向，对初始信念状态进行修正，这为实现出行者在不同交通出行方式的合理分配提供了新的思路。

3 结论

1) 不同于随机效用理论框架，量子概率作为物理学的前沿理论，为行为决策建模提供了新的研究方向。

2) 本文介绍了一种出行方式选择的几何类量子概率模型，对火车和汽车2种出行方式选择情形进行敏感性分析，考虑不同初始信念状态，并结合不同预备问题实现了将初始信念状态到最终信念状态的转化。研究结果表明，量子概率理论弥补了效用理论在解释问题干扰、顺序影响、情境效应等的不足，进一步验证了量子概率理论在交通决策建模领域的应用可行性。

3) 下一步将设计并开展量子概率的试验研究，结合试验结果进一步分析量子决策行为。此外，基于薛定谔方程考虑量子模型的动态属性、结合交通出行的拥挤效应建立量子均衡模型、对比量子理论和效用理论的效果，也是未来的研究方向。