基于压电分流技术的PT 对称梁散射特性研究

王刚，罗彩明，张晓东

（湖南大学汽车车身先进设计制造国家重点实验室，湖南长沙 410082）

宇称-时间（Parity-Time，PT）对称由Bender 和Boettcher 于1998 年提出［1］，他们发现在满足PT 对称的条件下，系统的哈密顿量即使是非厄米的也可以具有实数的本征值.系统具有PT 对称性的条件是势函数共轭对称，即势函数的实部偶对称、虚部奇对称.PT 对称系统的一个重要性质为PT 对称性的自发性破缺，具体表现是：当势函数虚部在某一阈值以下时，哈密顿量的本征值全部为实数，系统处于PT对称相；当势函数虚部越过该阈值时，哈密顿量的本征值开始有复数产生，此时对应于PT 破缺相.这一阈值也被称为相变点或奇异点（Exceptional Point）.PT 对称将量子力学拓展到了非厄米范围，此后它便成了量子力学中的一个重要研究方向.现阶段非厄米PT 对称的研究工作已经拓展到光学和声学领域中，表现出许多奇特的物理现象.在光学领域的研究中，调节折射率的分布，使折射率在传播方向上满足实部偶对称、虚部奇对称，即可构造PT 对称光学系统［2-6］；而在声学领域的研究中，当声学系统满足一定条件时，它也会有PT 对称性，例如Fleury 等人［7］通过调节两个麦克风连接的阻抗使得麦克风的等效质量密度共轭对称，从而利用PT 对称性实现了一种声学隐身传感器.

PT 对称性的关键点在于引入均衡的增益和损耗，而目前，固体介质中针对弯曲波的PT 对称性的研究相对较少，其中一个重要的原因是自然介质难以实现能量损耗和能量增益之间的平衡.压电材料由于能够实现机械能与电能之间的转化，并且具有易于调控的特点，有望解决这一问题.Christensen 等人［4］利用压电半导体中的声电效应构造了声子PT对称系统，并分析了其中的单向无反射现象.Hou 等人［8］基于压电分流单元，提出了一种可调PT 对称系统，通过改变分流电路的阻抗便可以调节PT 对称系统奇异点出现的频率.上述研究工作所提出的PT 对称系统均是针对纵波而言的，所获得的研究成果为PT 对称系统的应用奠定了理论基础.而与纵波相比，弯曲波的理论模型更为复杂，因此针对弯曲波的PT对称系统同样值得研究.

本文首先基于欧拉梁的假设，推导了针对弯曲波的PT 对称条件；然后基于该条件，利用压电分流单元设计一种PT 对称梁，并采用等效介质法和有限元仿真，得到增益单元、损耗单元的等效质量密度和等效弯曲刚度；最后通过传递矩阵法和有限元仿真证明了PT 对称梁中的单向无反射现象，并通过计算散射矩阵的特征值和特征向量说明了单向无反射现象源于奇异点的存在.本文所提出的PT 对称梁对于弯曲波有许多潜在的应用，包括增强传感、弯曲波放大和非对称控制等.

1 PT 对称梁的设计与分析

1.1 弯曲波PT 对称条件

根据欧拉梁假设，弯曲波沿x轴传播时满足控制方程［9］：

式中：w(x)、Deff(x)、ρeff(x)和hb分别表示梁的横向位移、等效弯曲刚度、等效质量密度和厚度.若梁满足PT对称性，则根据式（1）可以得到：

公式（3）和公式（4）表明，若满足PT 对称性，则要求等效质量密度ρeff(x)和等效弯曲刚度Deff(x)关于原点共轭对称.

1.2 PT 对称梁设计

压电分流单元已经被证明可以有效地改变基体材料的等效弯曲刚度而几乎不改变其等效质量密度［10］，因此，可以通过设计合理的压电分流单元使其满足公式（3）和（4）所提出的等效质量密度和等效弯曲刚度共轭对称条件.图1（a）为所设计的PT对称梁示意图，基体梁上表面贴有两块压电片，两块压电片分别连接由正、负电阻与电感并联组成的分流电路，从而与基体梁部分构成损耗单元、增益单元.分流电路中，正、负电阻的作用分别是衰减和放大弯曲波.正电阻Rsh和电感Lsh并联后的分流阻抗ZL、负电阻-Rsh与电感Lsh并联后的分流阻抗ZG分别为：

式中：ω为角频率.

PT 对称梁中的负电阻可以通过图1（b）所示的Non-Foster电路来实现［11-12］，大电感可以用图1（c）所示的Antoniou’s 模拟电感电路实现［13-14］.此外，分流电路中的电感会与压电片的固有电容产生谐振，从而使得增益单元、损耗单元的等效弯曲刚度Deff(x)与弯曲波频率相关，该现象在第2节进一步说明.

图1 PT对称梁示意图、Non-Foster电路及Antoniou’s模拟电感电路Fig.1 Schematic illustrations of PT symmetric beam，the Non-Foster circuit and the Antoniou’s circuit

1.3 PT对称梁的特性分析

本节基于等效介质理论计算增益单元、损耗单元的等效参数，并通过传递矩阵法，针对图1（a）所示PT 对称梁，计算弯曲波分别从左端和右端两种入射情况下的透射系数和反射系数.同时，使用有限元软件COMSOL Multiphysics 进行有限元仿真，以验证理论计算结果的准确性.

如图2 所示，令基体梁的厚度及弹性模量分别为hb、Eb，压电片的厚度和长度分别为hp、Lp.假设压电片除了垂直于x轴的端面外，其余表面均为自由状态，且压电片仅在z轴存在极化，因此压电片的本构方程可简化为［15-16］：

图2 等效参数求解原理示意图Fig.2 Configurations to calculate the effective parameters

式中：T1和S1分别为压电片x轴方向的应力和应变；D3和E3分别为压电片的电位移和电场强度d31分别对应于压电片柔度系数、恒应力介电常数、压电应力常数.

另外，图2 所示单元内任意一点x方向的位移u(x，z) 为纵波位移u0(x) 与弯曲波位移wp(x) 的组合：

由于压电片的厚度与基体梁的厚度处于同一个数量级，因此电场强度E3在z方向不能被认为是恒定的.本文采用文献［17］提出的假设，认为电场强度E3在z方向呈线性分布，即电场强度E3和电势V(x，z)可以用如下公式表述：

电位移D3满足控制方程［18］：

联立公式（6）～公式（10），便可以求出系数a(x)、b(x)、c(x)和压电片上表面的电压Vup［17］：

以基体梁的中性面为基准面，对应力求积分，可以得到单元x-y截面上的弯矩M、法向力N和剪切力T：

其中系数I、J、K、F和G通过下式计算：

基于公式（15）～公式（17），图2所示单元的运动控制方程为：

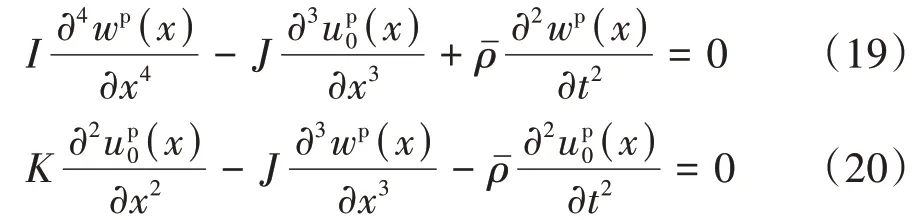
令γn表示特征方程（21）的特征根，则纵波和弯曲波wp(x)的表达式分别为：

对于没有贴压电片的基体梁，纵波wb(x)和弯曲波解耦，运动控制方程分别为［19］：

对于基体梁中未贴压电片的部分及贴有压电片的部分，本文分别定义向量Yb和Yp：

根据公式（22）～公式（28），公式（15）～公式（17）可以用以下矩阵形式表述：

其中：

根据连续性条件，结合公式（31）和公式（32），可以得到增益单元或损耗单元的传递矩阵Mi，其中i=G表示增益单元，i=L表示损耗单元：

式中：Pp为对角矩阵.

1.3.1 等效参数

本文仅对波长远大于单元长度Lp的低频弯曲波进行分析，采用等效介质理论计算结构的等效参数［20］.因为增益单元和损耗单元的等效参数求解原理相同，对应的等效参数计算过程相同，所以本文仅以损耗单元为例介绍等效参数求解过程.

令x=0，根据公式（36），Yb(Lp)与Yb(0)之间满足：

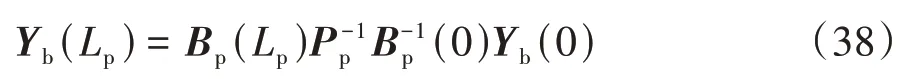
求解等效质量密度ρeff时，需要获取单元的质量，这要求单元任意一点的横向加速度均相同.如图2（a）所示，损耗单元整体相对于虚线方框所示的原始位置作幅值为A1的横向简谐振动，并且限制其左、右边界的纵向位移和旋转角度为0.依据上述边界条件，基于公式（38）可求解向量中Yb(0)、Yb(Lp)的未知元素，从而得到损耗单元的等效质量密度ρeff：

如图2（b）所示，求解等效弯曲刚度Deff时，在单元左、右两侧相对于虚线方框所示的原始位置分别施加大小为-α1、α1的转角，令wp(0)=wp(Lp)=0.弯曲波和纵波相互耦合，若限制单元两端纵向位移为零，则需要确定增益单元、损耗单元的中性面.但是该中性面对于本文中的增益单元、损耗单元来说很难确定，因此，本文只限制单元左边界的纵向位移(0)=0，而令右边界的纵向力为零.依据上述边界条件便可以基于公式（38）求解向量中Yb(0)、Yb(Lp)的未知元素，从而得到等效弯曲刚度Deff：

为了验证等效介质法计算结果的正确性，本文针对损耗单元和增益单元，使用COMSOL 分别建立了如图2所示2种情况下的二维有限元模型.有限元模型中，认为单元满足平面引力假设，施加的边界条件与等效介质法中的边界条件一致.

求解等效质量密度ρeff时，分别在左、右边界上，对单元所受的z方向力求线积分即可得到对应边界上的剪切力T(0)、T(Lp)；而求解等效弯曲刚度Deff时，在右边界上对单元所受的y方向力矩求线积分可得到力矩M(Lp).得到剪切力和力矩之后，便可以通过公式（39）和公式（40）分别计算得到单元的等效质量密度ρeff及等效弯曲刚度Deff.

等效参数法和有限元仿真中，损耗单元和增益单元的几何参数及材料参数如表1 所示.另外，电感与压电片的固有电容会产生谐振，因此取谐振频率f0=500 Hz，分流电阻Rsh=1 000 Ω.等效参数法和有限元仿真的计算结果在2.1节进行讨论.

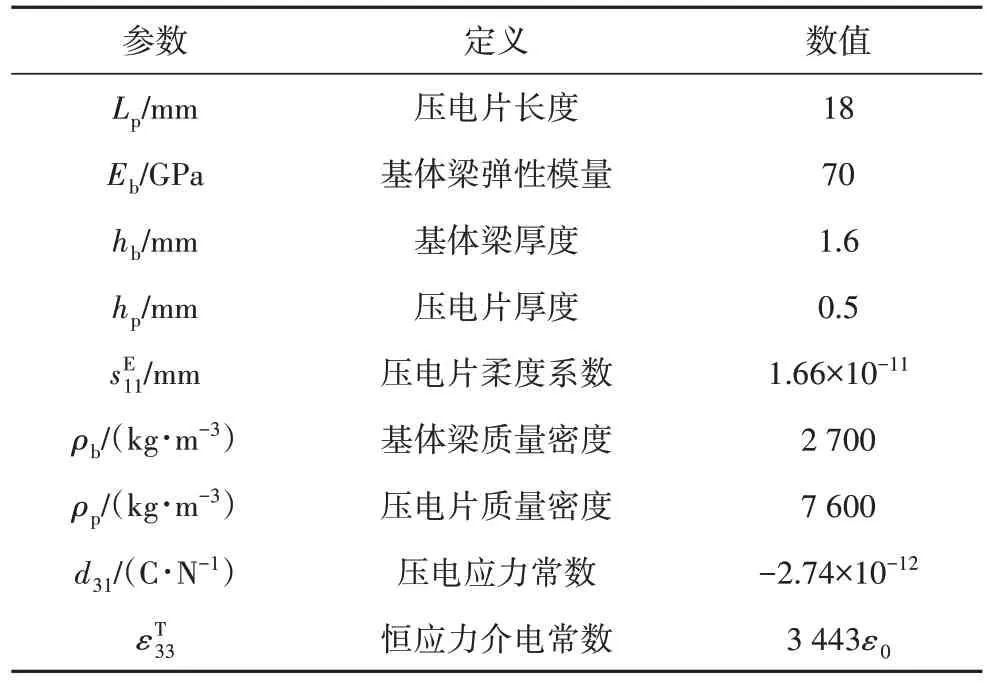
表1 损耗单元和增益单元的几何参数及材料参数Tab.1 Geometrical and material parameters of loss and gain units

1.3.2 透射系数及反射系数

为了表述方便，本文用下标l表示弯曲波从左端入射，用下标r 表示弯曲波从右端入射，将弯曲波从左端入射时的透射系数和反射系数分别定义为左透射系数tl和左反射系数rl.同理，定义弯曲波从右端入射时的右透射系数tr和右反射系数rr.

在PT 对称梁的左端或右端施加一个单位位移，即

式中：L表示两块压电片之间的距离.求解公式（41）便可以分别得到左透射系数tl、左反射系数rl、右反射系数rr、右透射系数tr，进而可以得到弯曲波的散射矩阵S［21］：

为验证传递矩阵法计算结果的正确性，本文使用COMSOL 软件建立如图3 所示的有限元仿真模型，基体梁上含有增益单元、损耗单元.分别在左端激励点和右端激励点施加力载荷，产生弯曲波.为了抑制边界反射，基体梁的两端各连接一个完美匹配层，其他边界保持自由状态.完美匹配层的长度至少为研究波长的1∕2［22］，在本文中，波长的最大值约为0.384 4 m，则本文中完美匹配层的长度设为0.2 m.由于激励点关于原点O对称，所以观测点相对原点也要对称分布.为了避免受到激励点的影响，观测点与激励点之间要保持一定距离.观测点A和观测点B的坐标分别为（-0.35 m，0）和（0.35 m，0），左端激励点和右端激励点的坐标分别为（-0.5 m，8.0×10-4m）和（0.5 m，8.0×10-4m）.图4 为试验装置图，在图4 中，梁的两端附着有蓝丁胶，用来减少反射.信号发生器产生的信号经过功率放大器后作用在压电激励器上，产生弯曲激励.激光测振仪用来测量指定点的位移响应，它与信号调理器、数据采集卡、电脑共同组成信号采集处理系统.试验中所需要的负电阻和电感可以分别通过图1（b）和图1（c）所示电路来实现.

图3 有限元仿真示意图Fig.3 Configuration for finite elements simulation

图4 试验装置图Fig.4 Diagram of experimental setup

传递矩阵法和有限元仿真中，压电片长度Lp=45 mm，两块压电片之间的距离L=300 mm，分流电阻Rsh=1 900 Ω，分流电路的谐振频率f0=500 Hz，其他参数与表1 中所列参数相同.有限元仿真模型的长度为2 005 mm.

2 结果和讨论

2.1 等效参数

基于上述等效介质法和有限元仿真，计算得到增益单元和损耗单元的等效质量密度ρeff和等效弯曲刚度Deff.为了表达方便，本文采用归一化等效质量密度ρeff∕ρb和归一化等效弯曲刚度Deff∕Db来表征增益单元、损耗单元的等效参数.等效介质法和有限元仿真计算得到的归一化等效参数分别如图5 和图6 所示.由图5（a）可知，通过2 种方法得到的增益单元和损耗单元的归一化等效质量密度实部Re(ρeff∕ρb)在计算频率范围内几乎保持不变，并且与分流阻抗无关.由图5（b）可知，归一化等效质量密度虚部Im(ρeff∕ρb)数值很小，可以认为，等效质量密度ρeff在计算的频率范围内为实数.由图6（a）和图6（b）可以发现，增益单元和损耗单元的等效弯曲刚度Deff共轭.因此，本文提出的PT 对称梁满足公式（3）和公式（4）所提出的等效质量密度ρeff和等效弯曲刚度Deff共轭对称条件.由于电感和分流电阻Rsh的存在，增益单元和损耗单元的等效弯曲刚度Deff与弯曲波频率相关.等效介质法和有限元仿真获取的结果总体上相吻合，存在部分差异的原因主要在于等效介质法存在的局限性，如压电片z方向上电场线性分布的假设等.

图5 归一化等效质量密度Fig.5 The normalized effective mass density

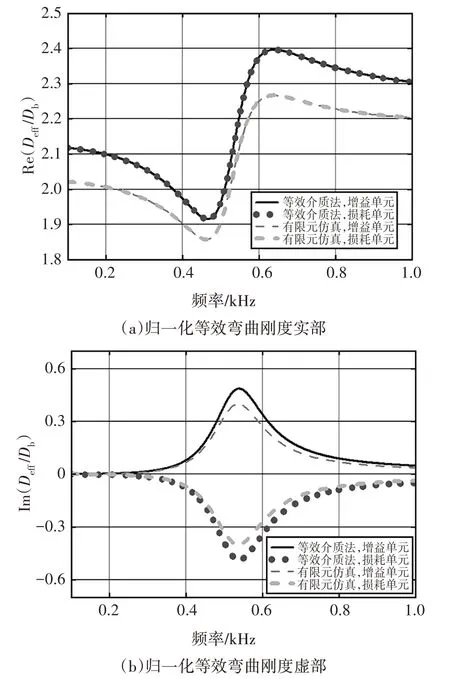
图6 归一化等效弯曲刚度Fig.6 The normalized effective bending stiffness

为了进一步表征归一化等效弯曲刚度Deff∕Db与分流电阻Rsh、弯曲波频率的关系，本文采用等效介质法计算不同分流电阻Rsh及不同频率的弯曲波激励下损耗单元的归一化等效弯曲刚度Deff∕Db，计算结果分别如图7 和图8 所示.由图7 可知，当弯曲波的频率远离530 Hz时，分流电阻Rsh的取值不会影响归一化等效弯曲刚度实部Re(Deff∕Db) 和虚部Im(Deff∕Db)，并且虚部Im(Deff∕Db)接近0，表明此时损耗单元几乎没有消耗弯曲波能量；当弯曲波频率为530 Hz 附近时，归一化等效弯曲刚度实部Re(Deff∕Db)出现极值，并且增大分流电阻Rsh会使得归一化等效弯曲刚度虚部Im(Deff∕Db)数值减小，从而加强损耗作用.当分流电路的谐振频率f0=800 Hz 时，可以发现图8（a）和图8（b）所示结果分别与图7（a）和图7（b）所示结果相近，只是归一化等效弯曲刚度Deff∕Db的梯度变大，并且随着分流电路谐振频率f0的改变，极值出现的频率变为850 Hz附近.

图7 谐振频率f0=500 Hz时损耗单元归一化等效弯曲刚度与分流电阻Rsh、弯曲波频率的关系Fig.7 The normalized effective bending stiffness of loss element in relationship to shunting resistance and flexural wave frequency when resonant frequency f0=500 Hz

图8 谐振频率f0=800 Hz时损耗单元归一化等效弯曲刚度与分流电阻Rsh、弯曲波频率的关系Fig.8 The normalized effective bending stiffness of loss element in relationship to shunting resistance and flexural wave frequency when resonant frequency f0=800 Hz

由图5～图8 可知，本文提出的PT 对称梁满足公式（3）和公式（4）所提出的等效质量密度ρeff和等效弯曲刚度Deff共轭对称条件.通过改变分流电阻Rsh和谐振频率f0，增益单元、损耗单元的弯曲刚度Deff会产生较大变化.因此，本文所提出的PT 对称梁具有易于调控的特点.

2.2 透射系数、反射系数及散射矩阵

基于传递矩阵法和有限元仿真得到的透射系数和反射系数分别如图9 和图10 所示.图9 表示弯曲波分别从左端和右端入射的情况下透射系数的幅值，由图9 可知，2 种方法得到的透射系数幅值一致，这是因为PT 对称梁具有互易性，即左透射系数与右透射系数相等.在图9 中的阴影部分内，透射系数的幅值大于1，这是由于PT 对称梁是非保守系统，与外界存在能量交换.图10（a）和图10（b）分别表示左反射系数幅值和右反射系数幅值.由图10 可以发现，PT 对称梁对弯曲波的非对称散射特性，即当弯曲波分别从左、右两端入射时，2 种情况下的反射系数幅值不相等，2 种情况下的反射系数都存在零点，该零点对应的弯曲波频率即为单向无反射点，如图10（a）中的520.5 Hz 及图10（b）中的511 Hz.由图9 可以发现，在单向无反射点511 Hz 和520.5 Hz，透射系数的幅值接近1.

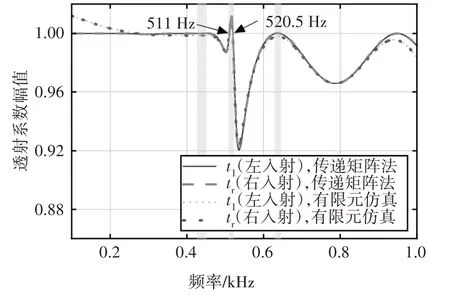
图9 透射系数幅值图Fig.9 The amplitude of transmission coefficients

图10 反射系数幅值图Fig.10 The amplitude of reflection coefficients

根据PT对称性，左反射系数rl、右反射系数rr、透射系数t之间满足：

根据公式（44），可以得到广义守恒定律［23］：

式中：T=|t|2表示透射率；Rl=|rl|2表示弯曲波左端入射时的反射率；Rr=|rr|2表示弯曲波右端入射时的反射率.

由公式（45）可知，当T＜1时，T+=1，表明弯曲波从左、右两端入射时，PT 对称梁中不存在耗散或者放大.当T＞1 时，T-=1，PT 对称梁对弯曲波进行放大.在单向无反射点，由于反射系数为0，根据公式（45）可推知T=1，表明此时PT 对称梁对弯曲波完全透射，这与图9所示结果相符.

为了更好地阐述单向无反射特性，本文从有限元仿真的结果中，提取PT 对称梁在2 个单向无反射点511 Hz 和520.5 Hz 下的归一化弯曲波位移场幅值，结果如图11所示.由图11可知，区域Ⅰ和区域Ⅱ能直观地体现PT 对称梁的散射特性，区域Ⅰ代表左端激励点到损耗单元左边界的范围；区域Ⅱ代表增益单元右边界与右端激励点之间的范围.当511 Hz的弯曲波从左端入射时，区域Ⅰ中有明显的干涉条纹，表明区域Ⅰ中入射弯曲波与反射弯曲波形成了驻波，导致区域Ⅰ中各点的弯曲位移幅值明显不一致.当511 Hz 的弯曲波从右端入射时，区域Ⅱ中各点的弯曲位移幅值近似相等，表明区域Ⅱ中只有向右传播的弯曲波而几乎不存在反射弯曲波，并且区域Ⅰ和区域Ⅱ的弯曲位移幅值相近，表明此时PT 对称梁对右端入射的弯曲波完全透射.当520.5 Hz 的弯曲波从左端入射时，区域Ⅰ中几乎无反射弯曲波存在，并且弯曲波几乎完全透射至区域Ⅱ；而从右端入射时，区域Ⅱ中反射弯曲波与入射弯曲波形成了驻波，导致区域Ⅱ中各点之间的弯曲位移幅值有较大差别.

图11 两个单向无反射点下的归一化弯曲位移场幅值Fig.11 The normalized amplitude of flexural wave displacement fields at two unidirectional reflectionless points

通过散射矩阵S也可以表征PT对称梁的散射性质.由公式（43）定义的散射矩阵，可以得到散射矩阵的特征值λ1、λ2和特征向量V1、V2，结果分别如图12和图13 所示.图12 和图13 中的实心圆点代表单向无反射点520.5 Hz，阴影部分表示透射率T＞1 的弯曲波频率范围.将图12（a）与图9所示结果对比可以发现：当T≤1 时，两个特征值的模均为1，散射矩阵的两个特征向量满足，此时对应于PT对称相；而当T＞1 时，其中一个特征值的模大于1，另一个特征值的模小于1，散射矩阵的两个特征向量满足此时对应于PT 破缺相［24］.在单向无反射点520.5 Hz，同时也是PT 对称相与PT 破缺相之间的临界点（相变点，也即奇异点），两个特征值发生简并.由图13 可知，在单向无反射点520.5 Hz，两个特征向量也会发生简并，这说明PT 对称梁的奇异点即为单向无反射点.此外，图10（a）所示的单向无反射点也可以通过特征向量来解释.例如，在520.5 Hz 的奇异点，两个特征向量的第二分量为零，表明从左端入射时反射率为0，这与图10（a）中的结果一致.

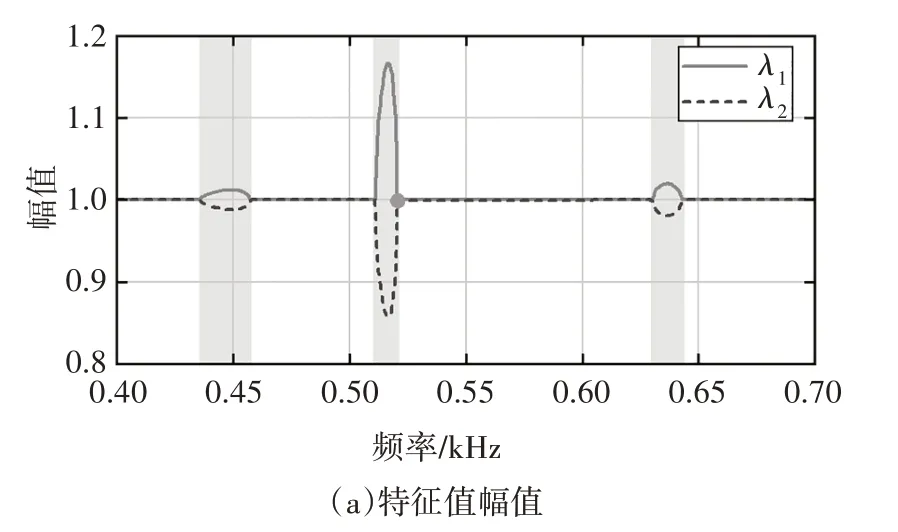
图12 特征值幅值及相角Fig.12 The amplitude and phase angle of eigenvalues

图13 特征向量实部和虚部Fig.13 The real and imaginary parts of the eigenvectors

3 结论

1）利用压电分流单元设计一种针对弯曲波的PT 对称梁，其中压电分流单元连接了正∕负电阻并联电感组成的分流电路，构成损耗单元、增益单元；采用等效介质法计算损耗单元、增益单元的等效弯曲刚度和等效质量密度，并通过有限元仿真对等效介质法进行验证.结果表明，本文所提出的设计满足等效质量密度和等效弯曲刚度共轭对称.

2）采用传递矩阵法计算PT 对称梁的透射系数和反射系数，并与有限元仿真的结果进行比较，验证传递矩阵法的正确性.传递矩阵法和有限元仿真的结果表明，所提出的PT 梁针对弯曲波具有非对称散射特性，并且存在单向无反射点.

3）通过计算散射矩阵的特征值与特征向量，分析PT 对称梁的奇异点与单向无反射点之间的关系，结果表明，PT对称梁的奇异点即为单向无反射点.