基于AUPF 算法的水下履带车动力学参数估计

陈昱衡，吴鸿云，边有钢†

（1.湖南大学汽车车身先进设计制造国家重点实验室，湖南长沙 410082；2.长沙矿山研究院有限责任公司，湖南长沙 410012；3.国家金属采矿工程技术研究中心，湖南长沙 410012）

位于4～6 km 水深的深海底，其表层沉积物中以半埋藏状态覆存着大量的多金属结核矿产资源，因其富含锰、铜、钴、镍等稀贵金属元素，极具商业开采价值.20 世纪70 年代，以美国为首的西方发达国家率先开始深海采矿技术研究，完成了不同程度的试验，催发了一轮深海采矿技术研究热潮［1］.

在深海采矿作业时，采矿车沿着预设轨迹进行自行式采集结核，需要在线获取采矿车的动力学参数.然而，多金属结核矿区表层含水量高，承载力弱，易流动且伴随有海底不规则洋流的影响，导致多金属结核采矿车易发生履带沉陷和履带不规则打滑的现象［2］，故履带沉陷时采矿车的有效驱动轮半径应考虑履带板厚度和未陷入底质的驱动轮部分.若忽略驱动轮半径变化时履带打滑的动态响应，可能会对控制性能产生负面影响.因此，精准的履带打滑率和有效驱动轮半径等运动学参数估计显得尤为重要.

为解决上述问题，文献［3-6］基于RecurDyn 参数化建模技术，构建了多刚体深海采矿系统，完成了联动仿真分析，并对多金属结核采矿车的直行、差速转向、爬坡和越障等工况时的机械特性进行了仿真分析，并基于模型车进行试验以验证方案的可行性，为深海采矿系统的整体集成设计、性能预测及作业操控提供了参考，同时为多金属结核采矿车整车机械结构的优化设计提供了理论支撑［7-9］.

无迹卡尔曼滤波（Unscented Kalman Filter，UKF）算法通过无迹变换（Unscented Transformation，UT）将非线性函数模拟成真实分布的近似高斯分布，具有3 阶的泰勒精度，是一种易实现的参数估计算法［10-12］.周兵等［13］基于UKF 对非线性轮胎模型中的路面附着系数进行了在线估计，提高了自动驾驶车辆的主动转向控制性能.Qin 等［14］基于瞬时转向中心变化的履带车运动学模型，提出了一种改进的UKF 算法，实现了陆地自行式履带车辆履带打滑率的精准在线估计.

本文从多金属结核采矿车的受力分析出发，建立底盘液压驱动系统与履带负载特性的动力学关系，提出了多金属结核采矿车的有效驱动轮半径和履带打滑率等动力学参数的状态空间模型.针对UKF 算法无法在高非线性模型中得到较高估计精度的问题［15-16］，采用基于蒙特卡洛采样原理的自适应无迹粒子滤波（Adaptive Unscented Particle Filter，AUPF）算法进行多金属结核采矿车的动力学参数在线测算，利用自适应无迹卡尔曼滤波（Adaptive Unscented Kalman Filter，AUKF）算法改进概率密度函数以指导粒子滤波（particle filter，PF）进行重要性采样，克服了粒子滤波易发散的缺点［17］.试验结果表明，所提出的AUPF算法可实现多金属结核采矿车的动力学参数的精准在线测算.

1 多金属结核采矿车参数估计建模

1.1 多金属结核采矿车受力分析

与陆地履带车不同，多金属结核采矿车在多金属结核矿区稀软的底质上行驶，为了提高多金属结核采矿车的抓地能力，行走履带采用三角履齿.多金属结核采矿车如图1所示，三角履齿如图2所示.

图1 多金属结核采矿车Fig.1 Polymetallic nodules mining vehicle

图2 三角履齿Fig.2 Triangular track teeth

在计算采矿车履带产生的牵引力F时，不仅需要考虑履带对底质产生的剪切力F1，还需要考虑履齿剪切底质产生的压力F2.F1和F2分别见式（1）和式（2）.

式中：A为履带的接地面积，m2；W为车身正压力，N；c为底质内聚压力，kPa；φ为底质内摩擦角参数，(°)；l为履带接地长度，m；i为履带打滑率；k为底质水平剪切模变数，m.

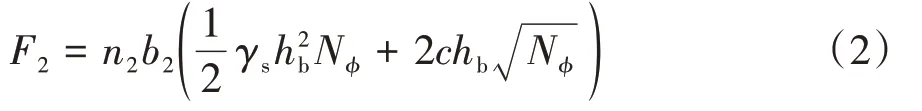
式中：b2为履齿宽度，m；γs为底质比重，kg∕m3；hb为履齿高度，m；Nφ=tan2(45°+0.5φ)为底质流值；n2为履齿个数.

牵引力F为：

1.2 多金属结核采矿车动力学参数在线测算模型

多金属采矿车在含水量高的稀软底质进行自行式作业时，底盘会发生沉陷现象，故实际的履带有效驱动轮半径ra为：

式中：r1为履带板厚度和履齿高度的和，m；r2为测高声呐测得的履带沉陷，m；r为理论驱动轮半径，m.

多金属采矿车左右履带驱动采用两独立的闭式液压回路，即采用两电动机分别驱动两变量泵，再经过定量马达传递到左右履带，马达直接驱动采矿车行走.其中液压马达的系统压力pl与马达的驱动力矩Tq呈线性关系，如式（5）所示.

式中：VM为液压马达的理论弧度流量，m3∕rad；pl为系统压力，Pa；θm为液压马达转角，rad；Jt为液压马达和负载总惯量，m·N·s2；Bm为负载和液压马达内部的总黏性阻尼系数，m·N·s∕rad；G为负载的扭矩刚度，m·N∕rad；ωm=dθm∕dt为液压马达转速，rad∕s；ω˙m=dωm∕dt为液压马达角加速度，rad∕s2.

多金属结核采矿车为低速匀速行驶，故在建模时可假设马达的负载力矩TL等于驱动力矩Tq：

驱动轮由液压马达直驱，故驱动轮转速ω等于液压马达转速ωm：

联立式（5）～式（7）负载力矩TL与驱动轮转速ω的方程，如式（8）所示.

同时驱动力矩Tq满足：

为了简化运算，基于文献［18］，对式（1）进行简化，得

联立式（2）式、式（4）、式（8）～式（10），可得到履带有效驱动轮半径和履带打滑率的关系.

通过离散化式（4）和式（10），定义如式（12）所示的状态空间模型.

状态量为：

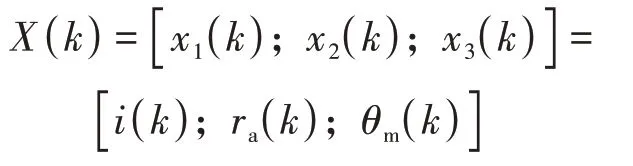
控制量为：

观测量为：

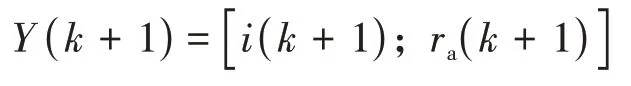
由于采矿车为低速行驶，故较小时间间隔内的平均速度可视为履带实际速度va.

式中：T为采样时间，s；L为每个采样时间T内的履带行走长度，m.

2 自适应无迹粒子滤波算法

粒子滤波算法不依赖高斯模型，基于蒙特卡罗采样原理，可应用于高线性系统的参数估计.但是PF 算法存在滤波易发散的缺点，通常采用UKF 算法指导粒子重采样以改进PF 算法.本文采用AUKF 指导粒子重采样的AUPF 进行参数估计.AUPF 的算法流程如表1所示.

表1 AUPF算法流程Tab.1 AUPF algorithm flow

AUKF算法的具体步骤如下：

1）初始化.

2）Sigma点权重计算.

式中：λ=n(α2-1)，α是控制Sigma 点分布的常数，其取值范围为e-4≤α≤1；β为非负常数，将高阶成分的信息转换到方差中，取β=2.

3）Sigma点选择和估计值更新.在UT中，随机变量由一组最小的样本点表示，称为Sigma 点.计算这些点在非线性系统模型传播时的后验平均值和协方差.Sigma点由式（16）计算.

粒子集合XAUPF(k)由式（23）计算.

式中：nrand为0～1的随机数.

粒子权重计算具体步骤如下：

1）计算观测值YAUPF(k).

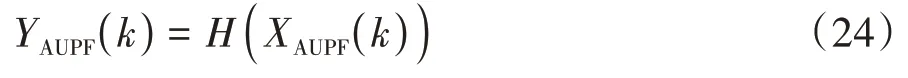
2）计算粒子权重并归一化.

通过设定权重阈值进行重采样并更新状态与基本PF算法一致，本文不再赘述，见参考文献［10］.

基于张滔等人［9］的研究，式（1）、式（2）中多金属结核底质土力学特性的参数值和采矿车动力学参数测算模型的参数如表2所示.

表2 模型参数值Tab.2 Parameter values of the model

3 动力学参数在线测算方法实验验证

为了验证本文提出的动力学参数测算算法能否精准测算多金属结核采矿车的履带打滑率和有效驱动轮半径，定义如下性能需求：有效驱动轮最大误差不超过5 mm，履带打滑率的最大误差不超过5%.以上述多金属结核采矿车为实验对象，在深海采矿实验水池进行行走实验，实验水池长60 m，宽50 m，深5 m，实验室水池如图3所示.

图3 实验室水池Fig.3 Laboratory sink

水池底质为河泥以模拟多金属结核矿区的稀软地形，水深保证可以淹没整个多金属结核采矿车.多金属结核采矿车通过起重机下放至水池中，由惯性导航单元和多普勒测速组成的水下组合导航系统使采矿车完成如图4所示的行走路线.

图4 采矿车实验行走路线Fig.4 Mining vehicle’s test route

测控主系统为美国National Instruments 公司推出的Compact RIO 嵌入式测控平台及软件.车载本地测控站采集并记录采矿车上各传感器检测参数，多金属结核采矿车搭载多普勒测速仪、光纤陀螺、履带驱动电机编码器、测高声呐等传感器实时获取采矿车的运动信息.光纤陀螺给出精准的采矿车的航向角φ和角速度ω′；履带驱动电机编码器给出采矿车带驱动轮的转速ω和加速度ω˙.

车载本地测控站记录所测算的外侧履带打滑率io、内侧履带打滑率ii、外侧有效驱动轮半径ro和内侧有效驱动轮半径ri的实验数据分别如表3 和图5～图8 所示.同时实际的驱动轮半径通过式（4）计算，实际打滑率由式（26）计算.

表3 运动参数均方差Tab.3 Mean square error of motion parameters

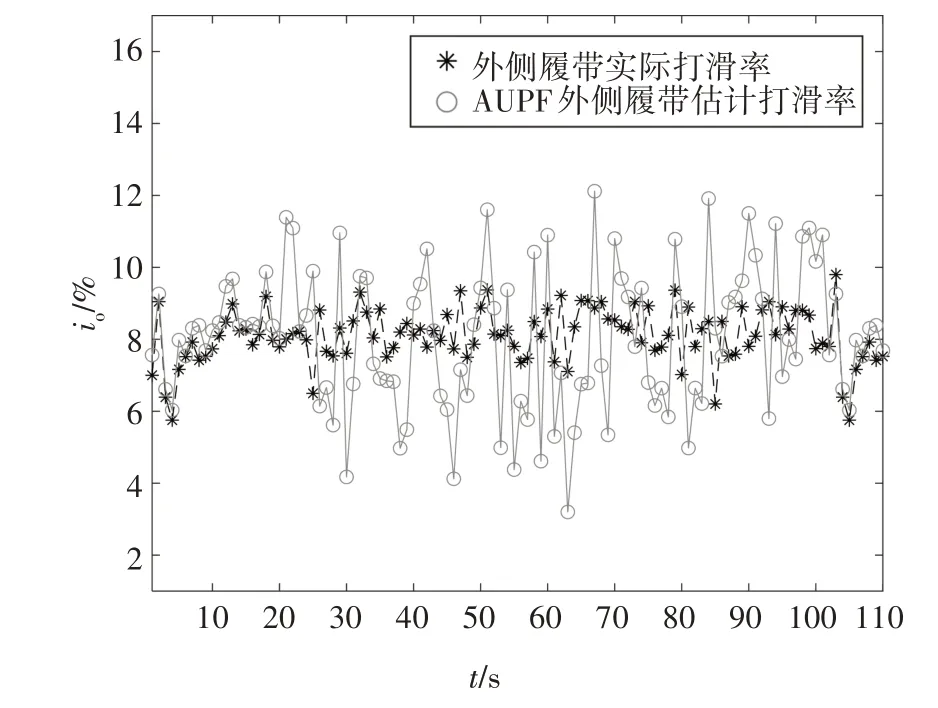
图5 外侧履带打滑率Fig.5 Lateral track skid rate

图6 内侧履带打滑率Fig.6 Medial track skid rate

图7 外侧有效驱动轮半径Fig.7 Effective radius of the lateral driving wheel

图8 内侧有效驱动轮半径Fig.8 Effective radius of the medial driving wheel

式中：va为履带实际速度，由式（13）计算.

由实验结果可知，有效驱动轮半径的误差在3 mm 以内，履带打滑率的最大误差不超过5%，有效驱动轮半径的误差均方差小于0.5，履带打滑率误差均方差小于1.5.

误差的产生可能是由于实验室模拟底质的力学特性与真实底质的力学特性有一定的差距，故状态空间模型中的底质力学特性与实验水池模拟底质的力学特性存在不匹配的情况.但是有效驱动轮半径的误差和履带打滑误差都小于最大误差，且均方差均较低.通过AUPF 算法可以得到精度较高的多金属结核采矿车动力学参数，同时说明AUPF算法对模型的不匹配情况也具有较好的适应性.

4 总结

针对多金属结核采矿车在海底行驶作业时，履带打滑率和有效驱动轮半径等动力学参数难以确定的问题，本文通过分析多金属结核采矿车的履带牵引力和履带的液压负载特性，建立了多金属结核采矿车履带打滑率和有效驱动轮半径等动力学参数在线测算的状态空间模型.针对动力学参数测算状态空间模型非线性程度较高的问题，提出了利用AUPF算法进行多金属结核采矿车动力学参数测算的方案.实验结果表明，有效驱动轮半径的误差控制在3 mm 以内，打滑率的最大误差不超过5%，满足动力学参数测算的精度要求，验证了所提方案的可行性，具有重要的工程应用价值.