基于加点多目标粒子群算法的碳纤维防撞梁优化设计

陈静，崔晓凡，郑晋军，徐森，胡金旭

（吉林大学汽车仿真与控制国家重点实验室，吉林长春 130025）

随着全球性资源短缺和环境污染的日益严重，各国政府越来越关注汽车的节能减排问题.研究表明，汽车每减重10%，燃料消耗可以降低6%～8%［1］，因此，车辆轻量化成了降低油耗和减少排放的重要手段之一.碳纤维等新型复合材料相比传统金属材料具有质量轻、强度高等优点，在汽车轻量化中得到了广泛应用［2］.保险杠防撞梁作为汽车主要的被动安全件，在进行轻量化设计的同时要兼顾质量减少对其性能的影响，国内外学者在防撞梁的轻量化设计方面做出了许多工作.

仲伟东等［3］将碳纤维防撞梁的铺层数和部件厚度作为设计变量，采用响应面模型，利用多目标遗传算法对防撞梁进行了优化设计，实现了减重13.9%.张鑫等［4］建立了碳纤维防撞梁的低速碰撞模型，采用Hyperkriging 模型和遗传算法对单层碳纤维厚度进行了优化，相比钢制防撞梁减重达到71.4%.Nursherida 等［5］对钢、玻璃纤维和碳纤维防撞梁进行了建模和低速碰撞仿真，结果表明碳纤维防撞梁比吸能量最高，能显著降低防撞梁质量.Godara 等［6］设计了8 种不同的碳纤维防撞梁截面形状，进行的正面低速碰撞仿真表明，除了“B”字形截面外，开放截面的应力和位移值都高于封闭截面，为轻质复合材料防撞梁的截面设计提供了参考.

在上述变厚度防撞梁设计中，往往事先对不同厚度下的铺层顺序进行统一假定，并未考虑到铺层顺序与厚度之间的耦合关系，这导致了厚度不同的各部分之间铺层连续性较差，防撞梁性能下降.另外，在对防撞梁厚度进行多目标优化时，采用单向的试验设计、近似模型构建、优化算法的优化步骤，一旦近似模型精度不够，就需要重新抽样进行试验设计和近似模型构建，费时费力.

本文对碳纤维材料防撞梁进行结构优化设计.首先，通过全因子试验确定防撞梁截面参数，基于等刚度原理确定防撞梁厚度的取值范围.其次，根据防撞梁不同区域之间的铺层相容性和复合材料的基本铺层原则确定铺层顺序.最后，利用基于kriging模型的加点多目标优化算法对铺层厚度进行优化，其中，kriging 模型对预测偏差的估计和加点策略的结合有效解决了重复试验设计的问题，提高了优化效率.

1 碳纤维防撞梁结构初步设计

1.1 碳纤维防撞梁截面形状设计

根据工程经验［7］，常见的防撞梁截面多为“目”字形或“日”字形，但考虑到碳纤维层合板需要进行铺层加工的特点，上述两种形状无法在其闭合截面内部进行铺层.因此，初步确定防撞梁截面形状为开放的“B”字形.

本文碳纤维前防撞梁的长、宽、高参数参考某轻型乘用车钢制防撞梁，根据具体结构的不同，“B”字形截面包括图1所示的两种形状，其中截面参数a和b为主要设计参数.以防撞梁前端面C 作为因素b的零水平位置，假设左侧截面参数b取值为负，右侧截面参数b取值为正，对a、b进行全因子试验设计得到最优的截面参数组合.表1为参数a、b全因子试验因素-水平表.

图1 “B”字形截面的不同形状Fig.1 Different shapes of“B”section

表1 参数a、b全因子试验因素-水平表Tab.1 Full factor test level table for parameter a，b

根据不同截面参数，构建包括碰撞器、碳纤维防撞梁、钢制吸能盒和前纵梁在内的汽车前端结构碰撞有限元模型，如图2所示.为模拟真实碰撞情况，将车辆的整备质量1 400 kg赋予到前端结构的网格节点上.根据《汽车前、后端保护装置》（GB∕T 17354—1998）［8］中对汽车正面低速碰撞的规定，试验车辆碰撞速度控制在4 km∕h，碰撞器为与试验车整备质量相等的刚性壁障，前端面保持垂直、基准线保持水平.碰撞试验后，试验车满足照明和信号装置仍能正常工作，发动机罩、行李箱盖均能正常开闭.在LSDYNA 软件中构建低速碰撞仿真工况，评价防撞梁碰撞性能的参数分别为最大吸能量、侵入量和吸能盒截面碰撞力.得到试验数据后，进行极差分析，结果如表2所示.

图2 汽车前端结构碰撞有限元模型Fig.2 Finite element model of automobile front end structure in collision

表2 全因子试验结果Tab.2 Full factor test results

由极差分析结果可以看出，各个性能指标之间存在矛盾，如果片面追求某一个指标的最优，则会导致其他性能的下降.因此，采用综合平衡法分析各组合对性能的影响，选取所有性能指标均较好的组合：

1）相比参数a，参数b对防撞梁碰撞性能的影响较大；

2）当参数组合选择a3b2时，最大截面碰撞力达到16.365 kN，为全因子试验中碰撞力指标最差的组合，因此参数b选择b4；

3）对比a3b4、a4b4两组性能指标，可以看出a4b4组合侵入量和最大吸能量都较好.

最终确定a4b4为防撞梁截面的最优参数组合，即a取480 mm，b取-50 mm.

1.2 基于铺层约束的铺层顺序确定

为了更好地实现车辆轻量化，根据各部分对碰撞性能的影响程度，将“B”字形防撞梁划分为前板、后板、上板、下板4 个铺层区域，各区域采用不同的厚度，如图3所示.

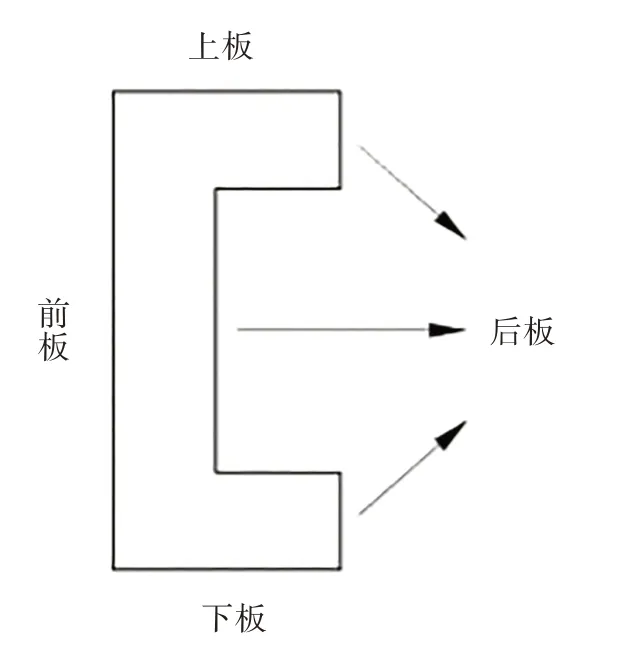
图3 防撞梁铺层区域划分Fig.3 Area division of anti-collision beam

在薄板件的轻量化设计中，可以通过材料替换后刚度保持不变的等刚度原理进行厚度的初步确定［9］，如式（1）所示：

式中：δt为材料替换后与替换前的厚度之比；t0、t1分别为材料替换前、后的零件厚度；E0、E1分别为原材料与替换材料的弹性模量；η为厚度指数系数，取值范围一般为1～2，这里η取2.

本次设计中选择的碳纤维材料为日本东邦STS40，单层厚度为0.2 mm，弹性模量为152 GPa；已知原钢制防撞梁的厚度为1 mm，钢材的弹性模量为235 GPa，根据式（1）可以确定碳纤维防撞梁的基本厚度为1.2 mm.

对于碳纤维复合材料而言，决定其力学性能的主要因素是厚度和铺层角度，工程中常用的铺层角度分别为0°、45°、-45°、90°.由于各个铺层区域的厚度不同，如果对每个区域都单独进行铺层角度设计，那么连接位置没有碳纤维材料过渡，仅靠树脂黏接，性能会严重下降.因此，进行铺层角度设计时需要尽量使多个区域共享同一层纤维，结合复合材料的基本铺层原则［10-12］，提出以下几条铺层约束：

1）对称性约束：铺层关于中间面对称.

2）表面连续性约束：各区域表面的铺层连续.

3）相邻丢层数约束：相邻区域的铺层丢层数不能超过4层.

4）铺层相容性约束：各区域应最大限度地共享铺层.

5）层数连续性约束：铺层角度相同的连续层数不能超过3层.

6）均衡性约束：±45°应尽量成对出现.

7）最小比例约束：为使材料基体沿各个方向都不受载，任一方向最小铺层比例≥10%.

8）抗冲击约束：在表面铺设±45°层可以改善层合板的抗冲击性能.

碳纤维材料的铺层特性决定了防撞梁的厚度取值是离散的，综合考虑轻量化效果和最大化碰撞性能，确定厚度取值分别为1.2 mm、1.6 mm、2.0 mm、2.4 mm，根据以上铺层约束确定对应的铺层顺序如表3所示，全部为对称铺层.

表3 各铺层厚度下的铺层顺序Tab.3 Stacking sequence for each ply thickness

2 碳纤维防撞梁铺层厚度多目标优化

铺层顺序确定后，仍需确定各区域厚度的具体取值.由于防撞梁需要满足的性能指标有多个，因此，厚度优化是一个多目标优化问题.本次设计中提出一种基于kriging 模型的加点多目标优化算法，利用kriging 模型对预测偏差进行估计，并结合加点策略不断更新样本点，对设计空间进行补充，在少量抽样的前提下达到收敛最优解的目的.

2.1 基于kriging 模型加点策略的多目标粒子群算法

2.1.1 kriging近似模型构建

在多目标优化问题中，当真实数学模型无法构建时，往往需要采用长时间的高精度分析计算来得到目标值，造成优化效率低下，这时近似模型的应用是一种提高效率的有效方法.常用的近似数学模型包括响应面模型、神经网络模型、kriging 模型等［13］，其中，kriging 模型在近年得到广泛应用，其优势在于对目标值进行预测的同时还能实现对预测偏差的估计.

为方便试验，将各铺层区域厚度定义为优化变量，其中上板、下板、前板和后板厚度依次为变量x1、x2、x3、x4，且变量x的取值分别为1.2 mm、1.6 mm、2.0 mm和2.4 mm.为保证初始kriging模型的精度，本次试验设计次数为60 组.限于篇幅，仅列举部分最优拉丁超立方试验设计结果，如表4所示.

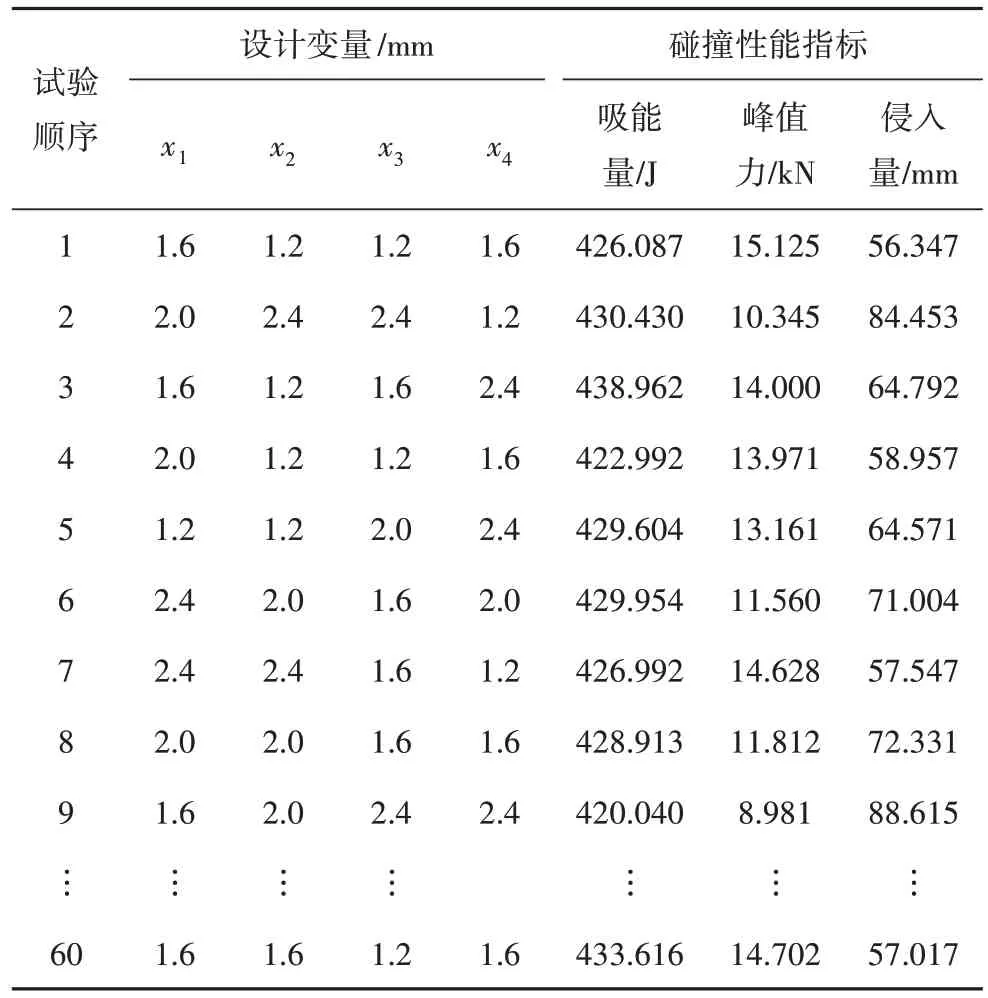
表4 铺层厚度最优拉丁超立方试验设计Tab.4 Optimal Latin hypercube test design for ply thickness

采用kriging 模型构建防撞梁各铺层区域内厚度与防撞梁侵入量、最大吸能量和峰值力之间的函数关系，由于质量不受碰撞仿真影响，仅与铺层厚度和铺层区域有关，故可以直接精确构建铺层区域内厚度与防撞梁的质量函数，不必构建近似模型.

2.1.2 结合加点策略的多目标粒子群算法

对铺层厚度多目标优化来讲，碰撞过程为高度非线性，而碳纤维材料设计也具备较高的非线性，这就导致碳纤维防撞梁设计变量与性能响应之间为高度非线性的函数关系.而试验设计次数由主观确定，一旦试验设计次数不足，导致近似模型精度不够，则会消耗大量的时间与精力重新进行试验设计.

现有的全局优化方法如基于代理模型的多目标EGO 全局优化算法就避免了对近似模型精度的检验［14］，其主要原理为利用代理模型，在每次迭代寻优过程中更新试验点对原有设计空间进行补充，最终达到收敛最优解的目的，但其缺点是计算复杂、优化效率较低.

通过上述分析可知，结合传统群智能多目标优化算法和基于代理模型的多目标EGO全局优化算法各自的优点，以kriging 模型为纽带设计一套高效、低误差的多目标粒子群优化算法很有必要.

基于kriging 模型加点策略的粒子群算法主要包括初始化粒子信息、支配关系比较、领导粒子更新、粒子变异、加点、收敛条件判断、最优解选取等步骤，其中加点策略的应用在减少重复试验设计的前提下保证近似模型预测的准确性.

初始化粒子速度为零，位置为介于变量取值范围内的随机值.迭代开始后，首先对各粒子的速度和位置信息进行更新，如式（2）、式（3）所示.其中，w为惯性权重，c1为个体学习权重，c2为种群学习权重，x_pbest(i)为第i个粒子的个体最优位置，x_gbest(i)为第i个粒子的全局最优位置，x(i+1)为粒子迭代更新后的位置.

计算更新后粒子的适应度，并与原个体最优位置进行支配关系比较，得到更新后的个体最优位置.在个体最优位置更新后再进行支配关系比较，从此次支配占优的个体与初始化占优个体的相互支配关系中得到非支配解集.

为了获取新的全局领导者，需要计算非支配解集的拥挤距离，如式（4）所示.

式中：m为目标函数的个数和分别为第i-1个粒子和第i+1 个粒子的第j个目标函数值和为第j个目标函数的最大值和最小值.在非支配解集中拥挤距离较大的前20%中随机选取个体作为全局领导者.

求解初期，要保证算法有较大的搜索性能，因此变异率应高一些；求解后期，变异率应低一些以保证算法的发掘性能.粒子变异公式如式（5）所示.

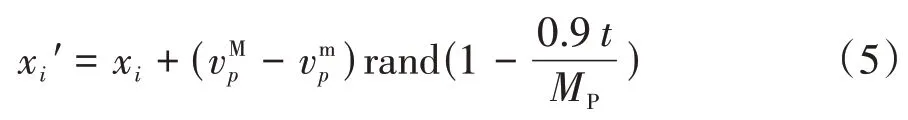
式中：xi′为变异后的粒子位置分别为第i个粒子的第p个速度上、下限；t为当前迭代次数；MP为迭代总次数.

为避免出现由于kriging 近似模型精度不够导致的重新抽样、重新仿真及构建近似模型的问题，每次迭代完成后，在储备前沿解集中依据加点准则选取样本点，仿真获得真实响应加入近似模型的构建中，这样不仅能保证优化结果的精度，而且能避免计算资源浪费，提高效率.根据EIM 加点准则构造EI 函数如式（6）所示［15］：

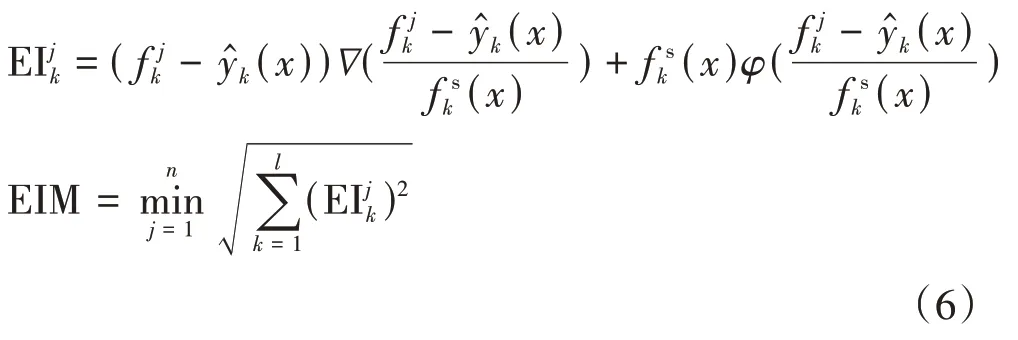
迭代收敛后，采用逼近理想解排序法（Topsis法）在Pareto 解集中选取最优点.Topsis法是一种根据逼近理想解的程度来评估各解优劣等级的多目标决策方法［16］.通过对Pareto 解集中各点的归一化处理得到分析数据矩阵，确定各评价指标的最优与最劣解向量.

式中：zij为各点归一化处理后的指标值分别为各指标最优、最劣值向量分别为各点与最优、最劣值向量之间的距离；Ci为各点与最优值的相对接近度.根据式（7）计算各点与最优值的相对接近度，某点相对接近度越大，越接近最优值.因此，对相对接近度进行排序，可以得到最优解.

基于kriging 模型的加点多目标优化算法流程如图4所示.

图4 基于kriging模型的加点多目标优化算法流程Fig.4 Multi objective optimization algorithm flow with adding points based on kriging model

2.2 基于加点粒子群算法的铺层厚度多目标优化

以各铺层区域的厚度x1、x2、x3、x4为设计变量，以防撞梁质量最小、碰撞峰值力最小和吸能量最大作为目标，以最大侵入量小于80 mm 作为约束，构建如式（8）所示的数学模型.其中，fF(x)为碰撞力，fM(x)为质量，fE(x)为吸能量，g(x)为侵入量.需要注意的是，这里将铺层厚度转变为连续变量进行优化求解，最后圆整到离散值上.

为使算法有较好的搜索能力，设置粒子群规模为300，最大迭代步数为30，经过10 轮加点优化，最终得到的Pareto解集如图5所示.

图5 铺层厚度最优Pareto解集Fig.5 Optimal Pareto solution set of ply thickness

采用Topsis 法并结合铺层厚度的实际取值空间，确定最优解为［1.2 mm、1.2 mm、2.0 mm、1.6 mm］.

将优化后的厚度值代入有限元模型进行低速碰撞仿真，碰撞性能与优化前防撞梁的对比如表5 所示.由表5 可知，仅进行材料替换后，碳纤维防撞梁的最大吸能量和侵入量得到了改善，但碰撞力需要进一步进行结构优化.进一步结构优化后，防撞梁的碰撞力下降，碰撞性能得到进一步提高，满足低速碰撞要求；同时，原钢制防撞梁质量为2.32 kg，优化设计后的碳纤维防撞梁质量仅为1.216 kg，减重率达47.59%，轻量化效果明显.

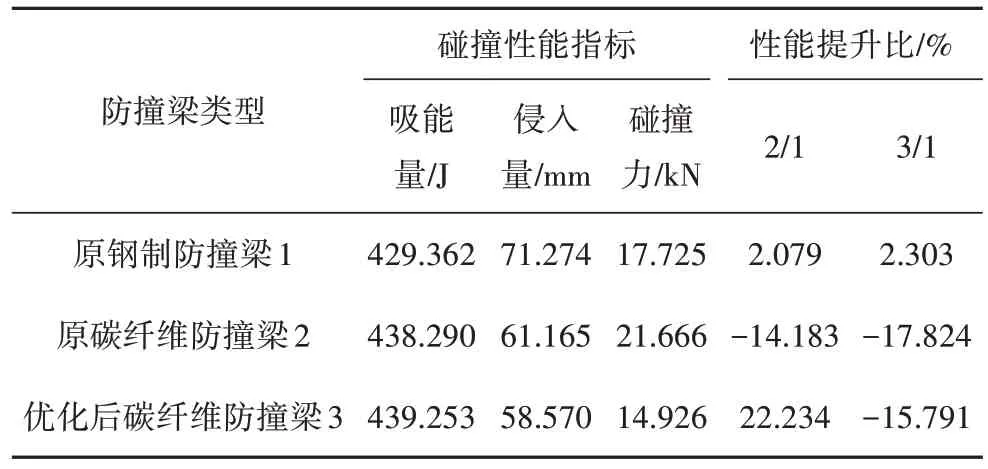
表5 优化前后防撞梁低速碰撞性能对比Tab.5 Comparison of low speed impact performance of three kinds of anti-collision beams

3 碳纤维防撞梁台车试验验证

碳纤维防撞梁结构设计完成后，采用模压工艺进行样件制作，样件表面光洁、无褶皱、无气泡，质量得到了保证.经过称重，碳纤维制件的质量为1.23 kg，与设计的1.216 kg误差仅为1%.

为验证优化后的防撞梁性能，对防撞梁制件进行低速台车碰撞试验，由于试验条件有限，用刚性墙替代国家标准中的碰撞器.低速碰撞仿真中吸能盒与防撞梁之间为黏接，台车试验时，为了保证复合材料与金属之间连接的可靠性，两者之间采用胶黏和铆接相结合的方式进行连接.通过焊接将吸能盒后端和工装夹具进行连接，并将整个前端结构用螺栓固定在试验台车上，与仿真中吸能盒与后端纵梁之间的焊接相对应.为了模拟汽车碰撞时的真实情况，台车配备1.4 t的质量块.台车和质量块如图6所示.

图6 低速碰撞试验台车Fig.6 Low speed impact test bench

试验开始后，台车以4 km∕h 的速度碰撞刚性墙，为了获取防撞梁的侵入量等性能参数，在台车中部安装加速度传感器，用来记录加速度变化，并通过高速摄像机观察碰撞过程.

为了与台车试验条件保持一致，将有限元模型中的碰撞器改为刚性墙并修改边界条件进行低速碰撞仿真，得到的防撞梁碰撞力曲线如图7所示.由图7可知，曲线趋势基本一致，仿真工况下，防撞梁最大碰撞力为27.716 8 kN，试验最大碰撞力为24.908 0 kN，误差仅为11.28%.防撞梁碰撞侵入量曲线如图8 所示，由图8 可知，最大侵入量误差为6.69%.通过以上对比，碳纤维防撞梁在低速碰撞工况下的性能得到了有效验证，优化效果显著.

图7 仿真与试验碰撞力对比Fig.7 Comparison of impact force between simulation and test

图8 仿真与试验侵入量对比Fig.8 Comparison of intrusion volume between simulation and test

4 结论

为了探索复合材料在汽车零部件上的应用以更好地实现车辆轻量化，本文对碳纤维材料防撞梁的结构进行了优化设计.通过试验设计确定截面参数的前提下，利用等刚度原理确定厚度空间，考虑各区域铺层相容性并结合复合材料的铺层原则，确定各厚度下的铺层顺序，减弱了变厚度区域之间铺层的不连续性.采用基于kriging 模型的加点多目标粒子群算法对各区域的铺层厚度进行优化，其中加点策略的应用减少了重复试验设计，在保证精度的前提下提升了优化效率.对优化后的碳纤维防撞梁进行的仿真试验和台车试验均表明，碳纤维防撞梁的低速碰撞性能可以满足要求，优化设计取得了良好成效.考虑铺层连续性的铺层顺序设计和引入加点策略的多目标优化算法的结合，为复合材料零部件的设计提供了新思路.