基于卷积自编码网络的故障电弧多分类识别方法
2022-09-02李奎张丹王尧
李奎,张丹,王尧
(1.河北工业大学 河北省电磁场与电器可靠性重点实验室,天津 300130;2.河北工业大学 省部共建电工装备可靠性与智能化国家重点实验室,天津 300130)
0 引 言
电能在人们生产生活中应用广泛,随之而来的电气火灾事故也日益频发。据统计,由于电气原因引发的火灾占火灾总数的30%以上,其中故障电弧是引发电气火灾的重要原因[1-2]。串联故障电弧电流一般低于线路正常工作电流,线路中安装的断路器或熔断器等保护装置通常无法消除此类故障。非线性负载电流与故障电弧电流在时频域方面特征相似,导致故障电弧特征量选取困难[3]。因此,能否在非线性负载条件下准确检测出串联故障电弧,对于火灾防治至关重要。
由于故障电弧电流与电弧发生的位置无关,国内外很多学者通过提取电弧电流时频域特征并设置检测阈值实现了故障电弧识别。E.Tisserand等[4]利用线电流的导数作为特征量进行故障电弧诊断;G.Artale等[5]对电弧故障电流进行线性调频Z变换(chirp Z-transform,CZT),并利用变换后的低频谐波识别电弧故障;K.Koziy等[6]利用小波变换的多分辨率分析特点,分析电弧电流突变特征,通过自适应调整阈值方式实现了故障电弧辨识;王尧等[7]计算电弧电流变化率与有效值的比值,选取6~12 kHz频段的电流幅值作为时频域特征量,并设置检测阈值,所提方法简单易行;孙鹏等[8]基于小波变换多分辨率的特点,提出了小波熵值为阈值依据的串联型故障电弧检测方法,在电弧稳定与不稳定燃烧状态下有较高识别准确率;白辉等[9]提出了一种基于小波包变换与高阶累积量相结合的故障电弧识别方法,能够识别单一负载、组合负载以及支路电弧故障。阈值检测方法算法简便,易于硬件实现,但严重依赖于所设置的阈值大小,实际情况中非线性负载种类繁多,其工作特性存在较大差异,限制了阈值的泛化能力。
近年来,深度学习算法为故障电弧诊断提供了新思路,该方法无需人为设置阈值,通过训练神经网络模型自主形成故障电弧与正常工作的边界区分条件。苏晶晶等[10]应用经验模态分解提取电弧电流多个特征量,并构建概率神经网络模型进行故障电弧识别;J.E.Siegel等[11]应用傅里叶变换、梅尔频率倒谱变换以及离散小波变换对数据进行预处理,结合深度神经网络实现了故障电弧识别;杨凯等[12]应用分形维数对电流高频信号的混沌特性进行定量衡量,并通过盒维数与关联维数构造出故障电弧特征向量,最后采用支持向量机对其进行分类;WANG Yangkun等[13]基于时域和频域分析方法,利用全连接神经网络模型实现了故障电弧诊断。人工智能算法能在一定程度上解决阈值设置的问题,但现有方法常常需要人为提取电流数据特征作为网络模型的输入,增加了人为提取特征的工作量,此外,现有方法大多只进行故障电弧与正常工作的二分类研究,未进行负载类型识别。
本文结合卷积自动编码器(convolutional autoencode,CAE)与Softmax多分类器,构建一种卷积自编码网络模型。该模型以原始电流数据作为网络输入,无需人为提取特征量,能够同时检测故障电弧并识别负载类型,既具有卷积自动编码器的无监督特征学习功能,又具有Softmax多分类器的有监督多分类功能。
1 故障电弧实验数据采集与特征分析
1.1 故障电弧实验数据采集
根据GB/T 31143-2014《电弧故障保护电器的一般要求》搭建串联故障电弧实验平台,如图1所示。该实验平台包含点接触、碳化电缆两种电弧发生装置,其中点接触可以模拟接线端子松动、导体接触不良导致的故障电弧;碳化电缆可以模拟导线绝缘老化、绝缘击穿引起的故障电弧。
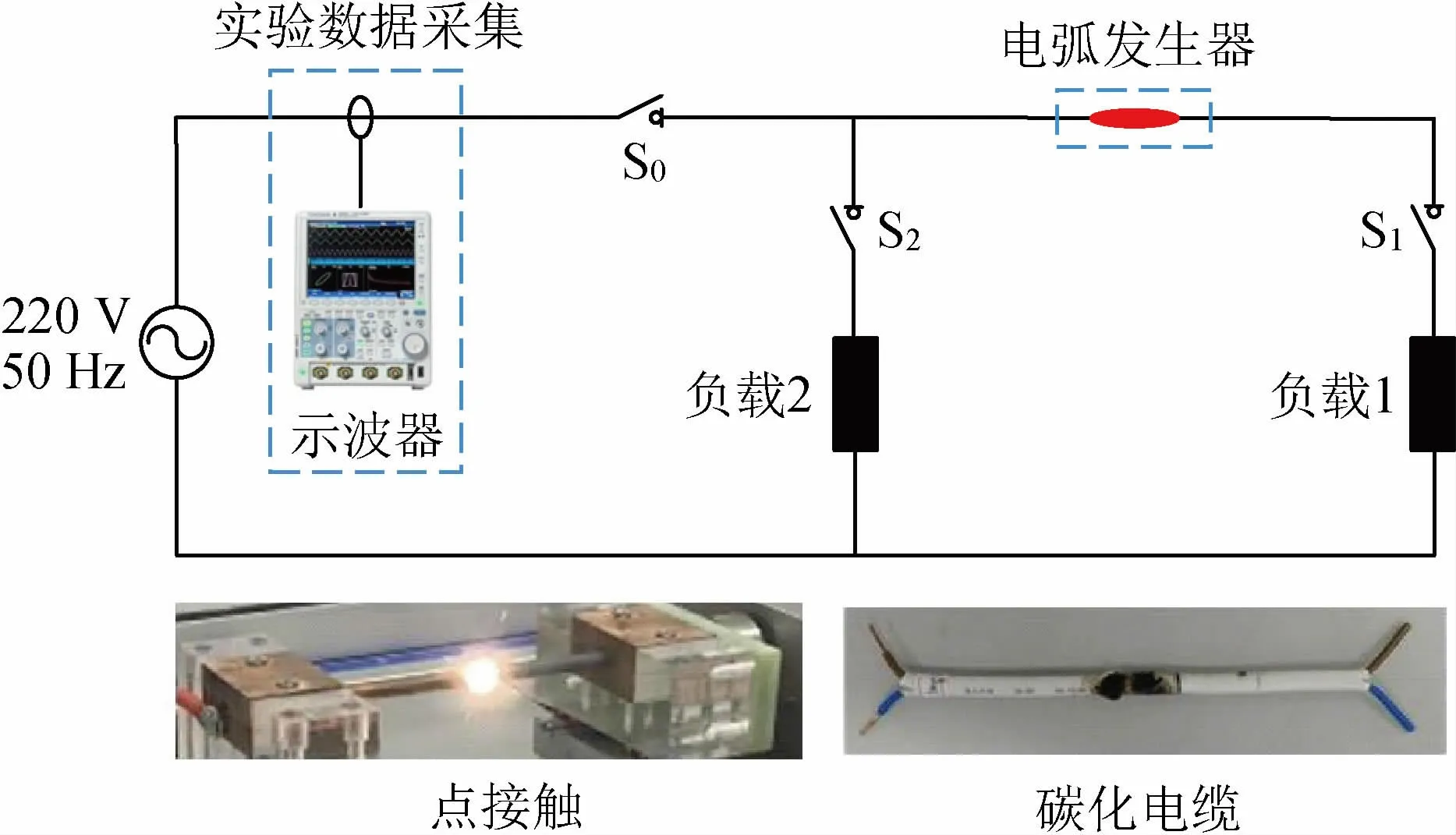
图1 故障电弧实验平台结构示意图Fig.1 Structure diagram of arc fault test platform
试验负载选取国家标准中规定的电阻、电容、启动电机、真空吸尘器等8种负载,负载参数如表1所示。使用数字示波器采集负载发生故障电弧前后的电流信号,采样频率设置为40 k Hz。
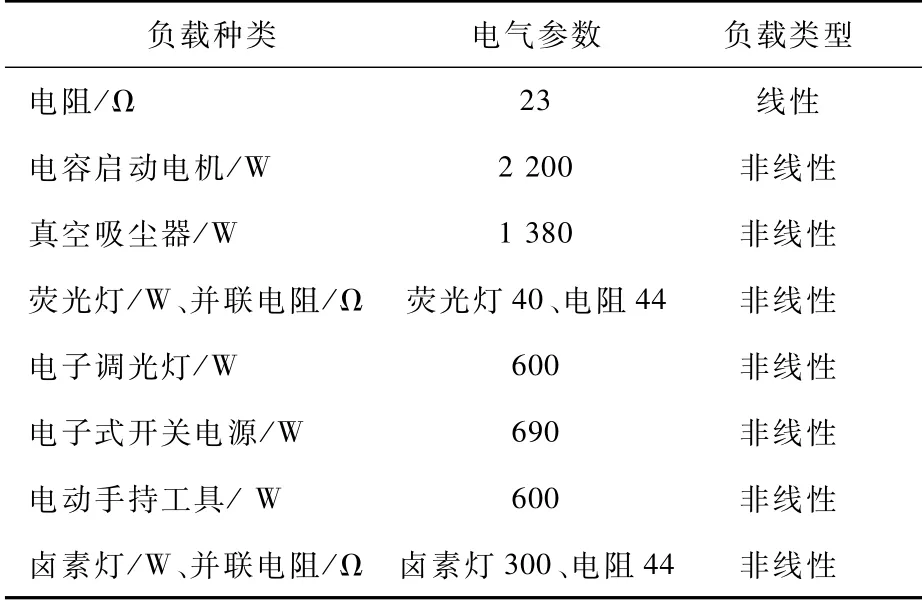
表1 实验负载参数设置Tab.1 Parameters setting of experimental loads
1.2 故障电弧电流时频域特征分析
以线性负载电阻、非线性负载电子调光灯、真空吸尘器为例,分析故障电弧电流的特征。图2为这3种负载正常工作与故障电弧状态的电流波形图。图2(a)中的电阻属于线性负载,正常工作状态下电流波形为平滑的正弦波,发生故障电弧时在电流过零点附近会出现零休现象,产生高频毛刺。图2(b)中的电子调光灯通过改变可控硅的触发角实现调光,正常工作时在电流过零点附近出现平肩部,容易与故障电弧的零休现象混淆。图2(c)中的真空吸尘器为电机启动类负载,通电后电动机高速旋转,内部电刷换向时电流波形在过零点附近发生畸变,其特征与发生故障电弧时的电流特征类似。
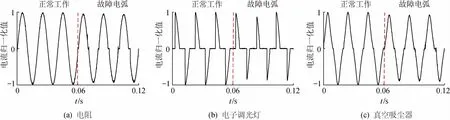
图2 典型负载正常工作与故障电弧状态下电流波形图Fig.2 Current waveform diagrams of typical loads under normal operations and arc fault states
电弧放电存在比较复杂的物理化学变化,不同负载下电弧电流差别较大,相同负载下电弧电流也不同。同时,某类负载正常工作时的电流波形可能与其他类负载发生故障电弧时的电流波形相似,导致故障电弧特征量选取困难,加剧了故障电弧的检测难度。自动编码器能够通过无监督学习,不断缩小重构数据误差,从而获取数据的深层特征[14],卷积神经网络利用卷积操作提取数据隐含特征,因此,本文将自动编码器与卷积神经网络结合形成卷积自动编码器,用于提取故障电弧电流数据特征。
2 卷积自编码网络的构成
2.1 卷积自动编码器原理
自动编码器利用自身高阶特征进行自我编码,能够挖掘出输入数据中隐含的特定结构[14]。卷积自动编码器在自动编码器基础上加入了卷积和池化运算,用卷积层代替自动编码器的全连接层。卷积神经网络的权值共享和局部感知特点可加快网络模型的计算速度,而自动编码器的无监督学习特点可减小网络发生过拟合的可能性。
卷积自动编码器包括编码器和解码器,通过不断缩小解码输出数据与原始输入数据之间的差异,使解码输出数据尽可能复现原始输入数据,其结构如图3所示。
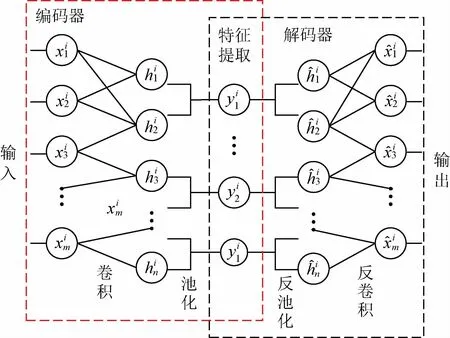
图3 卷积自动编码器示意图Fig.3 Schematic diagram of convolutional autoencoder
设卷积自动编码器中卷积层的输出特征为hi,第i个特征向量的卷积运算权值为wi1,偏置为bi1,用输入电弧数据xi训练卷积层的神经元,得到输出特征,f为激活函数。编码器中卷积层运算方程为[15]
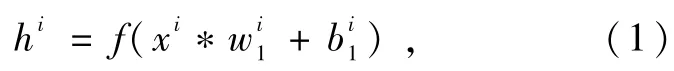
其中,*表示卷积运算,然后经过池化(下采样)运算
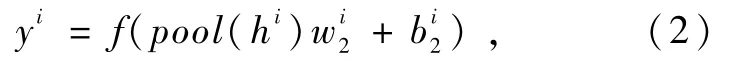
式中:pool(.)为池化运算,选用最大值池化方式;yi为池化运算输出结构;w2i为池化运算的权重为池化运算相应的偏置。输入数据经过卷积和池化运算提取出特征yi。
解码器是编码器的逆运算,用于重构输入数据,包括反池化与反卷积过程。其中,反池化进行上采样计算,为池化运算的反过程,用于恢复数据规模。反池化计算方程为[15]


2.2 激活函数和优化算法的选择
选用适合于深度网络学习的Relu激活函数,其表达式如式(5)所示,导数如式(6)所示。

Relu函数的函数输出值和导数输出值在输入数据小于0时恒为0;输入数据大于等于0时,函数输出值等于输入值,导数输出值恒为1,能有效避免梯度消失,有利于深度网络快速收敛。
选用均方根误差作为卷积自动编码器的损失函数,损失函数值代表了卷积自动编码器重构的电弧数据与输入的电弧数据之间的差异,其表达式为[16]
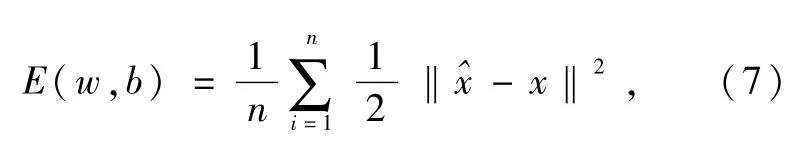
损失函数一般具有非凸及非平滑性特性,不能用解析方式求解。采用优化算法近似求解,更新网络参数,可不断近似逼近最优解。由于随机梯度优化方法样本选取随机,易发生震荡,且学习率设置过大时会导致网络不能收敛,学习率设置过小时又会导致收敛速度缓慢,因此,选择自适应矩估计(adaptive momentum estimation,Adam)优化算法,能够克服随机梯度算法通过单一学习率更新权重的缺陷[17]。
Adam优化算法基于方差思想,在网络反向传播过程中,计算梯度的一阶矩估计mt和二阶矩估计vt,根据不同参数设置不同学习率。第t次迭代时的mt和vt表示为
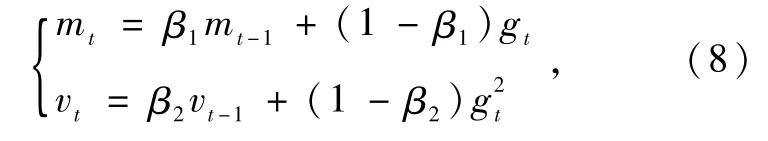
式中:β1为mt的指数衰减速率,将其设置为0.9;β2为vt的指数衰减速率,将其设置为0.999。此时,mt和vt为有偏估计,将其转换成无偏估计:
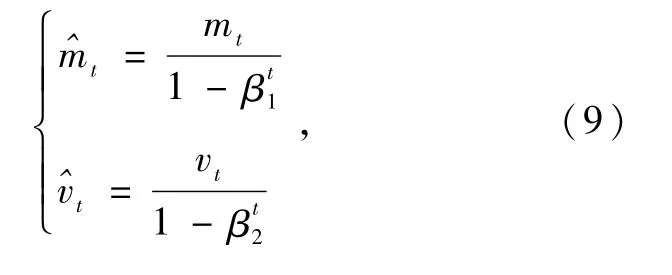
式中:βt1为β1在第t步计算的值;βt2为β2在第t步计算的值,取值为[0,1)。
3 故障电弧多分类识别方法
3.1 数据集制作
信号采集过程中不可避免会混入干扰信号,导致采集的电流数据出现异常点。为了确保同一类电流数据的一致性,需要对数据进行筛选,剔除不合理数据,主要包括实验设备原因造成的数据空值、电弧熄灭导致电流为0的数据等。选择一个工频周期的电流数据为一个样本,每个样本包括800个数据点,8种负载中每种负载正常工作和发生故障电弧的电流数据各600组,共计9 600组数据,训练集、验证集、测试集按4∶1∶1进行划分。为了避免不同负载电流值差异的影响,对电流数据归一化处理,采用离差标准化将电流值限制在[0,1]内,表达式为
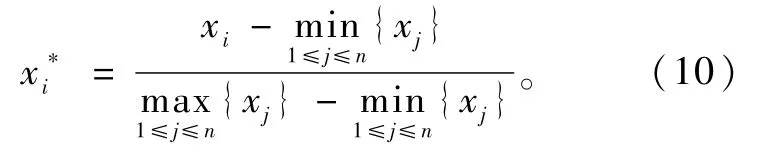
各负载标签设置如表2所示。
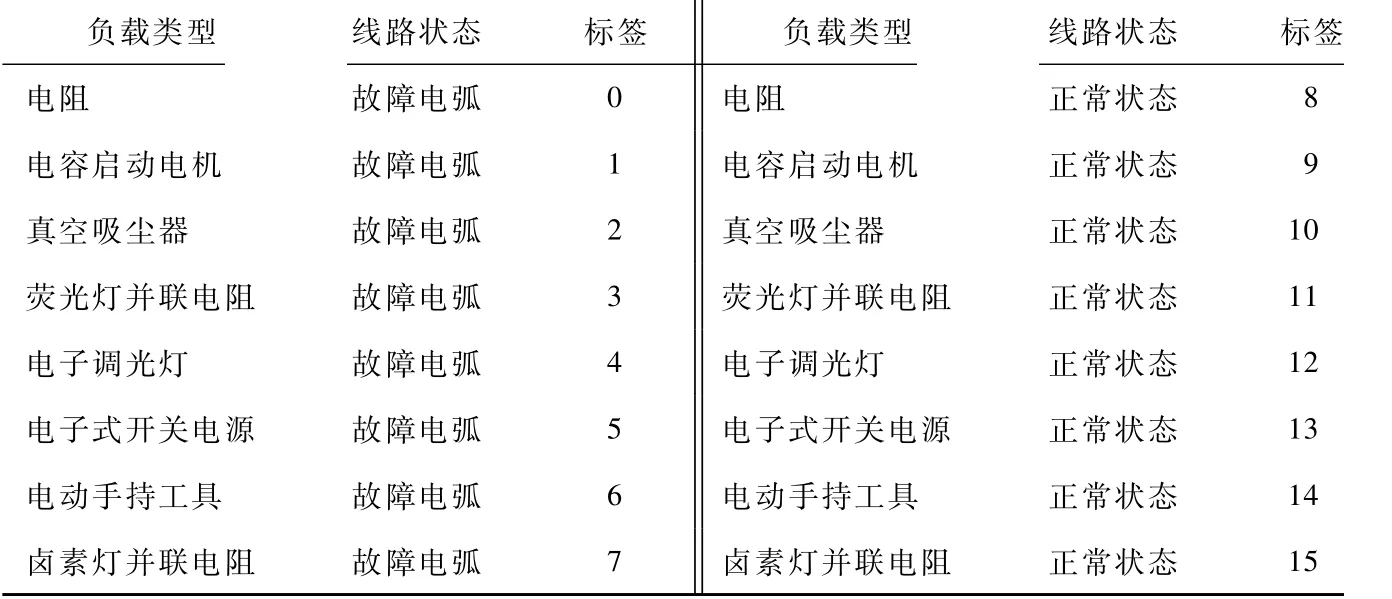
表2 负载标签设置Tab.2 Load label settings
3.2 用于故障电弧特征提取的卷积自动编码器 设计
输入无标签的数据集,经过编码器和解码器运算过程,使卷积自动编码器输出数据尽可能还原输入数据。卷积自动编码器重构误差反映了解码输出数据与原始输入数据之间的差异,重构误差越小,表示卷积自动编码器的解码输出数据能更有效地还原输入数据,可提取出输入数据中的深层特征[16]。基于Python中的Keras深度学习库搭建网络模型并进行实验研究,实验中网络结构参数选取方法如下。
3.2.1 卷积核尺寸选择
由于偶数卷积核尺寸在填充时难以保证输入特征向量与输出特征向量尺寸不变,卷积核尺寸通常设置为奇数[17]。卷积核尺寸为1时,相当于全连接网络,无法体现卷积优异的特征提取能力;而卷积核尺寸过大时,会大大增加模型参数计算量。因此,在其他参数固定的情况下,分别选取卷积核尺寸为3,5,7,评估卷积自动编码器重构数据的能力,实验结果如图4所示。
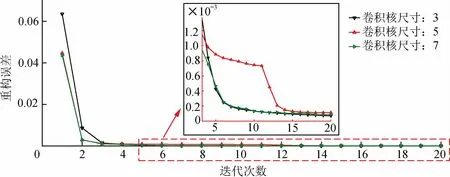
图4 卷积核尺寸的选择Fig.4 Convolution kernel size selections
卷积核尺寸为5时,损失函数值在训练初期下降明显,但在训练中期出现转折点,损失值下降缓慢;卷积核尺寸为3和7时,迭代20次左右即能达到相对较小的重构误差,考虑到大卷积核会增加网络模型参数,网络训练时间较长,因此,选取卷积核尺寸为3。
3.2.2 首层卷积核数量选择
实际应用中为了充分发挥计算机性能,首层卷积核数量通常设置为8的倍数,后续层按照首层的2倍倍增设置[17]。分别设置首层卷积核数量为8,16,32,实验结果如图5所示。
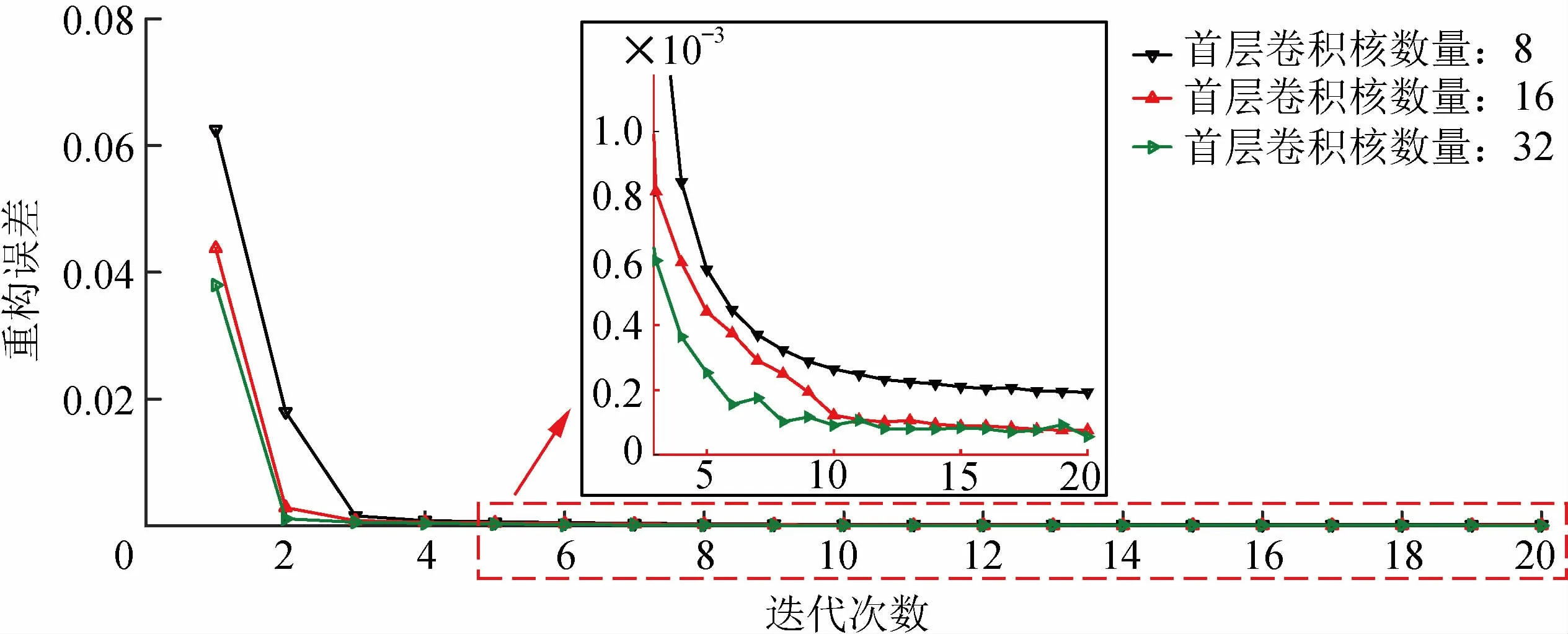
图5 首层卷积核数量的选择Fig.5 Selections of the number of first layer convolution kernels
卷积核可看作多个特征提取滤波器,能够从原始电弧电流数据中提取到有用特征,进行数据重构。数量较少时,卷积自动编码器不能有效学习和重构输入的电弧数据。首层卷积核数量为16和32时,训练20次左右重构误差能够很大程度降低。考虑到卷积核数量过多时会增加网络发生过拟合的可能性,选取首层卷积核数量为16。
3.2.3 池化比例选择
构建卷积自动编码器时,在卷积层后面设置池化层能够减少网络参数数量,加快计算速度,增强网络鲁棒性。池化层虽然能在一定程度上增强卷积自动编码器的泛化性能,但池化比例过高会导致网络丢失更多的特征信息,削弱网络提取特征的能力,所以池化比例的选择至关重要。考虑上述情况,本文设置池化比例分别为1,2,4,实验结果如图6所示。
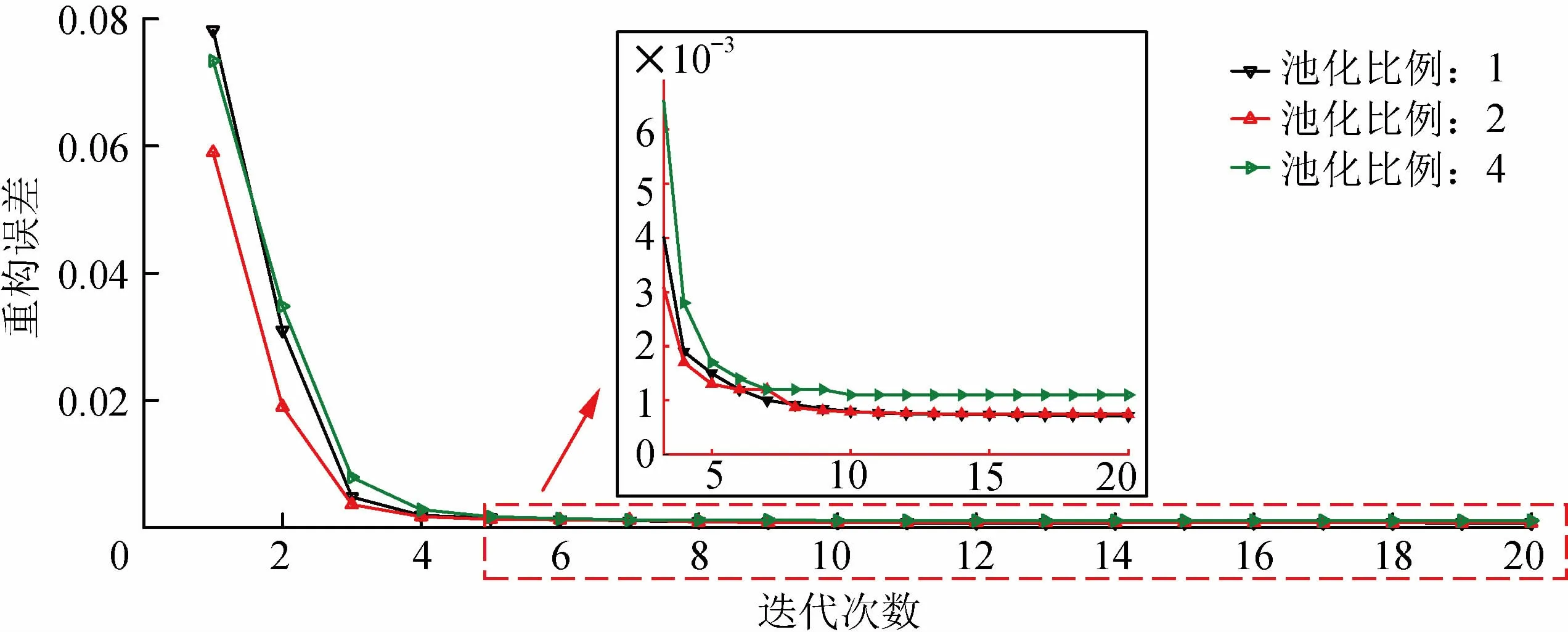
图6 池化比例的选择Fig.6 Selections of pooling ratio
池化比例为4时,由于池化比例过高,网络丢失了大量有用信息,导致提取到的电弧特征不具有代表性;池化比例为1时,即不进行池化运算,导致网络模型参数较多,训练时间较长。根据重构误差的收敛性,池化比例为2时能够加快网络收敛,并且重构误差较低。因此,选取池化比例为2。
3.2.4 卷积层数选择
随着卷积层数增多,得益于深度网络优异的学习性能,网络学习能力加强。但层数过多时容易出现过拟合现象,设置卷积层数分别为2,3,4,5,比较这4种卷积层数对卷积自动编码器的损失函数值的影响,实验结果如图7所示。
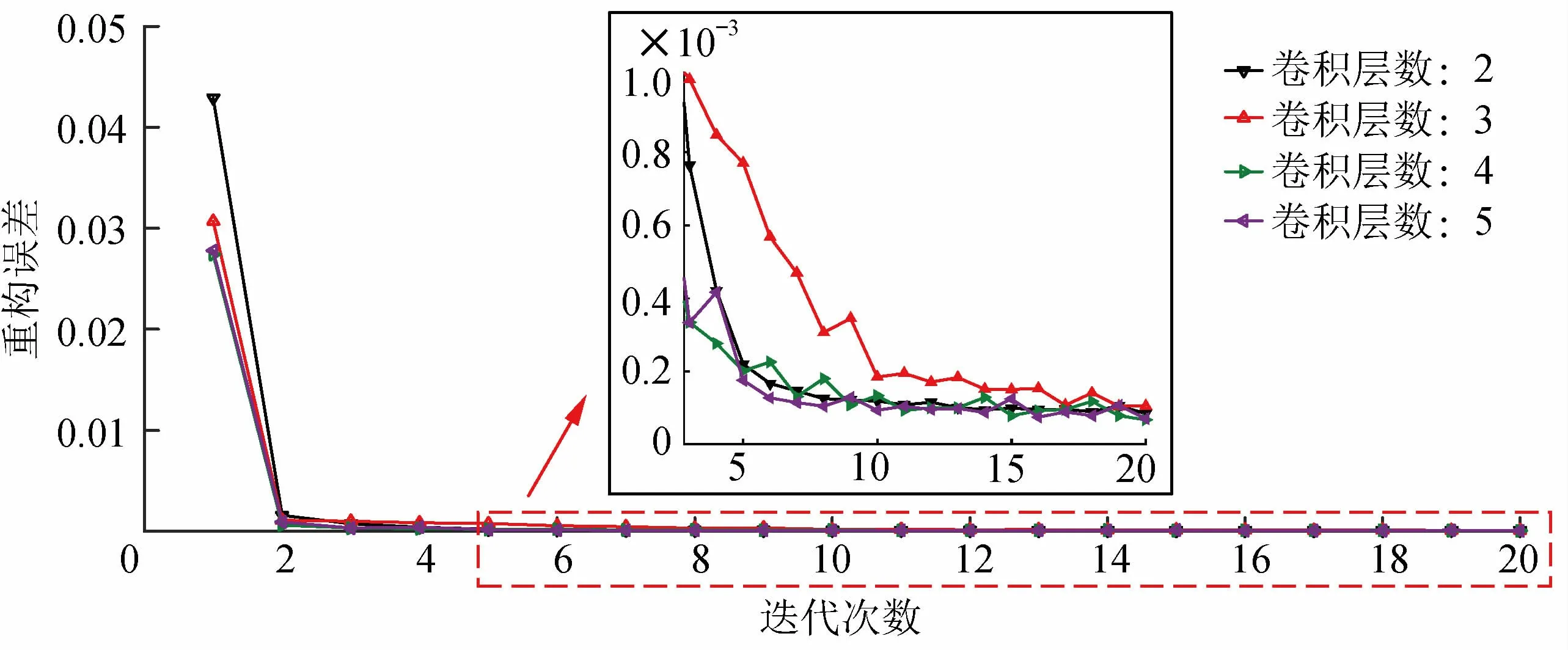
图7 卷积层数的选择Fig.7 Selections of the number of convolutional layers
卷积层数为4时,重构误差收敛较快,且最终收敛于一个较低值,卷积自动编码器提取到的电弧特征具有很强的代表性。卷积层数为5时,迭代初期损失函数起伏波动,且层数增多时训练时间大大增加。卷积层数为3时,迭代初期损失函数下降比较缓慢。卷积层数为2时,受限于网络深度的影响,不能有效学习到更充分的特征。因此,设置卷积层数为4。
选择4层卷积层构建卷积自动编码器的编码部分,每层卷积核尺寸为3,池化比例为2,首层卷积核数量为16,后续3层分别为32,64,128;解码部分与编码部分对称,设置4层反卷积层,每层反卷积核尺寸为3,反池化比例为2,首层反卷积核数量为128,后续3层分别为64,32,16。
应用无标签的电弧电流数据集对卷积自动编码器进行无监督训练,训练完成后,输入测试集样本进行测试。图8为真空吸尘器负载和电子式开关电源负载的编码器原始输入数据与解码器重构输出数据对比图。电流重构数据在一定程度上能够还原输入数据,电弧电流的“零休”特征得以保留。卷积自动编码器重构数据与输入数据差异较小,仅开头和末尾数据发生了微小波动,但负载正常状态和故障电弧的边界区分特征得以保留,重构数据的故障电弧波形不对称特征较为明显。因此,解码器重构数据能够有效还原原始输入数据,说明卷积自动编码的编码器输出数据能够有效表征输入数据的特征,利用卷积自动编码器提取的特征进行故障电弧多分类识别具有一定的可行性。

图8 原始数据与重构数据对比Fig.8 Comparison charts of raw data and reconstructed data
3.3 故障电弧多分类识别模型
基于卷积自编码网络的故障电弧多分类识别模型是将卷积自动编码器的编码器输出连接至一个多分类器,使得该模型既具有卷积自动编码器的深层特征提取功能,又具有多分类功能。选择逻辑回归模型中适用于多分类问题的Softmax多分类器。输入电弧电流样本{(x1,y1),(x2,y2),…,(xm,ym)},其中,xi为样本数据,yi为样本标签,取值0~15,代表16种分类结果。对于给定的电弧测试样本x,通过假设估计法计算出该样本属于16类中任意一类的概率p(y=j|x),假设函数将输出16维数据,分别表示该电弧样本属于这16类的概率。其中,假设函数表达式为
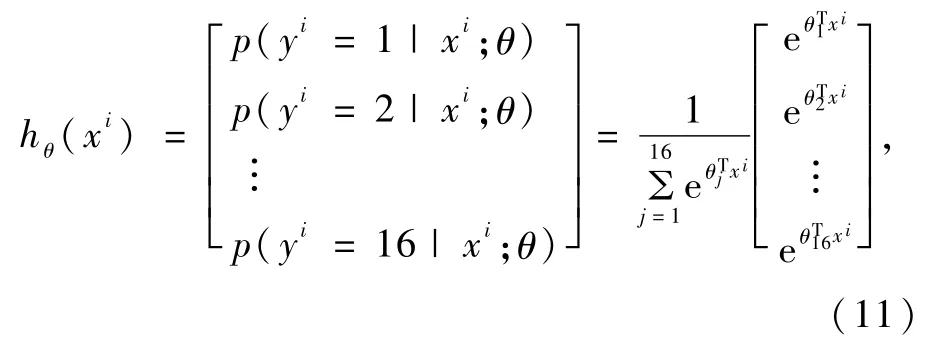
式中,θ1,θ2,…,θ16模型参数。
Softmax多分类器应用激活函数将各个输入向量映射到(0,1),所有输出映射值之和等于1,输入向量归属于输出值中某一类的条件概率最大的作为分类器输出结果。选择适用于多分类问题的交叉熵损失函数
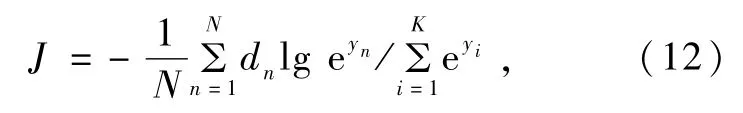
式中:dn,yn分别为第n个样本的真值与模型预测值;N为样本总数;K为类别总数。
卷积自动编码器训练完成后,去掉解码器部分,将编码器与Softmax多分类器相连。由于卷积自动编码器最后一层含有128个卷积核,使得编码器输出特征维度较高,而Softmax多分类器输出结果为16种类型,为了防止因为神经元个数急剧减少导致编码器丢失有效的电弧数据特征,在编码器最后一层池化操作后添加Flatten层,将其平铺融合,再添加一层全连接层作为编码器与多分类器之间的过渡层。
实验选取合适的全连接层神经元个数,分别设置全连接层神经元个数为0(不加全连接层),50,100,150,200,测得故障电弧多分类识别准确率如图9所示。随着全连接层神经元个数增加,网络的参数规模不断增加,结合识别准确率,设置全连接层神经元个数为100,此时模型识别准确率较高,相比于150和200两种情况下,节省了计算机内存,缩短了网络参数计算时间。多分类器使用样本标签数据可进行有监督学习。
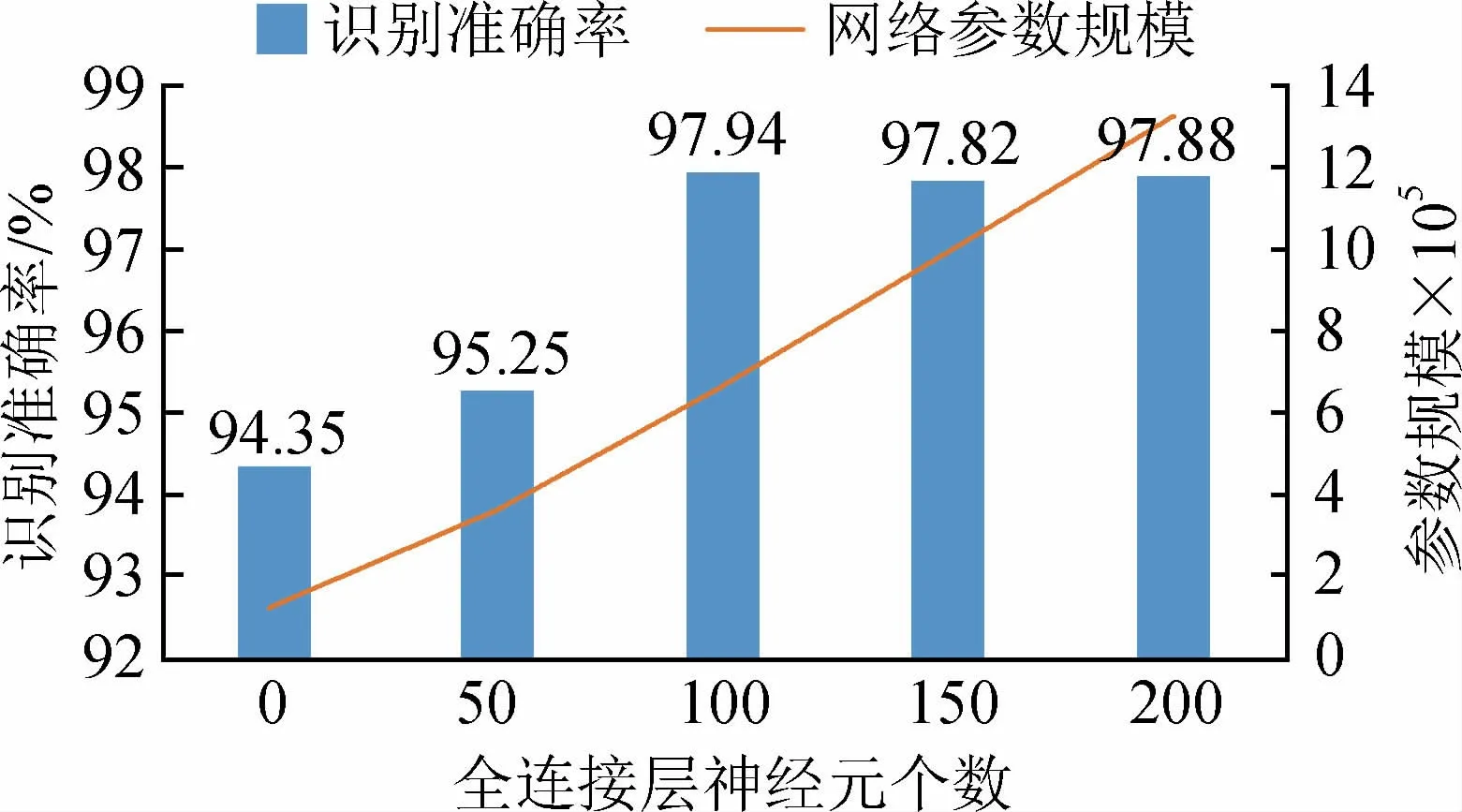
图9 全连接层神经元个数选择Fig.9 Selections of the number of neurons in the fully connected layer
故障电弧多分类识别模型如图10所示。
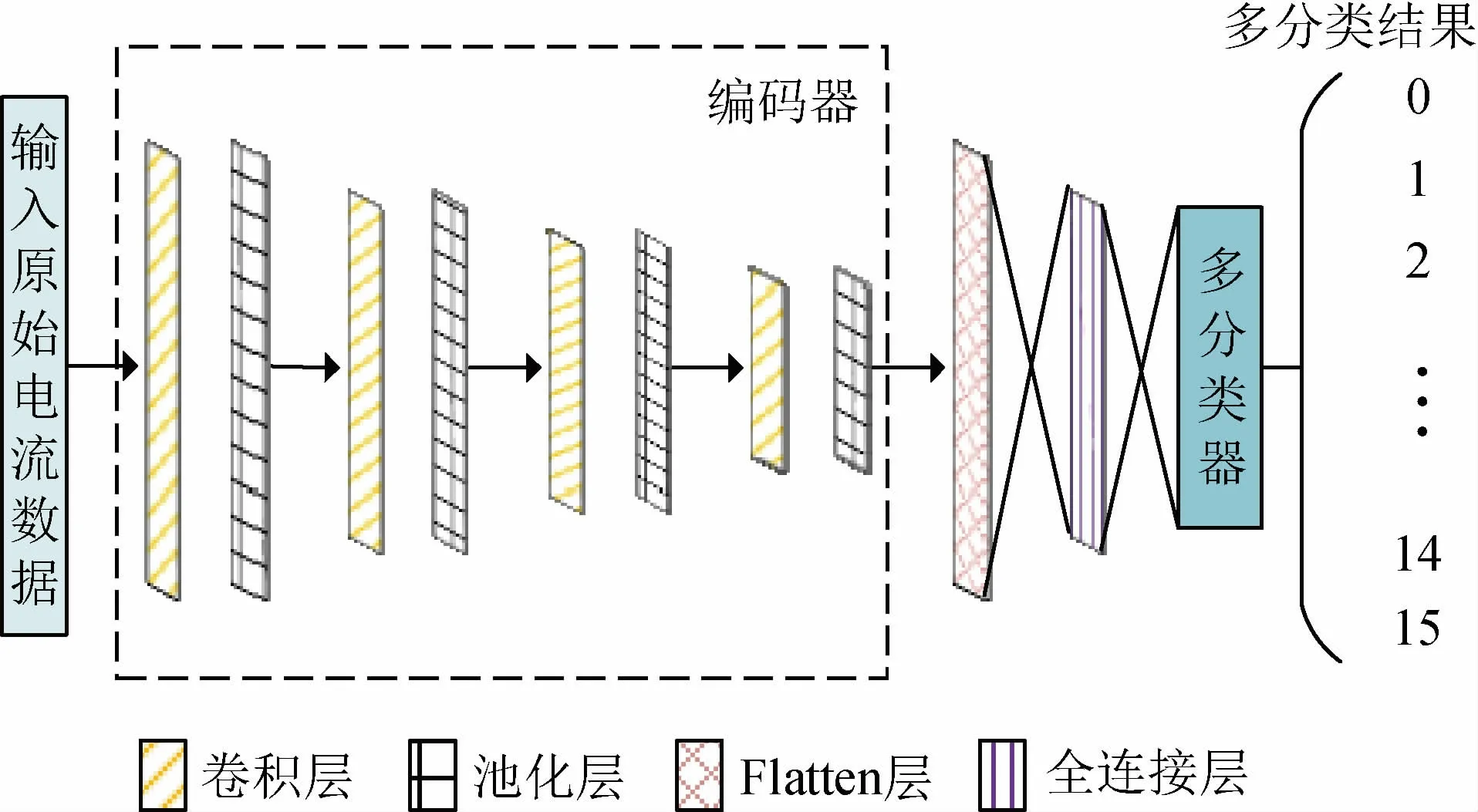
图10 故障电弧多分类识别模型Fig.10 Multi-class recognition model of arc fault
4 故障电弧多分类识别方法实现与 结果分析
4.1 故障电弧多分类识别过程
基于卷积自编码网络的故障电弧多分类识别流程图如图11所示。网络模型训练包括两个阶段:第一阶段是无监督训练卷积自动编码器,输入无标签的一维原始电弧电流数据集,实验选取合适的卷积核尺寸、首层卷积核数量、池化比例、卷积层数,并训练卷积自动编码器的参数,使其成为优异的特征提取器;第二阶段将编码器输出层铺平后连接一个全连接层,再连接至Softmax多分类器,输入有标签的一维原始电弧电流数据集,微调网络参数,完成整个故障电弧多分类网络的训练,网络训练完成后,保存网络模型参数,并输入测试集数据对训练完成的卷积自编码网络的故障电弧多分类性能进行实验验证。故障电弧多分类网络模型参数设置如表3所示。
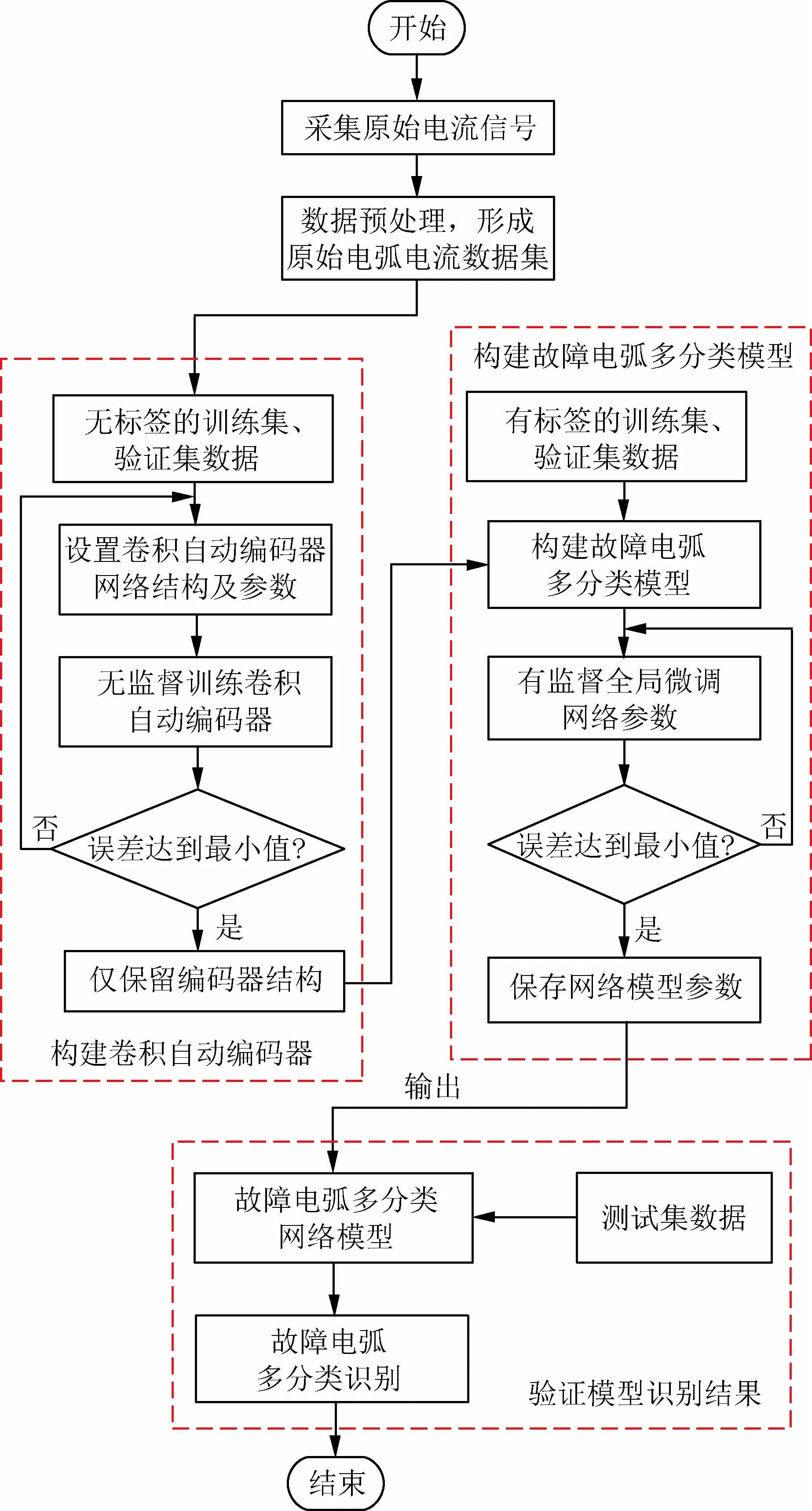
图11 故障电弧多分类识别流程图Fig.11 Flow chart of multi-class identification of arc fault
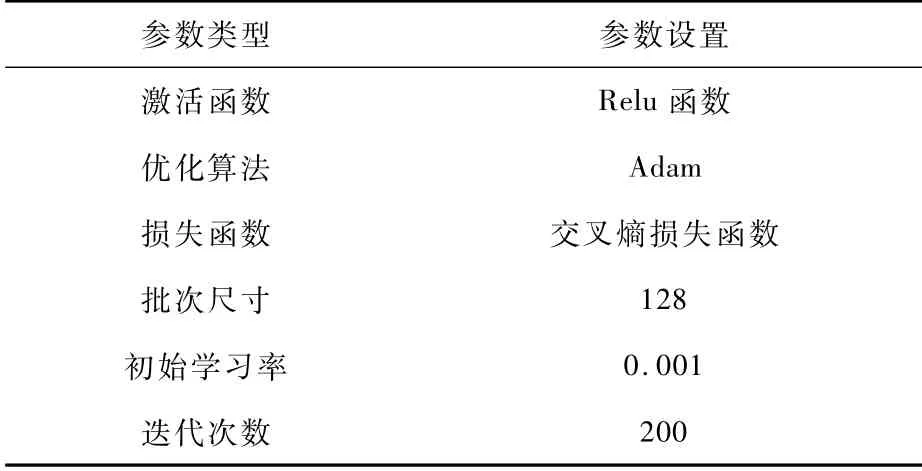
表3 故障电弧多分类识别模型参数设置Tab.3 Parameter settings of arc fault multi-class recognition model
4.2 故障电弧多分类识别结果分析
故障电弧多分类识别模型训练集和验证集的识别准确率如图12所示。由图12可以看出,在迭代过程中,训练集和测试集的识别准确率逐渐上升,训练过程中验证集精度紧跟训练集精度,网络没有发生过拟合。

图12 识别准确率曲线Fig.12 Iterative accuracy curves
取8种负载正常工作与故障电弧状态各100组测试集数据作为模型的输入样本,输入至训练好的故障电弧多分类识别网络模型中,网络输出多分类混淆矩阵如图13所示。其中纵轴label的标签为输入数据的真实标签类别,横轴predict的标签为网络的输出类别标签,对角线数值为分类正确的样本个数,非对角线元素(a,b)为将a样本错判为b样本的样本个数。
由图13可以分析出,故障电弧多分类识别(故障电弧及负载类型均正确识别)准确率为97.94%,负载种类识别正确的概率为98.31%,故障电弧检测的准确率为99.31%,将正常组识别为故障组(误判)的概率为0.062 5%,将故障组识别为正常组(拒判)的概率为0.625%。大多数分类错误样本都是将电阻类电弧样本与其他负载的电弧样本混淆,尤其是与电容启动电机、真空吸尘器负载电弧样本混淆,这是因为电阻类电弧样本的时频域特征与一些非线性负载正常工作时相似,网络模型多分类判据采用的是交叉熵损失函数,输入数据归属于输出值中某一类的条件概率最大的作为分类器输出结果,当不同类样本特征值相近时,条件概率最大的输出值可能误判为其他相似类别,导致分类错误。故障电弧多分类识别模型存在一定程度的误判和拒判情况,但整体而言,在避免人为提取特征量的基础上,故障电弧多分类识别模型能够通过卷积自动编码器学习到有效特征,多分类识别准确率较高。统计各负载的识别结果,如表4所示。
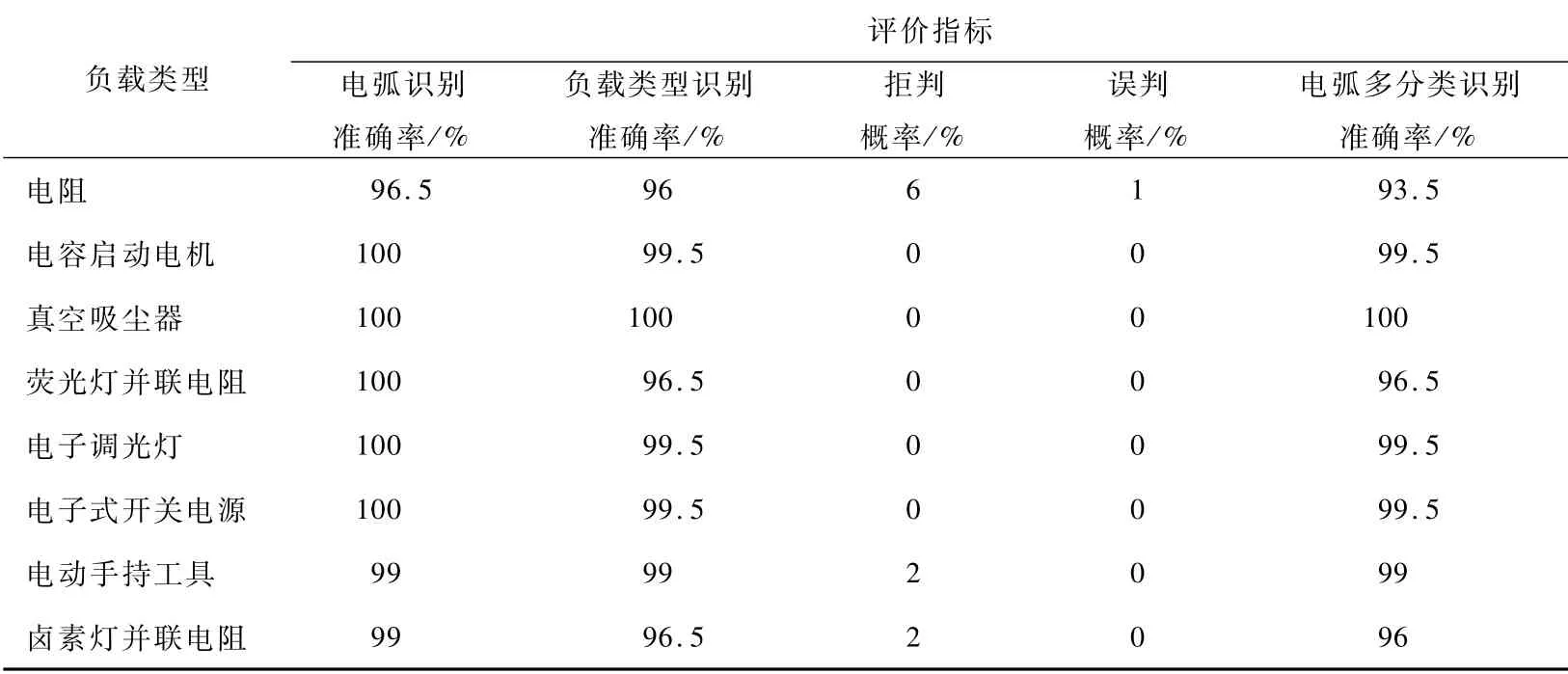
表4 各负载识别结果Tab.4 Recognition results of each load
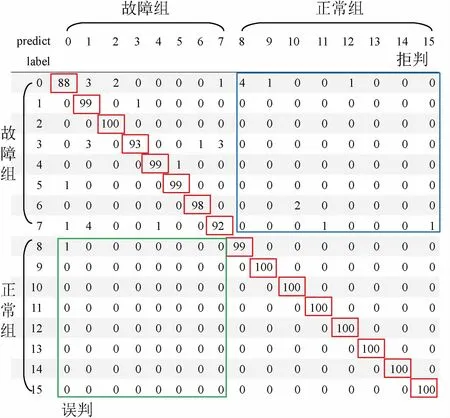
图13 多分类混淆矩阵Fig.13 Multi-class confusion matrix
5 结 论
(1)参照GB/T 31143-2014搭建故障电弧实验平台。采集了不同负载在正常工作与发生故障电弧时的电流数据,并建立了数据集。
(2)提出一种卷积自编码网络模型进行故障电弧多分类识别,该模型能从电弧电流数据中自主提取合适特征,无需人为提取特征量,能够同时进行故障电弧检测与负载类型辨识。
(3)实验验证故障电弧多分类识别的准确率,结果表明,所提网络对不同负载的电弧识别准确率较高,均在96.5%以上,电弧多分类识别准确率均在93.5%以上,能够满足故障电弧识别的准确率要求。
