基于差分隐私度序列的Thurstone模型中参数估计量的渐近性理论

胡军浩，马晓慧，罗敬

（中南民族大学 数学与统计学学院，武汉430074）

随着互联网技术的飞速发展，各种网络平台收集了大量的用户信息.例如，网络购物平台，网络交流平台，医疗就诊信息平台等.这些网络平台的数据有助于分析个人的消费行为、购买偏好以及过往疾病的有效诊断，能够有效解决人们在生活中面临的问题.但是，网络数据在为生活提供便利的同时，也带来了隐私泄露的风险.网络数据通常包含个人及其关联的敏感信息（例如，性关系、电子邮件交换）.如果网络数据在公开前不进行任何的保密处理，那么这些敏感信息很容易受到攻击.因此为了保护网络数据所包含的隐私信息，通常情况下先将网络数据转化成图结构，然后利用图中的度序列研究网络中可能携带的个人隐私信息［1］.因此，在研究网络图模型的过程中，网络节点的度序列的保护至关重要.近年来，在研究网络数据的隐私保护方法中，差分隐私方法受到了极大关注.由于差分隐私是一种隐私标准，限制对一个人的数据进行更改不会显著影响随机数据发布机制中的输出分布［2］，故被广泛用于发布网络数据.

基于此，本文利用Thurstone 模型［3］研究成对比较网络数据的相关统计性质.目前文献［4］利用原始网络数据节点的度序列信息证明了Thurstone 模型下参数矩估计的相合性与渐近正态性.但考虑到网络数据节点度序列的隐私保护问题，本文在文献［4］的基础上研究具有差分隐私度序列的Thurstone模型矩估计问题.本文主要采用文献［5］提出的方法.具体地，首先在Thurstone 网络图模型中利用差分隐私度序列替换原始度序列，然后利用矩方程估计度参数，最后证明矩估计量的渐近性质.据作者所知，基于差分隐私度序列研究Thurstone 模型中参数估计的渐近性质目前较少.因此，在Thurstone 模型下基于差分隐私度序列研究参数估计的统计性质具有重要的实际意义和理论价值.

1 基础知识

1.1 Thurstone网络图模型

成对比较数据通常可用一个有向加权图Gn表示，其中每个节点表示一个个体，从节点i到节点j的加权有向边表示个体i优先于个体j的次数.现考虑具有n+ 1 个节点的有向加权图Gn，节点标记为0，1，…，n.设A=(aij)(n+1)×(n+1)为Gn的邻接矩阵，邻接矩阵A的元素aij表示节点i在tij比较总数中优于节点j的次数，其中tij∈[1，T]表示i与j比较的次数，T为正常数.为了便于说明，令T=tij=tji=aij+aji(i≠j)，并设定aii=tii= 0.记aij(0 ≤i＜j≤n)为服从二项分布的随机变量，即aij~Binomial(T；pij)，其中定义为节点i的度，(d0，d1，…，dn)为网络图Gn的度序列.

Thurstone 模型是研究成对比较数据的模型之一.在该模型下，个体i优于个体j的随机变量aij满足以下概率分布：

其中θi表示个体i的能力水平参数.根据文献［5］的分析，为了保证解的可识别性，设θ0= 0.

故 待 估 参 数θ=(θ1，…，θn)，其中θ∈Rn，R为实数.

1.2 差分隐私

差分隐私是基于临近数据集概念定义的.设两个数据集D1和D2具有相同的属性结构，两者的对称差记为D1ΔD2，|D1ΔD2|表示D1ΔD2中记录的数量.若|D1ΔD2| = 1，则称D2和D1为临近数据集.下面给出差分隐私严格的数学定义：

定义1［6］设有随机算法A，PA为算法A所有可能的输出构成的集合.对于任意两个临近数据集D2和D1（相差一条记录）以及PA的任何子集SA，若算法A满足：

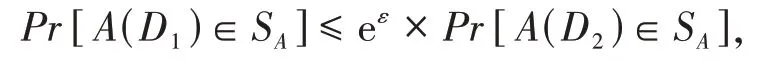
则算法A提供ε—差分隐私保护，其中隐私参数ε＞0.

隐私参数ε由管理隐私政策的数据管理员选择，控制着隐私和效用之间的平衡.ε越小表示隐私保护水平越高［6］.在现有的研究中，图结构一般采取两种常用的差分隐私保护标准，分别为节点差分隐私和边差分隐私［7］.参考文献［7］，本文使用边差分隐私进行研究.边差分隐私的定义如下：

定义2［8］设D1和D2是任意两个只有一条边不同的相邻图，取ε＞0为隐私参数.如果算法A满足：

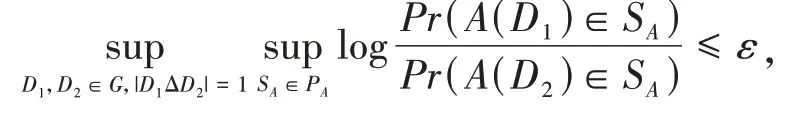
则称算法A满足ε—边差分隐私.其中G是n个节点上感兴趣的所有有向图的集合.

一般情况下，实现边差分隐私是利用Laplace机制（数值型）和指数机制（离散型）的噪声对数据进行加噪，从而实现数据的隐私保护.由于两种机制都依靠全局敏感度，故先给出全局敏感度的定义.

定义3［8］（全局敏感度） 给定查询函数f：G→Rk，G为输入数据集，Rk为输出数据集.在任意一对临近数据集D1和D2上，函数f的全局敏感度定义为：

其中‖f(D1)-f(D2)‖1是f(D1)和f(D2)间的一阶距离.全局敏感度度量了当输入数据集变化时，对相应输出结果的影响.

本文考虑利用Laplace机制实现边差分隐私.由文献［8］中的结论可知，当f(G)为整数时，可以使用一个离散的Laplace随机变量作为随机扰动，并且随机扰动服从以下分布：

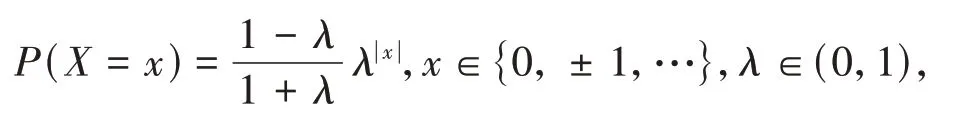
其中x= -Δ(f)logλ.下面给出关于Laplace 机制的相关敏感度定义.

定义4［8］给定查询函数f：G→Rk.e1，…，ek相互独立，且服从参数为λ的离散Laplace 分布.离散Laplace 机制的输出f(D1)+(e1，…，ek)满足ε—边缘差分隐私，其中ε= -Δ(f)logλ，并且：

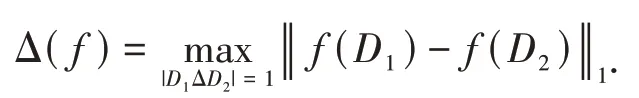
1.3 相关引理

引 理 1［4］设A=(aij)(n+1)×(n+1)，aij~Binomial(T；pij)，其 中TΦ(||θ*||∞)[1 - Φ(||θ*||∞)]，θ*∈Rn为 参 数 真 值.若则当n→∞时，S{d-E(d)}的前k个元素组成的向量服从均值为0、协方差矩阵为B=(bij)k×k的渐近正态分布，这里：

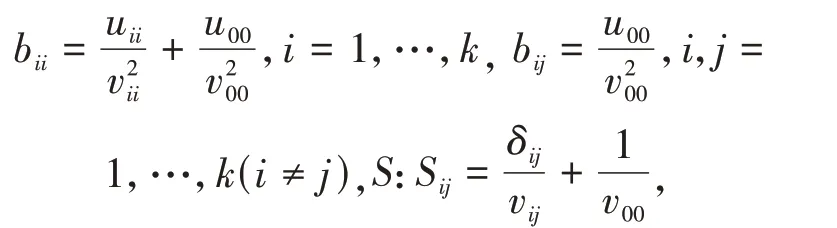
引 理2［9］若 矩 阵V=(vij) 满 足vij=vji，vij＜且V的 近 似逆矩阵为为Kronecker delta 函数，则：

其 中

引 理3［10］F：D⊆X→Y为Fréchet 可 微.若x0∈D时，F"(x0)可逆，且满足：

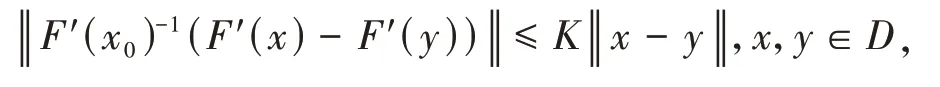
则有：（1）牛顿迭代公式xn+1=xn-F"(xn)F(xn)中的xn(n≥0) 在中，并 且xn(n≥0) 收 敛 于F(x0)= 0的解x*；

2 主要结果及证明

首先考虑度序列包含着网络数据节点的隐私信息.由定义4，设f：Gn→d，Δ(f) = 2.定义为服从参数λ的离散Laplace 分布，则添加噪声后的输出结果满足ε—边差分隐私.本文主要在差分隐私度序列基础上，利用矩估计方程估计度参数.为了得到参数估计的渐近性质，需定义以下函数：

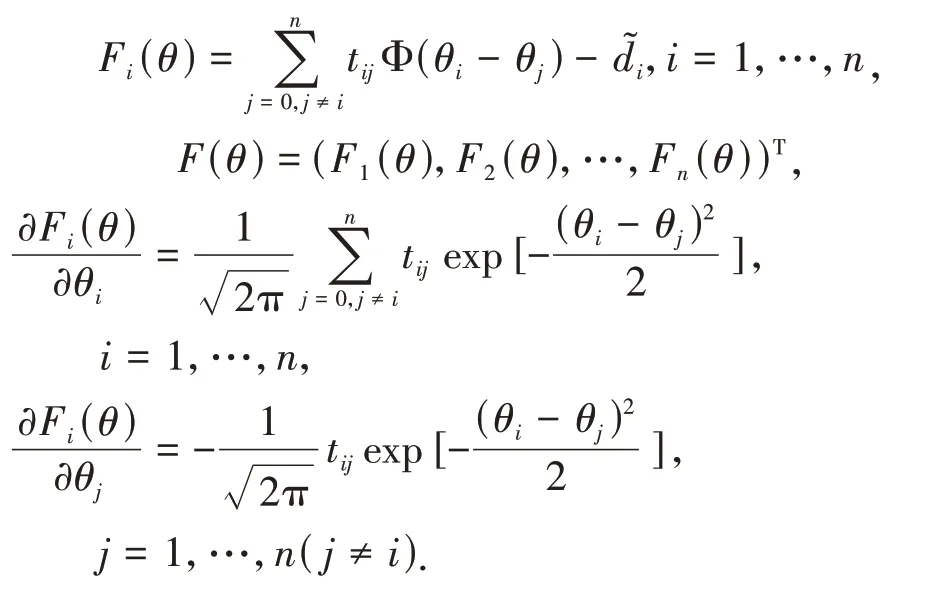
记V=(vij)：=F"(θ)，根据函数的单调性可知：结 合 引 理2 结 论 可 知：m=的近似逆S：

定 理 1设A=(aij)(n+1)×(n+1)，aij~Binomial(T；pij)，其 中若ε(1 +(nlogn)1/2)≥4logn，且τ＜1/12，则n→∞时，参数θ*的估计值存在且：

证明

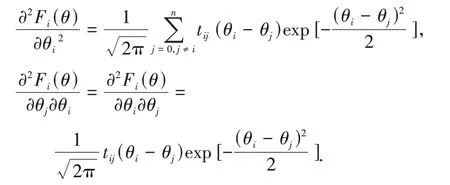
由函数xexp(-x2/2)的单调性可知，结合向量值函数的平均值定理［11］：

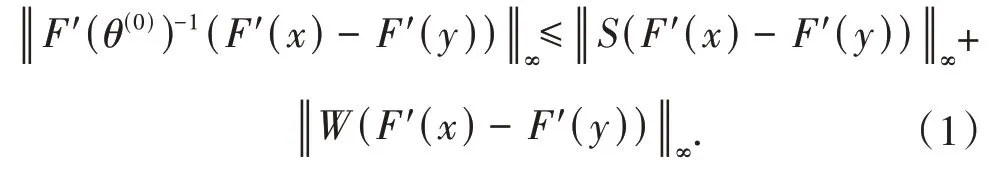
下面分别证明（1）式中的两部分：

随着媒体融合时代的到来，新闻编辑要想更好地适应这一新环境下的要求，就必须对这一时代下的新闻编辑素养重新进行思考。

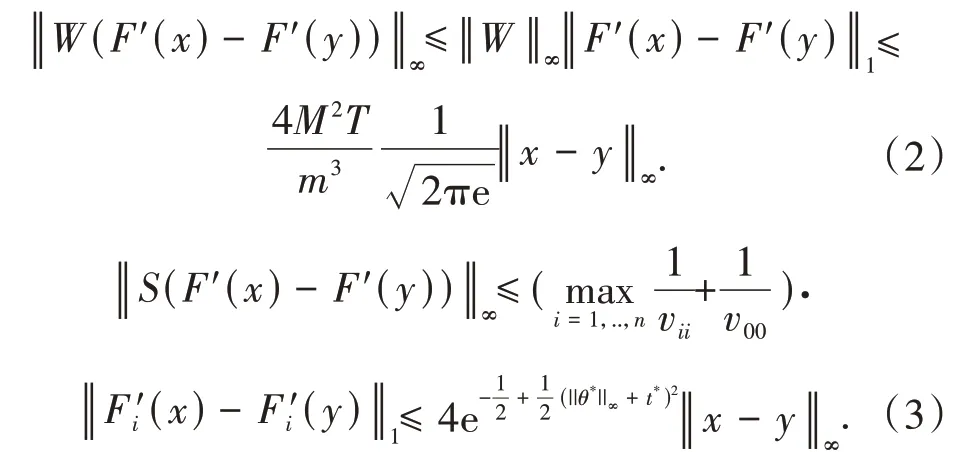
故：

下 面 继 续 计 算η，||F"(θ(0))-1F(θ(0))||∞≤||SF(θ(0))||∞+||WF(θ(0))||∞，

当i= 1，…，n时，通过泰勒展式得到：

若e3(||θ*||∞)2=ο(n1/2)，根据切比雪夫不等式可知：

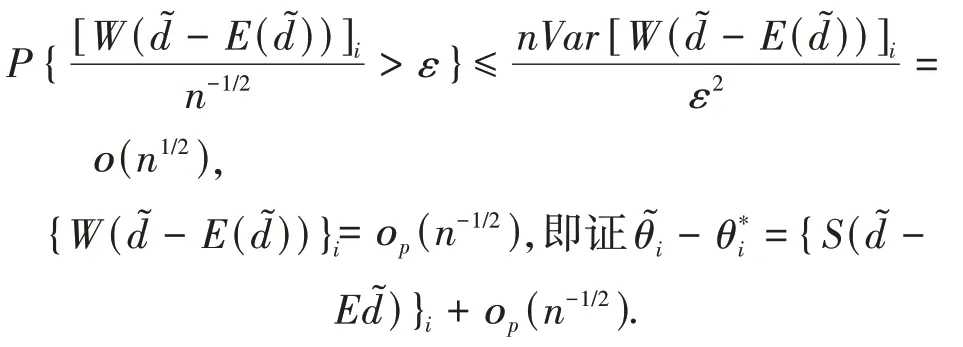
结合引理1和切比雪夫不等式：

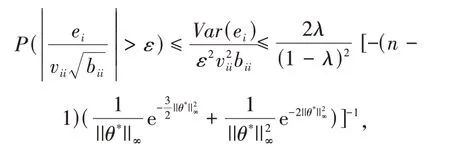
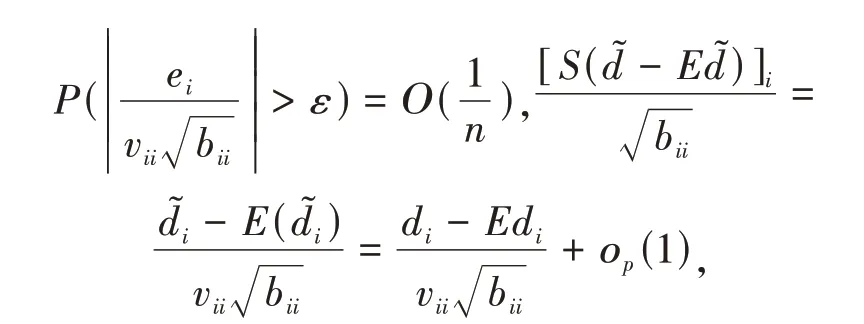
3 数值模拟

在本节中，通过数值模拟验证得到的理论结果.首先参考文献［4］的模拟研究，设参数=iL/n，i=0，1，…，n.针对n= 100，200两种情况，考虑L的4个值，分别为0、0.2*logn、0.5*logn、0.8*logn.基于上述参数设定，本文模拟了3 个不同的ε，分别为2、log(n)/n1/4、log(n)/n1/2.为了验证定理2 中的渐近性质，取是bii中θ*替换为后的值；然后使用QQ图评估ξij的渐近正态性；最后给出了θ*i-θ*j的95%置信区间，-的覆盖率和置信区间的长度以及矩估计不存在的概率为0.

根据图1 可以观察到，ε= 2 时经验分位数与标准正态性分位数吻合很好.

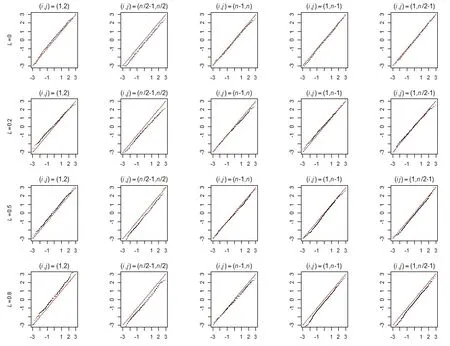
图1 QQ图（ε=2，t=100）Fig.1 The QQ plot（ε=2，t=100）

根据表1观察到，与预期的一样，置信区间的长度随着L的增加而增加，随着t的增加而减少.当ε=2 时，大多数估计的模拟覆盖率接近目标水平.ε= log(t)/t1/4的结果也表现出类似的现象；而ε=log(t)/t1/2时，模拟结果明显低于目标水平.

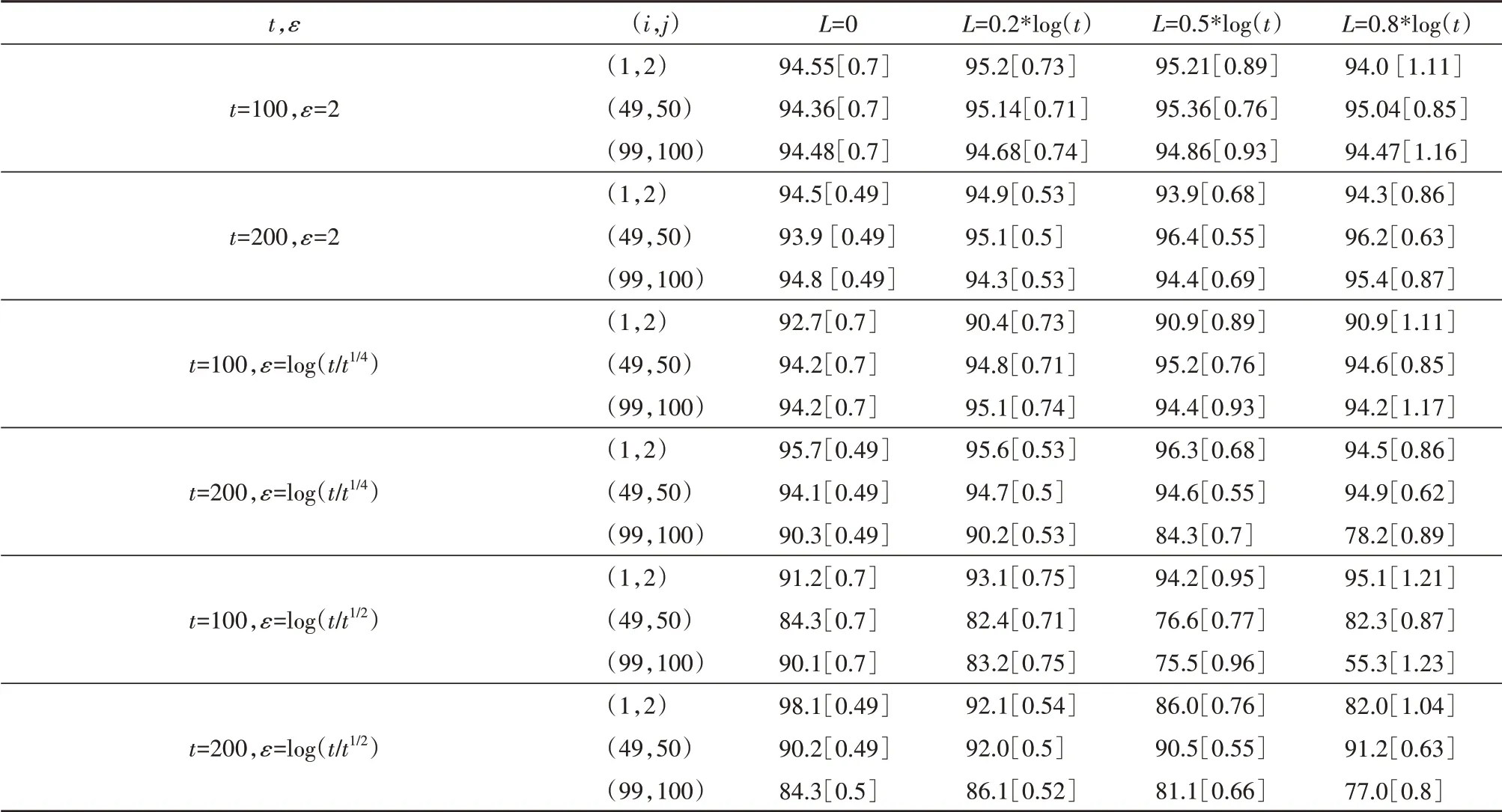
表1 （θi*-θj*）对（i，j）的覆盖率与置信区间长度Tab.1 Estimated coverage probabilities of（θi*-θj*）for pair（i，j）as well as the length of confidence intervals

4 结论

（1）在忽略加噪过程的情况下，利用差分隐私度序列=di+ei替换度序列di得到矩估计方程，进一步利用矩估计方程证明了基于差分隐私度序列参数的矩估计量的相合性与渐近正态性；

（2）结合数值模拟进一步说明理论结果，结果表明差分隐私度序列可以直接用于统计推断；

（3）本文研究的成对比较是稠密的，而在许多应用中，成对比较可能是稀疏的［12］.如何分析当实验个体数量趋于无穷大且成对比较稀疏时模型的渐近性质，值得探索和研究.从数值模拟结果中还可以看出，对||θ*||∞的限制条件可能是宽松的，以后将继续研究这个问题.