基于模态法的形变重构技术应用研究*

戴苏亚，丁 可

（南京电子技术研究所，江苏 南京 210039）

引 言

相控阵天线作为雷达的核心，直接决定了雷达探测能力的强弱。随着技术的不断进步和作战需求的提升，相控阵天线正逐渐向大口径、轻薄化方向发展。然而，大口径、轻薄化天线给相控阵雷达的服役保障带来巨大问题。相控阵天线包含成百上千个天线单元，通过改变每个天线单元的相位实现波束扫描，其电性能与阵元位置精度及反射面的面精度高度耦合。轻薄化会导致天线刚度不够，在环境载荷如振动、冲击、自重、太阳辐照、雨雪、风载等因素的影响下，阵面结构会产生较大应变。天线口径越大，结构应变累积造成的阵元位移偏差会越严重，进而影响天线的指向精度、增益、副瓣等性能指标，降低雷达探测能力。

因此，未来先进的相控阵雷达天线结构必须放弃以“抗”和“防”为主的传统刚度设计方法，采用主动控制技术，实现相控阵雷达对结构形变的感知与补偿，才能同时满足各项作战需求。传统的光学测量方法无法将传感器与阵面高度集成，也无法实现实时测量。基于模态法的天线阵面重构技术通过少量传感器测量天线的实时变形，反馈给雷达进行补偿，从而提升天线的指向精度、增益等性能。

形变重构的各种方法中，文献[1–2]提出了逆有限元法，基于最小二乘变分对板壳结构进行位移重构；文献[3–4]基于模态理论推导出应变–位移转换关系，利用转换矩阵求解目标位移值；文献[5–6]提出了一种建立在经典梁理论上的位移理论，适用于桁架结构；文献[7]提出了基于曲率值对结构表面位移场进行重构的算法。其中，模态法重构相比其他3种方法有较好的稳定性、计算速度和适应性，同时该重构方法对传感器的布置位置要求也较低。考虑到有源相控阵雷达反射面传感器布置的位置局限性大，对变形响应时间的要求高，因此，模态法更适用于相控阵雷达反射面的形变重构场景。

本文首先阐述了模态法重构的基本理论，然后通过有限元软件提取某相控阵雷达实验平台的模态位移矩阵和模态应变矩阵，最后在该平台上进行了重构实验，对重构结果进行了分析评估。

1 模态法重构基本理论

对于多自由度线弹性阻尼系统[8]，其节点坐标系下的动力学模型可以表示为：

式中：εij为第i个自由度的第j阶模态应变；M为传感器数目；e(t)为测试噪声；d为传感器的布置位置；ΨM(d)为模态应变矩阵中布局应变传感器位置对应的行所组成的子矩阵。

由式（2）和式（7）可知，只要准确求出模态坐标qm(t)，就可以建立应变到位移的转换关系。

当阵面结构上布置的应变传感器数目大于等于截断模态数目时，qm(t)可通过最小二乘法求得：

式中，Φs为感兴趣位置所对应的模态位移矩阵。因此，通过转换矩阵T(d)，可由少量应变测点数据推出感兴趣自由度的形变数据。

2 实验平台建模

为验证本文方法的适用性和可行性，以某相控阵雷达实验平台为对象进行实验验证和分析评估。如图1所示，实验平台由骨架、面板和8个单元模拟件组成。8个单元模拟件与面板通过螺钉连接。骨架与面板通过9个作动器连接，用于产生垂直于面板方向的位移，如图2所示。9个作动器组合作用产生模拟变形，模拟各种变形工况。光纤光栅传感器布置在面板表面，用于测量面板表面的应变值。8个单元模拟件用于模拟天线单元反射面，在反射面上粘贴光学测量靶标，用于测量反射面的实际位移值。

图1 实验平台组成示意图

图2 作动器调整装置

由于测试系统模型复杂，整体有限元分析难度较大，因此，针对面板和单元模拟件进行有限元分析，将骨架和作动器作为外部约束进行考虑。利用ANSYS Workbench软件建立有限元仿真模型，如图3所示。

图3 实验对象有限元模型

通过有限元软件对实验对象进行模态分析。本文提取了测试对象的前8阶模态，见表1和图4。分别提取测试点的各阶模态应变与目标点的各阶模态位移。

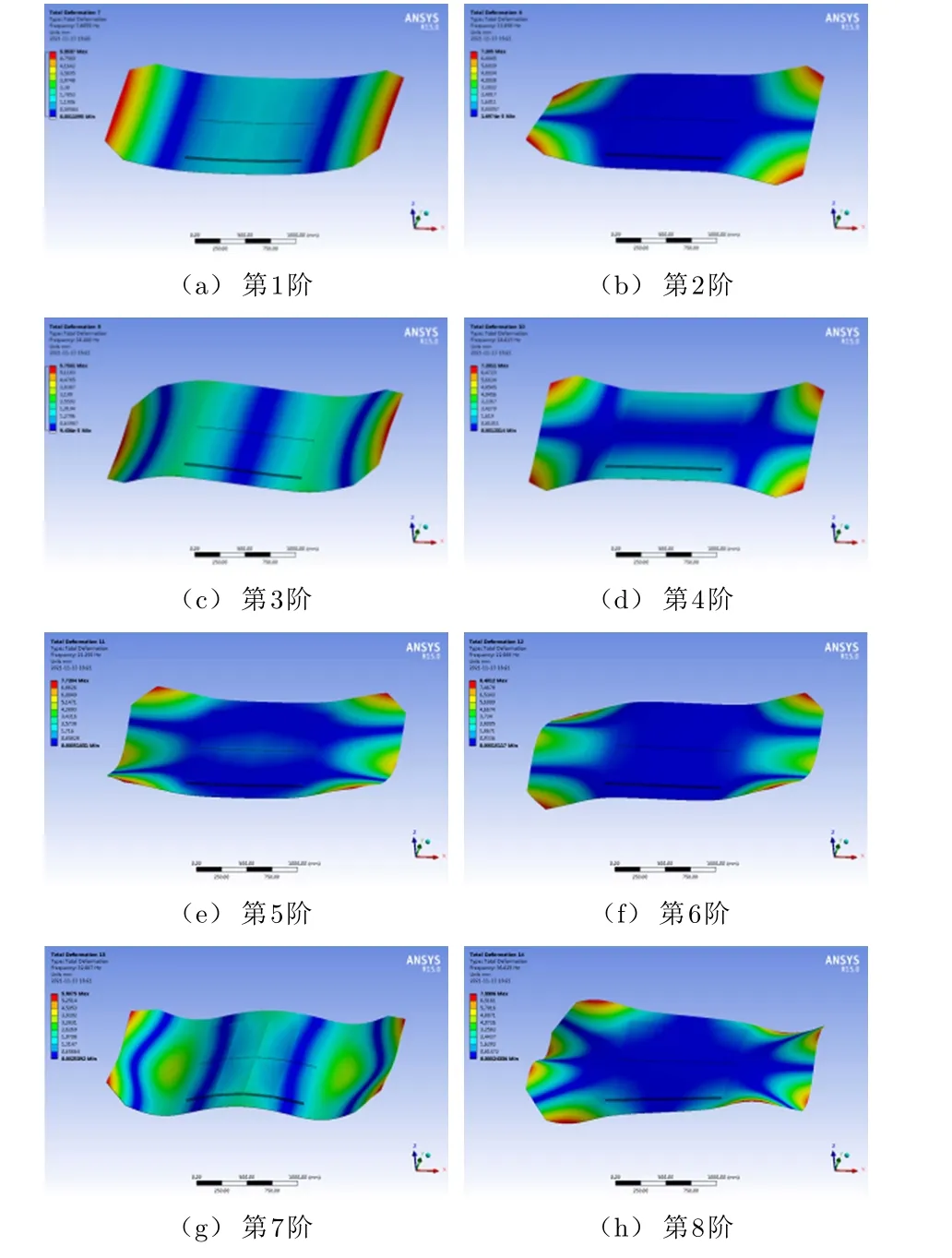
图4 实验平台前8阶振型

表1 实验平台前8阶固有频率 Hz

通过对面板上的传感器测试点提取各阶模态下的应变值，得到模态应变矩阵Ψ。通过对目标点提取各阶模态下的位移值，得到模态位移矩阵Φ。根据式（9）实现测点应变值到目标点位移值的转换计算。

3 重构方法实验验证

骨架与面板通过9个作动器的组合作用产生模拟变形，读取面板表面应变值，重构出反射面形貌。在8个单元模拟件表面粘贴光学测量靶标，测量调整机构作用下目标点的实际位移。将重构值与实际位移值进行比对，评估本文采用的重构方法的可行性。

实验平台的应变传感器布局如图5所示，平台上一共布置了4串光纤光栅传感器，共有28个横向（X向）应变传感器和6个竖向（Y向）应变传感器。重构点为256个靶标点，均匀地布置在8个单元模拟件上。

图5 传感器布局

本文进行了两种工况的重构实验。工况1：左右两端6个作动器固定，中部3个作动器同时运动，做相等的位移，实验结果见图6。工况2：四周8个作动器固定，中部1个作动器产生位移，实验结果见图7。两种工况下的重构误差统计见表2。

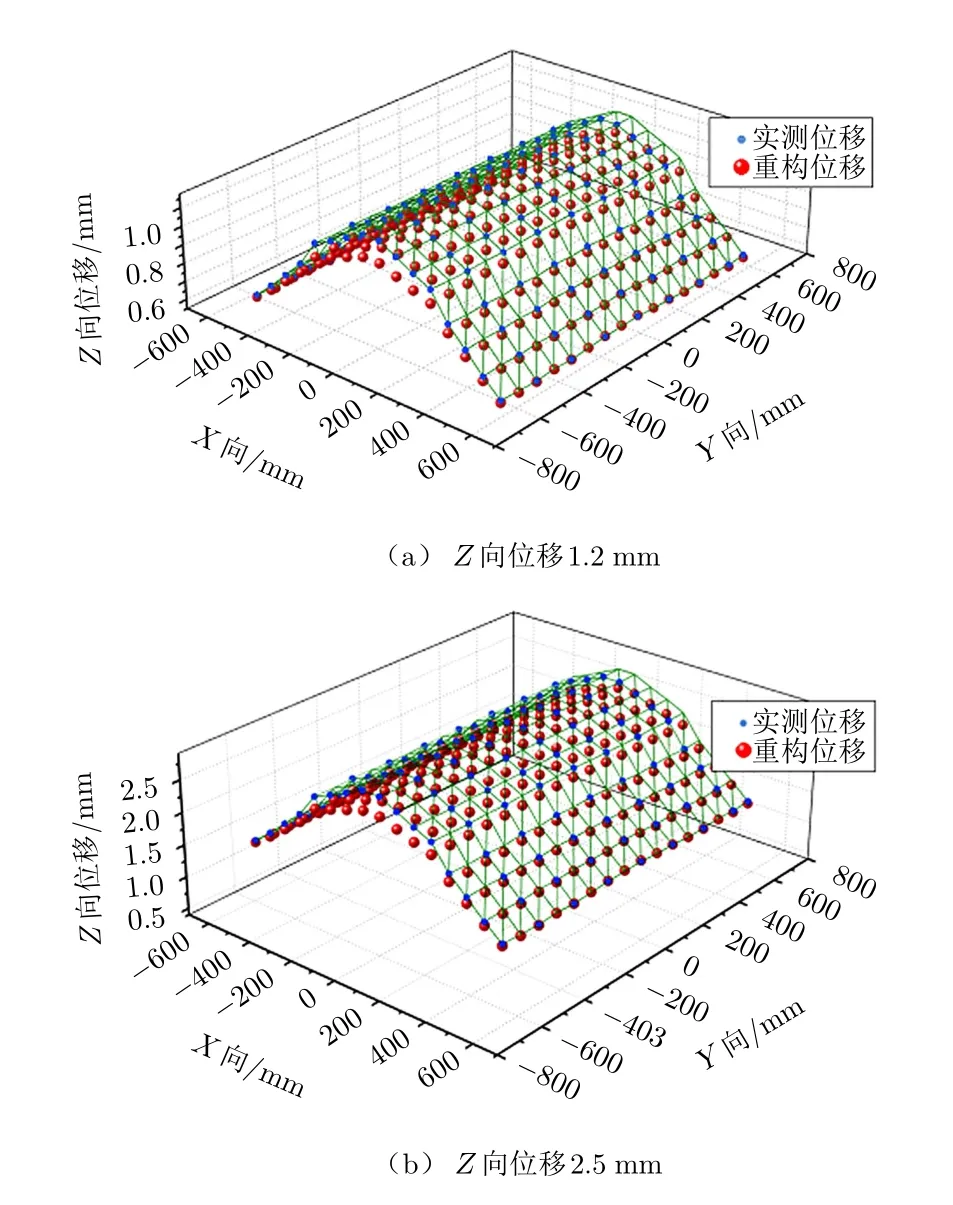
图6 工况1重构结果对比

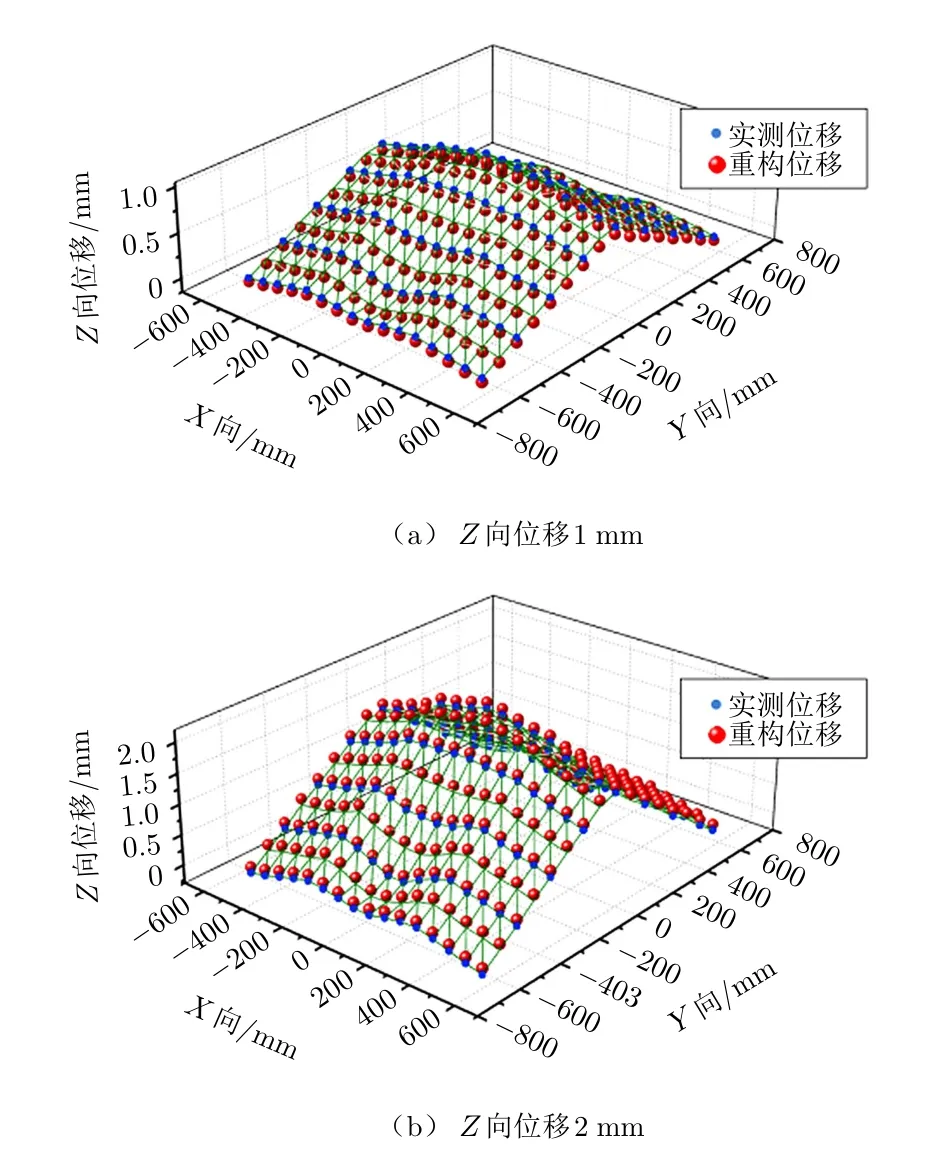
图7 工况2重构结果对比

表2 两种工况下的重构误差统计

由工况1与工况2重构结果的对比可见，工况1下的重构精度要稍高于工况2，主要是因为工况1的约束工况更易于仿真分析，所以工况1下的约束模态更加准确，从而重构结果更加准确。模态法的主要误差来源于仿真模型的构造和应变测试误差。误差主要存在于：1）模态法需要从有限元模型中提取模态位移矩阵和模态应变矩阵，而仿真模型并不能完全等效于被测对象。在此实验平台的仿真中，单元模拟件的结构形式做了简化，同时，从网格的划分设计到被测模块的分割与离散都会导致分析中出现误差。2）模态法的输入是测点的应变输入，测点的位置、数量和方向是否有效合理都会对精度产生影响。3）模态法基于应变–位移转换矩阵，需要合理选取截断模态，同时分配各阶模态权重，该处理也会产生计算误差。综上所述，通过提升仿真模型精细程度、优化传感器布局、合理选取截断模态等可以进一步提升重构精度。

实验结果表明，模态法重构能够很好地拟合出反射面的形貌特征，较为接近反射面的实际变形，可以作为天线阵面实时形变重构的方法。

4 结束语

本文以某相控阵雷达实验平台为对象，研究了基于模态法的形变重构方法。通过有限元软件计算获得应变–位移转换矩阵，并实验验证了该重构方法的可行性。后续工作将着重于在此基础上提升重构精度，主要方向为增加补偿算法，降低测试误差带来的影响，同时对更加复杂的天线阵面结构进行理论和实验研究，推动阵面形变重构方法的实际应用，提升雷达性能。