地铁钢弹簧浮置板高频失效影响分析

倪 昊，张宏亮，申琼玉，初 强，曾向荣

[1. 安境迩(上海)科技有限公司，上海 200137；2. 北京城建设计发展集团股份有限公司，北京 100037]

钢弹簧浮置板已成为我国地铁振动控制要求严苛地段几乎唯一的减振措施，在全国已开通的各城市地铁线路中，钢弹簧浮置板的铺设总长已达到数百公里。

钢弹簧浮置板减振效果好，但系统零部件多，结构和施工工序复杂，施工质量不易保证，因此容易出现减振效果达不到期望值或留下病害的情况。综上，为确保钢弹簧浮置板的安全可靠性及减振效果，应尽量使其结构简单，方便施工安装与维护。

在钢弹簧隔振技术领域，存在钢弹簧高频失效影响减振效果的说法，但并未见到有关地铁钢弹簧浮置板高频失效原因、频率范围及对浮置板减振效果的实质影响的研究成果及测试数据，仅在部分文献中有所提及，选取一些相关文献如下：

(1) 《环境噪声与振动控制工程技术导则》(HJ 2034—2013)[1]的编制说明：弹簧高频时逐渐成刚性，弹性变差，隔振效果变差，被称为高频失效。

(2) 部分城市地铁建设部门编制的弹簧浮置板轨道技术标准早期版本[2]要求：固体传声试验中，隔振器在设计静载荷和高频激励作用下，在50～400 Hz范围内的传递损失不应低于30 dB，弹簧固有频率附近的传递损失塌陷不应大于20 dB，这实际上也是针对钢弹簧高频失效问题所做的规定。

(3) 专利“控制阻尼弹簧浮置道床隔振器高频失效的弹性底座”[3]描述：当激励频率大于弹簧隔振器30倍自振频率以上时，高频激励振动将沿隔振器弹簧丝传递，形成显著的中高频固体噪声传导辐射，导致隔振器的减振降噪性能下降。

钢弹簧浮置板的组成典型断面示意图如图1所示。

一些地铁中应用的钢弹簧浮置板也采取了针对高频失效的技术措施，典型做法是在钢弹簧隔振器底部增设弹性阻尼垫以过滤高阶频率引起的响应，但这也使钢弹簧浮置板的零部件进一步增多，施工安装也更为复杂，因此有必要对钢弹簧浮置板高频失效问题及采取措施的必要性进行专门分析与探讨。

1 钢弹簧高频失效计算分析

在钢弹簧浮置板系统中，浮置板与钢弹簧构成质量-弹簧系统。一般的计算模型中往往仅关注其设计刚度值与质量构成的系统固有频率，而忽略其自身形状、构造及质量。将钢弹簧隔振器简化为抽象的弹簧阻尼单元，算得的钢弹簧浮置板系统荷载传递率与调谐比的关系会比较理想化[4]，理想的钢弹簧浮置板荷载传递率与调谐比关系曲线如图2所示。

然而钢弹簧自身也存在多个固有频率及振型，因此本文建立以下两种对比有限元模型，通过计算质量-弹簧系统的模态参数及力传递率来分析钢弹簧的高频失效问题。

1.1 两种仿真计算模型

由于本文主要研究对象为钢弹簧，为避免浮置板自身弯曲、扭转等高阶模态的干扰，本文建立的两种仿真计算模型将浮置板与钢弹簧隔振器进行简化，采用质量-弹簧系统进行分析，重点对比不同钢弹簧建模方式下的隔振效果差异。

(1) 理想质量-弹簧模型：忽略钢弹簧质量及实际形状的理想单自由度质量-弹簧模型，钢弹簧采用弹簧单元来模拟，其垂向刚度参考实际弹簧模型输入。弹簧底部节点固定，弹簧顶部节点与质量块底部200 mm×200 mm面积的节点建立分布耦合。

(2) 实体单元质量-弹簧模型：考虑钢弹簧质量及实际形状的单自由度质量-弹簧模型，钢弹簧采用实体单元来模拟。钢弹簧底部采用固定约束，刚弹簧上部端面与质量块底部采用绑定处理。

两种模型中的质量块均采用实体单元，质量块质量参考典型的钢弹簧浮置板分配在单个钢弹簧上的质量计算，设为1.2 t。实体单元钢弹簧的典型参数为：高度185 mm、有效圈数2.45圈、弹簧圈直径128 mm、弹簧线径44 mm、垂向刚度7.2 kN/mm。分析采用基于模态的稳态动力学方法，阻尼参数通过在稳态动力学分析中设定Direct Damping(直接阻尼)参数实现。两种单自由度质量-弹簧系统仿真模型如图3所示。

1.2 两种仿真模型算得的固有频率及振型

采用理想质量-弹簧单元仿真模型算得的质量-弹簧系统仅有12 Hz垂向振型。

采用实体单元质量-弹簧仿真模型算得的质量弹簧系统前6阶固有频率及振型如表1所示。

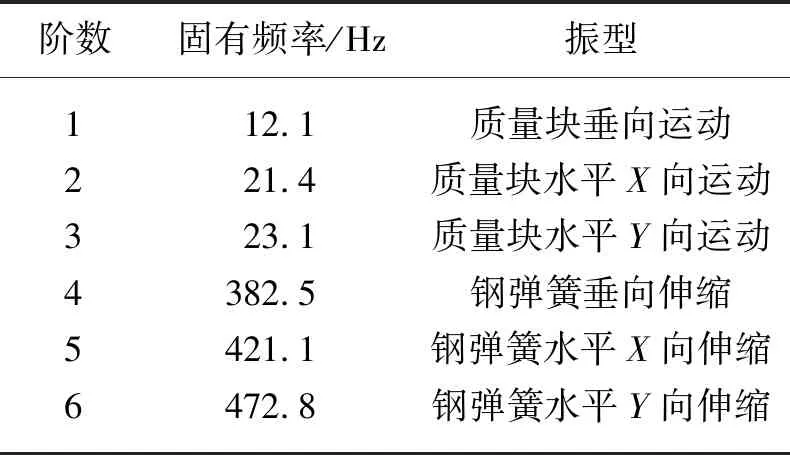
表1 采用实体单元质量-弹簧仿真模型算得的质量-弹簧系统前6阶固有频率及振型

其中前3阶振型固有频率分别为12.1 Hz、21.4 Hz和23.1 Hz，振型主要为垂向及水平向运动；从第4阶开始，固有频率均在380 Hz以上，且均以钢弹簧自身的振型为主。

可见，钢弹簧自身对质量-弹簧系统的振动特性也有贡献，只不过其自振频率相对较高。

1.3 两种仿真模型算得的力传递特性

仿真计算中，为分析钢弹簧的高频失效特性，对质量块施加扫频载荷Finput作为输入，提取钢弹簧底部的支承反力Foutput作为输出，算得不同阻尼比下的力传递率，其计算公式为

(1)

式中，Finput为输入载荷，N；Foutput为输出载荷，N；Tr为传递率，dB。

不同仿真模型钢弹簧固有频率处的传递损失如表2所示，两种仿真模型算得的力传递率曲线如图4所示。由图4可知，采用相同阻尼比参数(5%)的理想质量-弹簧单元模型与实体单元质量-弹簧模型算得的力传递率曲线在≤100 Hz频段基本重叠，都表现为典型的单自由度隔振系统传递率曲线，在该频段范围内，两种计算模型计算所得传递率曲线特性都与图2所示一致。但在≥125 Hz频段，实体单元质量-弹簧模型算得的力传递曲线幅值开始逐步增加，即传递损失降低，钢弹簧固有频率382.5 Hz处的传递损失达到峰值，即出现了传递损失塌陷现象。由计算得到的力传递率曲线可见，阻尼比为1%左右时，钢弹簧固有频率处传递损失会低于30 dB，但阻尼比为5%左右时，传递损失塌陷的程度明显降低，传递损失可满足“50～400 Hz 范围内的传递损失不应低于30 dB，弹簧固有频率附近的传递损失塌陷不应大于20 dB”的要求。

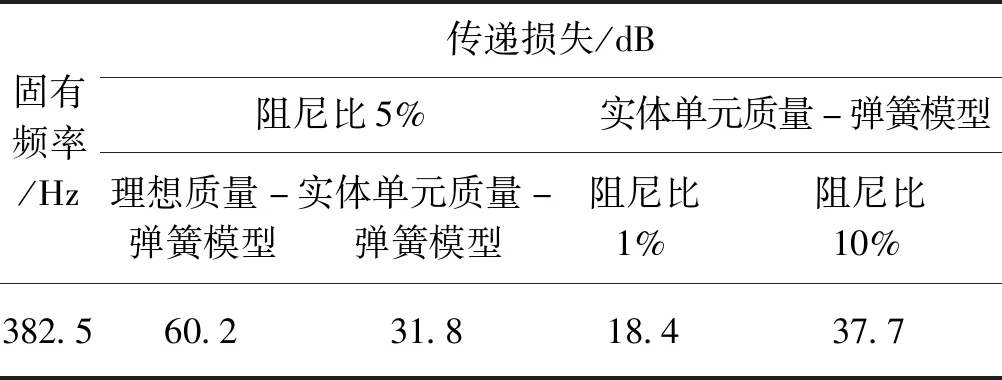
表2 不同仿真模型钢弹簧固有频率处的传递损失

另外，由图4可知，随阻尼的增加峰值传递率会明显降低，阻尼比越高，实体单元质量-弹簧模型算得的钢弹簧共振频段的力传递率越接近理想质量-弹簧模型。

综上，质量-弹簧系统的确存在钢弹簧高频失效现象，为钢弹簧自身局部模态所致。

据《圆柱螺旋弹簧设计计算》(GB/T 23935—2009)[5]，钢弹簧两端固定时的共振频率经验估算公式为

(2)

式中，fe为弹簧共振频率；d为弹簧线径；n为弹簧有效圈数；D为弹簧中径；G为剪切模量；ρ为材料密度。

将前文典型的地铁用钢弹簧参数代入式(2)，可算得其共振频率为

(3)

这与前文实体单元质量-弹簧仿真模型算得的钢弹簧第一阶自振频率382.5 Hz基本一致，验证了仿真模型的准确性。上述经验公式只能算得钢弹簧的第一阶自振频率，无法计算更高阶振型的固有频率。

2 高频失效对钢弹簧浮置板减振效果的实际影响

大量实测统计数据表明，地铁运行引起的振动峰值响应频率基本以40～80 Hz为主[6]，其余频段振动能量相对较小，地铁振动经隧道桥梁结构及沿线土体的衰减后，其中的中高频部分将被进一步吸收，所占分量进一步缩小。典型的地铁振动频谱特性曲线如图5所示。

地铁振动影响及钢弹簧浮置板减振效果评价的主要指标包括以下3个：

(1) Z振级：《城市区域环境振动标准》(GB 10070—88)规定的城市区域环境振动标准值指标，其评价频率范围依据ISO 2631/1确定为0.5～80 Hz[7]。

(2) 建筑物室内振动：其评价的频率范围依据《城市轨道交通引起建筑物振动与二次辐射噪声限值及其测量方法标准》(JGJ/T 170—2009)确定为4～200 Hz[8]。

(3) 建筑物室内二次辐射噪声：其评价的频率范围依据《城市轨道交通引起建筑物振动与二次辐射噪声限值及其测量方法标准》(JGJ/T 170—2009)确定为16～200 Hz[8]。

而地铁典型钢弹簧高频失效频率382.5 Hz远高于上述3个指标的评价频率范围，加之地铁振动传递至敏感建筑的中高频成分很小，故可认为高频失效对钢弹簧浮置板的减振效果并无实际影响，在考虑地铁钢弹簧浮置板设计及减振效果评价时，无须过分关注钢弹簧高频失效的影响。

3 结语

针对某一组典型的地铁钢弹簧浮置板设计参数，采用理想质量-弹簧单元模型与实体单元质量-弹簧模型算得的力传递率曲线在≤100 Hz频段基本重叠，在≥125 Hz频段，实体单元质量-弹簧模型算得的传递损失逐渐降低，在钢弹簧固有频率382.5 Hz处的传递损失降低达到峰值，即出现了高频失效或传递损失塌陷现象，实体单元质量-弹簧模型与经验公式算得的结果相近。

钢弹簧高频失效频率382.5 Hz远高于地铁振动影响及钢弹簧浮置板减振效果评价的主要指标Z振级(0.5～80 Hz)、建筑物室内振动(4～200 Hz)及建筑物室内二次辐射噪声(16～200 Hz)的频率范围，加之地铁振动传递至敏感建筑的中高频成分很小，故高频失效对钢弹簧浮置板系统的隔振效果并无实际影响，即在钢弹簧浮置板的设计中无须过分关注钢弹簧高频失效的问题，亦无须采取防范技术措施，以避免钢弹簧浮置板结构不必要的复杂化。

在需要考虑钢弹簧高频失效的应用中，可通过适当增加钢弹簧隔振器阻尼的方式来抑制高阶频率引起的响应。当系统阻尼比达到10%时，钢弹簧的共振频率处的传递损失塌陷现象已不明显。