后张梁曲线钢束段混凝土局部应力解析

成 晟

(泰州市公路事业发展中心，泰州 225300)

后张预应力混凝土箱梁桥因其整体性好、经济合理、设计和施工技术成熟等优势，在桥梁工程中得到广泛应用。但在桥梁施工和运营阶段，相应梁体可能会出现非荷载型裂缝，从而影响结构耐久性[1-5]。

裂缝分布和波纹管方向一致，主要有3种类型：①大跨径梁或刚构桥的合龙段底板裂缝[1-2]；②悬浇箱梁节段腹板裂缝[3-4]；③曲线梁桥底腹板裂缝[5]。分析裂缝成因，后张预应力梁桥预应力钢束多为曲线布置，不同于直线钢束，曲线钢束张拉时会挤压圆心侧混凝土并拉伸另一侧混凝土，产生局部应力集中，若处理不当会导致底板和腹板等位置裂缝产生并发展。

曲线钢束拉伸时产生的局部集中应力是裂缝形成的直接原因，但目前尚无针对混凝土内局部应力的解析方法。基于拉-压杆模型的现行设计方法未考虑预应力孔道的局部应力状态[2-3]；材料力学和弹性力学分析中梁的受力计算基于圣维南原理，无法计算局部集中应力[6-7]；有限元方法通过单元划分和受力模拟，可对局部应力进行数值计算，是目前最常用的分析工具[2-5]，但其计算精度受网格划分以及单元选择等多种因素影响，不便于工程直接应用。

本研究根据弹性力学的楔形体应力公式，通过应力分解、应力积分和应力合成运算，推导出体内集中力作用下局部应力分布的解析解，在此基础上对大跨径梁合龙段底板、悬浇梁节段腹板以及曲线梁底腹板3种结构在曲线钢束径向压力作用下的局部应力响应及裂缝成因进行分析，得到的应力公式可直接应用于结构受力计算中。

1 钢束径向压力计算

后张法曲线预应力钢束张拉时，由于孔道弯曲，钢束会对圆心方向的混凝土产生挤压，曲线钢束径向压力示意如图1所示。

取任意微段dl研究，径向平衡方程为

2×N×dθ/2=σ×R×dθ×b

(1)

式中，N为钢束拉力，R为孔道曲率半径，dθ为钢束的弯曲角度，σ为混凝土压应力，b为钢束与混凝土的接触面宽度，解此得到

F=σ×b=N/R

(2)

式中，F为单位长度钢束对混凝土的径向压力，方向指向孔道的曲率中心。

2 混凝土局部应力解析

2.1 应力合成分析

钢束对混凝土的径向压力在平面内可作为集中力，研究中只关注钢束与混凝土外表面之间的局部应力，故将混凝土在钢束径向压力下的应力分布近似视为半平面在内部集中力作用下的应力解析，半平面受体内集中力作用示意如图2所示。

弹性力学分析未给出半平面在体内集中力作用下的应力分布公式，本研究将通过应力分解、应力积分和应力合成运算对该问题进行求解，具体思路为：①根据楔形体在楔顶受集中力的密切尔解，计算全平面空间内体系在集中力下的应力分布。②保留有荷载的半平面，移除无荷载的半平面，得到半平面体系。由于在全平面内两个半平面之间的界面上有相互作用，因此移除荷载的同时保留边界应力(含法向应力和切向应力)，以维持受力状态不变。③实际边界为自由表面，不应有任何应力作用，因此添加与边界应力相反的反作用力，以抵消原边界应力，模拟自由表面的应力状态。④利用楔形体为半平面时的密切尔解，通过应力积分运算，得到有荷载的半平面在界面反作用力下的应力响应。⑤将体系在界面反力下的应力与体系在原来全平面内集中力下的应力进行叠加，得到半平面连续体在体内任意集中力作用下的应力状态。

2.2 界面应力分解

楔顶受集中力的楔形体示意如图3所示。

界面应力分解问题的密切尔解为[6]

(3)

式中，楔形体关于x轴对称，α为楔形体的计算角；F为单位长度楔顶集中力数值；ρ为计算点极径；β、φ分别为集中力和计算点相对x轴的旋转角度，以顺时针为正。F与极轴方向一致时取正值，反向时取负值。

全平面受体内集中力作用如图4所示，边界位于y轴上，以荷载作用点在y轴的垂直投影为坐标原点。体系在(h，0)处受集中力F。

取x=0，α=2π，根据密切尔解答式(3)，可得界面上一点M(0，y)处的应力为

(4)

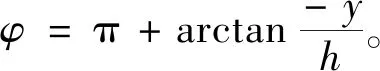
应力分量在极坐标和直角坐标间的变换式为[6]

σx=σρcos2φ+σφsin2φ-2τρφsinφcosφ
σy=σρsin2φ+σφcos2φ+2τρφsinφcosφ
τxy=(σρ-σφ)sinφcosφ+τρφ(cos2φ-sin2φ)

(5)

联立式(3)和式(5)得到

σx=σρcos2φ
σy=σρsin2φ
τxy=σρsinφcosφ

(6)

将式(4)代入式(6)，得到界面上的法向应力和切向应力分别为

(7)

2.3 界面反力效应

因边界为自由界面，实际法向应力和切向应力为0，故添加-σx的法向反力和-τxy的切向反力来平衡全平面的边界应力，界面反向应力示意如图5所示。

设计算点位于N(x0，y0)(0≤x0≤h)，取长度为dy的小段，联立式(3)和式(7)，计算得到(0，y)处法向反力-σx和切向反力-τxy对点N的应力效应为

(8)

联立式(6)和式(8)，转换为对应的直角坐标应力分量为

(9)

其中

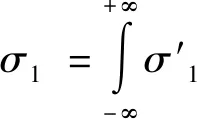
(10)

2.4 应力合成

全平面内集中力F对N(x0，y0)的应力效应可将α=2π代入式(3)计算得到，如式(11)所示。

(11)

将式(11)代入式(6)，转换到直角坐标系，如式(12)所示。

(12)

叠加σ0和σ1可得到N的最终应力状态：式(10)+式(12)得到半平面内任意一点在集中力作用下的应力。

2.5 表面应力分布与边界条件验证

式(10)+式(12)后令x=0，得到集中力作用下半平面边界上的应力分布为

(13)

式(13)满足应力边界条件。

3 混凝土局部应力分析

3.1 竖向集中力

大跨径梁桥和刚构桥的底板纵断面线形一般为抛物线，跨中处曲率最大，底板纵向下弯钢束如图6所示，预应力筋平行于底板布置，进行跨中强度验算时除须考虑底板合龙束径向压力的崩出效应外[1-2]，还应考虑径向压力产生的混凝土横向拉应力，底板竖向集中力如图7所示。

定义混凝土外表面的垂直方向为竖向，平行方向为水平。令F=1 N、h=0.06 m、β=0，考察竖向集中力作用下的水平应力分布，x=0时σy沿y轴分布如图8所示、y=0时σy沿x轴分布如图9所示。

竖向集中力作用下，局部水平应力的最大值出现在集中力在表面的垂直投影点处。

当集中力沿x轴反方向时F<0，σy为拉应力。因混凝土材料不能承受拉应力，且无法在混凝土表面配置钢筋(钢筋保护层)，故此类裂缝难以通过钢筋配置进行防治，应在设计阶段通过结构优化或预应力调整，规避指向混凝土表面的内部荷载。

令x=0、y=0，得到在混凝土表面的水平应力最大值为

(14)

3.2 水平集中力

悬浇箱梁节段纵向下弯钢束张拉后，腹板纵向下弯钢束如图10所示，曲线桥箱梁底腹板纵向平弯钢束张拉后，底板纵向平弯钢束如图11所示，径向压力的产生会使波纹管一侧混凝土受压、另一侧受拉，底腹板横向集中力示意如图12所示。

令F=1 N、h=0.06 m、β=π/2，考察水平集中力作用下的水平应力分布，x=h/2时σy沿y轴分布如图13所示、y=h/2时σy沿x轴分布如图14所示。

水平集中力作用下，局部水平应力沿y轴的衰减较慢，因此进行混凝土补强设计时应适当增大防崩钢筋的设置范围，防止波纹管区域以外的混凝土开裂。

荷载作用点处的水平应力为无穷大，令x=h/2、y=h/2，得到点(h/2，h/2)处的典型水平应力值为

(15)

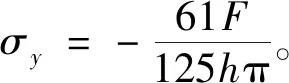
因解析只关注钢束与外表面间的局部应力，故计算中将梁体假设为半平面体系，而实际梁体为有限尺寸空间，得到的应力分布仍与有限元结果吻合[2-4]。

4 结论

针对预应力混凝土中曲线钢束张拉时裂缝成因难以解析的问题，根据弹性力学中楔形体在楔顶受集中力的密切尔解，通过应力分解、应力积分和应力合成运算，推导出半平面在体内集中力作用下的应力响应。在此基础上，对后张梁在竖向和横向曲线预应力钢束张拉时产生的附加应力进行计算，给出最大应力和典型应力的计算公式，并对大跨径梁合龙段底板、悬浇梁节段腹板以及曲线梁底腹板的3种典型裂缝的成因进行分析，可为桥梁设计提供参考。研究发现当曲线钢束产生指向混凝土表面的压应力时，极易导致裂缝发展，应在设计和施工时避免；当曲线钢束平行于混凝土表面时，应增大防崩钢筋设置范围，防止拉应力延伸后引起混凝土开裂。