红外光学微结构表面的高效自适应飞刀切削

李佩铮，杜 雪，孙占文*，王素娟，徐诗俊

（1.广东工业大学精密电子制造技术与装备国家重点实验室，广东广州 510006；2.香港理工大学 工业与系统工程学系 超精密加工技术国家重点实验室，香港 999077）

1 引 言

随着航空航天、生物医学、能源、半导体及电子通信等领域的飞速发展，对红外光学材料的制造与应用的需求也快速增长［1］。硅、锗等红外光学材料因其独特的物理、光学性能得到了广泛的应用。但红外材料的硬脆特性使它在加工时极易产生脆性断裂，鉴于微结构表面的几何特征复杂性，难以在保证效率的同时加工出表面光洁度良好、形状精度严格和表面完整，且不具有亚表面损伤的光学结构［2］。例如，在加工单晶硅材料微结构表面时，塑性加工深度在100～200 nm［3］之间，当采用较大的切削深度和进给速度时，会产生脆性断裂以及延伸至微结构表面的裂纹。为防止裂纹出现，保证微结构的表面质量，须采用较小的进给速度，这会增大加工时间，影响加工效率。尽管采用离子注入改性辅助加工、激光辅助加工等非传统加工方法，能够保证微结构的表面质量与加工效率，但考虑到经济效益，它们仍不是最佳选择。所以，寻找一种红外光学材料微结构表面高效且经济的加工方法仍是一项艰巨的任务。

非机械式加工方法已广泛运用在单晶硅等红外光学材料微结构表面加工中。Wang等在单晶硅片表面多次注入离子，制备较厚的改性层实现材料改性［4］，并通过超精密飞刀切削制备了多条正交圆柱槽组成的塑性微柱阵列。然而，改性层厚度的均匀性难以控制，长时间离子注入降低了加工效率，多次注入离子也增加了经济成本。Chen等研究了激光辅助纳米切割对单晶硅的亚表面损伤和相变，激光辅助增大了单晶硅的脆塑转变临界切深，并以塑性加工的方式在单晶硅上加工了微沟槽［5］，但该方法的加工成本与效率仍达不到最优。这些非机械式加工方法无法满足低成本、高效率的加工需求，而且难以加工出纳米表面粗糙度和亚微米形状精度的微结构表面。

与非机械式加工方法相比，机械式加工方法更加高效经济［6］。该方法不仅可以达到亚微米级的形状精度，在加工红外光学材料微结构表面时还具有更大的灵活性。王紫光等通过超精密磨削技术加工了低损伤表面和高精度面形的单晶硅反射镜［7］。徐领娣等通过精密铣磨加工技术制备了微晶材质自由曲面反射镜，降低了后续研抛加工的材料去除量［8］。罗斌等通过磁流体抛光技术加工出低表面粗糙度的非球柱面镜［9］。Khatri等通过单点金刚石车削加工出用于X光的硅镜，并研究发现刀具进给速度、切削深度和主轴转速对获得良好的硅表面质量起着重要的作用［10］。Tang等通过金刚石车削在硫系玻璃上制备出非球面透镜［11］。为保证红外光学材料高质量微结构表面的塑性加工，在满足微结构表面几何特性的同时，难以保证经济高效。

超精密飞刀切削是一种刀具装夹在主轴上，间歇性切削工件的加工方式［12］。这种加工方式可加工出高自由度且高质量的微结构表面，形状误差可达到亚微米级和表面粗糙度在纳米级［13］。Sun等通过超精密飞刀切削加工Ftheta透镜，验证了在较大进给速度和切削深度下，也可以产生较小厚度的切屑，从而抑制加工中脆性断裂的出现［14］。然而，飞刀切削产生切屑厚度会随着微结构表面的斜率和切削深度的变化而变化。目前，该加工方法的刀具轨迹点是均匀的，并按照所加工的微结构表面产生最大切屑厚度的瞬时位置设定进给速度，忽视了微结构表面其他位置对应的进给速度。所以，自适应超精密飞刀切削红外光学材料微结构表面的方法需要进一步优化。

为进一步提高超精密飞刀切削红外光学材料微结构表面的加工效率，本文通过研究飞刀切削塑性加工模型产生的切屑厚度，来优化动态进给速度，提高加工的平均速度，在保证高质量加工微结构表面的同时提高了效率。通过分析飞刀切削切屑生成的理论模型，计算出自适应飞刀切削刀具轨迹点，确定加工过程中刀具动态回转中心的位置，得到相应的进给速度［15］。最终在单晶硅上加工正弦曲线形微沟槽得到验证，并将加工效率、表面质量和未优化下的参数进行了比较。

2 原 理

2.1 加工原理

为了避免超精密飞刀切削加工过程中红外光学材料发生脆性断裂，最可靠的方法是以塑性方式加工微结构表面。这种方法是通过限制每个刀具旋转周期下产生的最大切屑厚度小于红外光学材料的脆塑转变临界切深来实现。超精密飞刀切削加工不同形貌特征的微结构表面时，每个刀具旋转周期下的最大切屑厚度不仅取决于切削剖面的加工参数（例如进给速度和切削深度），还与切屑位置的局部斜率有关。因此，所加工微结构表面的复杂形貌不可避免地导致切屑厚度随切削位置的改变而变化，从而使加工表面产生脆性断裂，而传统飞刀切削方法加工时难以选择合适的加工参数。目前的解决方法是采用较小的进给速度，这却大大降低了加工效率。针对这一难题，本文提出了一种自适应调速超精密飞刀切削方法，以避免加工中红外光学材料发生脆性断裂。

超精密飞刀切削加工原理如图1所示。金刚石刀具安装在刀架上，刀架固定在主轴上。工件安装在B轴圆盘的夹具上，夹具固定在Z轴轨道上。加工时，首先通过调平机构将工件调至水平，主轴以设定的进给速度沿X轴旋转进给，金刚石刀具间歇性地切削工件。主轴根据加工程序设定运动，生成所需的微沟槽，并按照自适应调速超精密飞刀切削方法计算出的进给速度沿X轴方向进行飞切运动，使微沟槽不同位置处的最大切屑厚度严格小于与其匹配的脆塑转变临界厚度，从而获得均匀无裂纹的微沟槽。

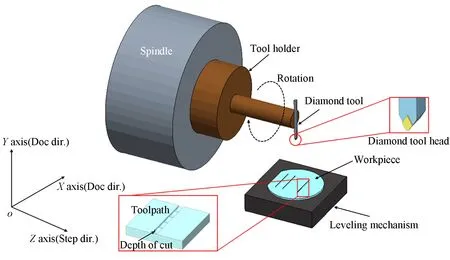
图1 超精密飞刀切削加工示意图Fig.1 Schematic diagram of ultra-precision flying cutting process

优化后的超精密飞刀切削方法具有灵活性高、切削方向恒定等优点。飞刀切削塑性加工模型还具有以下优点：

（1）在加工具有复杂几何形貌特征微沟槽时避免了局部碎裂。在此加工方法中（如图2所示），主动控制沿X轴进给方向的运动，可根据微沟槽的局部斜率与切削深度实时调整瞬时进给速度，从而使每个刀具旋转周期产生的最大厚度是恒定的，切削深度和微沟槽局部斜率的改变对其没有影响。通过主动控制将最大切屑厚度设置为小于脆塑转变临界切深，可有效地避免微沟槽的脆性断裂。而传统飞刀切削的进给速度在加工中不可调节，切屑的最大厚度随瞬时位置变化，这是导致微沟槽加工表面产生脆性断裂且不均匀分布的主要原因。

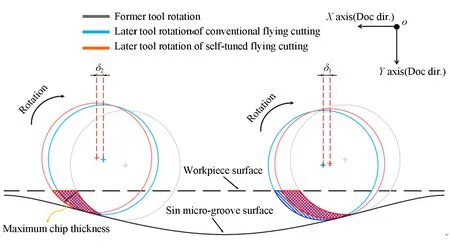
图2 自适应调速超精密飞刀切削和传统超精密飞刀切削的切屑形成示意图Fig.2 Schematic diagram of chip formation of self-tuned ultra-precision flying cutting and conventional ultra-precision flying cutting

（2）提高加工效率。现有的加工方法是采用较小的进给速度，以保证在微沟槽在产生最大切屑厚度处的材料以塑性方式去除，这极大限制了飞刀切削的加工效率。相比之下，自适应调速超精密飞刀切削方法可以在保证不产生脆性断裂的前提下获得更大的平均进给速度，从而极大地提高加工效率。

2.2 飞刀切削塑性加工模型

在自适应调速超精密飞刀切削方法中，刀具沿进给方向的两个相邻旋转周期间歇性切削形成月牙状切屑，微沟槽由于没有步进方向运动，所以产生的切屑为轴对称的，切屑最大厚度分布在切屑的中心平面abc上，如图3（a）所示。最大切屑厚度不仅取决于加工参数，还与切削位置处的瞬时斜率和切削深度有关。加工产生的每片切屑由3个表面组成，分别是原始表面、上表面和下表面，切屑形貌的三维示意图如图3（b）所示。

图3 切屑形貌Fig.3 Chip image

图4为飞刀切削微沟槽切屑生成的数学模型。可以看出，随着刀具旋转，切屑厚度沿进给方向变化。切屑厚度在刀具接触点a处从零增大至b处为最大值，然后逐渐减小，直到在c处减小为零。因此，通过直接计算点b到切屑下表面过回转中心Os交点连线的直线距离，就可以计算出最大切屑厚度。

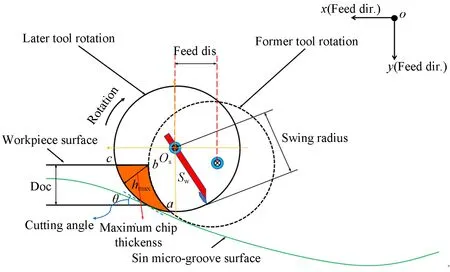
图4 切屑生成的数学模型Fig.4 Mathematical model of chip generation

对于第一刀刀具回转形成的曲线，其边界点包括a和b，其数学表达式为：

式中：fe为进给速度，θ为刀具切削处的沟槽面夹角，Sw为刀具的回转半径，x和y分别为数学模型的横、纵坐标分量。

对于第二刀刀具回转形成的曲线，其边界点包括a和c，其数学表达式为：

未切削原始曲面的边界点包括b和c，可以表示为：

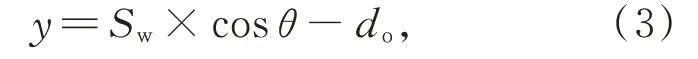
式中do为当前切屑生成时的切削深度。

b为原始表面与第一刀刀具旋转曲线的交点。联立式（1）和式（3）可得b的坐标分量为：

基于方程组（4），可以计算出最大切屑厚度为：

脆塑转变临界切深是红外光学材料以塑性方式和脆性方式去除的阈值。用式（5）中脆塑转变临界切深替换最大切屑厚度hmax，可以最大限度地提高加工效率，并且保证加工出的微沟槽整体光滑，不会出现脆性断裂。

2.3 自适应调速数学模型

传统飞刀切削的刀具轨迹点是均匀分布的，而自适应调速飞刀切削的刀具轨迹点是根据所加工微结构不同位置处的切削深度和斜率计算得出的，所以自适应调速飞刀切削方法的关键是要找到刀具的回转中心Os。在直角坐标系下第二刀的回转中心设为原点Os，通过迭代法依次求出下一转刀具回转中心的位置，以此类推，计算出整个微沟槽加工时刀具回转中心的位置。为了确定刀具回转中心的位置，设进给方向未知量f，切深方向未知量y，将刀具回转轨迹划分为2N个点，用未知量f，y表示。将含有未知量f，y的每一个点带入到微沟槽轨迹方程F，联立式（5）求出：

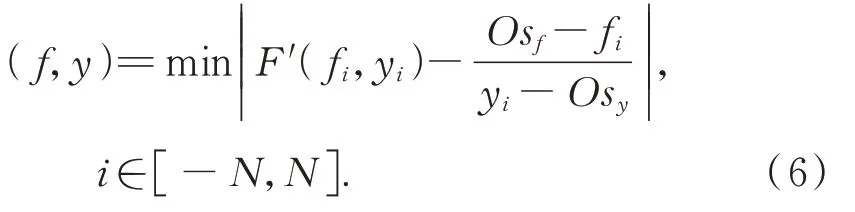
通过自适应调速飞刀切削模型可知，计算出的刀具回转中心轨迹可转换为进给速度。进给速度是通过两个相邻的刀具回转中心之间的距离除以固定的时间间隔来计算的。加工时沿进给方向的刀具轨迹点如图5所示。由于相同切削深度和斜率处下坡段的最大切屑厚度大于上坡段，所以下坡段的刀具轨迹点相比上坡段更加密集。瞬时进给速度会在X轴不同位置周期性波动，假设主轴转速为1 000 r/min，计算得到自适应调速飞刀切削的平均进给速度为4.36 mm/min，最小进给速度为1.67 mm/min，如图6所示。在相同的切削条件下，传统飞刀切削允许的最大进给速度要小于1.67 mm/min，才可以避免在最大切屑厚度处出现脆性断裂。因此，自适应调速的加工效率几乎是传统飞刀切削的2.5倍。

图5 切削路径回转中心位置Fig.5 Cutting path center of rotation position

图6 切削速度对比示意图Fig.6 Schematic diagram of cutting speed comparison

3 实验与结果

3.1 实验与检测设备

本实验的主要加工设备为Moore Nanotech超精密自由曲面加工机床（Nanotech350FG），如图7（a）所示。五轴机床床身由花岗岩制成，热变形小；底部由气垫支撑，可隔绝振动。主轴为带有C轴模式的气浮主轴，最高转速可达3 000 r/min，反馈精度为0.07″，主轴及径向跳动不大于12.5 nm，在100PSI时可吸附大约70 kg的零件。X，Y，Z为液体静压导轨，采用直线电机驱动，重复定位精度达300 nm，X，Y，Z方向的导轨行程分别为

350，150，300 mm。

加工后采用NikonMM 400型光学显微镜检测工件，如图7（b）所示。MM 400载物台型号6X4，行程为150 mm（X）×100（Y）mm，最大承载能力为10 kg。采用先进的LED光源，发光均匀且减小了光照热胀造成的测量误差，解决了拐边死角无法测量的问题。最后，工件采用Bruker GT-X型白光干涉仪进行测量，仪器外形图如图7（c）所示，放大倍数为0.5～200倍，数据可输出到MATLAB等其他分析软件中进行分析。

3.2 实验设计与结果仿真

实验材料为厚度为1 mm，晶向＜110＞的单晶硅片，其脆塑转变临界切深大约在110 nm，因此仿真设置临界切深为100 nm，以保证材料以塑性方式去除。同时采用刀尖圆弧半径为1.56 mm，前角为-25°的圆弧金刚石刀具。根据单晶硅塑性加工数学模型的仿真结果设计实验参数，如表1所示。

表1 自适应调速飞刀切削与传统飞刀切削的加工参数Tab.1 Parameters of self-tuned flying cutting and conventional flying cutting

图8是单晶硅飞刀切削塑性加工的数学模型。从图8可以看出，在微沟槽的不同位置，最大切屑厚度会发生改变。传统飞刀加工方法的最大切屑厚度会随着切屑深度与不同位置瞬时斜率的改变而改变，而自适应调速飞刀切削产生的最大切屑厚度始终保持恒定。

图8 塑性加工模型最大切屑厚度对比Fig.8 Comparison of maximum chip thickness of plastic working model

3.3 实验结果分析

为了验证所提出自适应调速飞刀切削方法在加工红外光学材料方面的优势，实验分别使用自适应调速飞刀切削方法和传统飞刀切削方法在单晶硅片上加工正弦曲线形微沟槽进行比较。自适应调速飞刀切削方法加工的微沟槽形貌如图9所示。在光学显微镜下观察到微沟槽下坡段、底部以及上坡段均无脆性断裂或裂纹的沟槽表面，可以验证自适应调速飞刀切削方法可在切削深度和微沟槽瞬时斜率变化的情况下以塑性方式加工微沟槽。

图9 自适应调速飞刀切削微沟槽的分段光学显微图像Fig.9 Segmented optical microscopic images for selftuned flying cutting micro-groove

从图10可以发现，通过白光干涉仪检测分析可得微沟槽沿着进给方向从开始加工的下坡段到结束的上坡段表面质量均匀且无微裂纹。微沟槽内表面粗糙度非常小，仅为18 nm左右。这表明自适应调速飞刀切削方法可制备表面质量均匀且光滑的表面。图9中带状条纹是由于飞刀切削加工间歇性切割过程产生的，超精密飞刀切削技术很好地保证了具有复杂结构的微沟槽表面的形状精度和表面均匀性。

图10 自适应调速飞刀切削微沟槽的分段白光干涉仪下粗糙度Fig.10 Surface roughness of micro-groove prepared by self-tuned flying cutting under white light interferometer

自适应调速超精密飞刀切削方法可以加工出光滑且均匀表面质量的微沟槽主要归功于其独特的切削机制，即在进给方向将最大切屑厚度与瞬时切削深度、斜率相匹配以自适应计算出每个刀具回转周期的位置。因此，尽管自适应调速飞刀切削方法中理论设置的进给速度为8 mm/min，相当于主轴沿X轴的移动速度，但由于额外的自适应调速运动，其瞬时进给速度不断变化，从而满足其加工特性。因此，尽管微沟槽局部的瞬时切削深度和斜率是不断变化的，但最大切屑厚度严格等于单晶硅的脆塑转变临界切深，从而保证了整个切削区域工艺的一致性并以塑性方式去除材料。

为了进一步的验证所提出的自适应调速飞刀切削方法在提高表面均匀性和加工效率方面的优势，实验还设置了不同进给速度下传统飞刀切削微沟槽的对比实验，实验结果如图11所示。在光学显微镜下可以明显地观察到，传统飞刀切削制备出的微沟槽沿进给方向下坡段出现了黑色斑点状的脆性断裂和微裂纹。在白光干涉仪下观察到了不均匀的表面质量和更大的表面粗糙度，为25 nm左右，如图12所示。这是由于在传统飞刀切削加工中，无法调节进给速度所形成的。在传统飞刀切削加工微沟槽时，每个刀具回转周期产生的最大切屑厚度会随着位置的变化而变化，如图2所示。与上坡段相比，下坡可形成较大的切屑厚度，在飞刀切削中，切削深度逐渐 增大的位置更容易产生脆性断裂。与自适应调速飞刀切削相比，即使在塑性加工区域，传统飞刀切削会产生更粗糙的表面。相反，由于自适应调速飞刀切削在进给方向的独特运动规律，可保证每次切削生成的最大切屑厚度一致，下坡段区域的瞬时进给速度比上坡段区域的瞬时进给速度慢得多。进给量的自适应调整是产生更平滑、更均匀表面质量的主要原因。

图11 进给速度3 mm/min下传统飞刀切削微沟槽的分段光学显微图像Fig.11 Segmented optical microscopic image of microgroove prepared by conventional flying cutting at 3 mm/min feed rate

图12 进给速度3 mm/min下传统飞刀切削微沟槽的分段白光干涉仪下的粗糙度Fig.12 Surface roughness of micro-groove prepared by conventional flying cutting at 3 mm/min feed rate under white light interferometer

当采用较大进给速度进行传统飞刀切削时，在沟槽的下坡段会产生程度更大的脆性断裂，并向沟槽底部扩展，其表面粗糙度在60 nm左右，如图13和图14所示。同时，从底部向上坡段的沟槽表面出现了黑色斑点状的脆性断裂和微裂纹，以及不均匀的表面质量。因此，为了加工出表面无裂纹的微沟槽，传统飞刀切削在主轴转速为1 000 r/min时的进给速度应小于8 mm/min。相比之下，自适应调速飞刀切削即使采用8 mm/min的进给速度，也能获得高质量的表面，不会产生脆性断裂，如图8所示。因此，自适应调速飞刀切削的加工效率是传统飞刀切削加工方法的近2.5倍。

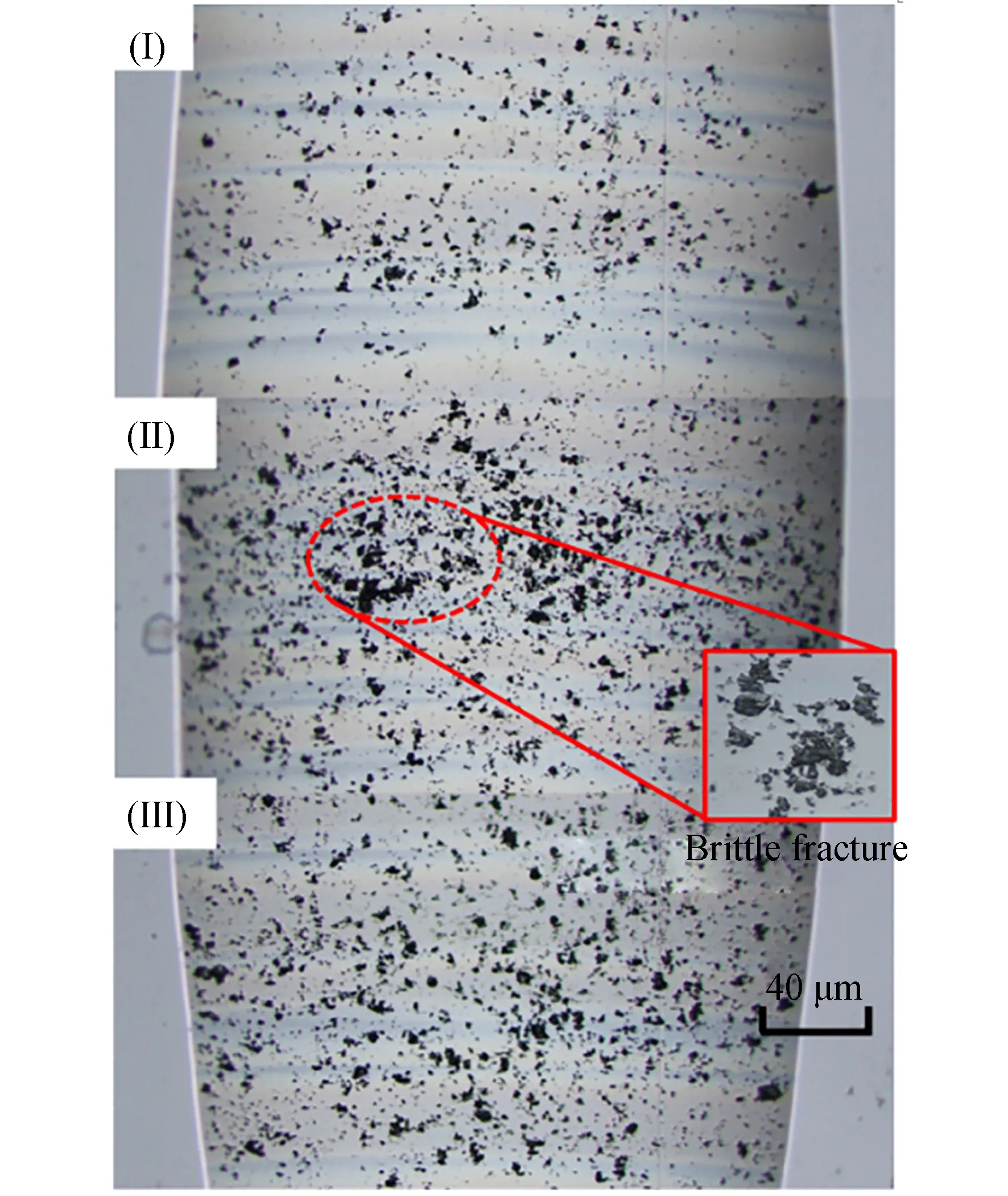
图13 进给速度8 mm/min下传统飞刀切削微沟槽的分段光学显微图像Fig.13 Segmented optical microscopic image for conventional flying cutting micro-groove at 8 mm/min feed rate

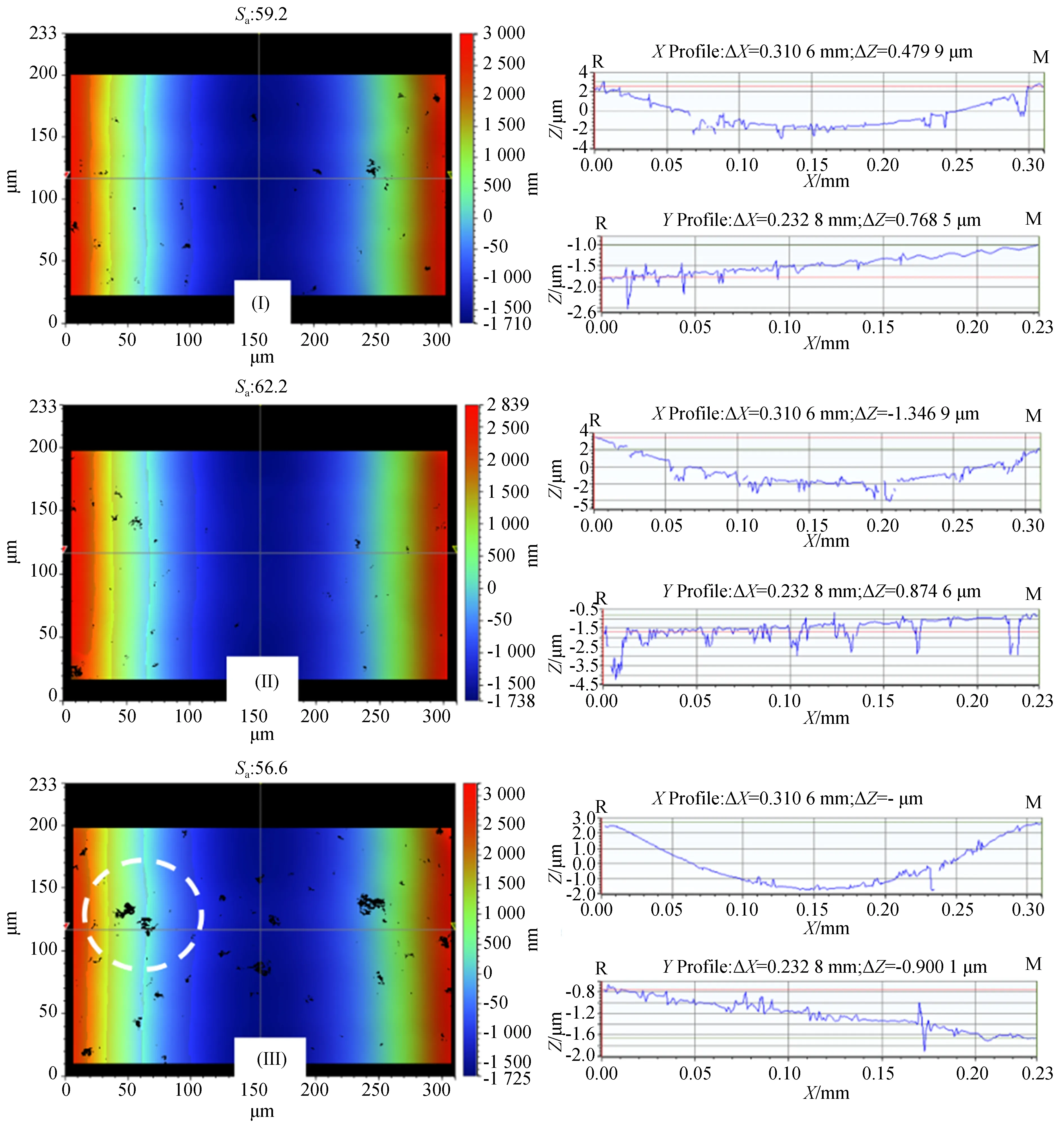
图14 进给速度8 mm/min下传统飞刀切削微沟槽的分段白光干涉仪下的粗糙度Fig.14 Surface roughness of micro-groove prepared by conventional flying cutting at 8 mm/min feed rate under white light interferometer

从本质上讲，任何微结构表面都具有表面高度和斜率多变的几何特征，其典型代表有凹凸微透镜、金字塔阵列等。自适应调速飞刀切削方法可以根据每个刀具回转周期产生切屑的最大切屑厚度匹配相应红外光学材料的脆塑转变临界切深，计算出加工表面所对应的回转中心位置，从而适配进给速度进行加工，因此适用于具有复杂几何特征的微结构表面。

4 结 论

为了实现微沟槽的塑性加工，同时提高加工表面质量和加工效率，本文提出了一种自适应调速超精密飞刀切削方法。该方法通过每个刀具回转周期产生切屑的最大厚度与材料脆塑转变临界切深相匹配，计算出每个刀具的回转中心，进而调整加工时的进给速度，保证整个微沟槽的表面质量，提高了加工效率。考虑飞刀切削塑性加工模型和切削生成理论数学模型，提出了相应的刀具轨迹算法。为了验证该方法的有效性，分别使用该方法和传统飞切切削在单晶硅上用不同参数加工微沟槽。与传统飞刀切削方法相比，自适应调速飞刀切削方法加工出的微沟槽表面均匀性更高，粗糙度为18 nm。为避免在下坡段和切削深度大的位置产生脆性断裂，传统飞刀切削需要非常小的进给速度加工。相比之下，自适应调速飞刀切削方法在满足表面质量的同时，可以极大地提高平均进给速度，加工效率为传统飞刀切削的2.5倍。该方法有效克服了现有超精密飞刀切削技术在加工红外光学材料微结构表面时因提高进给速度而产生脆性断裂的局限性。