交直流配电网系统中准Z源网络的小信号模型分析与验证*

张金鹏,张仁和,何玉鹏,朱 林,冯晓群

(国网宁夏电力有限公司，宁夏 银川 750001)

0 引 言

近些年，以国家电网为代表的能源电力企业正不断研发满足配电网中电动汽车应用需求的DC-AC变换器[1-2]。因此，电压源型逆变器(VSI)得到了广泛的应用，通过适当调节VSI的直流链电压即可提高电动汽车牵引驱动系统的整体效率。众所周知，VSI属于降压型逆变器[3-4]，其输出电压总是小于直流链电压，即电压增益较低。然而，根据交流负载的要求，VSI需要输出较高的电压以满足负载需求。因此，部分学者引入DC-DC变换器[5]来解决这一问题。然而，这种解决方案增加了系统的投资成本，降低了系统运行效率。

Z源逆变器(ZSI)是一种新型的具有降压和升压功能的单级式电力电子功率变换器，已被用于含有燃料电池的能量转换系统和带有整流器的电机驱动系统。与传统的电压源和电流源逆变器相比，ZSI的唯一区别在于其含有电感和电容构成的Z型阻抗网络，连接着输入电源和逆变器回路。这种独特的阻抗网络允许同一相支路内的两个开关管同时导通，以引入直通状态，进而提高逆变器输出电压[6-7]。

然而，传统的Z源逆变器存在升压能力有限、电感电流较大、电容应力高等缺点。基于这些不足，研究者提出了各种准Z源拓扑[8-9]。文献[10]在传统Z源拓扑的基础上提出了一种新的Z源拓扑，它可以降低Z源网络电感的耦合度，抑制电感电流冲击。文献[11]提出了一种电感升压型准Z源拓扑，其升压系数较大，可以显著提高逆变器输出电压水平，满足现代工业的需求。文献[12-14]提出的几种准Z源拓扑可以在升压比恒定的情况下显著降低Z源网络的电容电压和电感启动电流，提高系统经济性。鉴于上述文献中准Z源拓扑的特性，本文以文献[12]中的准Z源网络为研究对象，研究其模型特征，可为该种类型的准Z源逆变器的控制策略提供理论参考，以提高其性能。

目前，较多文献中已经研究了变换器的建模方法。其中，最常用的方法是小信号模型分析[15-16]。小信号模型分析是研究系统受小扰动时动态响应的一种数学方法，利用该方法可以清晰地呈现部分参数变化对系统动态性能的影响。另外，状态空间法[17-18]也为模型建立提供了较大的方便，该方法根据系统拓扑建立相应的状态空间方程，清晰地明确了各种变量之间的数学关系。基于此，本文首先利用状态空间法建立了含有电感电流和电容电压变量的状态方程；其次，利用小信号模型方法推导出这两种变量的传递函数，并分析相应的Bode图和零极点分布以获得电感参数和电容参数影响系统动态性能的变化特征。最后，利用MATLAB/Simulink软件仿真的结果和物理样机试验验证了本文小信号模型分析的正确性。

1 系统拓扑和工作原理

图1即为文献[12]所提出的准Z源逆变器拓扑结构。其中，直流电源Udc通过上下串联电容器Cs1、Cs2连接到准Z源网络，然后再连接到传统的二极管箝位三电平逆变器电路。VD1和VD2是准Z源网络的导通二极管，L1～L4是准Z源网络电感，C1～C4是准Z源网络电容。VTA1～VTA4、VTB1～VTB4和VTC1～VTC4分别是A相、B相和C相桥臂上的IGBT开关。VDA1、VDA2、VDB1、VDB2和VDC1、VDC2分别是三电平逆变器的6个箝位二极管。

图1 准Z源三电平逆变器拓扑

当直通时间等于0时，图1所示拓扑中开关管的导通状态与传统三电平逆变器相同，此时工作原理如图2(a)所示，这种状态也被称为准Z源网络的非直通状态。除了非直通状态外，准Z源三电平逆变器还存在上直通状态和下直通状态，如图2(b)和图2(c)所示。以图2(b)为例，此时开关管VTX1、VTX2和VTX3(X=A, B, C)同时导通，二极管VD1和VDX1导通，VD2和VDX2断开。同样地，图2(c)为下直通状态，其工作原理是VTX2、VTX3和VTX4同时导通，VD2和VDX2导通，VD1和VDX1断开。

图2 准Z源网络的工作原理图

根据文献[12]可知，此种拓扑网络中电容电压为

(1)

式中：UC为准Z源网络的电容电压；D0为直通占空比。

另外，准Z源网络输出直流电压为：

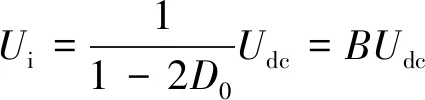
(2)

式中：Ui为准Z源网络升压侧电压；B为升压比。

2 状态空间法

令通过电感L1和L2的电流为IL1和IL2，通过电感L3和L4的电流为IL3和IL4，UC1、UC2、UC3和UC4分别是电容C1、C2、C3和C4的电压。中性线上方的负载电流为Iin1，下方的负载电流为Iin2。同时，假设逆变器桥臂和负载可由两个等效电流源代替。根据网络的对称性，准Z源拓扑中存在以下数学关系假设：

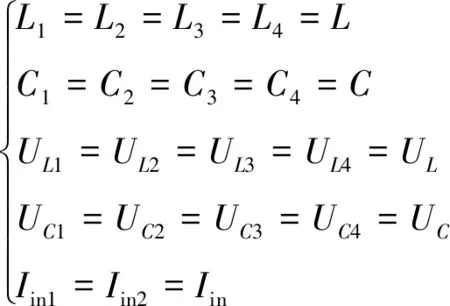
(3)

根据电路理论，图2(a)中非直通状态时有以下状态方程：

(4)

同理，图2(b)和图2(c)中的上直通状态和下直通状态有以下状态方程：

(5)

(6)

式(4)～式(6)所示状态方程是时变的。为了得到新拓扑在一个开关周期内的状态方程，需要对上述方程进行分段平均化处理。处理后可到新拓扑在一个周期内的状态平均方程：

(7)

此时，令状态变量x=[ILUC]T，输入变量u=[UdcIin]T，式(7)可化简为

(8)

另外，假设存在以下状态空间关系：

(9)

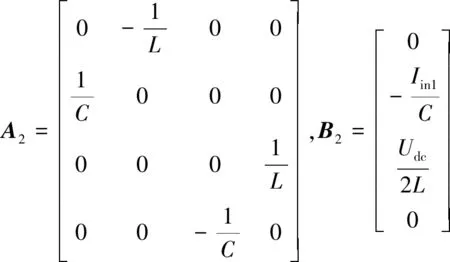
(10)

(11)

结合式(8)～式(11)可得：

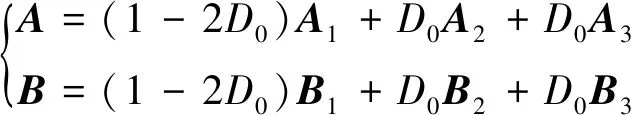
(12)

3 小信号模型分析方法

迄今已经提出了多种功率转换器的建模方法，其中以小信号模型方法最为普遍。因此，本节将利用小信号模型方法研究参数阶跃变化的开环系统的暂态特性，并通过加入扰动变量，建立状态扰动方程来研究目标对象。

依据以上的分析，可得含有实际变量的状态方程为

(13)

式中：

(14)

将式(14)代入式(8)可得：

(15)

对式(15)两边同做拉式变换，可得：

x*(s)=(sI-A)-1{Bu*(s)+[(A2+

(16)

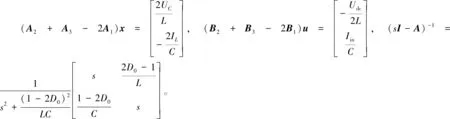
进而展开式(16)，可得如下关于实际变量电感电流IL和电容电压UC的状态方程：

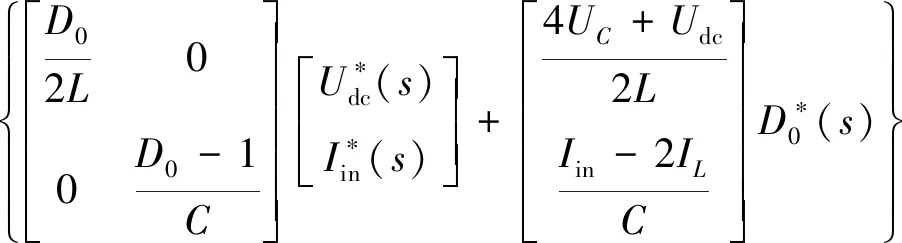
(17)

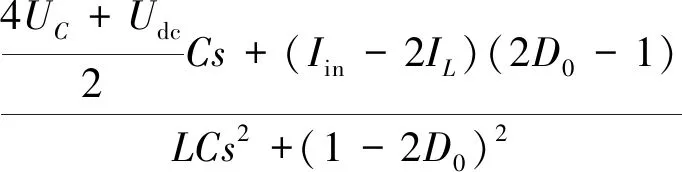
(18)

(19)

由式(18)和式(19)可知，两种传递函数的方程中存在UC、Udc、D0、Iin以及IL5种变量。其中，UC、Udc以及D0满足式(1)所示的关系，且通常情况下Udc和D0是提前设定的。因此，研究式(18)和式(19)所示的传递函数需要探究Iin和IL两个变量之间的关系。

稳态工作点处存在A*x+B*u=0，进而可到以下电感电流的方程：

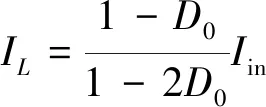
(20)

为了详细探究上述两种传递函数零极点的变化情况，以下将通过改变L、C以及D0等参数的大小探究不同参数设定下两种传递函数的动态特性。部分参数设置如表1所示。

表1 参数设定

图3为准Z源网络参数变化时式(18)所示的电感电流传递函数零极点变化情况。其中，图3(a)为电容参数由1 000 μF增加至4 000 μF的零极点变化。由图3(a)可知，随着电容参数的增加，传递函数的极点逐渐向实轴移动，表明大的电容参数将会使得电感电流的稳定性减弱；同理，电容参数增加时，传递函数的零点逐渐向虚轴移动，这一现象进一步验证了上述分析的正确性。然而，尽管电容参数变化带来了这种稳定性减弱的情况，但所有的零极点都位于左半平面内，系统总体来说处于稳定的状态。图3(b)是电感参数变化时零极点的分布情况。由图3(b)可知，随着电感参数的增加，传递函数的极点逐渐向实轴移动，表明大的电感参数将使得电感电流的稳定性减弱。此时，传递函数的极点位置保持不变，始终位于左半平面内，表明系统总体来说是保持稳定的。图3(c)展现了直通占空比发生变化时传递函数的零极点分布情况。由图3(c)可知，随着占空比的增加，传递函数的极点逐渐向实轴移动，表明大的占空比将同样使得电感电流的稳定性减弱。此时，传递函数的零点逐渐向虚轴移动，这验证了上述分析的系统稳定减弱这一结论。

图3 准Z源网络参数变化时式(18)传递函数零极点变化情况

图4是准Z源网络参数变化时式(19)所示传递函数的零极点分布情况。其中，图4(a)是电容参数由1 000 μF增加至4 000 μF时，传递函数的零极点的动态变化情况。由图4(a)可知，随着电容参数的增加，传递函数的极点逐渐向实轴移动，表明较大的电容参数将使得电容电压的稳定性减弱。此时，传递函数的零点始终保持在右半平面。图4(b)是电感参数变化时，传递函数的零极点分布情况。由图4(b)可知，随着电感参数的增加，传递函数的极点逐渐向实轴移动，表明大的电感参数将减弱电容电压的稳定性。此时，传递函数的零点逐渐向虚轴移动，这也充分证明了上述分析的正确性。图4(c)展现了直通占空比由0.1增加至0.5时，传递函数零极点的分布情况。由图4(c)可知，随着占空比的增加，传递函数的变化情况与图4(b)相同，表明较大的占空比也会使得电容电压不稳定。

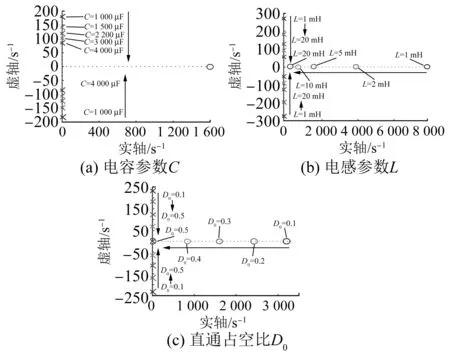
图4 准Z源网络参数变化时式(19)传递函数零极点变化情况

上述分析讨论了准Z源网络参数对电感电流和电容电压稳定性的影响，下面将重点分析准Z源网络参数对电感电流和电容电压响应速度的影响。

图5给出了电容参数、电感参数以及直通占空比变化时电感电流传递函数的Bode图分布情况。由图5可知，随着电容、电感以及占空比的增加，电感电流传递函数的幅值逐渐增加，且参数值越大，其幅值尖峰增益越大，表明较大的电容、电感和占空比将使得电感电流的稳定性减弱，这与前述分析基本一致。同时，随着参数的增加，传递函数Bode图在高频处的变化趋势逐渐平缓，表明系统的响应速度降低。

图5 准Z源网络参数变化时式(18)传递函数的Bode图

同理，图6给出了电容、电感以及占空比变化时电容电压传递函数的Bode图分布情况。由图6可知，电容参数、电感参数以及占空比增大时，传递函数的幅值增益曲线逐渐向左移动，表明系统的响应速度降低，即较大的电容参数、电感参数以及占空比会降低电容电压的响应速度。

图6 准Z源网络参数变化时式(19)传递函数的Bode图

4 仿真和实验

4.1 仿真验证

为了验证上述理论分析的正确性，在MATLAB/Simulink软件中搭建了图1所示的准Z源拓扑，部分仿真参数如表1所示。另外，开关频率fs设定为2.5 kHz；直通占空比D0设定为0.3，则由式(2)可得出升压因子B=2.5；调制比M=0.8，三相负载电阻为50 Ω。以下将从电容参数、电感参数以及直通占空比发生变化时电感电流波形和电容电压波形两方面重点分析验证。

图7是电容、电感参数以及占空比变化时的电感电流波形。其中，图7(a)是电容参数由1 000 μF增加至4 000 μF时的电感电流波形。由图7(a)可知，随着电容参数的增加，电感电流趋于稳定的时间延长，这也验证了上述理论分析得出的较大的电感参数会降低系统响应速度的结论。图7(b)是电感参数由1 mH增加至20 mH时的电感电流波形。由图7(b)可知，随着电感参数的增加，电感电流趋于稳定的时间延长，这同样验证了上述结论，并与理论分析基本一致。图7(c)是占空比D0由0.1增加至0.4时的电感电流波形。由图7(c)可知，较大的占空比同样使得电感电流趋于稳定的时间延长，这与图3(c)和图5(c)的分析基本一致。

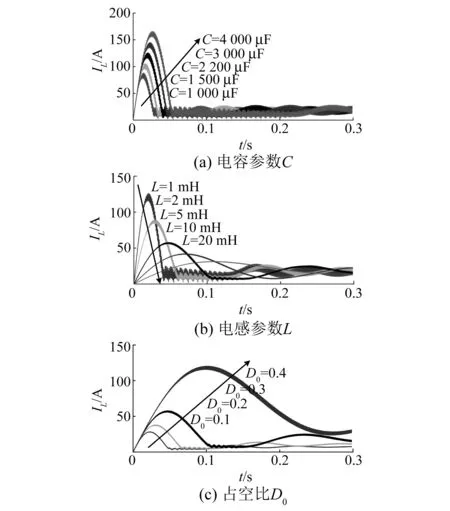
图7 电容、电感参数以及占空比变化时准Z源网络的电感电流波形

图8是电容、电感参数以及占空比发生变化时电容电压波形。其中，图8(a)是电容参数发生变化时的电容电压波形。仿真中设定D0为0.3，则由式(2)可以推出电容电压为150 V。由图8(a)可知，随着电容参数的增加，其稳定时电容电压的数值都接近150 V，但是较大的电容参数使得系统稳定的时间延长。例如，电容参数为1 000 μF时，电容电压约在0.1 s趋于稳定；但是，电容参数为4 000 μF时，电容电压约在0.22 s趋于稳定。图8(b)为电感参数发生变化时的电容电压波形。由图8(b)可知，较大的电感参数也会使得电容电压趋于稳定的时间延长，这与上述理论分析基本一致。图8(c)是占空比D0由0.1增加至0.4时的电容电压波形。由式(2)可知，D0由0.1增加至0.4时，电容电压依次为25 V、66.67 V、150 V和400 V。由图8(c)可知，电容电压稳态时的数值基本与上述理论值一致。但是，较大的占空比延长了电容电压趋于稳定的时间，即响应速度较低，这与图4(c)和图6(c)的分析也基本一致。

图8 电容、电感参数以及占空比变化时准Z源网络的电容电压波形

4.2 物理样机试验

为了验证上述理论和仿真分析的正确性，本文与相关逆变器公司合作搭建了准Z源逆变器硬件试验平台。试验中，微电源用直流稳压电源代替，设定直流电压Udc=400 V。实际中无法较好地修改电容参数和电感参数，因此本文仅通过改变直通占空比D0的数值来研究准Z源网络的动态特性。另外，该实验平台的控制信号由 TMS320F28335 型的DSP控制器产生，三相逆变器的开关器件选用英飞凌IKW40N120H3，开关频率为2.5 kHz。

图9为试验中将直通占空比D0由0.3降低至0.1时的电感电流和电容电压波形。其中，图9(a)为电感电流波形，图9(b)为电容电压波形。由式(2)可知，占空比为0.3和0.1时，所对应的电容电压分别为150 V和25 V。由图9(b)可知，电容电压数值基本与上述理论值一致。同时，无论是电感电流还是电容电压，占空比D0由0.3降低至0.1时，其动态变化过程较快，即验证了上述仿真和理论分析的结论：较低的占空比可以提高系统响应速度。

图9 占空比D0由0.3降低至0.1时的电感电流和电容电压

图10是试验中将直通占空比D0由0.1增加至0.3时的电感电流和电容电压波形。其中，图10(a)为电感电流波形，图10(b)为电容电压波形。由图10(b)中的电容电压波形可知，其试验值与理论值基本一致。但是比较图9和图10可知，直通占空比D0由0.1增加至0.3时，电感电流和电容电压的动态变化过程的时间明显比D0由0.3降低至0.1对应的过程长，即响应速度较慢。这一现象同样证明了上述仿真和理论分析的结论：较大的占空比会延长电感电流和电容电压动态变化的时间。

图10 占空比D0由0.1增加至0.3时的电感电流和电容电压

5 结 语

本文着重分析了一种应用于配电网中准Z源三电平逆变器的暂态特性。利用状态空间法和小信号模型方法推导出准Z源网络的电感电流传递函数和电容电压传递函数。通过理论分析和相关仿真、试验，得出以下结论：(1)配电网中准Z源网络采用较大的电感参数和电容参数会降低系统的稳定性和动态响应速度。(2)配电网中准Z源网络采用较大的占空比会降低系统的稳定性，延缓系统的动态变化过程。

本文得出的结论可为应用于配电网中该种类型的准Z源逆变器的参数设计提供一定的思考。