基于Weil和的一类线性码的研究

卢虹杨淑娣张同慧

(曲阜师范大学 数学科学学院,山东 济宁 273165)

线性码是一类重要的纠错码,在密码学上有广泛的应用,尤其是较小重量的线性码.由于线性码的重量分布不仅可以确定其最小距离,反映其检错和纠错能力,而且包含了码的检错和纠错失误率的重要信息,因此研究较少重量线性码的重量分布具有重要的意义.

丁存生等[1]提出了线性码的一般构造方法,其表示如下:定义Fq是具有q个元素的有限域,其中q=pm,p是一个奇素数,m为正整数,Tr为Fq到Fp的迹函数.设集合D={d1,d2,…,dn}⊆Fq,构造线性码CD={c(a)=(Tr(ad1),Tr(ad2),…,Tr(ad1)):a∈Fq},集合D称为码CD的定义集.此后,国内外学者利用此方法构造了许多类较少重量的线性码[2-5].

简高鹏等[2]选择定义集D={(x,y)∈Fq2{(0,0)}:Tr(x+ypu+1)=0},其中u为正整数,定义了p元线性码

对于α,β∈Fq,扩展定义集

1 预备知识

1.1 Gauss和

1.2 Weil和

1.3 Pless 幂恒等式

2 主要结果

主要给出线性码的参数和重量分布,其证明将在第3部分给出.

定理1 若α≠0,β=0,由式(1)和式(2)定义的码CD是参数为[p2m-1,2m,(p-1)p2m-2]的二重线性码,其重量分布如表1所示.

表1 定理1中码C D 的重量分布Tab.1 Weight distribution of the linear code in theorem 1

定理2 若α≠0,β≠0,当m/d为奇数且d为奇数时,码CD是参数为[p2m-1,2m,(p-1)p2m-2-p(3m-3)/2]的三重线性码,其重量分布如表2所示.

表2 定理2中码C D 的重量分布Tab.2 Weight distribution of the linear code in theorem 2

表3 定理3中码C D 的重量分布Tab.3 Weight distribution of the linear code defined in theorem 3

表4 定理4中码C D 的重量分布Tab.4 Weight distribution of the linear code in theorem 4

表5 定理5中码C D 的重量分布Tab.5 Weight distribution of the linear code in theorem 5

定理6 若α=0,β≠0,当m/d为奇数且d为奇数时,码CD是参数为[p2m-1+pm-1G(η)G(ηp)η(-β),2m]的三重线性码,其重量分布如表6所示.

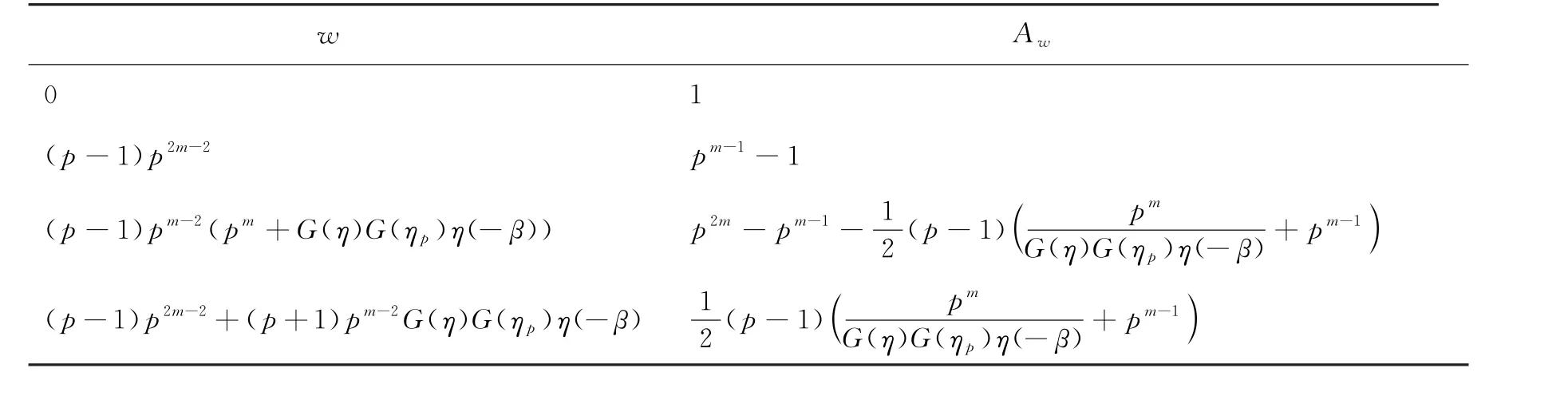
表6 定理6中码CD 的重量分布Tab.6 Weight distribution of the linear code in theorem 6

定理7 若α=0,β≠0,当m/d为奇数且d为偶数时,码CD是参数为[p2m-1-pm-1G(η)η(β),2m]的三重线性码,其重量分布如表7所示.

表7 定理7中码C D 的重量分布Tab.7 Weight distribution of the linear code in theorem 7

表8 定理8中码C D 的重量分布Tab.8 Weight distribution of the linear code in theorem 8

定理9 若α=0,β≠0,当m/d为偶数且β(q-1)/(pd+1)=(-1)s/d时,码CD是参数为[p2m-1+(-1)s/dpm+s+d-1,2m]的三重线性码,其重量分布如表9所示.

表9 定理9中码C D 的重量分布Tab.9 Weight distribution of the linear code in theorem 9

通过一些实例验证了结果的正确性,根据Griesmer界知,定理1中存在最优码,参数见表10.

表10 定理1中的最优码Tab.10 Optimal codes in theorem 1

3 主要结果的证明

4 结论

本文通过选取适当的定义集,构造了一类新的二重或三重线性码,是对文献[2]结果的进一步扩展,根据Griesmer界验证了其中一些码是最优码.