神经网络超参数优化的删除垃圾神经元策略*

黄颖 顾长贵 杨会杰

(上海理工大学管理学院,上海 200093)

随着深度学习处理问题的日益复杂,神经网络的层数、神经元个数、和神经元之间的连接逐渐增加,参数规模急剧膨胀,优化超参数来提高神经网络的预测性能成为一个重要的任务.文献中寻找最优参数的方法如灵敏度剪枝、网格搜索等,算法复杂而且计算量庞大.本文提出一种超参数优化的“删除垃圾神经元策略”.权重矩阵中权重均值小的神经元,在预测中的贡献可以忽略,称为垃圾神经元.该策略就是通过删除这些垃圾神经元得到精简的网络结构,来有效缩短计算时间,同时提高预测准确率和模型泛化能力.采用这一策略,长短期记忆网络模型对几种典型混沌动力系统的预测性能得到显著改善.

1 引言

深度学习被广泛应用于多学科领域,极大地提高了人们对复杂系统的认识.随着应用场景日益复杂,数据量和系统特征量增多,网络规模(层数、神经元个数和神经元之间的连接)日益膨胀,算法复杂度和计算量也因此在指数增长,通常用月或年来计算.而大规模的参数,也意味着过拟合问题,从而降低习得的模型的泛化能力.超参数优化,也就是通过优化网络结构,得到一个精简的网络结构,在计算时间可接受的条件下,显著提高预测水平,达到性能最优,成为当前人工智能领域一个基本而迫切需要解决的任务.

目前网络结构优化大致分为两种类型.一是基于相关参数和评价指标的变化情况直观调整网络结构,如拟合精度等指标的网格搜索法.这类方法理论上要遍历所有参数,耗时巨多,远超当前计算能力.实际中往往按照一定比例枚举参数取值,这又极易跳过最佳参数.二是基于一些高效的优化算法,如贝叶斯优化[1]、灵敏度和相关性剪枝相结[2,3]、学习率优化[4]、径向基函数优化[5]、多核极端学习机[6]、注意力机制引进[7]、扩展储量计算分化神经元[8]以及一些自适应算法[9]等,来提升训练效率.在广泛采用的灵敏度剪枝中,轮流删除节点操作意味着庞大的计算量.为避免大计算量而采用的工程近似方法,易导致节点误删除[10].

本文提出神经网络超参数优化的“删除垃圾神经元策略”.这一策略依据的一个简单事实是,神经元在时间序列预测中贡献是不一样的.给定一个初始的网络结构,并对它进行训练,在权重矩阵中权重平均值小的神经元,在预测中的贡献可忽略不计,称为垃圾神经元.从这一原始的神经网络中删除这些垃圾神经元,简化网络结构,来达到减小计算量、提高预测能力、增强泛化的目的.采用这一策略对长短期记忆网络(LSTM)模型的网络结构进行了优化.LSTM 模型[11]作为循环神经网络(RNN)的改进,既能记住短期信息,又能记住长期信息,克服了RNN 模型在时间跨度过长时容易存在梯度爆炸或梯度消失的问题,被广泛应用于时间序列分析,如自然语言处理(NLP)、语音识别、金融数据预测等.对Logistic,Henon,Rossler 三种典型混沌系统的预测表明,这一策略可以有效改善LSTM的预测性能.

2 长短期记忆模型

如图1(a)所示[12],LSTM 网络包含输入层、隐藏层和输出层,每一层由多个单元组成.在隐藏层的每个单元加入记忆细胞,并通过输入门、遗忘门和输出门来控制状态.

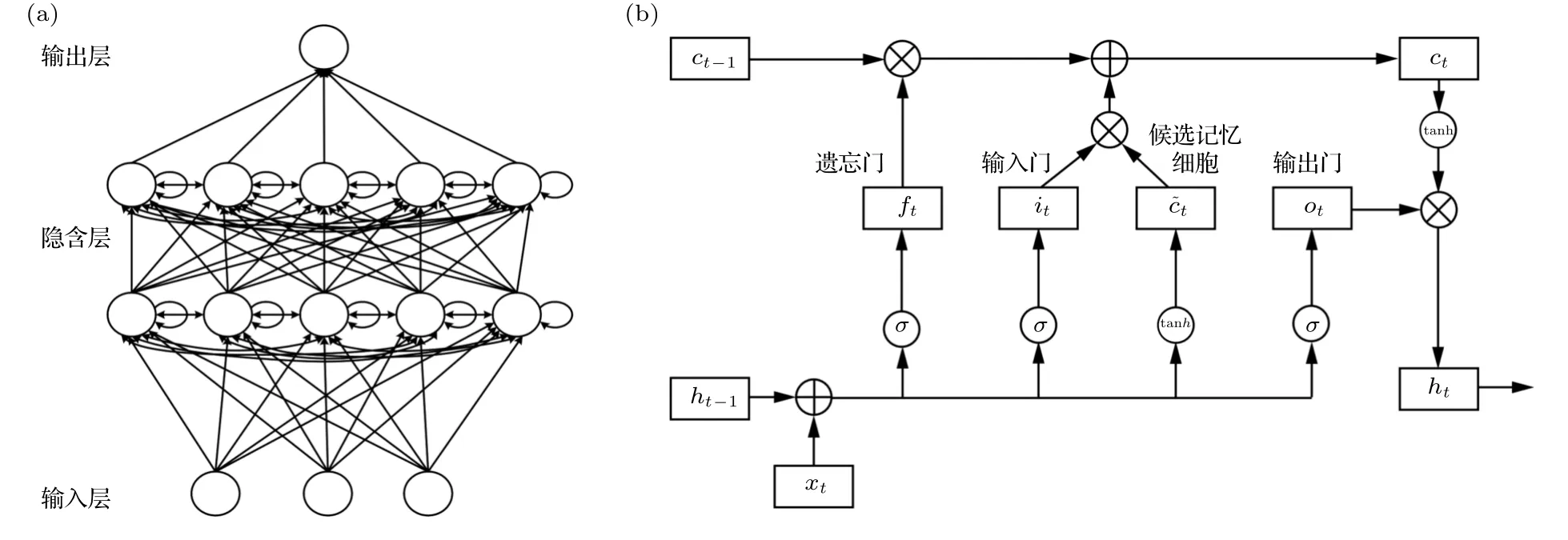
图1 LSTM 神经网络 (a)LSTM 模型网络结构;(b)单元内部运行逻辑Fig.1.LSTM neural network: (a)network structure of LSTM;(b)run logic inside the cell.

其中,⊙为向量元素相乘.

ft控制ct-1到当前时间步的信息流动,it控制到当前时间步的信息流动,ot控制当前时间步的ct到ht的信息流动.如当ft接近1 且it接近0 时,过去的记忆细胞信息将会一直保留,可更好地捕捉时间序列中时间步较大的样本间的依赖关系.当ot接近1 时,ct的信息将传递至ht供输出层使用;当ot接近0 时,ct的信息将自己保留.

3 删除垃圾神经元策略

作为实例,我们考察了LSTM 对混沌系统预测的能力.采用删除垃圾神经元策略,简化了隐藏层结构,显著提高了预测能力.删除垃圾神经元策略的具体操作步骤如下.

1)搭建含有两层LSTM和两层全连接层的模型,用网格搜索法寻找最佳参数的大致取值范围.由于模型中参数众多,若以等差为1 的序列遍历,模型训练耗时将长达数年,因此以等比序列 2n或其他步长遍历参数.

2)由于初始权重随机生成,单次训练结果没有统计意义,本文滑动读取样本分别进行多次训练,并计算各组参数的预测准确率(预测值的涨跌趋势和真实值涨跌趋势相同的样本量占总预测样本量的比值)、R方值、MSE 等评价指标的平均值并输出.根据准确率和R方值最高、MSE 最低、神经元数最少的原则,初步选取最佳参数组合,包括各层神经元数、迭代次数、batch、dropout 等.

3)用初步选取的最佳参数组合训练模型并输出网络权重,分析各组权重代表的意义,明确垃圾神经元.删除垃圾神经元得到简洁的网络结构,比较模型效果.

4)以不同的权重阈值为界,定义垃圾神经元,尽量使每组阈值删除的神经元数分布均匀;比较精简网络后的预测效果,找到能最大程度提升模型性能的阈值.

4 计算实验

具体考察Logistic[13],Henon[14]和Rossler[15]三个典型混沌系统的LSTM 预测.Takens 嵌入定理指出,混沌系统的每一维度变量都包含整个系统的长期演化信息[16].因此,我们从每个系统的动力学轨迹中,只抽取一维数据作为样本,以使得各系统实验结果之间具有可比性.

4.1 数据处理

Logistic 模型也称虫口模型,其差分方程表示为

随着参数µ的增加,系统发生倍周期分叉,当µ∈[3.569,4],系统出现混沌现象.由于Logistic 系统随着参数取值不同,混沌程度也不同,因此µ分别取3.6,3.7,3.8,3.9,3.99 生成样本量为50000 的一维时间序列数据.图2(a)给出的是µ取3.9 时的轨迹.

Henon 映射的迭代表达式为

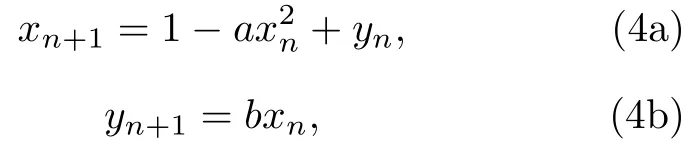
其 中a=1.4,b=0.3.x和y初始值取 为0.01 生成样本量为50000 的时间序列数据.图2(b)中横轴表示系统的迭代次数,图像给出迭代前100 次得到的x,y值构成的轨迹.

Rossler 系统是一连续混沌动力系统,其微分方程组为

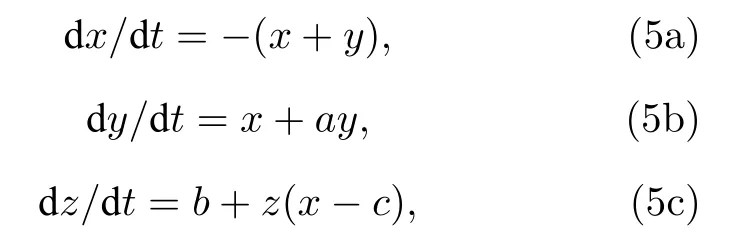
其中参数a取0.2,b取0.4,c取5.7.以xyz0为初始值,采用四阶Runge-Kutta 方法[17],以0.001为步长模拟出t∈[0,500] 的运动轨迹,图2(c)给出前10000 个时间点的轨迹.为使样本量同另外两个系统一致从而结果具有可比性,本文再以10 为抽样步长得到50000 条数据作为样本.

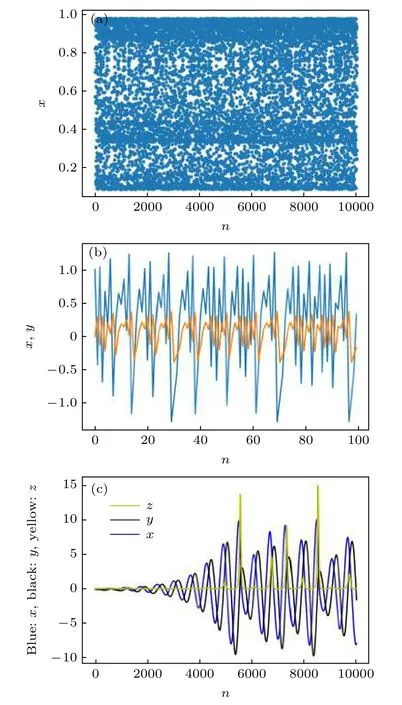
图2 混沌时间序列 (a)Logistic 系统,µ=3.9;(b)Henon系统;(c)Rossler 系统Fig.2.Chaotic time series: (a)Logistic system,µ=3.9;(b)Henon system;(c)Rossler system.

对数据进行归一化处理.三个系统的训练集样本量均取为5000.由于LSTM 模型预测较长时间后的数据意义不大,因此选取测试集样本量为15.为使实验结果具有统计意义,以一定步长滑动选取样本进行多次实验.本文分别以100,200,300,···,4000 作为滑动窗口训练10 次模型,取10 次预测准确率的均值为最终结果,发现不同滑动窗口对应的平均预测准确率在70%附近上下波动,可见滑动窗口大小对预测结果没有显著影响.为充分利用并均匀覆盖已有样本,选取4000 为滑动窗口进行预测,如第一批样本以1—5000 条数据作为训练集,5001—5015 条数据作为测试集;第二批样本以4000—9000 条数据作为训练集,9001—9015 条数据作为测试集;以此类推,共训练10 批样本(最后一批样本以40000—45000 条数据作为训练集,45001—45015 条数据作为测试集).最终以10 次预测评价指标的均值作为模型最终的评价指标.

4.2 LSTM 模型建立

三个系统初步选取的最佳参数组合如表1 所列.其中,train 为训练集样本量;test 为测试集样本量;win 为滑动窗口数,表示每次观测到的样本数,如win 为3 表示第一批输入模型的样本为x1,x2,x3,下一批为x2,x3,x4,以此类推;L1为第一层LSTM 输出神经元数;L2为第二层LSTM 输出神经元数;D1为第一层全连接层输出神经元数;D2为第二层全连接层输出神经元数,即最终输出.

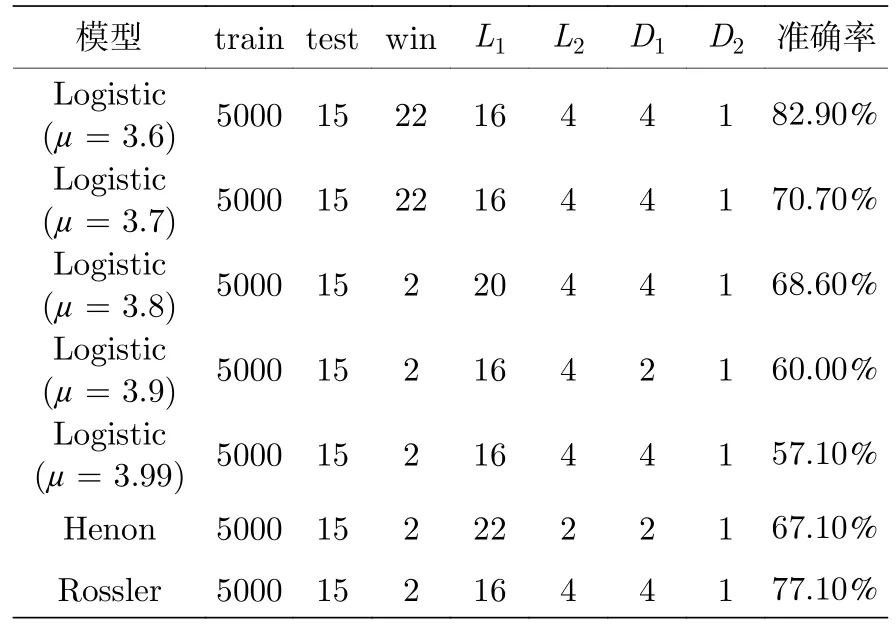
表1 模型参数及结果Table 1.Parameters and results of the models.

在多数模型中,以较为常见的步长2n进行网格搜索得到的预测准确率是相对较高的,第一层网络的最优参数基本稳定在16 个神经元,对于训练集样本数为5000 的数量级来说是足够的,更复杂的网络容易造成过拟合;当然也有部分模型以2n为步长网格搜索时未能得到不错的预测效果,文中也会视情况选择其他步长,如µ3.8 的Logistic 模型,以10 为步长进行网格搜索可得到更好的预测效果,此时便在网格搜索最优参数为20 的基础上进一步优化超参数.

4.3 权重分析

全连接层的权重较为简单,在此不做分析.LSTM 层的权重包含三个张量: kernel,recurrent_kernel和bias,每个张量的维数为4×神经元数,依次为input_gate,forget_gate,cell和output_gate,权重拆分如表2 所列.

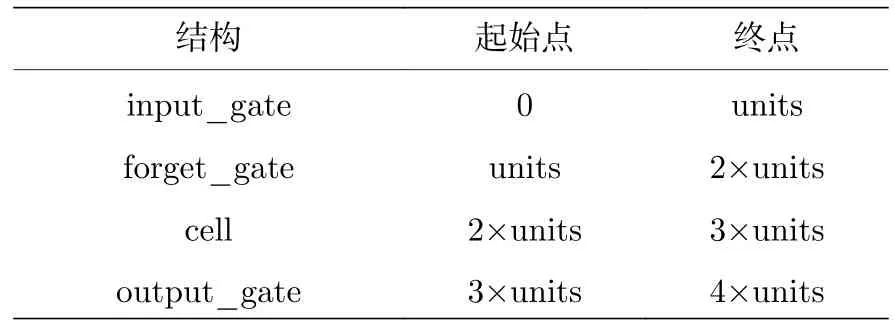
表2 权重结构拆分Table 2.Weight structure resolution.

根据(1a)式—(1d)式可知,output_gate 权重直接关系到神经元的最终输出结果,因此对该权重做热度图以便于分析.以Logistic 系统中µ3.99为例,LSTM 输出层神经元数为16,输出门对应的权重矩阵维数为16×16.如表3 所列,第一行权重表示隐藏层输入的16 个神经元对输出的第一个神经元影响大小,第一列则表示隐藏层输入的第一个神经元对输出的16 个神经元的影响大小,均值行为每个输入神经元对所有输出神经元的权重绝对值的平均值,均值越小的神经元可以理解为对整个输出层的影响越小.

在python 中用imshow 函数绘制出该权重矩阵对应的热图.首先对表3 中每一行的权重数据分别进行归一化,便于分析隐藏层输入神经元对各个输出神经元的影响大小;接着绘制热图,颜色越黄权重越高,颜色越蓝权重越低.为了更直观地体现各输入神经元的重要性,进一步绘制如图3和图4所示的热图.同样地,颜色越黄权重均值越高,表示该输入神经元给整个输出层提供的信息越多;颜色越蓝权重均值越低,表示该输入神经元给整个输出层提供的信息越少,均值足够低的输入神经元即可作为垃圾神经元删除.

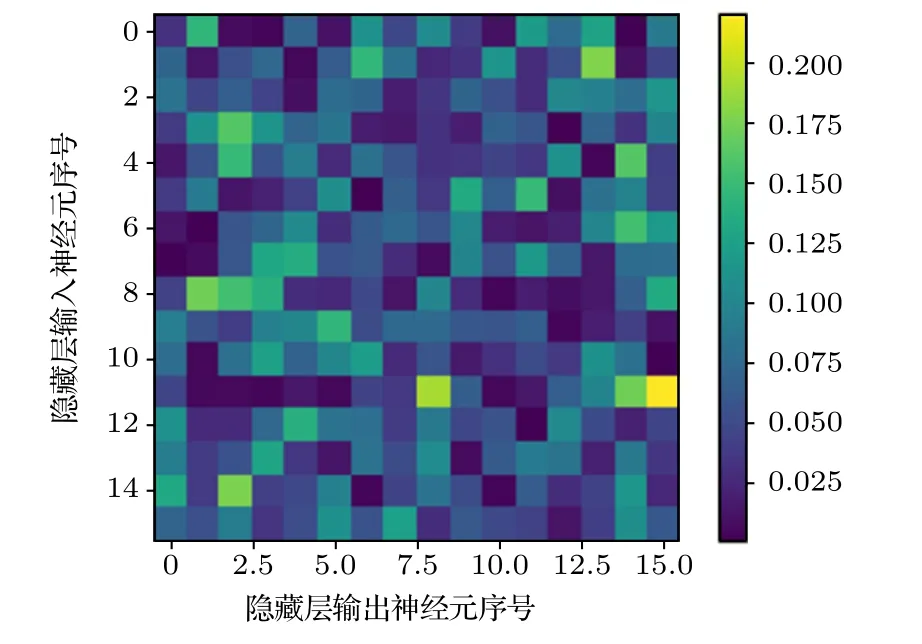
图3 隐藏层输入神经元对输出神经元的权重热图Fig.3.Heat map of weight of input neuron to output neuron in hidden layer.

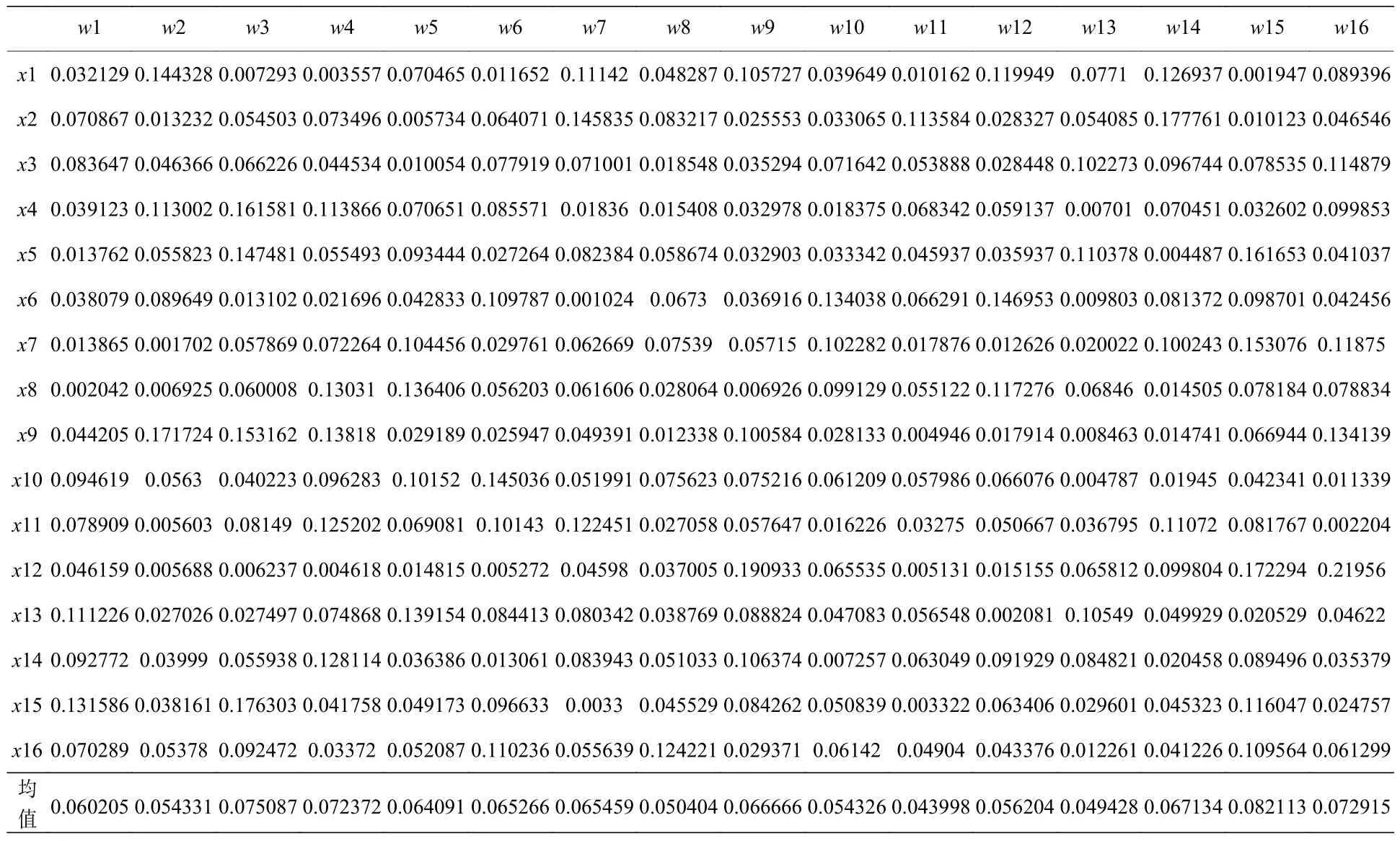
表3 输出门权重矩阵图Table 3.Heat diagram of output door’s weights.

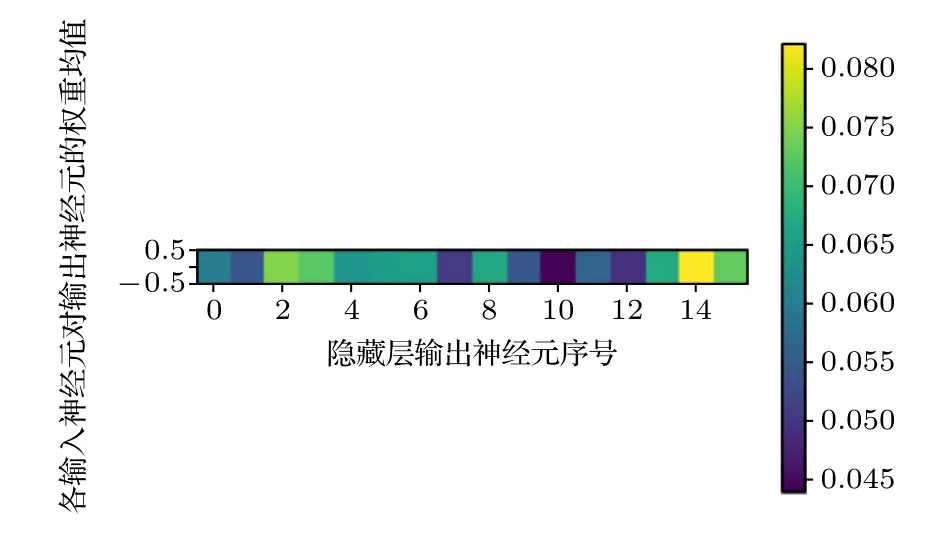
图4 隐藏层各输入神经元对输出神经元的权重均值热图Fig.4.Heat map of weights’ mean value of input neurons to output neurons in hidden layer.

输出神经元的计算公式

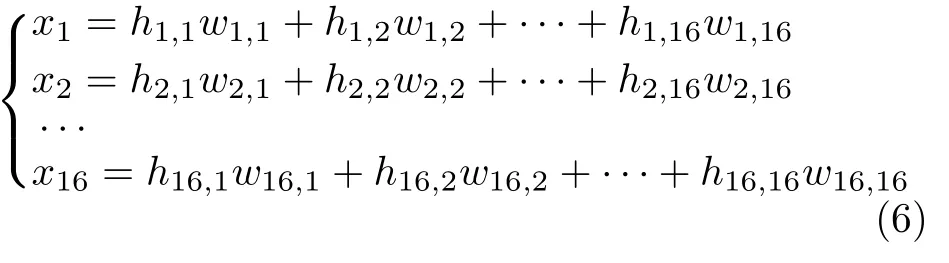
在以 2n为参数序列进行网格搜索[18-20]时,与16 个相邻的神经元参数为8,在该参数区间内,以不同阈值删减神经元并观察模型预测结果变化.图5 为16 个输入神经元的权重均值折线图,如w11列的权重均值在均值行中的颜色最浅,则该神经元对输出值的影响最小,w15 列的权重均值在均值行中的颜色最深,则该神经元对输出值的影响最大.

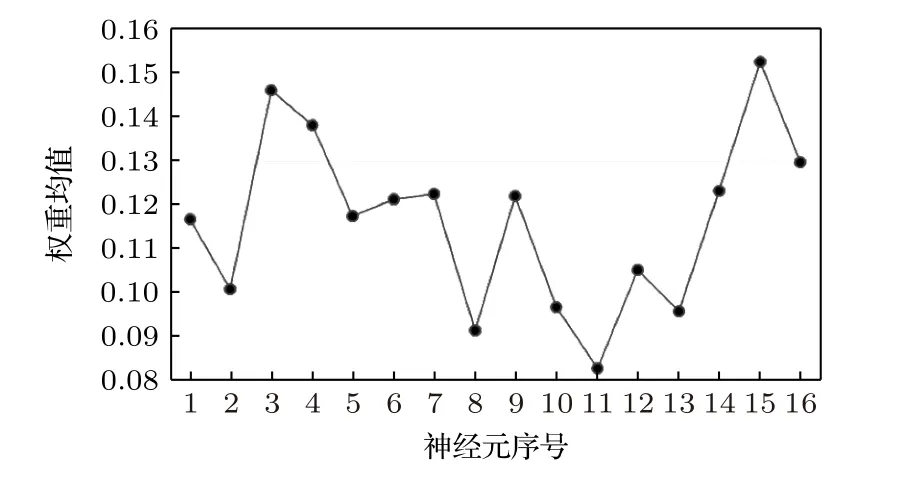
图5 权重均值折线图Fig.5.Line graph of the weights’ mean.

表4 给出以权重均值低于0.09,0.1和0.11 为阈值删除垃圾神经元以及神经元数调整前后的预测准确率,通过迷你趋势图观察以不同阈值删除垃圾神经元对模型预测性能的影响.通过网格搜索得到神经元数为16 时模型预测准确率为57.1%;权重均值低于0.09 的神经元有1 个,删除后神经元数降为15,预测准确率为59.3%,比初始结果提升2.2 个百分点;权重均值低于0.1 的神经元有4 个,删除后神经元数降为12,预测准确率为56.4%,比初始结果降低0.7 个百分点;权重均值低于0.11 的神经元有6 个,删除后神经元数降为10,预测准确率为51.4%,与初始降低5.7 个百分点.从预测准确率的迷你趋势图来看,删除1 个权重均值低于0.09 的垃圾神经元可提升预测效果,减少了部分过拟合;随着删减数目的增多,模型欠拟合,预测准确率逐渐低于原始水平.因此,基于权重分析适当删减垃圾神经元的方法能有效提升模型性能.

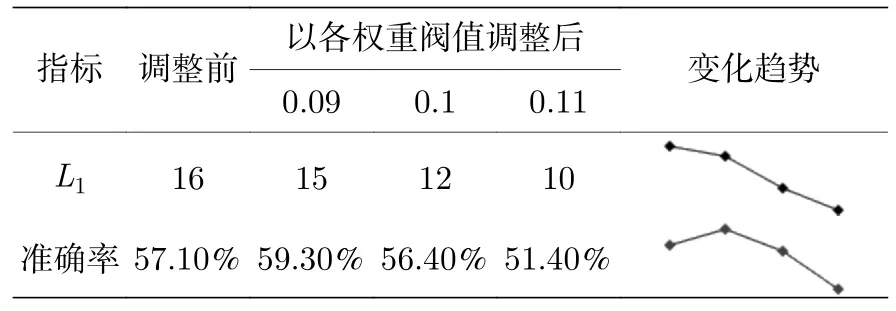
表4 µ=3.99 时不同参数的预测准确率Table 4.The prediction accuracy of different parameters when µ=3.99.

5 结果分析

三个系统在不同参数取值下,以相同策略选取删减垃圾神经元的权重阈值以提升最终的预测准确率;删除垃圾神经元的数量及调整网络结构前后的预测准确率具体结果如表5 所列.

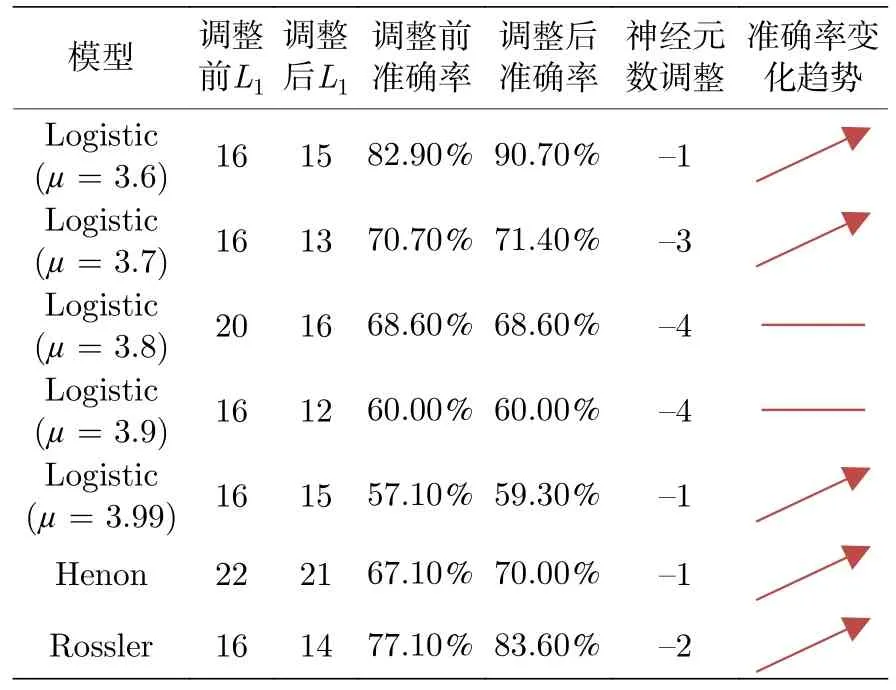
表5 神经元数及预测准确率变化表Table 5.Table of neuron numbers and prediction accuracy.

在Logistic 系统中,µ3.6 时的结果如表6 所列,网格搜索得到神经元数为16,模型预测准确率为82.9%.为使神经元数位于区间(8,16)中,分别以权重均值低于0.08,0.09,0.095 为阈值删减神经元并观察模型效果.删除权重均值低于0.08 的1 个神经元,预测准确率为90.7%,比初始预测结果提升7.8%;删除权重均值低于0.09 的4 个神经元,预测准确率为87.9%,比初始结果提升5%;删除权重均值低于0.095 的6 个神经元,预测准确率为78.6%,比初始结果降低4.3%,效果更差.从迷你趋势图来看,删除1 个权重均值在0.08 以下的垃圾神经元可最大程度提升预测效果;随着删减数目增多,运行成本持续降低,预测准确率逐渐回落,直至模型欠拟合使预测效果低于原始水平.

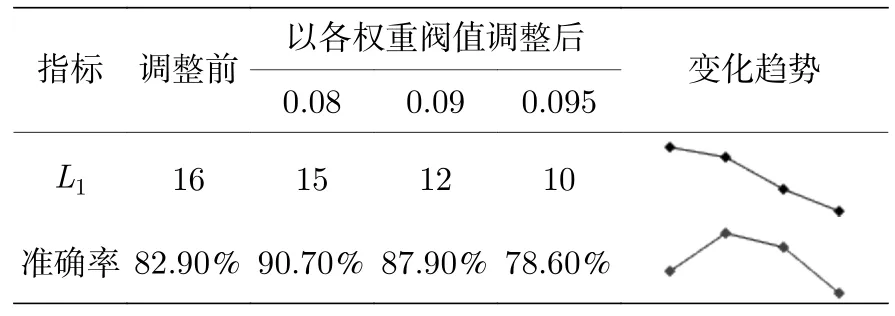
表6 µ=3.6 时不同参数的预测准确率Table 6.The prediction accuracy of different parameters when µ=3.6.

µ3.7 时的结果如表7 所列,网格搜索得到神经元数为16,模型预测准确率为70.7%.为使神经元数位于区间(8,16)中,分别以权重均值低于0.075,0.09,0.105 为阈值删减神经元并观察模型效果.删除权重均值低于0.08 的3 个神经元,预测准确率为71.4%,比初始预测结果提升0.7%;删除权重均值低于0.095 的5 个神经元,准确率为65%,比初始结果降低5.7%;删除权重均值低于0.105 的7 个神经元,预测准确率为60.7%,比初始结果降低10%,效果更差.从迷你趋势图来看,删除3 个权重均值在0.075 以下的垃圾神经元可最大程度提升预测效果;随着删减数目的增多,模型欠拟合导致预测效果愈发低于原始水平.

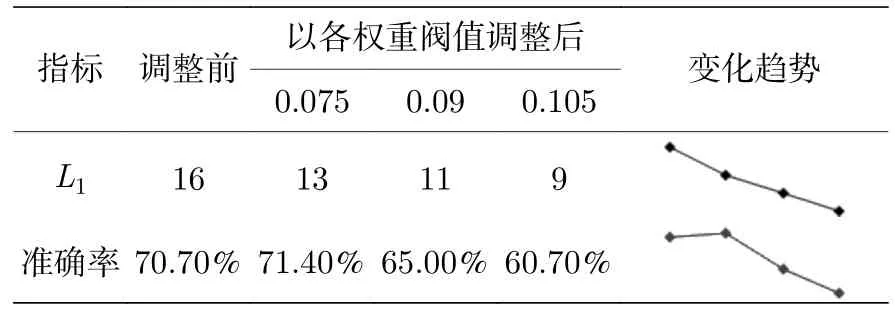
表7 µ=3.7 时不同参数的预测准确率Table 7.The prediction accuracy of different parameters when µ=3.7.

µ3.8 时的结果如表8 所列,网格搜索得到神经元数为20,模型预测准确率为68.6%.为使神经元数位于区间(10,20)中,分别以权重均值低于0.08,0.09,0.1 为阈值删减神经元并观察模型效果.删除权重均值低于0.08 的2 个神经元和权重均值低于0.095 的5 个神经元,预测准确率均为68.6%,均与初始结果持平,但删减数量越多,运行成本会相对越低;权重均值低于0.105 的神经元有8 个,删除后神经元数降为12,预测准确率为65%,比初始结果降低3.6%.从迷你趋势图来看,删除4 个权重均值在0.09 以下的垃圾神经元可在预测准确率不降低的前提下节省最多的运行成本;继续删减便会导致模型欠拟合,使得预测效果低于原始水平.

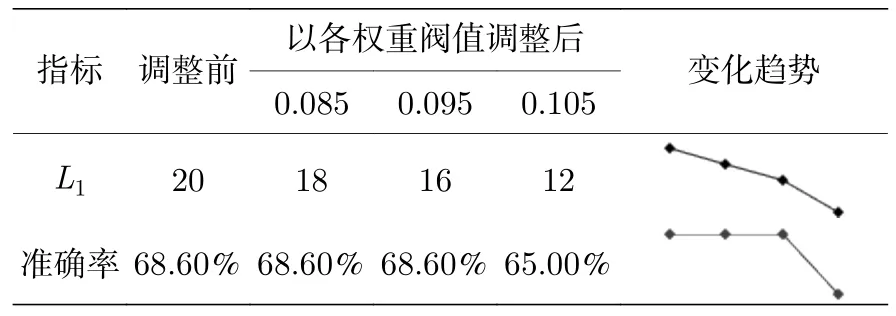
表8 µ=3.8 时不同参数的预测准确率Table 8.The prediction accuracy of different parameters when µ=3.8.

µ3.9 时的结果如表9 所列,网格搜索得到神经元数为16,模型预测准确率为60%.为使神经元数位于区间(8,16)中,分别以权重均值低于0.09,0.095,0.1 为阈值删减神经元并观察模型效果.删除权重均值低于0.09 的2 个神经元和权重均值低于0.095 的4 个神经元,预测准确率均为60%,均与初始结果持平,但删减数量越多,运行成本会相对越低;权重均值低于0.105 的神经元有6 个,删除后神经元数降为10,预测准确率为55%,比初始结果降低5%.从迷你趋势图来看,删除4 个权重均值在0.095 以下的垃圾神经元可在预测准确率不降低的前提下节省最多的运行成本;继续删减便会导致模型欠拟合,使得预测效果低于原始水平.

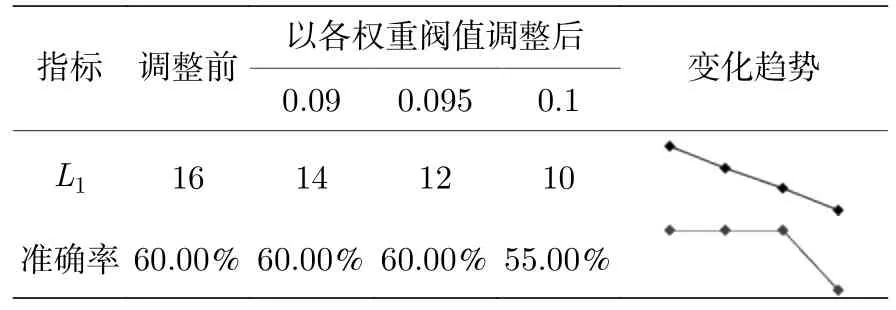
表9 µ=3.9 时不同参数的预测准确率Table 9.The prediction accuracy of different parameters when µ=3.9.

图6 给出参数µ分别取值3.6,3.7,3.8,3.9,3.99 时选择最优权重阈值的变化.µ值越小混沌程度越弱,µ值越大混沌程度越强,可见随着混沌程度的提升,最优权重阈值整体呈上升趋势;系统越混沌,需要保留的神经元权重越高.图7 给出参数µ分别取值3.6,3.7,3.8,3.9,3.99 时优化超参数前后的模型预测准确率变化.由于参数越大,模型的混沌程度越高,当µ接近4 时,x取值越近似于在0—1 之间随机分布,预测难度更大.因此整体来看,无论超参数调整前还是调整后的预测准确率都呈下降趋势;从调整超参数前后的预测准确率变化幅度来看,剔除垃圾神经元对模型性能的提升效果是逐步降低的.但最差的效果也就是预测准确率与原先持平,而运行成本却大大降低了,说明该方法可准确定位到对模型预测没有贡献的垃圾神经元,在不影响训练效果的情况下,最大程度降低模型运行负担、提升模型性能,这在参数众多、耗时较长的深度学习模型训练中是有重要意义的.

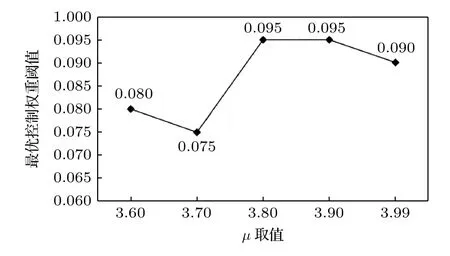
图6 不同混沌状态对应的最优权重阈值变化Fig.6.The change of optimal weight threshold corresponding to different chaotic states.

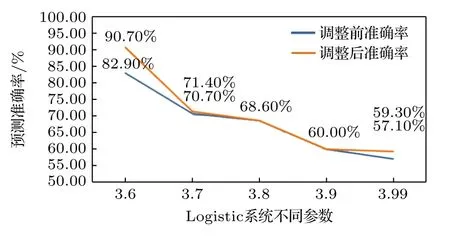
图7 不同混沌状态对应的预测准确率变化Fig.7.The change of prediction accuracy of different chaotic states.

为了进一步说明该方法的可行性,本文用Henon 系统和Rossler 系统的一维独立变量分别再次进行实证研究,结果如表10和表11 所列.

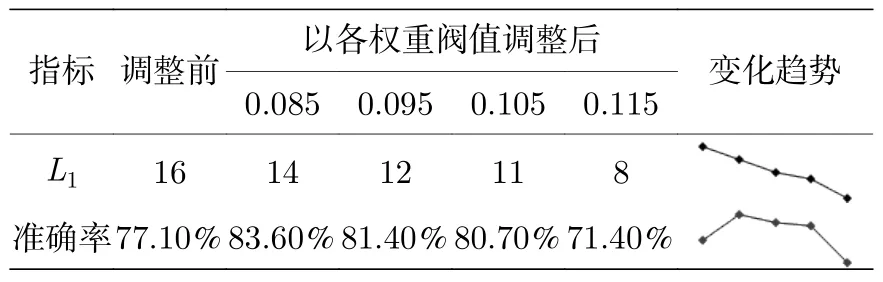
表11 Rossler 系统取不同参数的预测准确率Table 11.Prediction accuracy of Rossler system for different parameters.

在Henon 系统一维独立数据模型中,网格搜索得到神经元数为22,模型预测准确率为67.1%.为使神经元数位于区间(14,22)中,分别以权重均值低于0.1,0.11,0.12,0.14 为阈值删减神经元并观察模型效果.如表10 所列,删除权重均值低于0.1 的1 个神经元后,预测准确率为70%,比初始结果提升2.9%;删除权重均值低于0.11 的3 个神经元后,预测准确率为66.4%,比初始结果降低0.7%;删除权重均值低于0.12 的6 个神经元后,预测准确率为65.7%,比初始结果降低1.4%;删除权重均值低于0.14 的8 个神经元后,预测准确率为65%,比初始结果降低2.1%.从迷你趋势图来看,删除1 个权重均值在0.1 以下的垃圾神经元可最大程度提升预测效果;更多的删减则导致模型欠拟合,预测效果越来越差.

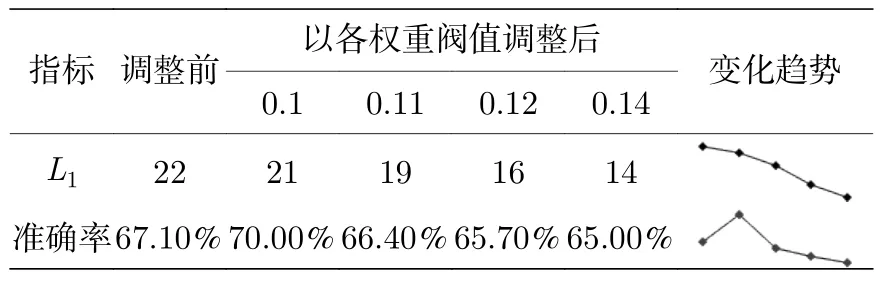
表10 Henon 系统取不同参数的预测准确率Table 10.Prediction accuracy of Henon system for different parameters.

在Rossler 系统一维独立数据模型中,网格搜索得到神经元数为16,模型预测准确率为77.1%.为使神经元数位于区间(8,16)中,分别以权重均值低于0.085,0.095,0.105,0.115 为阈值删减神经元并观察模型效果.如表11 所列,删除权重均值低于0.085 的2 个神经元后,预测准确率为83.6%,比初始结果提升6.5%;删除权重均值低于0.095的4 个神经元后,预测准确率为81.4%,比初始结果提升4.3%;删除权重均值低于0.105 的5 个神经元后,预测准确率为80.7%,比初始结果提升3.6%;删除权重均值低于0.115 的8 个神经元后,预测准确率为71.4%,比初始结果降低5.7%.从迷你趋势图来看,删除1 个权重均值在0.085 以下的垃圾神经元预测效果最好;以低于0.095和0.105 为阈值删减神经元带来的预测准确率提升相对前者越来越低,但仍然高于初始水平,且运行成本越来越低;继续删减更多的神经元,模型欠拟合导致预测效果越来越差,低于初始水平.

以上所有模型均采用滑动选取样本的方法,进行了10 次以上的训练并对最终的评价指标取平均值,故结果具有统计意义,并非偶然现象.观察这些系统在删减不同阈值下垃圾神经元时的预测效果变化,发现大多情况下,使预测效果提升最大的阈值不超过0.1,即通常将权重均值不超过0.1(甚至更低)的神经元视为垃圾神经元并删除可较大提升模型性能.通过多次实验,充分证明所提方法的可行性与有效性.

6 结论与展望

针对现有的超参数优化方法存在的过拟合、计算量庞大等问题,本文提出了通过分析权重含义定位冗余神经元,从而快速高效地精简网络结构、降低运行成本、提升训练效果的方法.

由于深度学习模型参数众多,挨个遍历所有参数动辄耗时长达数年,运行成本极高;否则又会跃过最佳参数,达不到最好的训练效果,即使达到最好的训练效果,也可能因为模型结构不够精简而导致过拟合,冗余神经元也会大大降低运行效率.通过Logistic 模型、Henon 模型、Rossler 模型的实证分析,证明此方法可大大提高寻找最优参数的效率,减少模型中冗余的神经元,从而避免过拟合、提高泛化能力.在模型预测准确率不受影响的前提下,有效缩短计算时间,提高运行效率,甚至可以通过减少过拟合使准确率得到提升.

混沌时间序列为看似无序的有序系统,以此进行实证研究可证明方法本身的有效性.但在实际数据中往往存在许多白噪声,因此,如何降噪并有效应用于实际数据成为我们下一步继续研究的问题.