Fe-C 合金在辐照条件下基体缺陷演化的OKMC 模拟*

沈子钦 艾德生 吕沙沙 高杰 赖文生 李正操‡

1)(清华大学,核能与新能源研究院,北京 100084)

2)(清华大学材料学院,先进材料教育部重点实验室,北京 100084)

3)(北京师范大学核科学与技术学院,射线束技术教育部重点实验室,北京 100875)

本文研究了Fe-C 合金中碳元素陷阱对基体缺陷的影响，以及在辐照条件下Fe-C 合金中基体缺陷的演化.通过将陷阱复合体参数化后进行实例动态蒙特卡罗(OKMC)建模，从而建立微观计算模拟数据与宏观实验数据之间映射的桥梁.模拟结果验证了碳(C)-空位(Vac)复合体在理想条件下的演化，在较低温度下，复合体主要为C-Vac2.基于复合体陷阱的假设，对Fe-C 系统中基体缺陷在辐照条件下的演化进行了模拟.验证了碳空位复合体对基体缺陷有明显的捕获作用.模拟Fe-C 系统中基体缺陷在辐照条件下的演化能够得到与实验一致的结果，对比讨论了模拟中使用的有效近似参数对模拟结果的影响，为铁基合金辐照缺陷演化的研究提供了基础支撑.

1 引言

反应堆中的中子辐照、高温、高压环境使铁基合金产生微观结构改变,韧脆转变温度升高,导致金属材料的力学性能发生劣化.早在20 世纪50 年代,对材料辐照效应的研究就已经发现辐照位错环和空洞等基体缺陷的产生是铁基合金脆化的一大机制[1-3],其他两大机制分别是溶质团簇析出[4]和晶界偏析[5].由于中子辐照条件及测试实验较为困难,采用计算机模拟研究核材料的辐照效应,分析辐照条件下微观组织的演化,评估推测材料辐照脆化等力学性能,是替代中子辐照实验一个可行方法.

材料晶体中的缺陷演化涉及非常复杂的动力学过程,如空位加强的溶质团簇扩散,其团簇的移动是空位在该溶质团簇表面一系列反复跃迁事件的结果.因此研究辐照诱导的晶体缺陷长期演化过程,需要将微观尺度的原子相互作用能计算、辐照级联碰撞模拟和介观尺度的动态蒙特卡罗(kinetic Monte Carlo,KMC)模拟、团簇动力学等模拟方法进行多尺度结合.其中实例动态蒙特卡罗方法(object kinetic Monte Carlo,OKMC),可以基于分子动力学(molecular dynamics,MD)、原子蒙特卡罗(atom kinetic Monte Carlo,AKMC)模拟的计算结果,通过对缺陷和相应物理过程参数的抽象和简化,跟踪并模拟系统非平衡态的动态演化过程,在更长时间跨度内研究缺陷的演化行为,从而建立起微观缺陷运动机制和宏观实验观测之间的桥梁.

本文采用OKMC 模拟,基于原子尺度的计算模拟研究结果,对缺陷(团簇)两个最主要的性质(移动性和稳定性)进行参数建模,分析碳-空位复合体对空位团簇演化的影响,并将其参数化,建立了完整的Fe-C 系统基体缺陷演化模型.利用该模型,本研究重复了一组与实验相对应的缺陷演化过程,验证了模型对缺陷演化预测的有效性.

2 Fe-C 模型实例化

2.1 OKMC 模拟算法

OKMC 算法假设系统在不同的状态之间随机转移,转移概率rij仅与前一个状态i和后一状态j有关,同时所有的转移概率也是在时间上独立的,是一个马尔科夫过程.这些转移概率即为蒙特卡罗算法的输入参数.本研究以阿伦尼乌斯公式计算这些转移概率[6]:

其中Eij为系统从i状态跃迁至j状态时的激活能,前置因子Pij为尝试频率,+Eb.即系统从低能量的i状态跃迁到高能量的j状态的激活能等于初态与末态形成能的差值加上跃迁过程中需要克服的势垒Eb,由于j态形成能高于i态,则相反的转移过程对应的激活能Eji=Eb.记系统处于i状态的性质为Si,在j状态的性质为Sj,则当系统演化处于平衡时.Si×rijSj×rji.假设尝试频率Pij=Pji,则系统在i态和j态性质之比为该比值与状态跃迁时的势垒无关,但跃迁势垒将决定系统演化的时间,因此OKMC 能够描述系统随时间的动态演化过程.

2.2 Fe-C 系统中缺陷的实例化假设和反应网络

Fe-C 中的基体缺陷在OKMC 模拟中被视作独立的实例,每一个实例拥有不同的性质参数,如尺寸、捕获半径、尝试频率、激活能和结合能等函数.除此之外,在bcc 铁中缺陷通常拥有两种可能的形状—球体(三维)或位错环(二维),其中空位团簇通常作为三维球体存在,而间隙原子团簇通常作为二维的位错环.所有的实体在一个给定的空间中按其物理规律离散化运动,如位错环的最小移动距离和方向是伯氏矢量的大小和方向.系统中的缺陷团簇在演化过程发生相互作用产生所谓的缺陷反应网络,并有相应的反应距离,当两个实例之间的距离小于他们各自的反应半径之和时,就可以发生反应.

图1 给出了Fe-C 基体缺陷演化模拟中所考虑的所有实例种类及部分反应网络,其中碳(C)、空位(Vac)和自间隙原子(SIA)为基本粒子,它们相互组合可以形成两类缺陷团簇,即空位型团簇(Vac-Cluster)和间隙型团簇(SIA-Cluster),其中也包括碳-空位复合体C-Vac2,该复合体进一步吸收空位可以形成团簇C-Vac3.间隙原子可以形成挤列子,如记号为SIA6的团簇为含有6 个间隙原子的挤列子,同时该挤列子所含间隙原子个数大于某一阈值时,可转变为〈111〉位错环.当两种类型的缺陷团簇在运动演化过程中相遇会发生缺陷反应,聚合为更大的缺陷团簇或者相互合并,如〈111〉位错环SIA6与Vac3合并后将形成SIA3挤列子.后文将对相应的参数进行详细说明,本研究在开源代码MMonCa[7]的框架内对上述缺陷和反应网络进行建模,在该框架下,反应半径的定义为其组成的粒子的捕获半径的叠加.

图1 OKMC 中的缺陷反应网络Fig.1.The networks of defects reaction in OKMC simulation.

2.3 缺陷团簇的实例化

OKMC 的建模过程实际上为对上述反应网络中的缺陷性质进行实例化,主要包含两方面的性质,即移动性质和稳定性.缺陷团簇的性质是其尺寸的函数,为了建立这些参数函数,我们收集了其他研究者通过第一性原理计算和分子动力学计算给出的数据.下面将分别阐述这些缺陷实例的参数选择.

空位团簇的移动性: 在MMonCa 中的团簇移动性由扩散系数定义,而扩散系数的微观定义为[8]

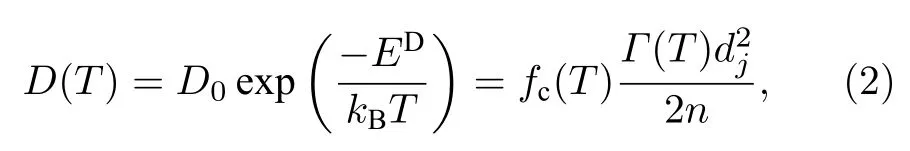
其中,D0是扩散的前置因子,ED是扩散激活能.fc是与温度有关的相关因子,为随机行走相关性的度量.dj是缺陷一次跃迁的距离,在本研究中为0.287 nm.n为该缺陷运动的维度,当缺陷为三维随机游走时取值为3,当缺陷为一维随机游走时取值为1,如〈111〉位错环.Γ(T)为跃迁频率[8]:

其中是移动尝试频率,在本研究中假设缺陷扩散为完全随机行走,则fc近似于1,约等于ED.对单个空位,通过密度泛函理论(DFT)计算得到该移动激活能为0.64 eV[9]和0.67 eV[10],通过实验方,通过实验方法测定的值为0.55—0.57 eV[11],而通过经典Mendel,而通过经典Mendelev 势计算得到的值为0.63 eV[12],本研究将单空位的移动激活能设置为=0.63 eV,该值介于上述理论计=0.63 eV,该值介于上述理论计算和实验测定值之间,较为可靠.同时我们使用Debye 频率作为跃迁的尝试频率,即v1=6×1012s—1.对于含有Nv个空位的空位型团簇,当Nv=2—10 时,本研究使用AKMC 的模拟计算结果[13]作为其移动激活能和跃迁尝试频率,这些计算表明,双空位的移动激活能与单空位接近,而三空位团簇则比单空位更容易扩散.而对于Nv＞ 10 的空位型团簇,其移动激活能的模拟计算值在1.15—1.50 eV之间浮动,因此本研究选择了一个中间值,将其移动激活能设置为1.30 eV,并假设相应的移动扩散机制为表面扩散机制[14,15],即这些空位团簇的移动为一系列表面空位跃迁事件的结果,相应的跃迁尝试频率由下式可以计算得到:

空位团簇的稳定性: 在定义空位团簇的稳定性之前,需要先定义空位团簇的形成能,在MMonCa 中团簇形成能的定义为其组成粒子的形成能之和减去这些粒子组成团簇的势能:

其中Efor(V)为单空位在基体中的形成能,根据AKMC 的计算值,本研究将其设置为2.02 eV.Epot(Vn)为每一单空位结合到此团簇的结合能的累加:

其中Ebind()为单空位与含有Nv=n-1 个空位的团簇的结合能.经过AKMC 的计算模拟发现,团簇的构型在演化过程中也会发生改变,因此由此估算的结合能值略低于Mendelev 势和DFT 的计算值,事实上这可以解释为团簇解离的构型熵效应[13],因因此本研究中对Nv=2—4 的空位团簇的结合能取用了相应的AKMC 计算结果.而对于Nv＞ 4 的空位团簇的结合能,本研究也采用了文献中的拟合函数[13]:

从而可以定义空位团簇的稳定性,即空位团簇分解的速率,因为空位团簇发射出另一个空位团簇为极小概率事件[16],所以空位团簇的分解的主要方式为不断向基体中发射单空位.解离出单空位的激活能为该空位对原团簇的结合能与单空位的移动激活能之和:

单空位从团簇中解离的移动激活能等于单空位在基体中的移动激活能0.63 eV,该值与空位团簇的尺寸Nv无关.另外团簇的解离尝试频率应与团簇的尺寸成正比,这也是团簇吸收和发射点缺陷能达到平衡的条件,本研究中选择的尝试频率为:

间隙型团簇的移动性: 间隙型团簇的移动性定义的方法与团簇型缺陷类似,扩散前置因子同样由(2)式—(4)式确定.对于尺寸Ni＜ 5 的间隙型团簇,本研究中使用的缺陷跃迁激活能和跃迁尝试频率为基于Mendelev’s 势的分子动力学研究[17,18]和实验研究[19]的结果.需要说明的是,当间隙原子缺陷团簇长大到超过某一阈值时,将转变为〈111〉缺陷,本研究选择Ni=5 为挤列子转变为〈111〉位错环的阈值.同时,在模拟位错环运动时并未区分〈111〉位错环及〈100〉位错环,因此使用了一个有效的移动激活能,并设定了一个位错环的区分阈值Nth,即当位错环的中间隙原子个数介于5—Nth之间时,假设其中只有部分的〈100〉位错环,因此对尺寸位于该区间的位错环,将使用有效移动激活能,当位错环的原子个数大于Nth时,假设〈111〉位错环都转变为了移动激活能较高的〈100〉位错环,相应的移动激活能为0.90 eV,需要说明的是,在Jansson 等的模拟中,使用了Nth=90 作为该转变阈值,相应的有效移动激活能为0.2 eV,因此本研究对于这两个有效参数的设定首先选定了这两个数值,而在验证模型后也将对有效参数进行对比讨论.另外模拟中判定可观测位错环的原子个数阈值为90.对可观测位错环,其移动激活能通过分子动力学计算得到,但该值显著低于实验值1.30 eV[20],原因是在运动过程中被杂质陷阱钉扎导致跃迁频率下降,使其有效扩散激活能增加.对于Ni＞ 4 的间隙型团簇,其跃迁尝试频率由下式计算:

其中为了使Ni=5 的间隙团簇的跃迁尝试频率与文献结果一致,取值为c=8.11×1012s—1.其中Ni的指数部分e理论上从0.50—1.00 变化,分别对应于间隙原子扩散的独立挤列子模型[21]和位错环边缘的扭结移动模型[22].本研究中取值为e=0.75.

间隙型团簇的稳定性: 与团簇型缺陷的稳定性定义相似,间隙型团簇的分解激活能Edis(INi)是其发射点缺陷对团簇的结合能和移动激活能之和,对于单个间隙原子对团簇的结合能,采用Domain等main等[15]给出的拟合表达式:

2.4 陷阱复合体的实例化

影响实体扩散系数的一个重要因素是陷阱元素,如C,N等[23].从第一性原理和分子动力学的研究中发现,这些原子对间隙原子尤其是空位有较强的结合能,阻碍基体缺陷的迁移或抑制缺陷团簇中点缺陷的发射.

Jasson等[8]的研究表明,在较高温度下(563 K),碳-空位复合体的主要存在形式是C2-Vac,而在室温下其主要存在形式为C-Vac2,事实上分子动力学的计算结果也表明C2-Vac 及C-Vac2非常稳定,尤其是C2-Vac 在700 K 左右依然保持稳定,并且也有相应的实验已经证明了这些碳-空位复合体的存在[24].因此我们将复合体定义为实体粒子,相应的形成能与所对应复合体相同.在此基础上,即可定义复合体陷阱对空位团簇和间隙型团簇的结合能.陷阱粒子对间隙型团簇(位错环)的结合能取值参考自Anento和Serrad[25]的分子动力学研究成果,该研究发现根据陷阱对间隙型团簇(位错环)的捕获位置不同,相应的结合能也不同,如CVac2复合体位于〈111〉中心位置时,结合能约为1.40 eV,而位于边缘位置时结合能相对较弱,约为0.40 eV.C2-Vac 陷阱的对间隙型团簇的结合能则相反,陷阱位于间隙型团簇(位错环)的边缘位置时,结合能很强,约为1.20—1.40 eV,而位于间隙型团簇(位错环)的中心位置时结合能较弱,约为0.60 eV.

综上所述,由于单间隙或者双间隙缺陷团簇有很高的概率可以消去碳-空位陷阱中结合的空位,因此对于小尺寸的间隙型团簇与陷阱粒子的结合能有效值都较小.同样考虑到当陷阱位于位错环边缘位置时,陷阱中的空位有较大概率被消去从而失去强捕获效果.因此本研究对于包含Ni=5—30 个间隙原子的位错环,C-Vac2陷阱对其的结合能设为0.60 eV,而对于Ni＞30 个间隙子的位错环,认为其在运动过程中有更高的概率在中心处被捕获,因此相应的结合能为1.20 eV.另一方面,对高温(563 K)下主要的陷阱C2-Vac 而言,认为其对小尺寸间隙型团簇的结合能较弱,但对包含Ni=5—30 个间隙原子的位错环,其结合能设为1.40 eV,对Ni＞ 30 个间隙原子的位错环,出于与C-Vac2相同的考虑,结合能设为0.60 eV.另外,本研究中陷阱与间隙型团簇(位错环)的解离尝试频率与该团簇的移动尝试频率相同.

对于陷阱粒子对空位型缺陷的结合能取值来自文献[24],需要指出的是,陷阱除了捕获空位,同时也降低了小空位团簇的形成能,使之更加稳定,团簇发射单空位的尝试频率将下降,下降比率由下式确定[26]:

其中Et(trap,Nv)为陷阱对空位团簇的结合能.对高温和低温下两种形式的碳-空位陷阱复合体,结合能都随着空位尺寸的增加从0.80 eV逐渐降低至0 eV,当空位团簇尺寸Nv＞ 15 时,认为碳元素对空位团簇发射单空位的尝试频率没有影响.

3 模拟结果

3.1 陷阱种类验证模拟

为了验证在上述假设和参数下建立的模型的可靠性,在Jasson 的模拟条件下重复了其模拟过程,即仅允许Vac2,C,C-Vac,C-Vac2,C2-Vac和C2-Vac2这六种碳-空位复合体存在,退火模拟温度为328 K,同时每一秒插入一个空位,累计插入单空位数目为碳原子数目的两倍.模拟在尺寸为250a0× 250a0× 250a0的模拟胞中进行,模拟结果如图2 所示.

图2 碳空位陷阱复合体种类及浓度随空位浓度的演化Fig.2.Evolution of carbon-vacancy complexes concentration with the increasing vacancy concentration.

图2 中的模拟温度略高于室温,可以发现,在该退火模拟条件下,碳元素的含量随着空位的不断增加而逐渐降低至0,而碳-空位复合体的数量在增加.在整个过程中C-Vac2增长速度最快,同时CVac 出现了先增加后减小的趋势,在这个过程中也同时出现了C2-Vac和C2-Vac2,但总体含量低于10%,在此温度下主要的碳-空位复合体为C-Vac2.产生这一结果的原因主要是C-Vac2和C-Vac 在此温度下都较为稳定,体系中首先是单个碳原子捕获单空位形成C-Vac,并继续捕获单空位形成CVac2.该模拟结果与Jasson 等的模拟结果基本一致,因此也可印证本研究所用模型的可靠性.

3.2 Fe-C 在辐照条件下基体缺陷演化

基于上述Fe-C 基体缺陷的参数模型,在体积为250a0× 250a0× 250a0的模拟胞中对辐照条件下的基体缺陷演化进行了模拟研究和验证,模拟条件与对比研究的实验条件相同,辐照损伤速率约为7× 10—7dpa/s,实验温度为343 K,陷阱浓度为100 appm.在此模拟中允许的缺陷类型为点缺陷、空位型团簇、间隙型团簇(位错环),同时这些缺陷在运动过程中会被陷阱捕获而形成被钉扎的空位团簇或被钉扎的位错环,最大缺陷团簇中所含有的间隙原子(空位)个数设定为5000.模拟中的中子辐照事件为随机在模拟胞不同位置插入一组包含空位和间隙原子的缺陷,时间间隔设为1 s,该组缺陷由分子动力学(MD)模拟产生,初级碰撞原子(PKA)能量为10 keV,通过20 次重复模拟得到用于抽取级联碰撞缺陷的数据集.

本研究主要通过对比缺陷团簇数密度及平均尺寸随辐照剂量dpa 的变化,对缺陷演化过程进行描述,其中缺陷团簇平均尺寸是该种类缺陷团簇所含有的“基本粒子”总数与该种类缺陷总数的比值,以空位团簇为例,空位团簇平均尺寸为模拟中组成所有空位团簇的“基本粒子”总数与空位团簇总数目之比.另外由于OKMC 模型的假设简化了缺陷团簇的内部结构,将这个缺陷团簇视为一个抽象的“基本粒子”集合对象,因此只要该对象含有的“基本粒子”个数大于2 即被视为缺陷团簇.而对于间隙型团簇,为了便于与相应的实验结果进行比较,我们设定了相应的观测阈值,即大于该阈值的团簇才进行统计.需要说明的是,虽然有实验测定了0.5 nm 大小的位错环,对应的位错环含有的间隙原子个数约为20 个间隙原子左右,但本研究中设定的可观测位错环尺寸阈值为90 个间隙原子.

图3 给出了空位团簇和间隙型位错环的平均数密度随辐照剂量的演化,该结果与Zinkle和Singh[27]的实验能较为合,在该实验条件下,实验可观测到的位错环在辐照损伤约0.003 dpa 左右出现,并且空位团簇和间隙型团簇的平均数密度随着辐照剂量的增加而增加,同时可观察到间隙型位错环的增长速率快于空位型团簇,当辐照累积剂量达到0.2 dpa 时,空位团簇数密度比间隙型团簇数密度高大约一个数量级.

图3 (a)空位团簇数密度和(b)位错环数密度随辐照损伤剂量的演化Fig.3.Evolution of number density of (a)vacancy clusters and (b)SIA loops with the increasing dpa.

在该实验条件下,空位的移动性较弱,同时由于碳-空位复合体的形核效应,因此空位团簇的平均尺寸在10 个空位以下,如图4(a)所示.模拟可观测位错环的平均尺寸随辐照损伤剂量增加的趋势不明显,平均尺寸在200 个间隙原子左右,如图4(b)所示,这与位错环在该温度下的生长方式有关,在该温度下可观测位错环的移动性较弱,因此长大方式主要以吸收间隙原子或者小型间隙原子团簇为主.

图4 (a)空位团簇平均尺寸和(b)位错环平均尺寸随辐照损伤剂量的演化Fig.4.Evolution of (a)mean size of vacancy clusters and (b)SIA loops with the increasing dpa.

基于上述模拟模型,研究了不同温度对基体缺陷团簇形成演化的影响.在模拟过程中采用尺寸为250a0×250a0×250a0的模拟胞,模拟温度为343和563 K,辐照剂量为0.1 dpa.模拟完成后分别统计了实验可见的位错环数密度和空位团簇的数密度.

如图5 所示,在563 K 下,空位团簇的数密度在损伤剂量0.1 dpa 时大约为1×1023/m3,较343 K下降了一个数量级,并随着辐照剂量的累积有逐渐下降的趋势.对于563 K 下实验可见的间隙型团簇(位错环),其数密度约为1×1022/m3,同样在损伤剂量0.1 dpa 时,较343 K 下的缺陷团簇数密度降低了一个数量级.需要指出的是,在563 K 的模拟条件下,模拟中使用的陷阱种类为C2-Vac,而343 K 时使用的陷阱种类为C-Vac2,因此在563 K下缺陷团簇数密度的下降原因: 1)在高温下缺陷的移动能力增强,空位型团簇和间隙型团簇的复合作用增强;2)由于陷阱数量的下降,对位错环的钉扎作用减弱,进一步增强了缺陷间的复合作用.

图5 (a)位错环数密度和(b)空位团簇数密度在343和563 K 下随dpa 的演化Fig.5.Evolution of mean size of (a)SIA loops and (b)vacancy cluster with the increasing dpa at 343 and 563 K.

4 参数讨论

4.1 可见位错环阈值选择对基体缺陷演化的影响

图6 给出了563 K 下不同转变阈值Nth所对应的基体缺陷的演化,当转变阈值降低时,相应的可见位错环的数密度有所上升,而平均尺寸有所下降,说明位错环有效移动性的降低使得基体中的位错环合并作用减弱,但对于空位型缺陷,其团簇尺寸和数密度随着Nth的下降未见明显变化,由此可说明空位团簇本身的移动性较弱,与尺寸较大的位错环的复合效应在缺陷演化过程中不占主导地位.

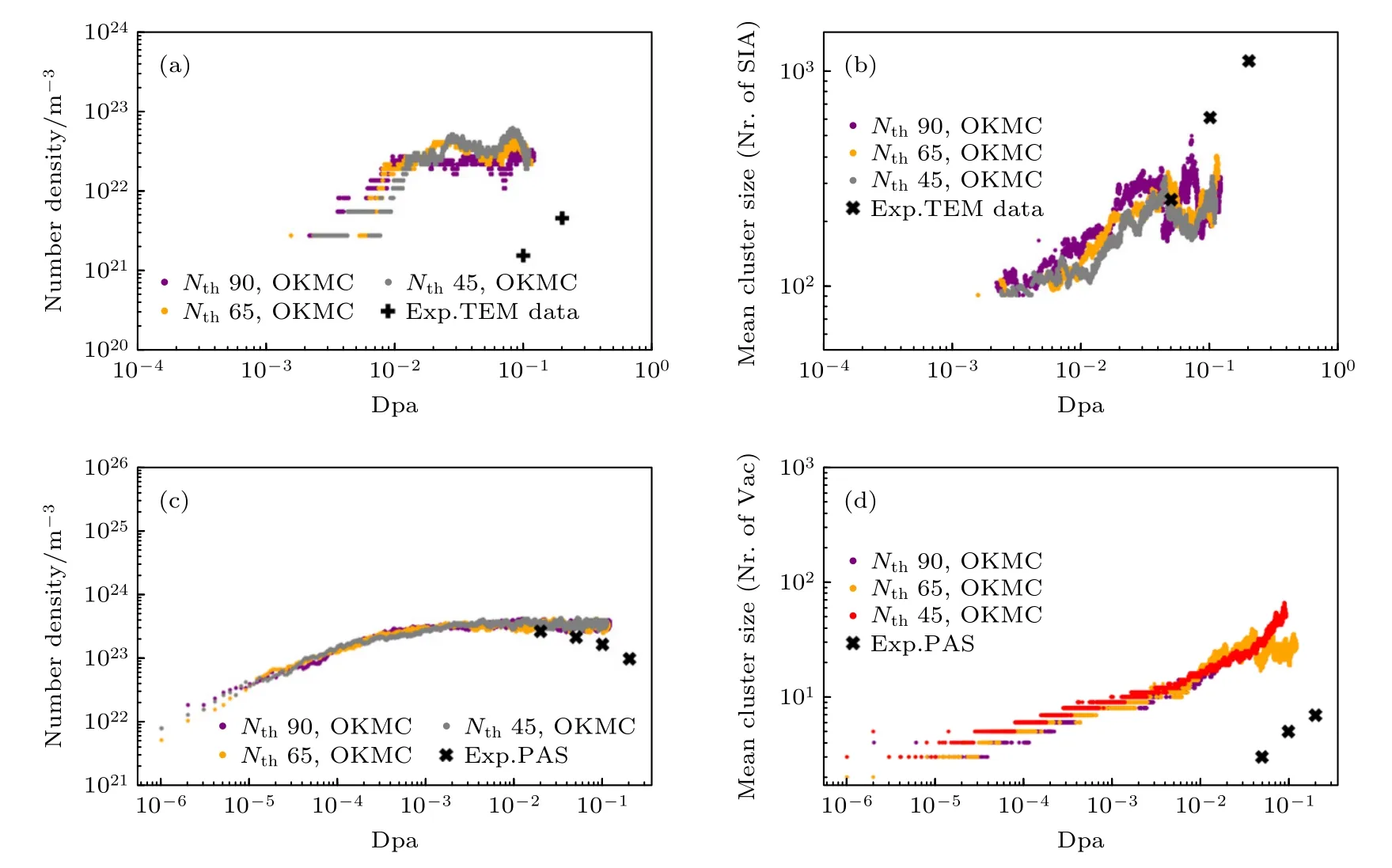
图6 位错环的(a)数密度和(b)平均尺寸以及空位团簇的(c)数密度和(d)平均尺寸在563 K 下随dpa 的演化Fig.6.Evolution of (a)SIA loops number density,(b)SIA loops mean size,(c)vacancy cluster number density,(d)vacancy cluster mean size density with the increasing dpa at 563 K.

4.2 位错环有效移动激活能对基体缺陷演化的影响

前文对比了不同转变阈值对基体缺陷演化的影响,发现尺寸较大的位错环的运动性质对空位型缺陷的演化影响并不显著,因此进一步研究了有效移动激活能对缺陷演化的影响,该参数对团簇尺寸为5—Nth的位错环运动性质有显著影响.如图7所示.当位错环的有效移动激活能增加时,实验可见的位错环的数密度和平均尺寸显著下降,并发现在本研究的模拟模型下,当有效移动激活能设定为0.40 eV 时,模拟数据与实验数据更为符合.但对于空位型团簇缺陷,尺寸为5—Nth的位错环的有效移动激活能变化对其演化的影响依然不显著,由此可以进一步推论,空位团簇与间隙团簇的复合效应主要是空位团簇与间隙原子挤列子(含有的间隙原子个数＜5)之间的复合.

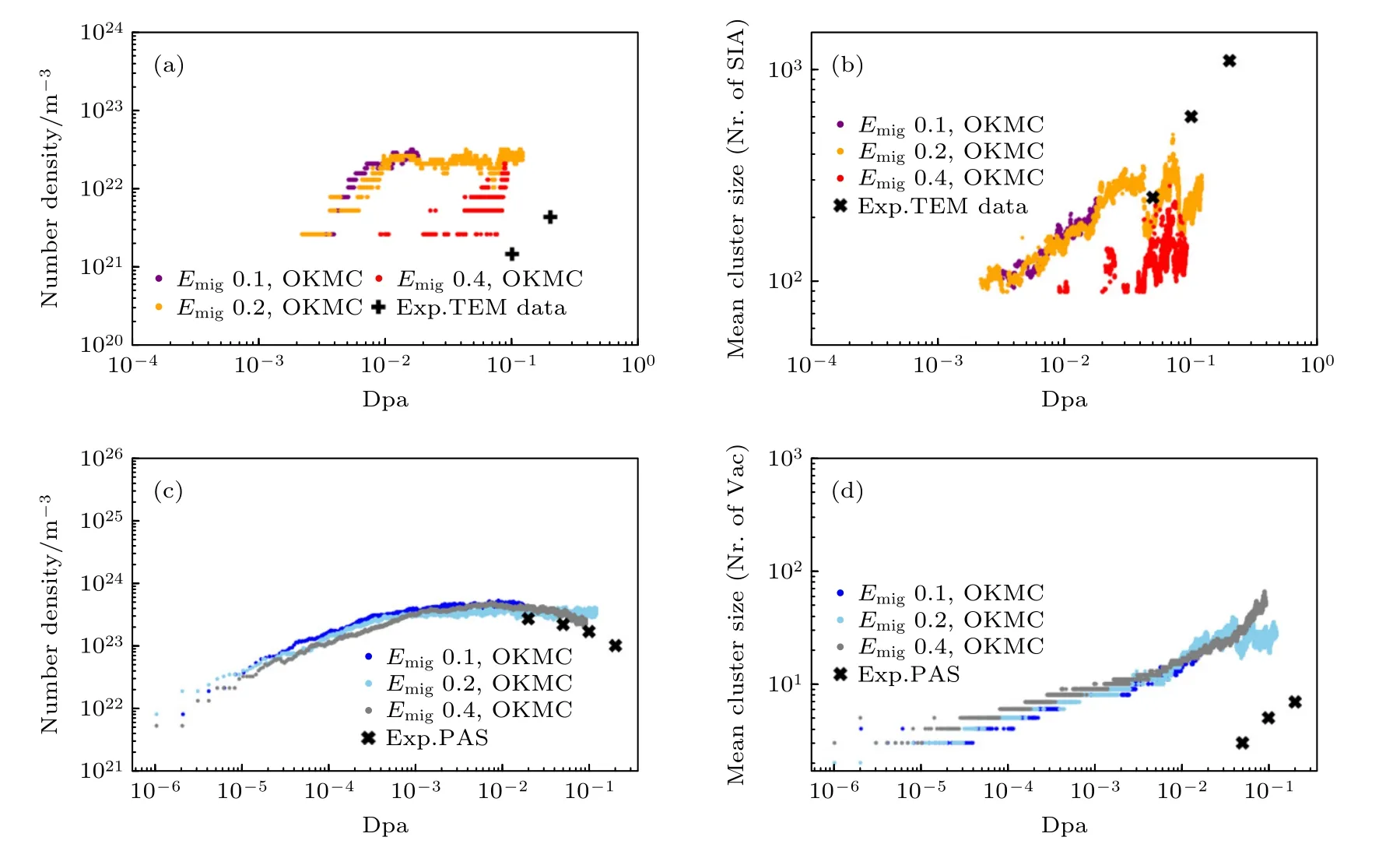
图7 位错环的(a)数密度和(b)平均尺寸以及空位团簇(c)数密度和(d)平均尺寸在563 K 下随dpa 的演化Fig.7.Evolution of (a)SIA loops number density,(b)SIA loops mean size,(c)vacancy cluster number density,(d)vacancy cluster mean size with the increasing dpa at 563 K.

4.3 碳-空位陷阱对空位团簇的捕获激活能对基体缺陷演化的影响

在本研究中碳-空位陷阱对空位的捕获也使用了一个有效的结合能数值,因此我们也对比了该有效结合能对空位团簇演化的影响,如图8 所示,随着结合能的增大,基体中空位团簇的数密度明显下降,同时团簇的平均尺寸增加.对于间隙型团簇,其数密度变化随该结合能的变化不显著,但值得注意的是,位错环的平均尺寸有随着该结合能降低而降低的趋势.显然,随着结合能的降低,小尺寸空位团簇的稳定性降低,基体中单空位的浓度增加,与间隙原子的复合效应增强,同时大尺寸的空位团簇和位错环吸收单空位的概率同时增高,因此出现空位团簇平均尺寸增加而位错环平均尺寸下降的趋势.

图8 位错环的(a)数密度和(b)平均尺寸以及空位团簇(c)数密度和(d)平均尺寸在563 K 下随dpa 的演化Fig.8.Evolution of (a)SIA loops number density,(b)SIA loops mean size,(c)vacancy cluster number density,(d)vacancy cluster mean size with the increasing dpa at 563 K.

综上所述,空位团簇和位错环在辐照条件的演化相互影响,空位团簇的生长方式主要是吸收单空位和间隙原子,碳-空位陷阱对空位的结合强度对空位团簇的形成和演化有明显的正相关性.另一方面,位错环主要是形核后通过吸收挤列子的方式长大,原因是挤列子的运动方式为三维运动,并且移动激活能也较小,具有很高的移动性,与位错环相遇的概率最高,而当挤列子转变为位错环之后,其运动方式由三维降低为一维,因此两个位错环相遇的概率远低于位错环与挤列子相遇的概率,因此位错环的生长对转变阈值并不敏感,但在本研究中,对尺寸小于转变阈值Nth的位错环,其有效移动激活能仍然对位错环的演化有明显影响,当取值为0.40 eV 时与实验结果最为接近.

5 结论

本文通过OKMC 方法研究了碳元素对空位团簇演化的影响,建立了完整的Fe-C 基体缺陷演化模型,并结合文献中的实验结果进行了验证模拟.研究发现,碳-空位的稳定复合体主要有CVac2和C2-Vac 两种,室温下C-Vac2为稳定复合体的主要种类,因此室温辐照条件下Fe-C 系统中的陷阱浓度比高温辐照条件下更高.基于该Fe-C 基体缺陷演化OKMC 模型,可以得到与实验数据相一致的模拟结果,验证了模型的有效性,该模型的参数假设可以为实验结果提供很好的解释.在此基础上,讨论了模拟中使用的有效近似参数,包括位错环转变阈值、位错环有效移动激活能、碳-空位陷阱对空位团簇的捕获激活能,并通过这些参数的讨论对辐照条件下基体缺陷的演化机制进行了探究.结果证实,影响Fe-C 的基体缺陷演化的主要机制是单空位和挤列子的扩散、复合以及被大团簇吸收,而团簇间的合并机制对缺陷演化的影响并不明显.该结果对于辐照条件下Fe-C 合金中基体缺陷的演化研究具有重要参考意义.