Magnetic properties of a mixed spin-3/2 and spin-2 Ising octahedral chain

Xiao-Chen Na(那小晨) Nan Si(司楠) Feng-Ge Zhang(张凤阁) and Wei Jiang(姜伟)

1School of Science,Shenyang University of Technology,Shenyang 110870,China

2School of Environmental and Chemical Engineering,Shenyang University of Technology,Shenyang 110870,China

3School of Electric Engineering,Shenyang University of Technology,Shenyang 110870,China

Keywords: octahedral chain,magnetization plateaus,hysteresis loops,blocking temperature

1. Introduction

At low temperatures,the magnetic and electronic behavior of some chains may exhibit dependence on the value of the spin.[1,2]This phenomenon has garnered tremendous attention as differing behaviors were demonstrated when compared to the bulk matter of the same element.[3,4]Specifically,the focus has been on one-dimensional (1D) magnetic spin chains with transition metal ions due to their inherent magnetic anisotropies and potential application for information storage at the molecular scale.[5–11]Galisovaet al.investigated the orthogonal-dimer chain using the classical transfermatrix approach.[12]The results suggested that various ground states lead to six-type magnetization depending on three exchange couplings.

Additionally, the ferromagnetic phase and frustrated ferrimagnetic phase have both been discovered. Based on the Markov property of the dilute Ising chain, Panov obtained an explicit expression for the probability of any finite sequence.[13]He pointed out that the disordered dilute Ising chain with the regular Markov chain, while the ordering gives rise to the irregular Markov chain. Fabrelliet al.investigated the spin-1 field-induced antiferromagnet using a combination of experimental and theoretical techniques and delimited the quasi-1D region using quantum Monte Carlo calculations.[14]Daset al.synthesized the 1D spin-chain compound Ca3Co2−xFexO6and examined its magnetic properties.Some of the low-spin Co3+ions were converted into Co2+ions or, occasionally, both spin states experienced crossover due to the Fe-doping levelx.[15]By employing the transfermatrix method, the ground state phase diagram of spin-1/2 orthogonal-dimer chains has been investigated.[16]Magnetic properties of the quasi-1D spin-1 diamond chain with singleion anisotropy have also been discussed. The ground state phases exhibited an interesting frustrated state,with the magnetization forming different plateaus.[17]With Monte Carlo simulations, the magnetic properties of the mixed spins-5/2 and 3/2 Ising octahedral chains were investigated.[18]The ground state phase diagrams were determined and the magnetization and magnetic susceptibilities were obtained for this system with several typical anisotropies. If the system is chosen to mixed spins with integer(2)and half-integer(3/2)spins,will the magnetic properties differ from those of only mixed spins with half-integer(5/2,3/2)spins? In this study,we adopt the octahedral chain illustrated in Fig. 1. The blue and purple balls represent the spin-3/2 and 2 magnetic atoms,respectively. The solid and dotted lines depict the nearest neighbor ferromagneticJ(<0) and ferrimagneticJ1(<0) exchange couplings,respectively. The mixed spin-3/2 and 2 Ising model is employed to introduce the octahedral chain, as this is one of the most effective models for solving one-,two-and threedimensional problems.[19–22]

To examine this model, an effective field theory (EFT)was employed to analyze the magnetism.[23–26]In our previous studies, we have successfully employed an EFT to study magnetic characteristics of nano-systems.[27–35]The purpose of this study is to investigate the magnetic properties of the octahedral chain described by the mixed spin Ising model based on the EFT.This method takes into account the correlation of spin itself and is therefore superior to mean field theory. In Section 2,the Hamiltonian and a phase transition formula are derived for an octahedral chain using the EFT.In Section 3,the magnetization plateaus, hysteresis loops, and phase diagrams are calculated,while the final section presents some concluding remarks.

2. Calculation method

An octahedral chain with two types of magnetic atoms is depicted in Fig.1. The initial spins of the blue balls along the magnetic field(h)are anti-parallel to those of the purple balls.The ferromagnetic exchange couplingJis set to unity(J=1).Using the EFT,the Hamiltonian for the octahedral chain is

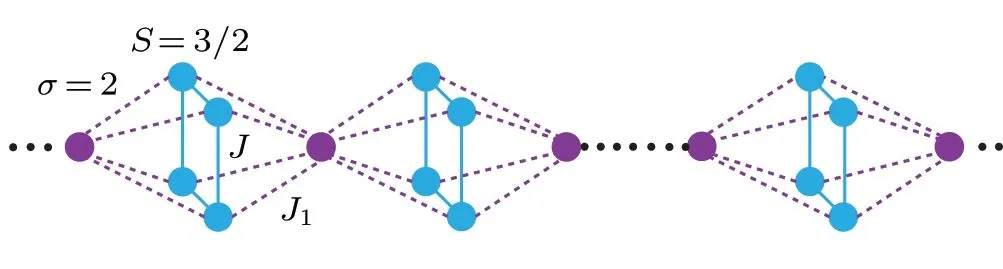
Fig.1. Schematic of the mixed spin octahedral chain.

3. Numerical results and discussion

In this section,some typical results based on the magnetic properties of the octahedral chain described by the ferrimagnetic mixed Ising model are investigated. Suppose that the spin-3/2 at the blue sites is parallel to the magnetic field (h),while the spin-2 at the purple sites is anti-parallel and the ferromagnetic exchange coupling is set to unity.

3.1. Magnetization plateaus and hysteresis loops of the octahedral chain

The step effects exhibited at low temperatures by the magnetization of the system with an increasing magnetic field are known as magnetization plateaus. Generally, the number of plateaus depends on the values of spin and other parameters. The effects of the exchange couplingJ1and anisotropiesD1andD2on the octahedral chain are examined in Figs.2–4 at a fixed temperature ofT=0.06. The solid,dashed,and dotdashed lines denote the total average(M),A(Ma)and B(Mb)sublattice magnetizations,respectively.

The magnetization versus the magnetic field for the octahedral chain withD1=−0.5,D2=−3.5 and various values ofJ1are depicted in Figs.2(a)and 2(b). In these figures,magnetization plateaus are observed at the curves. The critical magnetic fieldhcis defined as the smallest magnetic field required for the magnetization to transition from one plateau to another,while that of the last plateau is known as the saturated magnetic fieldhs. In Fig. 2(a), three magnetization plateaus are observed atM=6/5, 7/5, and 8/5 withJ1=−0.2, corresponding tohc1=6.26 andhs=13.36, respectively. The sublatticeMaremains constant for the spin 3/2 state,whileMbmoves from a 0 to a +2 spin state ashincreases. The magnetization plateaus are sensitive to sublattice plateaus, such asM=[4×(3/2)+0]/5=6/5. In Fig. 2(b), four magnetization plateaus are observed atM= 1, 6/5, 7/5, and 8/5 withJ1=−0.7, corresponding tohc1= 5.26,hc2= 12.26,andhs= 19.36, respectively. The spin ofMbmoves from a−1 to a +2 state ashincreases, which differs from the previous example. An additional plateau was observed due toM=[4×(3/2)+(−1)]/5=1. Comparing Fig. 2(a) and Fig.2(b),the values ofhcandhsfor the same plateau increase with the increasing|J1|.

Fig.2. Magnetization plateaus of the octahedral chain with various J1:(a)−0.2 and(b)−0.7.

The magnetization against magnetic field for the octahedral chain withJ1=−0.7 andD2=−3.5 for variousD1are presented in Figs. 3(a) and 3(b). In Fig. 3(a), four magnetization plateaus are observed atM=1, 6/5, 7/5, and 8/5 withD1=−1.5, corresponding tohc1=5.26,hc2=12.26,andhs=19.36, respectively. In Fig. 3(b), six magnetization plateaus are observed atM=−2/5, 2/5, 3/5, 6/5, 7/5, and 8/5 withD1=−4.5, corresponding tohc1=0.54,hc2=6.8,hc3=9.1,hc4=12.26,andhs=19.26,respectively. Interestingly,Mbis inverted from 1 to 0,whileMamoves from spin 1/2 to spin 3/2 athc3. This phenomenon arises due to the opposite directions of the initial spins of the two types of sublattices(MaandMb) owing to the ferrimagnetic exchange coupling(J1<0). To retain this ferrimagnetic exchange coupling,they must change simultaneously. That is,MaandMbsimultaneously move up and down, respectively. Comparing the two cases,the critical magnetic fields increase with the increasing|D1|for the same plateau under lower magnetic fields. However, the saturated magnetic fieldhsretains the same value.The corresponding plateaus are similar for both the cases,for example,M=(4×3/2−0)/5=6/5 for bothD1=−1.5 and−4.5.

Fig.3. Magnetization plateaus of the octahedral chain for various D1:(a)−1.5 and(b)−4.5.

The magnetization versus magnetic field for the octahedral chain withJ1=−0.7 andD1=−0.5 for various values ofD2is illustrated in Figs.4(a)and 4(b). In Fig.4(a),five magnetization plateaus are observed from five spin states,−2,−1,

Fig.4. Magnetization plateaus of the octahedral chain for various D2:(a)−1.5,(b)−3.5.

0,1,and 2 forMb.They are observed atM=4/5,5/5,6/5,7/5,and 8/5 forD2=−1.5,corresponding tohc1=4.4,hc2=7.26,hc3=10.26, andhs=13.26, respectively. In Fig. 4(b), four magnetization plateaus are observed atM=5/5,6/5,7/5,and 8/5 forD2=−3.5,corresponding tohc1=5.26,hc2=12.26,andhs=19.26,respectively. Comparing the two figures,one of the lowered plateaus is due to the absence of the−2 spin state inMb. The multi-spin states of the system are sensitive to various parameters, stronger anisotropy makes the system in a low spin state, whereas weaker one makes it in a high spin state. This results in a different number of magnetization plateaus.

Figures 5(a)–5(d)demonstrate the effect of the ferrimagnetic exchange couplingJ1on the magnetic hysteresis loops and the coercivity of the octahedral chain withD1=−0.5 andD2=−3.5 at a fixed temperatureT=0.06.With increasingh,the curve saturates atMs=8/5 in Fig.5(a),whereJ1=−0.2.The coercivity and the remanence areHc=2.16 andMr=6/5,respectively. To explain the origin of the overall hysteresis loops,the magnetic hysteresis loops of the sublattices are plotted in Fig. 5(b) with the same parameters.MaandMbexhibit different dependencies for various values ofh,which determines the shape of the overall hysteresis loop. They also account for the source ofMs= (4×3/2+2)/5 = 8/5. In Fig.5(c),whereJ1=−0.7,the coercivity and the remanence areHc=2.26 andMr=5/5, respectively. In comparison of the two cases,Hcis observed to increase when the absolute value ofJ1increased from 0.2 to 0.7. Additionally, the coercivityHcversusJ1in Fig. 5(d) further confirms the above result.

Fig. 5. Hysteresis loops of the octahedral chain for (a) J1 =−0.2, (b)J1 =−0.2 for the sublattices, (c)J1 =−0.7, and(d)the coercivity Hc versus J1.

Fig. 6. Hysteresis loops for (a) D2 =−3.5, D1 =−1.5 and −4.5, (b) D1 =−0.5, D2 =−1.5 and −3.5, and the coercivity Hc, and (c) the three-dimensional space(Hc,D2,D1)of the octahedral chain.

The graphs in Figs. 6(a)–6(c) explain the effects of the anisotropies on the magnetic hysteresis loops and the coercivity of the octahedral chain forJ1=−0.7 andT= 0.06.In Fig. 6(a), the coercivity and the remanence areHc=1.2 and 0.58,andMr=5/5 and 2/5 forD1=−1.5 and−4.5,respectively, for a fixed anisotropy ofD2=−3.5. Moreover,three loops are found on the curve whereD1=−4.5, which is due to all possible spin states appearing with the increasing magnetic field. In Fig. 6(b), the coercivity and the remanence areHc=2.26 and 4.56, andMr=5/5 and 4/5 forD2=−3.5 and−1.5, respectively, for a fixed anisotropy ofD1=−0.5.The steps are observed on the hysteresis loops due to all possible spin states appearing with the increasing magnetic field. The effects of the anisotropies on the coercivity in the three-dimensional space(Hc,D2,D1)of the octahedral chain are given in Fig. 6(c). The hysteresis loop and magnetization plateaus are mainly caused by the multi-spin states of 1D ferrimagnetic system due to the anisotropy,which may have potential applications in magnetic memory devices.

3.2. Magnetization and blocking temperature of the octahedral chain

The curves in Figs.7(a)–7(c)depict the effects of the ferrimagnetic exchangeJ1on the magnetizations and the susceptibility of the octahedral chain forD1=−0.5 andD2=−3.5.In Fig.7(a),the temperature dependence of the magnetization is plotted for some typical values ofJ1. The depressed saturation magnetization is observed on the curves labeledJ1=−0.4,as the thermal agitation releases the saturation magnetization from the frustration. In Fig.7(b),three saturation magnetizations(Ms)at zero temperature are detected atMs=6/5,5/5, and 4/5, which arise fromMs=(4×3/2−0)/5=6/5,(4×3/2−1)/5=5/5, and(4×3/2−2)/5=4/5. The saturation sublattice magnetization labeledJ1=−0.9,−0.7 at zero temperature showed smaller than the absolute value of the maximumMbdue to its released from the frustration through thermal agitation. In Fig. 7(c), the temperature dependence of the susceptibility of the octahedral chain is analyzed using the same parameters as shown in Fig. 7(a). The temperature at maximum susceptibility is defined as the blocking temperature (TB), and we observe that with increasing|J1|,TBalso increases. For example,Tc=2.35, 2.7, 3.7, 4.5, and 6.1 forJ1=−0.2,−0.4,−0.7,−0.9, and−1.2, respectively. The blocking temperature (TB) as a function of the ferrimagnetic exchange couplingJ1is presented in Fig.7(d)forD1=−0.5 andD2=2.5. It is observed thatTBdecreases with decreasing|J1|,which agrees with the previous analysis.

The curves in Figs. 8(a)–8(c) depict the effects of the anisotropyD1on the magnetization and the susceptibility of the octahedral chain forJ1=−0.7 andD2=−3.5. In Fig. 8(a), the temperature dependence of the magnetization of the system is given for some typical values ofD1. Two values ofMsare found on the total average magnetization atMs=5/5 and 2/5.The different types of magnetization curves are due to the different temperature dependences ofMaandMbin Fig.8(b). The saturation magnetizations areMs=3/2 and 1/2, and 0 and−1 forMaandMb, respectively. This originates from the different magnetic states induced by anisotropy changes. In Fig.8(c),the temperature dependence of the susceptibility of the octahedral chain is analyzed with the same parameters as shown in Fig. 8(a). The singular behavior is observed atTBon the curve, at which point the temperature increases with decreasing|D1|. For example,TB=3.4, 2.9,2.3,1.5,and 0.8 forD1=−0.8,−1.2,−1.5,−2.3,and−4.5,respectively.

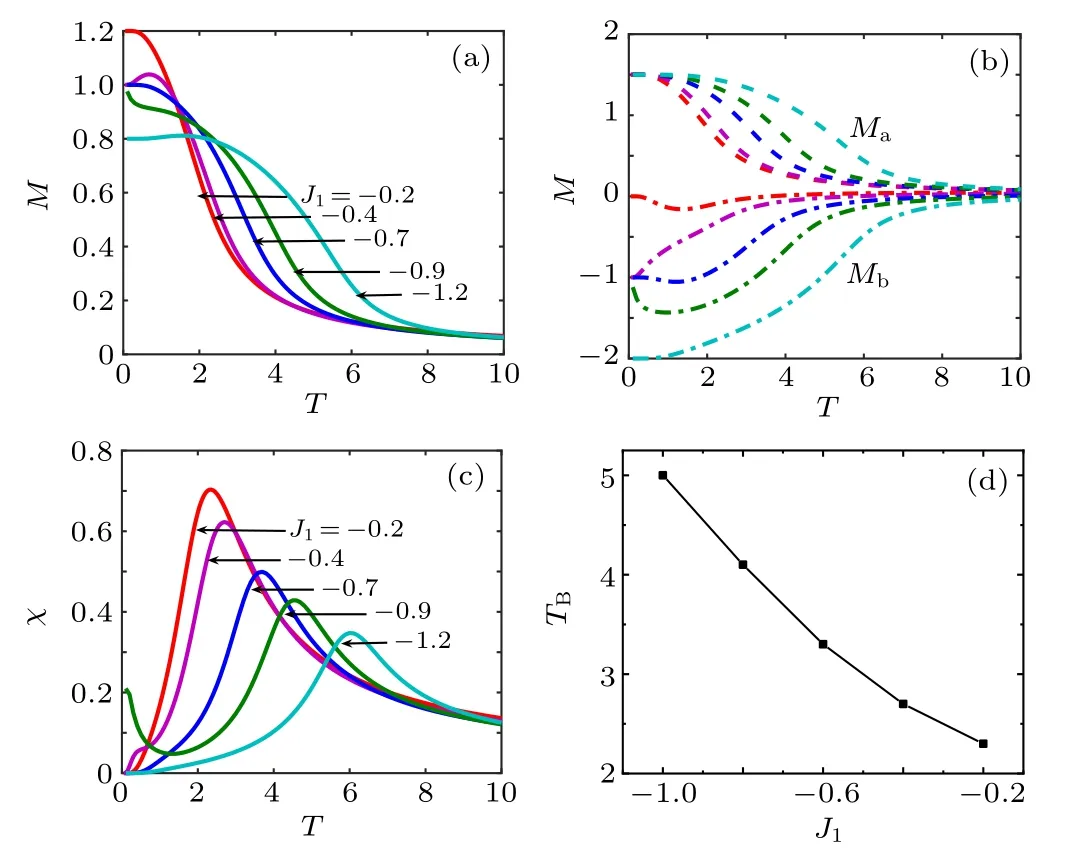
Fig.7. Temperature dependence of the(a)magnetization,(b)sublattice magnetization, (c) susceptibility, and (d) the blocking temperature TB vs. J1 of the octahedral chain for D1=−0.5,D2=−3.5.

The curves in Figs. 9(a)–9(c) describe the effects of the anisotropyD2on the magnetization and the susceptibility of the octahedral chain withJ1=−0.7 andD1=−0.5. In Fig.9(a),the temperature dependence of the magnetization of the system is plotted for some typical values ofD2.Two values ofMsare observed atMs=5/5 and 4/5. The different types of magnetization curves are due to the dependence of the various sublattice magnetizations on temperature,as illustrated in Fig.9(b).The saturation magnetizations areMs=3/2,and−2 and−1 forMaandMb,respectively. In Fig.9(c),the temperature dependence of the susceptibility of the octahedral chain is analyzed with the same parameters as shown in Fig. 9(a).The singular point on the curve atTBincreases with decreasing|D2|. For example,TB=3.7, 3.9, 4.1, 4.6, and 5.2 forD2=−3.5,−3.0,−2.5,−1.5, and−0.2, respectively. The susceptibility curve also contains an additional peak at low temperature due to the depressed saturation magnetization.The effects of the anisotropies on the blocking temperature are plotted in Figs.9(d)and 9(e)forJ1=−0.7. In Fig.9(d),the blocking temperature dependence of the anisotropyD1of the system is plotted for some typical values ofD2. For the same parameters,TBagrees with that obtained in Fig.9(c). To clearly show the variation of the blocking temperature with anisotropy,a three-dimensional space(TB,D1,D2)is provided for the octahedral chain.

Fig. 8. Temperature dependence of (a) magnetization, (b) sublattice magnetization, and (c) susceptibility for the octahedral chain with J1 =−0.7 and D2=−3.5. The number on the curve is the anisotropy D1.

Fig.9. Temperature dependence of(a)magnetization,(b)sublattice magnetization,and(c)susceptibility with J1 =−0.7 and D1 =−0.5,and the blocking temperature in(d)two-dimensional(TB,D1)and(e)three-dimensional space(TB,D1,D2)for the octahedral chain.

4. Conclusions

An octahedral chain described using a mixed spin Ising model has been investigated within the framework of an EFT with correlations. The calculations demonstrate that the exchange coupling and anisotropy exhibit important impacts on magnetism. For appropriate parameters, depressed saturation magnetization may be obtained in such a system.Furthermore,unusual behaviors, such as multiple hysteresis loops with the step effect and magnetization plateau inversion,have been discovered. These behaviors in 1D materials may be applicable to spin devices in the future.

Acknowledgements

Project supported by National Natural Science Foundation of China (Grant No. 51920105011) and the Key R&D Program of Liaoning Province of China (Grant No.2020JH2/10300079).