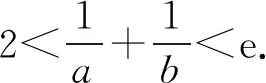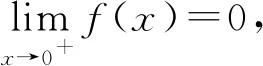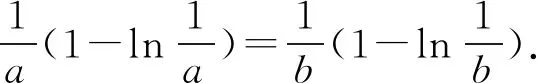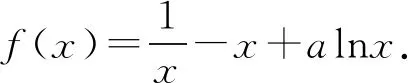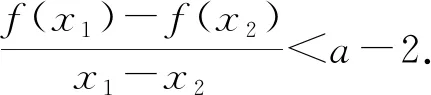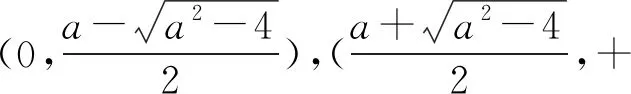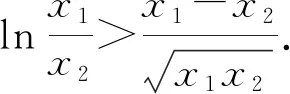2022年全国甲卷导数题的多解、变式与溯源
2022-08-30李武学
张 君 李武学
(四川省温江中学 611130)
1 试题呈现
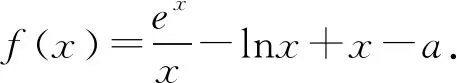
(1)若f(x)≥0,求a的取值范围;
(2)若f(x)有两个零点x1,x2,求证:x1x2<1.
2 试题分析
这道题综合考查利用导数研究函数的最值,再利用单调性与极值求给定条件下参数的取值范围,在此基础上研究两个零点之间的关系,是典型的极值点偏移问题.试题起点较低,绝大多数学生都可以拿分,但落点很高,第二问难度大,需要考生熟练掌握函数的有关性质,以及研究有关性质的基本方法和工具,并达到灵活运用的程度.对数学思想方法的考查也占很大成份,特别是对分类计论思想和转化思想的要求很高,只会死记硬背、按套路做题不会变通的考生是做不下去的.
极值点偏移问题的解题大方向主要有两个:构造对称函数和减少变量转化为一元函数问题.
3 解法探究
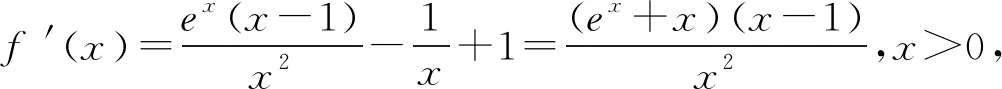
故a的取值范围为(-∞,e+1].
(2)由(1)知f(x)有两个零点的条件是a>e+1,且在(0,1)和(1,+∞)内各有一个零点,不妨设0 所以h(x)在(1,+∞)内单调递减. 则h(x) 所以g′(x)<0. 则g(x)在(1,+∞)内单调递减. 所以x1x2<1. 下面证明:当x>1时,ex>ex. 设s(x)=ex-ex,x>1,则s′(x)=ex-e>0. 所以s(x)在(1,+∞)内单调递增. 故s(x)>s(1)=0,ex>ex得证. 所以g′(x)<0. 则g(x)在(1,+∞)内单调递减. 以下同解法1. 方法3(利用同构化简,再构造函数) 设k(x)=x-lnx,则k(x1)=k(x2). 所以m(x)在(1,+∞)内单调递减. 故m(x) 所以x1x2<1. 方法4(减元法)由方法3,得 x1-lnx1=x2-lnx2. 所以g(t)在(1,+∞)内单调递减. 则g(t) 所以x1x2<1. 方法5(利用同构化简,再利用对数平均不等式转化为一元函数问题)f(x)有两个零点x1,x2,则e+1-a<0,得a>e+1.不妨设0 即ex1-lnx1+x1-lnx1=ex2-lnx2+x2-lnx2. 由于函数y=et+t在[1,+∞)上单调递增, 所以x1-lnx1=x2-lnx2. 即x2-x1=lnx2-lnx1. 下面证明:(对数平均不等式) 所以f(t)在(1,+∞)上单调递减. 故f(t) 所以x1x2<1. 问题等价于证明: 所以h(t)在(1,+∞)上单调递增. 所以h(t)>h(1)=0,问题得证. 溯源1(2021年新高考Ⅰ卷)已知函数f(x)=x(1-lnx). (1)讨论f(x)的单调性; 分析(1)f(x)的单调增区间为(0,1),单调减区间为(1,+∞). 由blna-alnb=a-b,得 则问题等价于证明:2 通过构造函数g(x)=f(2-x)-f(x)(0 本题属于典型的极值点偏移问题,构造函数即可证明. (1)讨论f(x)的单调性; 不妨设x1

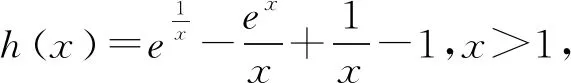
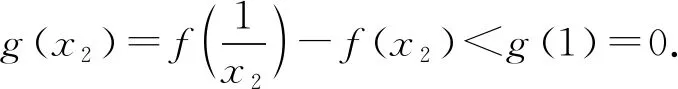



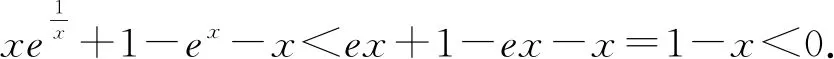
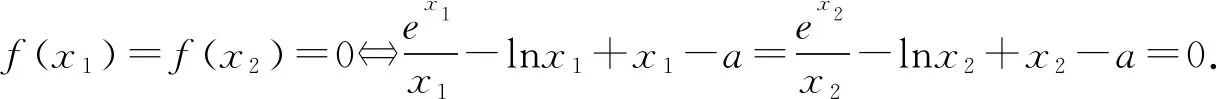

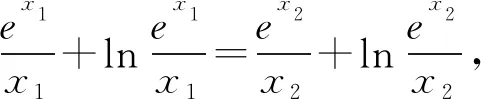


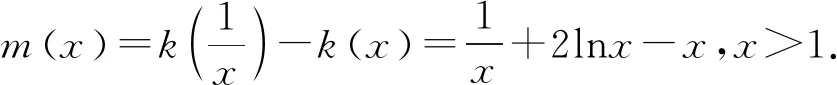

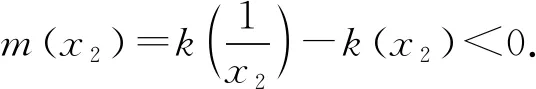
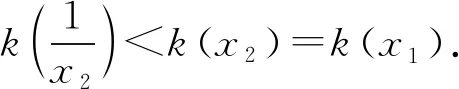
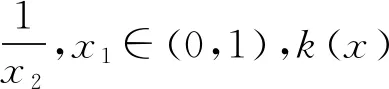
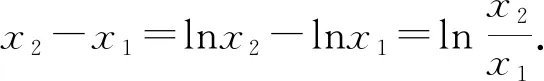
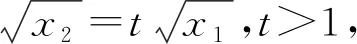
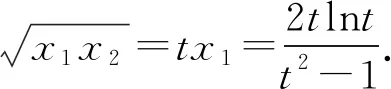
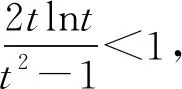
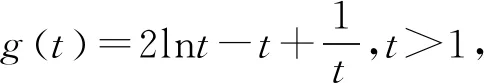
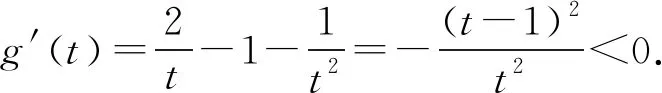
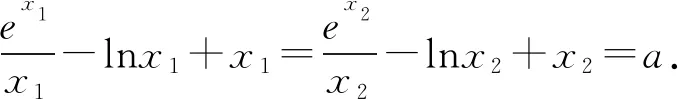
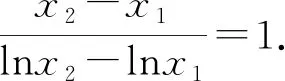
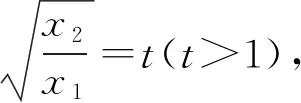

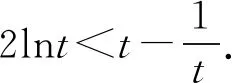
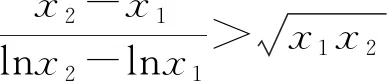
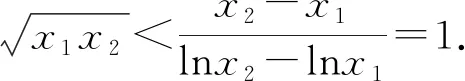

4 变式

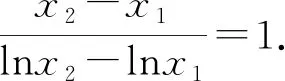
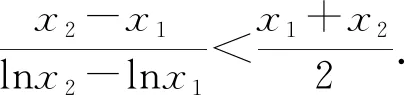



5 考题溯源