2022年新高考Ⅰ卷第21题的多解、推广与变式

刘才华

(山东省泰安市宁阳第一中学 271400)

1 试题呈现

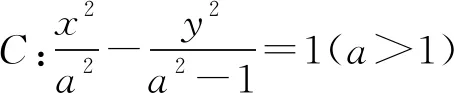
(1)求直线l的斜率；

这是2022年新高考数学Ⅰ卷第21题，试题简洁明快，入手容易，深入难，在重视对基础知识、基本方法以及基本思想考查的同时，对学生的直观想象、数学运算等学科素养均有较高的要求.首先我们给出试题的两种解法，然后给出在双曲线、椭圆、圆和抛物线中的推广与变式，得到四个相关的命题.

2 试题解析

整理，得a4-4a2+4=0.

解得a2=2.

(1)设直线AP的方程为y=k(x-2)+1交C于点P(x1，y1).

(1-2k2)x2+(8k2-4k)x-8k2+8k-4=0.

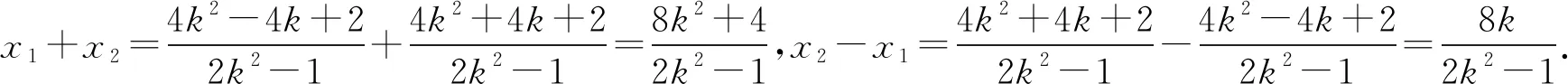
所以直线l的斜率为

故直线l的斜率为-1.

(1)由题意直线l的斜率存在，设直线l的方程为y=kx+t，P(x1，y1)，Q(x2，y2),

(1-2k2)x2-4ktx-2(t2+1)=0.

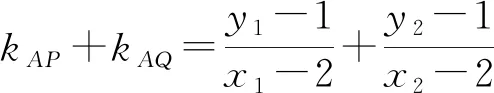
由kAP+kAQ=0，得k=-1.

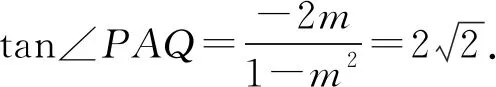
对试题第(1)问作进一步推广与变式，我们得到如下命题：

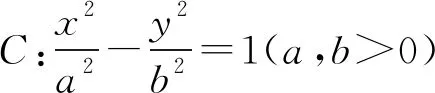
证明由题意直线l的斜率存在，设直线l的方程为y=kx+t，P(x1，y1)，Q(x2，y2),

(a2k2-b2)x2+2kta2x+a2t2+a2b2=0.

a2b2=b2m2-a2n2.

由点A(m，n)不在直线y=kx+t,得

mk+(t-n)≠0.

于是kAP+kAQ=0⟺2kx1x2+(t-n-mk)(x1+x2)+2mn-2mt=0

⟺mna2k2+(a2b2+nta2)k+(t-n)mb2=0

⟺mna2k2+(b2m2-a2n2+nta2)k+(t-n)mb2=0

⟺(na2k+mb2)[mk+(t-n)]=0

⟺na2k+mb2=0

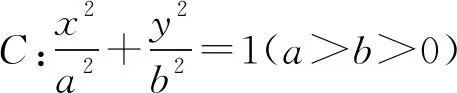
证明由题意直线l的斜率存在，设直线l的方程为y=kx+t，P(x1，y1)，Q(x2，y2),

(a2k2+b2)x2+2kta2x+a2t2-a2b2=0.

则Δ>0，且

a2b2=b2m2+a2n2.

由点A(m，n)不在直线y=kx+t上，得

mk+(t-n)≠0.

于是kAP+kAQ=0⟺2kx1x2+(t-n-mk)(x1+x2)+2mn-2mt=0

⟺mna2k2+(nta2-a2b2)k+(n-t)mb2=0

⟺mna2k2+(nta2-b2m2-a2n2)k+(n-t)mb2=0

⟺(na2k-mb2)[mk+(t-n)]=0

⟺na2k-mb2=0

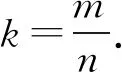
证明由题意直线l的斜率存在，设直线l的方程为y=kx+t，P(x1，y1)，Q(x2，y2),

(k2+1)x2+2ktx+t2-r2=0.

由点A(m，n)不在直线y=kx+t上，得

mk+(t-n)≠0.

于是kAP+kAQ=0⟺2kx1x2+(t-n-mk)(x1+x2)+2mn-2mt=0

⟺mnk2+(nt-r2)k+(n-t)m=0

⟺mnk2+(nt-m2-n2)k+(n-t)m=0

⟺(nk-m)[mk+(t-n)]=0

⟺nk-m=0

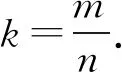
证明由题意直线l的斜率存在，设直线l的方程为y=kx+t，P(x1，y1)，Q(x2，y2),

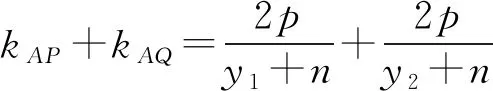
于是kAP+kAQ=0⟺y1+y2+2n=0