从一道联考题谈不等式恒成立问题的解题策略
2022-08-30俞国梁
俞国梁
(浙江省永康市永康外国语学校 321300)
纵观近些年的高考和各级各类模拟考,不等式恒成立求参数范围问题越来越受命题者的青睐,已成为常考常新的问题,因此该类问题是高考备考的一大重点.从内容来看,该类试题的交汇面广,综合考查函数、导数、不等式等方面的知识;从考查能力角度来看,该类试题不仅可以很好地考查考生的“四基”(基础知识、基本技能、基本思想、基本活动经验),还能考查考生的关键能力和数学核心素养(数学抽象、逻辑推理、数学建模、数据分析、直观想象、数学运算),是展示考生能力的一个很好的平台.但是从实际的教师教学和学生掌握情况来看,该类问题又是复习备考的一大难点.如何有效突破这一重点、难点,成为广大一线教师在复习备考中亟待解决的一大课题,现笔者结合自身教学实践与研究,以2021年山西省三重教育11月高三大联考导数题为例,阐述如何突破该类问题的解题策略.
1 问题呈现与分析
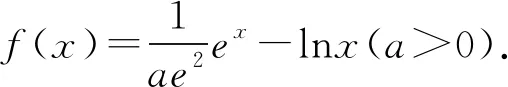
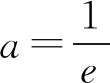
(2)若对∀x>0,f(x)≥lna+2恒成立,求实数a的取值范围.
分析该题是2021年山西省三重教育11月大联考理科第20题,第(1)问属于常规问题,本文不再赘述,重点论述第(2)问,此问是含有参数的不等式恒成立问题,本小题综合性强、解法灵活、难度较大,主要考查了利用导数研究函数的单调性,含参不等式恒成立求参数范围等知识,考查了学生分析问题、解决问题的能力及转化与化归等数学思想,体现了逻辑推理、数学运算等数学核心素养.本文尝试对本题的第(2)问从不同的角度予以思考,给出不同的解法.
2 解法探究
2.1 转化为函数最值法
对于一些含参不等式恒成立问题,将不等式朝着有利于通过导数判断单调性的方向变形,将不等式整理为一侧为常数(一般为零)的形式,根据题目的量词(∀或∃),将问题转化为函数最值与常数(一般为零)的不等关系,这是处理不等式问题最基本的通法之一.
解法1由f(x)≥lna+2,得
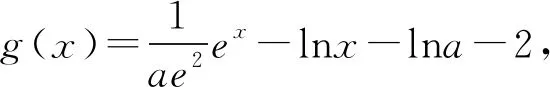
问题转化为g(x)min≥0,
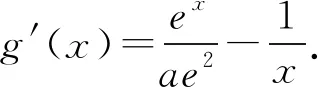
易知g′(x)在(0,+∞)上单调递增.
设x1
则g′(x1)<0,g′(x2)>0.
所以存在x0∈(x1,x2)使g′(x0)=0.
当0
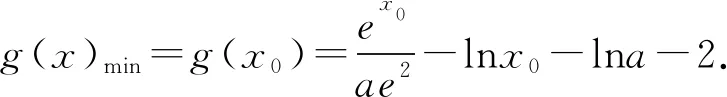
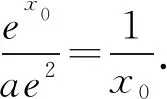
即lna=x0+lnx0-2.
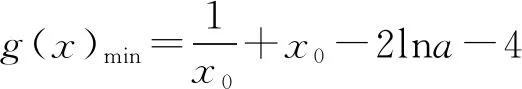
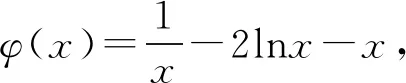
易知φ(x)在(0,+∞)上单调递减.
又φ(1)=0,则0 所以lna=x0+lnx0-2≤-1. 一些含参不等式中,将指数函数、对数函数综合考查,尤其是与ex,lnx有关的超越函数问题,若直接求导找零点(多数情况下是隐零点),往往复杂繁琐,此时若能巧妙运用一些“切线不等式”进行放缩,将复杂的超越函数转化为简单函数(以直代曲),常常可以起到化繁为简的效果.牢记两个重要的“切线不等式”:①ex≥x+1(x∈R,当且仅当x=0时等号成立);②lnx≤x-1(x∈R,当且仅当x=1时等号成立),这两个不等式是“切线放缩”法的基础. 解法2(利用ex≥ex放缩)由ex≥ex,得 当0 所以h(x)min=h(ae)=-2lna-2. 当x=1且x=ae时,f(x)-lna-2取最小值为-2lna-2. 故-2lna-2≥0. 当0 所以h(x)min=h(ln(ae2))=-2lna-2. 当x=1且x=ln(ae2)时,f(x)-lna-2取最小值为-2lna-2. 故-2lna-2≥0. 即ex-lna-2+x-lna-2≥x+lnx=elnx+lnx. 设φ(t)=et+t,则φ(x-lna-2)≥φ(lnx). 易知φ(t)为单调递增函数. 所以x-lna-2≥lnx. 即lna≤x-lnx-2. ex-lna-2-lna-2≥lnx. 即ex-lna-2+x-lna-2 =ex-lna-2+lnex-lna-2 ≥x+lnx. 设φ(t)=t+lnt, 则φ(ex-lna-2)≥φ(x). 易知φ(t)为单调递增函数. 所以ex-lna-2≥x. 又ex-1≥x(当且仅当x=1时等号成立), 解法6(同构函数“xex”法)由f(x)≥lna+2,整理,得xex≥ae2x·ln(ae2x). 即xex≥ln(ae2x)·eln(ae2x). 设φ(t)=tet(t>0),则 φ(x)≥φ[ln(ae2x)]. 求导,得φ′(t)=(t+1)et>0. 则φ(t)为单调递增函数. 所以x≥ln(ae2x). 即ex≥ae2x. 又ex-1≥x(当且仅当x=1时等号成立), 对一类函数不等式恒成立问题,可以通过取函数定义域中某个数,缩小参数的讨论范围,获得初步的参数范围,之后在此范围内继续讨论进而解决问题.在这个定义中,“取函数定义域中某一个数”,便相当于寻找一个能使题意成立的必要条件,而题目本身要寻求的参数的取值范围(或最值),相当于是使题意成立的充分必要条件.因此,在找到必要条件的基础上,只需要证明这个条件反过来能推出题意,即证明这个条件也是满足题意的充分条件.这样,充分性和必要性都成立,那么所求出的范围必然是题目所寻求的参数的准确取值范围,这便是必要性“探路”法. 解法7由f(x)≥lna+2,得 问题转化为g(x)≥0恒成立,则 则m(a)≥ex-1-lnx-1. 又ex-1≥x且x-1≥lnx(当且仅当x=1时两等号成立),则ex-1-lnx-1≥0. 所以g(x)=m(a)≥0. 有些不等式,将其适当变形,使之满足两个条件:(1)不等式变形后,不等号两侧的对应函数呈现凹凸反转的特点;(2)两侧对应函数在同一点取最值.如不等式F(x)≥0变形为f(x)≥g(x),f(x)为凹函数且在x=x0处取得最小值,g(x)为凸函数且在x=x0处取得最大值,问题转化为f(x0)≥g(x0). 解法8由f(x)≥lna+2,整理,得 则当0 所以m(x)min=m(1)=e. 若函数m(x)与函数n(x)互为反函数,则两函数图象关于直线y=x对称,于是我们不难明白不等式m(x)≥n(x)等价于m(x)≥x(或x≥n(x)).我们又知道同底的对数函数与指数函数互为反函数,所以在解决一些同时含有指数和对数的不等式问题时,若我们能将不等式变形为m(x)≥n(x)的形式,则可以借助m(x)≥x(或x≥n(x))解题,减少运算,化繁为简. 解法9由f(x)≥lna+2,整理,得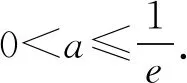
2.2“切线”放缩法
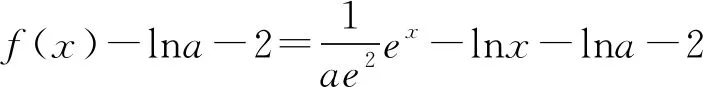
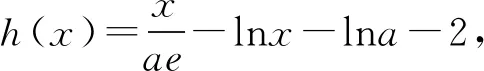
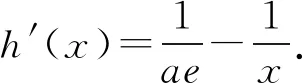
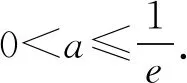
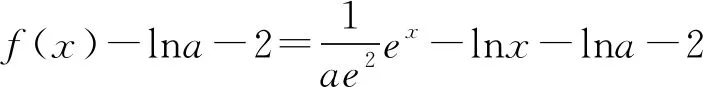
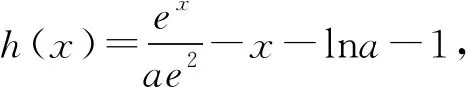
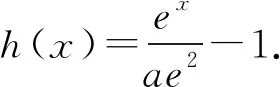
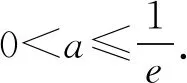
2.3 “同构”法
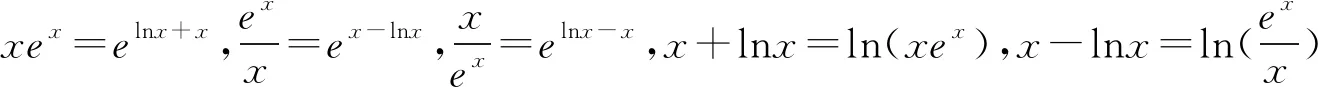
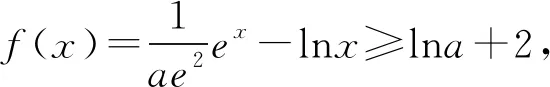
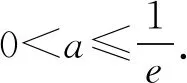
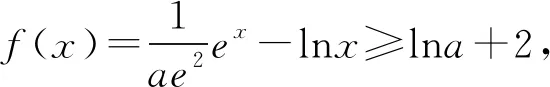
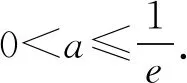
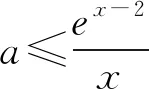
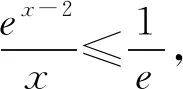
2.4 必要性“探路”法
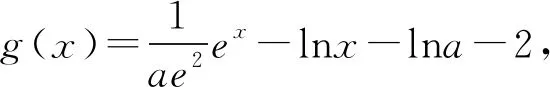
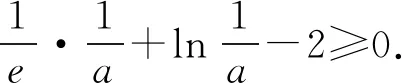
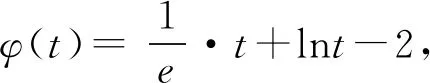
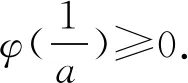
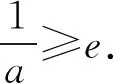
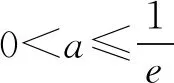
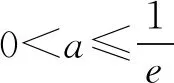
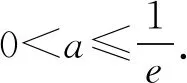
2.5 “凹凸”反转法
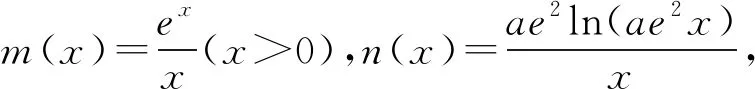
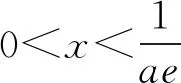
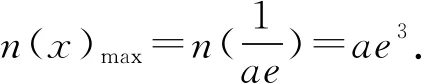
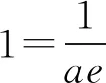
2.6 反函数法