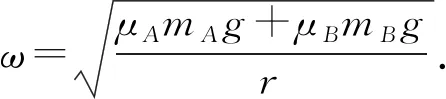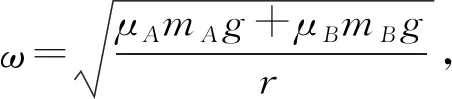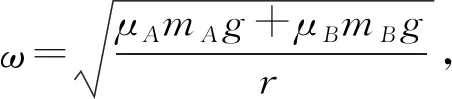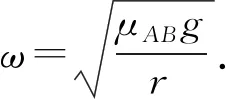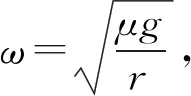探讨有约束条件下水平盘上物体做圆周运动的临界条件

邓柳咏 李广凌

(广东省广州市南武中学 510220)

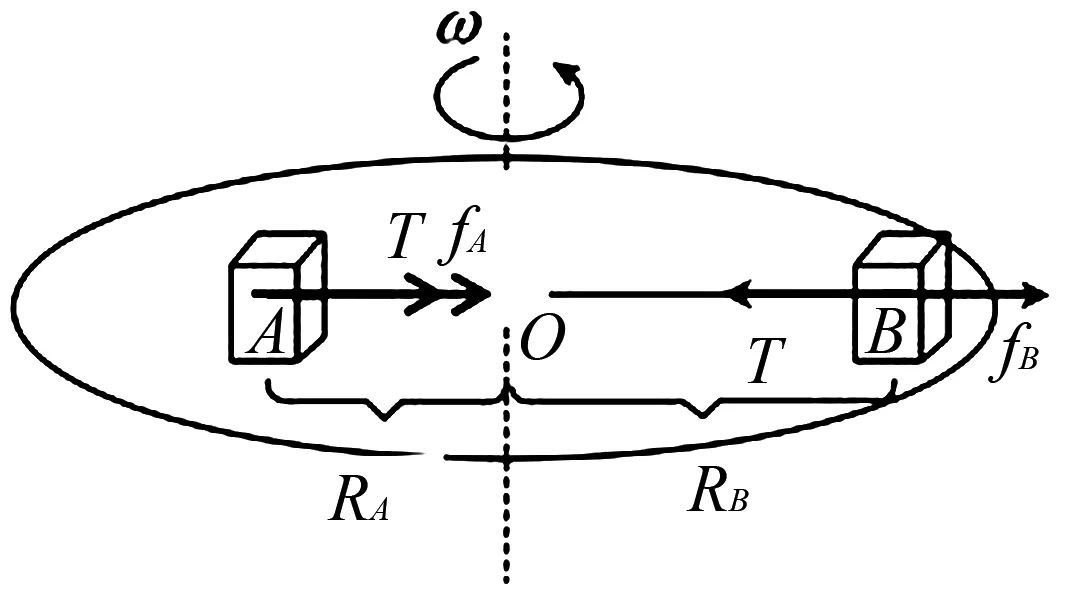
题目如图1所示，在匀速转动的水平盘上，沿半径方向放着用细线相连的质量分别为mA和mB的物体A和B；它们分居圆心两侧，与圆心距离分别为RA和RB，且RA

图1

该题目主要是考查有约束条件下匀速转动水平盘的临界状态的分析，解题的关键是判断发生滑动时作离心运动时的状态，究竟是物体A离心运动，从而拉动物体B，还是物体B离心运动，从而拉动物体A.

思路分析假设两物体刚好发生滑动时，A作离心运动，B作近心运动，列出各自的牛顿第二定律方程，联立解出对应的角速度，并讨论对应的运动状态是否存在.

分析过程假设两物体刚好发生滑动时，由于绳子的作用，A作离心运动，B作近心运动，A和B受到圆盘的摩擦力为滑动摩擦力,分别表示为fA=μAmAg和fB=μBmBg.对A和B受力分析，如图2所示，应用牛顿第二定律：

图2

T+μAmAg=mAω2RA

①

T-μBmBg=mBω2RB

②

联立①式和②式可得到系统的临界角速度关系式为：

μAmAg+μBmBg=(mARA-mBRB)ω2

讨论：

(1)mARA-mBRB>0，则假设是成立的，得到临界角速度大小表达式为：

③

(2)mARA-mBRB<0，则假设是不成立的，则运动状态只能为A作近心运动，B作离心运动，根据其对应的受力分析，列出牛顿第二定律方程，如下：

T-μAmAg=mAω2RA

④

T+μBmBg=mBω2RB

⑤

联立④式和⑤式，可得到：

⑥

讨论对比③式和⑥式，可以得出下列可以直接应用的结论：

(1)系统刚好发生滑动时，物体的运动状态由mARA-mBRB的数值决定.若mARA>mBRB，则物体A离心运动，从而拉动物体B；若mARA

应用如图3所示，匀速转动的水平圆盘上放有质量分别为2 kg和3 kg的小物体A、B，A、B间用细线沿半径方向相连.它们到转轴的距离分别为rA=0.2m、rB=0.3 m.A、B与盘面间的最大静摩擦力均为重力的0.4倍.g取10 m/s2，现极其缓慢地增大圆盘的角速度，当两物体刚好发生滑动时，圆盘的角速度约为____.

图3

深入探讨回归问题可以知道，上文得到的临界角速度的表达式属于我们常说的“二级结论”.在应用时，“二级结论”有特定的情景要求，使得其适用性受限.为了解决适用性受限的问题，现在利用上文的提到的分析方法来分析水平盘上作圆周运动的其他种情况来来深入探讨一般的分析方法.

如图4所示，粗糙水平圆盘上，可视为质点的木块A、B叠放在一起，放在水平转台上随转台一起绕固定转轴匀速转动，A的质量为mA，B的质量为mB.已知A、B到转动轴的距离为r，A与B间的动摩擦因数为μAB，B与转台间的动摩擦因数为μ，(最大静摩擦力等于滑动摩擦力，重力加速度为g).现缓慢地增大圆盘的角速度，请分析需要什么条件才能使A与B保持相对静止.

图4

结合情景观察，可能出现两种不同的运动情景：

(1)物体A和B同时向外作离心运动.

(2)物体A作离心运动，物体B还可以跟随圆盘作圆周运动.

分析方法隔离分析物体A和B的受力情况，假设可能存在情景(2)，列出各自的牛顿第二定律方程组，并结合情景所隐含的数量条件，解出特定的数量关系，并讨论对应运动状态是否存在.解答过程如下：

分别对物体A和B的受力分析，应用牛顿第二定律：

fAB=mAω2r

⑦

f-fAB=mBω2r

⑧