研磨习题载体 变式引领复习
2022-08-30徐凯钰王桢宇
徐凯钰 王桢宇
(1.北京航空航天大学工科实验班冯如书院217414班 100083;2.北京市第一七一中学 100011)
1 题目呈现与解析
例题(2022年朝阳区高三第一学期期末试卷20题第(3)问)设g(x)=aex-x2,当a∈(1,e)时,求函数g(x)的零点个数,并说明理由.
本题可以求导判断g(x)的单调性,进而通过零点存在定理判断零点个数,参考答案通过等价变换,转化为第(2)问的结论,不再赘述,但测试反馈发现,同学们大多没有注意到两问之间的联系,而是直接求导,致使运算难度增大,鉴于其更具有通法意义,本文采用该方法.
解析因为g′(x)=aex-2x,g″(x)=aex-2,
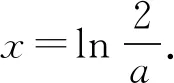



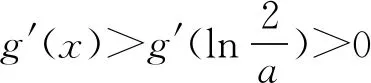
所以g(x) 在(-∞,+∞)单调递增.
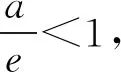
故存在唯一零点x1∈(-1,0)使得g(x1)=0.
题目不难,解法也众多,不再赘述,试题解罢,笔者思考一个问题,为什么原题给出了a∈(1,e)这个条件,若扩大这个范围会对函数零点的求解带来什么样的影响呢?命题人在此为了回避哪些难点呢?为了寻找答案,故做如下探索.
2 试题变式
2.1 变式改编,找点升级
变式1设g(x)=aex-x2,当a∈(1,+∞)时,求函数g(x)的零点个数.
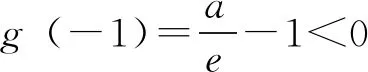
2.1.1 特殊值代入找点
由于需要在(-∞,0)找某点x1满足g(x1)<0,所以我尝试了令x1= -a.
因为g(-a)=a(e-a-a),又a>1,
所以e-a<1,所以e-a-a<0.
即g(-a)<0.
所以∃x1=-a∈(-∞,0)满足g(x1)<0.
2.1.2 指对互换找点


2.1.3 利用不等式进行放缩
考虑到x→-∞时,ex→0,所以寻找h(x)使得x→-∞时,h(x)→0,且同时满足h(x)>ex.
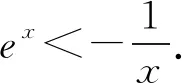

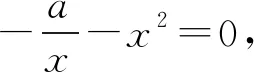
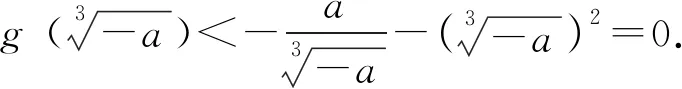
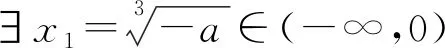
2.1.4 利用取值范围进行放缩
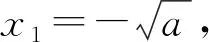
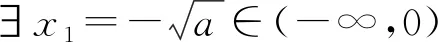
2.2 逐段筛选,隐形零点
变式2设g(x)=aex-x2,当a∈R时,求函数g(x)的零点个数.

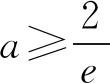

所以当x∈(-∞,x1), (x2,+∞),g′(x)>0,g(x)单调递增;当x∈(x1,x2),g′(x)<0,g(x)单调递减.

所以g(x)在(-∞,0)内有1个零点.
下面讨论g(x)在(0,+∞)的零点个数.
g′(1)=ae-2<0,所以x1∈(0,1),x2>1.
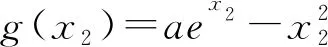



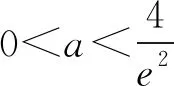

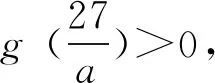
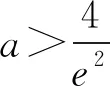
2.3 极值点偏移
变式3设g(x)=aex-x2,当g(x)在(0,+∞)有两个零点时,求证:两个零点和大于4.
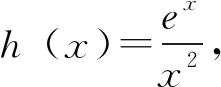

所以当x∈(0,2),h′(x)< 0,h(x)单调递减;
当x∈(2,+∞),h′(x)>0,h(x)单调递增.
已知h(x1)=h(x2),故x2>2>x1>0.
若证x1+x2>4,即证2>x1>4-x2>0.
注意到x1和4-x2都处于(0,2)减区间内,
只需证h(x1)
构造新函数t(x)=h(x) -h(4-x),x∈(2,4),即证t(x)<0在x∈(2,4)恒成立,显然t(2)=0,若能证明x∈(2,4)时t′(x)<0,则此题得证.



教师点评“极值点偏移”问题近年来在高考题、模拟题中频繁出现,2016年全国Ⅰ卷和2021年新课标Ⅰ卷都是以其作为压轴题考查.这类问题包含了转化与化归、函数与方程等数学思想,常见解法是基于对称变换的思想,构造新函数讨论单调性求解.特别的,上文有这样一句话“t(2)=0,若能证明x∈(2,4)时t′(x)<0,则此题得证.”这个思维方式是不严谨的,因为此时t′(x)<0是t(x)<0的充分非必要条件,答题过程应该逆序书写,即求出t′(x)<0,说明函数单调递减,进而结合端点值说明t(x)<0.
