谙命题之道 明解题之本
2022-08-30林春明张如椿
林春明 张如椿
(福建省福清第二中学 350300)
1 试题呈现
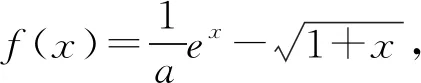

本题是2021-2022学年佛山第一次质量检测第22题的第(2)问,试题设问清新自然又颇具特色,立意朴实又不失新颖.以含参不等式的证明进行呈现,乍看平淡无奇,细细品味后却感觉内涵丰富.本题在考查基础知识的同时,注重考查能力,将知识、能力与素质的考查融为一体,突出考查数学理性思维,着重考查对数学本质的理解,真正全面考查数学素养.
2 解题策略剖析
命题组采用分类讨论来求解.








即证(2-a2)t2-2at+a2≥0.
由基本不等式,得




由上述过程,通过适当的推演,不难管窥命题者的命题手法.
3 命制思路揣析
通过以上的解题策略剖析过程,我们不难得知命题者命制这一试题的思路历程.
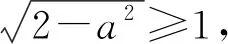
所谓命题如制谜,解题如猜谜,至此,我们不难揣析到:命题者将一个常规的问题,通过逐步包装转换,将其变为一个新颖的试题.而作为解题者的我们,则需通过转换手段,将一个陌生的问题,不断地转换到我们熟悉的情境和问题,就可轻松将其解决.
4 命题手法综析
对上述命题手法作进一步的综合分析,我们可得到关于此类问题的一般化命制思路.
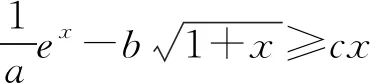



基于上述理论分析结果,通过分别具有梯形机构及回转支承的两台架车,对其在转向过程中的操作力大小进行对比试验验证,初始条件如下:
(7)进行合理设问.
由此步骤,可产生与此类似的一系列试题.
5 新题命制探析
基于上述试题命制手法,笔者尝试命制一些新题.

(5)利用基本不等式,

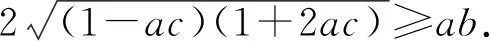



(7)构造函数f(x),进行合理设问.


(1)讨论f(x)的单调性;
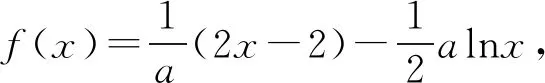
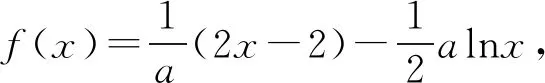
(1)讨论f(x)的单调性;
随着构成不等式模型的基本素材的调整,参数取值的不同设定,函数f(x)形式的改变,问题设问的不同铺陈,根据上述命题思路,还可命制出各类相关试题,此处不再一一阐述.
数学解题有五重境界,从低阶到高阶分别是:“正确解题”“一题多解”“多题一解”“发现定理”“自己编题”.通过上述基于命题视角的试题研究,我们实现了解题策略分析、命题手法剖析、新题命制探析,对试题有了更深入的认识,在这个命题探究过程中,提升了自己的解题境界.
