近场水下爆炸瞬态强非线性流固耦合无网格数值模拟研究1)

王平平 张阿漫, 彭玉祥 孟子飞

* (哈尔滨工程大学船舶工程学院,哈尔滨 150001)

† (中山大学海洋工程与技术学院,广东珠海 519000)

引言

近场水下爆炸主要包括冲击波、气泡脉动和射流以及结构毁伤等.当炸药在水中发生爆炸,对周围水介质产生剧烈的挤压作用,造成水介质的密度、压力以及速度急剧上升,在水中产生强间断冲击波.炸药引爆后形成的气态爆轰产物被水包围形成气泡,在内部高压和外部流场压力作用下发生膨胀和收缩,此过程被称为气泡脉动.气泡脉动频率与船体结构的固有频率往往非常接近,因此容易引起船舶结构发生共振,对其总纵强度非常不利,甚至导致舰船折断.气泡在自由液面以及舰船结构表面等边界耦合作用下还会形成高速气泡射流,其速度可达数十米甚至上百米每秒,使舰船结构产生严重破坏.目前,水下武器的引爆多采用非触发引信的形式,在舰船附近发生爆炸,因此研究近场水下爆炸问题对保护舰船生命力具有重要意义.

目前水下爆炸数值模拟大多基于商业软件或自编程序的有网格方法,对于解决水下爆炸中的复杂多相界面捕捉和结构大变形问题常常面临较大困难.因此,许多学者将目光转向了新兴的无网格算法,其中以光滑粒子流体动力学(smoothed particle hydrodynamics,SPH) 方法最为成熟和常用.由于SPH 方法在求解强非线性大变形和动边界问题时避免了网格畸变,省去了界面捕捉等复杂过程,因此在处理移动界面和大变形问题上具有先天优势.下面将从冲击波、气泡以及结构毁伤三个方面对当前的SPH 研究现状进行介绍.

针对水下爆炸冲击波研究,2002 年Liu 等[1]首次将传统人工黏性SPH 方法应用到水下爆炸问题的仿真中,模拟了二维有限方形域中水下爆炸冲击波的传播和反射等现象,较好地捕捉了冲击波的幅值和位置.同样基于传统人工黏性SPH 方法,杨刚等[2]模拟了二维近自由面水下爆炸和炸药爆轰过程,并研究了空气对压力场和密度场的影响.采用传统人工黏性SPH 方法,明付仁[3]模拟了三维近自由面水下爆炸,考察了自由面下不同反射区冲击波的波形,并探究了不同爆深时近自由面冲击载荷特性.但需要指出的是,传统人工黏性SPH 方法在处理流场间断时常常导致剧烈的非物理振荡或引起过大的数值耗散.为了更好地处理流场的间断,获得更加精确的数值结果,一些学者[4-7]将黎曼思想引入SPH中得到黎曼SPH 方法,并将其应用到水下爆炸模拟中.例如,蔡志文[8]采用一阶黎曼SPH 方法模拟了二维水下爆炸问题,并探究了不同的近似黎曼求解器对压力场的影响.可以看出,已有的水下爆炸冲击波SPH 模拟多局限在二维框架下,且大多数研究采用了传统的人工黏性力来实现对冲击波的捕捉,但人工黏性力的大小常需要通过人工参数调节,过大的人工黏性将会导致冲击波峰值的降低,而过小的黏性力会引起剧烈的数值振荡.虽然有少数研究采用了黎曼SPH 算法,但由于未采用重构算法往往导致间断附近出现较大的数值耗散和非物理振荡.上述原因导致已有的SPH 方法得到的水下爆炸冲击波往往无法达到令人满意的精度.

对于水下爆炸气泡动力学的研究,尽管网格方法取得了很大成功[9],但其在处理复杂界面时仍然存在较大挑战,需要精细的网格分辨率和高精度的计算格式.考虑到SPH 方法在处理多相界面、流体大变形等问题上具有显著优势,近年来一些学者将SPH 方法应用到水下爆炸气泡数值模拟中.然而,由于水下爆炸气泡的模拟往往涉及到强可压缩、大密度比、粒子体积变化过大以及计算效率低等问题,因此相关的SPH 研究非常有限.Liu 等[10]采用传统人工黏性SPH 方法模拟了二维水下爆炸气泡在密闭室内的运动,并研究了此过程中冲击波的传播以及气泡尺寸和形状的演化.Pineda 等[11]基于黎曼SPH 模拟了自由场和刚性壁面附近的二维气泡坍塌,并分析了包括压力波和射流等现象的主要特征,但所采用的黎曼SPH 数值耗散较大,且未对气泡膨胀和收缩过程中粒子体积变化过大的问题做出处理.为了解决粒子体积变化过大导致的精度下降问题,Sun 等[12-13]在传统人工黏性SPH 的框架下提出了粒子体积自适应方案,该方案通过对粒子进行分割和合并以降低粒子的体积变化,模拟了自由表面和刚性壁面附近气泡的动力学特性.同样为了解决粒子体积变化过大的问题,Peng 等[14]基于一阶黎曼SPH 方法提出了粒子再生技术,并模拟了刚性壁面附近和自由面附近的二维气泡坍塌.总的来看,目前基于无网格SPH 方法的水下爆炸气泡研究大多局限于二维情况,且多数采用了传统的人工黏性SPH 多相流模型.该模型对于水气界面的密度间断处理常带来压力不稳定等问题.为了使水气界面稳定,一些研究对于气相采用远大于物理声速的人工声速,导致无法考虑真实的气体可压性,且稳定时间步非常小,大大降低了计算效率.

对于近场水下爆炸的结构毁伤模拟,近年来无网格SPH 方法也得到了初步应用.张阿漫等[15]采用基于体积近似的SPH 方法在二维框架下模拟了水下接触爆炸对单层和双层钢板的毁伤.文献[3,15-16]采用SPH-SPS 耦合算法模拟了水下接触爆炸对简单平板的毁伤,并探究了不同起爆方式对结构毁伤程度的影响.此外还采用SPH-FEM 耦合算法模拟了接触爆炸对板架结构的毁伤.彭玉祥[17]采用SPH算法模拟了近场水下爆炸对圆板、双层壳结构以及舷侧结构的破坏.上述SPH 水下爆炸结构毁伤模拟虽然取得了一些成果,但需要指出的是由于计算效率和精度的限制,这些研究主要考虑了水下爆炸前期冲击波对结构的破坏,而忽略了水下爆炸气泡与结构的相互作用,因此对水下爆炸结构毁伤的研究并不完整.而且,这些研究的冲击波载荷均基于传统的人工黏性SPH 方法求解得到,导致载荷误差较大.

针对上述近场水下爆炸SPH 模拟存在的不足,本文推导了适用于间断流场的多相流黎曼SPH 数值模型,开发基于RKPM 的结构损伤断裂求解器,并应用法向通量边界条件构建SPH-RKPM 流固耦合数值模型,实现对近场水下爆炸冲击波、气泡以及结构毁伤的高精度数值求解,并给出了水下爆炸载荷及其对结构的毁伤特性,以期为近场水下爆炸载荷预报提供理论和基础性技术支撑,为毁伤威力评估和舰船防护结构设计提供参考.

1 基本理论

1.1 黎曼SPH 间断流场模型

在SPH 方法[18]中,对于无黏流体,其拉格朗日形式的控制方程如下

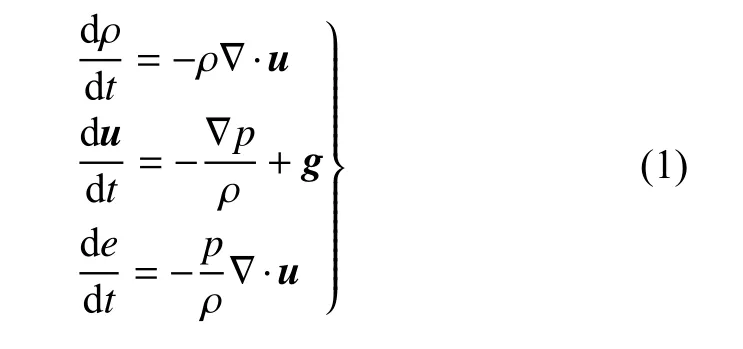
其中,e,p,g,u,ρ分别代表流体单位质量的内能、压力、重力加速度、速度和密度.通过核近似和粒子近似,可得到SPH 的离散控制方程如下

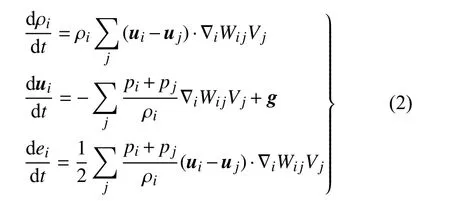
式中,Wij=W(|xi-xj|,hi) 为SPH 使用的核函数,常需要满足归一性、紧支性以及狄拉克性质,核函数的有效范围称为支持域,支持域的半径为kh,其中k是一个与所取核函数有关的常量,h称为光滑长度.本文中,如不特别说明均采用Wendland 核函数[19],且光滑长度取为2 倍粒子间距,即h=2Δx.下标i和j分别代表目标粒子和其支持域内的粒子.可以看出,核函数值的大小与粒子之间的距离以及光滑长度有关.

为了使控制方程(1)封闭,一般采用状态方程来表述流体的压力和密度、内能之间的关系.例如本文2.3 节、3.2 节和3.3 节中认为水是正压流体[20],采用如下Tait 状态方程

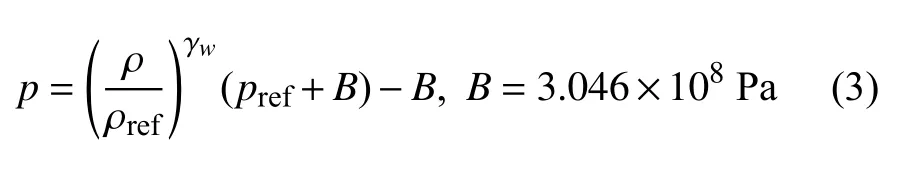
其中,绝热系数 γw=7.15,参考密度 ρref=998.0 kg/m3.考虑大气压力时参考压力pref=101325 Pa,否则pref=0.0 Pa.在3.1 节、3.4 节和3.5 节中需要考虑水内能变化对其压力的影响,即水为斜压流体,采用Mie-Gruneisen 状态方程,其具体形式和参数参考文献[10].

对于气体,在3.2 和3.3 节中认为其是正压[21],采用Cole 状态方程

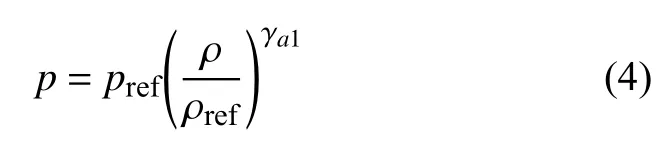
其中,绝热系数 γa1=1.25,pref=101325 Pa,ρref=2.0 kg/m3.在2.1 节中认为其是斜压气体,采用理想气体状态方程[22],如下

其中绝热系数 γa2取为1.4.此外,对于3.1 节、3.4 节和3.5 节中TNT 药包爆轰产生的气体,通过JWL 状态方程描述其压力和密度、比内能之间的关系,详见文献[10].

在传统的SPH 方法中,为了提供维持数值稳定的耗散,常常在动量与能量方程中加入人工黏性力项,但需要指出的是,这种方法对于流场间断的处理常常面临较大困难.具体来说,在间断附近,人工黏性力常常导致剧烈的非物理振荡,而在远离间断处,可能引起过大的数值耗散.为了解决这一问题,一些学者将黎曼思想引入SPH 中得到黎曼SPH 方法,该方法认为每两个相互作用的粒子对构成一维黎曼问题,且粒子对的连线中点存在间断,通过求解一维黎曼问题得到粒子之间的相互作用,进而得到整个计算域的解[23].基于上述思想,控制方程(2)变为如下形式

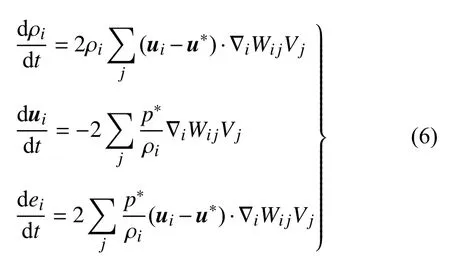
式中,p*和u*分别为中间变量,由黎曼求解器得到.本文中采用了适用于大密度比多相流的PVRS 近似黎曼求解器[24],如下

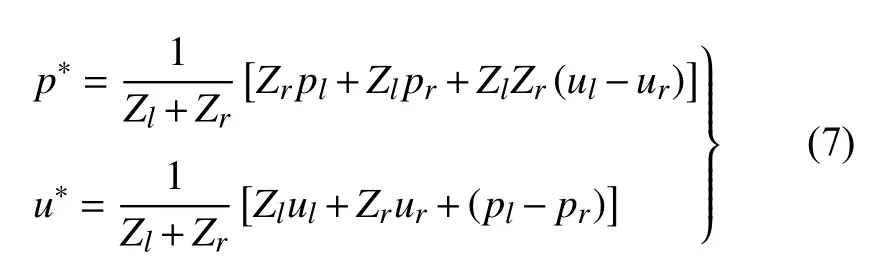
式中,下标l和r分别表示黎曼问题的左右状态,c表示流体的声速,Z为流体的阻抗,计算为Z=ρc.标量u*和中间变量u*的关系为

其中,eij=(xj-xi)/|xj-xi| 表 示由粒子i指向j的单位矢量.

不同于传统人工黏性力SPH 方法,黎曼SPH 通过黎曼求解器的固有数值黏性而非显式人工黏性来保证数值格式的稳定性,因此避免了相关的可调人工参数.更重要的是,由于采用黎曼求解器来确定粒子间的相互作用,黎曼SPH 更擅长处理间断问题,因此对于大密度比强间断多相流的模拟具有更高的精度.但同时,原始的黎曼SPH 方法直接将相互作用的粒子的物理量作为黎曼问题的初始左右状态,因此仅具有一阶精度,常常引起过大的数值耗散,导致精度下降.为解决这一问题,一些学者提出了适用于SPH 方法的黎曼高阶重构算法,例如MUSCL 重构[24-25]、WENO 重构[26-28]以及TENO[22]重构.对于本文中模拟的水下爆炸问题,选取了MUSCL 重构算法[25],该算法采用线性重构得到黎曼问题左右初始状态,对于变量 φ 的重构如下

其中,Δ φi和 Δ φj由下式求得

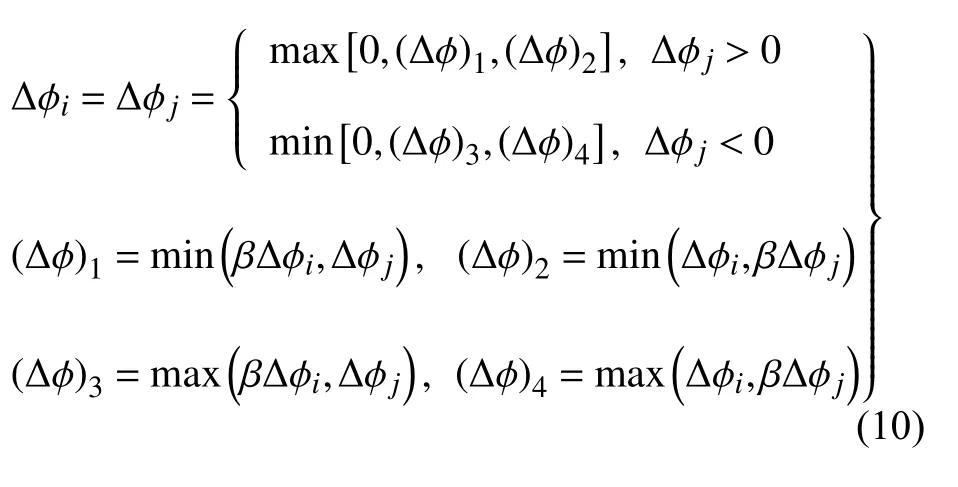
式中,常数 β 本文中取为1.5,变量 φ 的变化量 Δ φi和Δφj由下式计算得到

其中,矢量rji计算为rji=xj-xi.

1.2 RKPM 结构损伤断裂模型

上节中介绍了基于SPH 方法的流体计算模型,对于结构损伤断裂模型,也可以采用SPH 方法来建立.但由于SPH 方法中采用的是强形式的控制方程,导致自由边界无法自动满足,对于存在大量自由边界的复杂结构模拟存在较大困难,同时也不利于处理结构裂纹拓展中动态增加的内部自由边界.因此本文中采用基于弱形式控制方程的重构核粒子法(reproducing kernel particle method,RKPM)来模拟结构的弹塑性以及损伤断裂,目前RKPM 已经被广泛应用到舰船结构的爆炸毁伤响应预报当中[29-30].本文采用RKPM 壳单元来对结构进行建模,采用退化实体几何表述,仅需在壳中面布置一层粒子来对结构进行离散,依据虚功率原理,得到壳体的控制方程如下

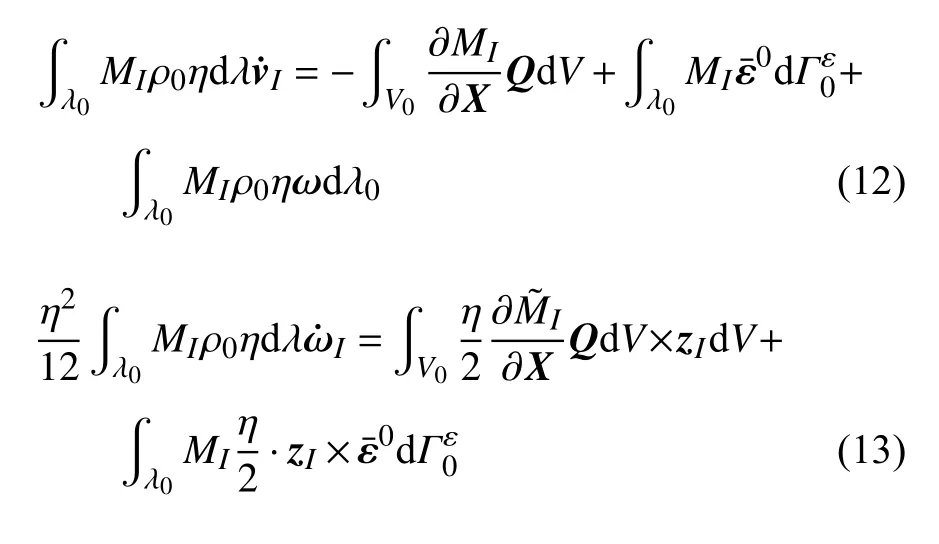
式中,ρ0为材料的初始密度,η 表示壳体的厚度,和分别为I粒子的速度和转动角速度的时间导数.MI和Q分别是RKPM 型函数和第一P-K (Piola-Kirchhoff)应力张量,和 ω 分别为结构牵引力以及单位质量体积力.表示型函数MI与壳厚度方向的参数坐标 ψ 的乘积,即=ψMI.zI表示I粒子的纤维矢量,V0为I粒子支持域的壳体,λ0为对应的壳体参考面,为牵引力边界.同时针对复杂结构的大变形损伤,需要结构的大变形接触检测以及接触力计算模型,参考文献[30],针对结构裂纹萌生及拓展,相关的材料弹塑性损伤本构模型,以及粒子的裂纹萌生拓展算法,可以参考文献[31].

1.3 流固耦合算法

在流固耦合界面上,需要满足动力连续和运动连续条件,也就是说界面上压力以及沿界面法向的速度要连续.为了满足上述条件,本文将结构粒子作为流体粒子的移动边界,并依据Leffe 等[32]提出的法向通量边界条件,来计算结构对流体的作用.此时,考虑结构作用的流体控制方程变为

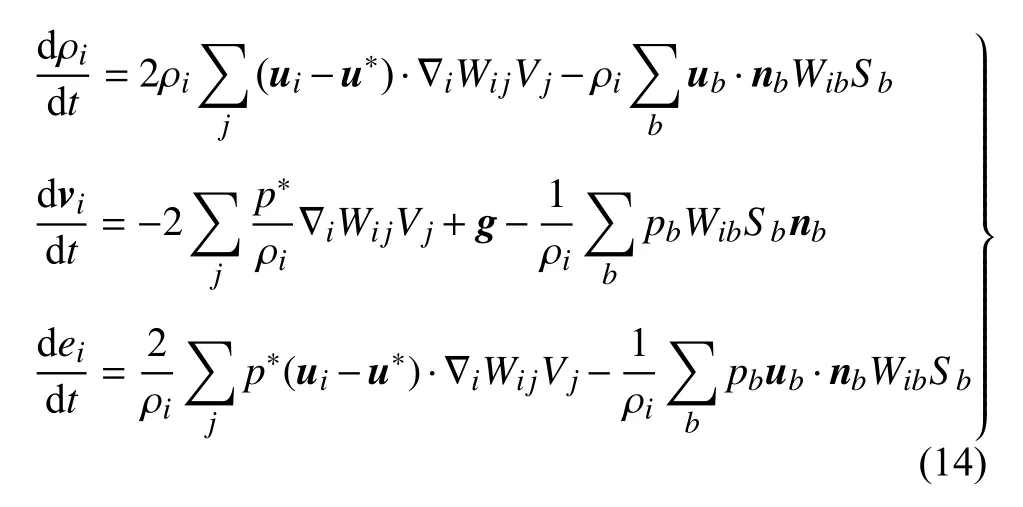
其中,下标b代表流体粒子i邻域内的结构粒子,nb和Sb分别为结构粒子的单位法向矢量和面积.

另一方面,对于结构粒子,通过对周围流体粒子压力的SPH 插值得到其受到的流体载荷pfb,具体插值计算公式如下[30]

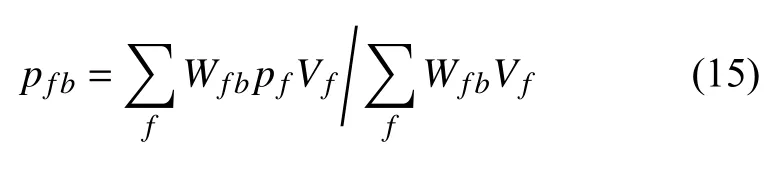
上述算法可以很好地实现流体粒子与单层壳结构粒子的流固耦合,从而建立起SPH-RKPM 流固耦合算法,对于处理水下爆炸瞬态流固耦合问题具有良好的精度[32-33].

2 数值验证

为验证所建立的流场和结构数值模型以及流固耦合算法的数值精度,本节分别模拟了激波管、平板大变形撕裂和水射流冲击弹性板三个算例,并将得到的结果与解析解或其他数值解进行对比.

2.1 激波管

首先,为了验证所建立的黎曼SPH 方法对激波的捕捉精度,本文首先求解了经典的一维“激波-密度波相互作用问题”[34-35].此算例的初始条件为

可以发现,此算例中初始时刻压力、密度和速度在x=1处均呈间断分布,这将导致密度场中产生马赫数为3 的激波和正弦波,因此可以被用来检验数值模型捕捉间断的能力.

为验证当前SPH 方法的收敛性和精度,采用0.05,0.025 和0.0125 三种粒子分辨率对计算域进行离散,得到的黎曼SPH 结果如图1 所示,可以看到无论是密度还是速度分布曲线,随着粒子分辨率的提升,SPH 的结果与文献[36]中的经典五阶WENO方法得到的参考解的差别减小.当粒子分辨率为0.0125时,SPH 结果与参考解高度吻合,从而证明了当前提出的黎曼SPH 方法对于此类可压缩间断流动问题,具有良好的精度和收敛性,为后续模拟水下爆炸问题奠定了基础.

图1 黎曼SPH 方法得到的“激波-密度波相互作用问题”在t=1.8时刻的密度和速度分布Fig.1 Density and velocity distributions of the shock-density wave interaction at t=1.8 obtained by the present Riemann SPH scheme

2.2 圆管受压屈曲

针对RKPM 结构计算模型,采用一个外压作用下的圆柱管的非线性动力屈曲算例来进行验证.在图2 中给出了结构的几何参数、边界条件设置以及相应的材料参数.计算中对于材料的弹塑性响应采用各向同性线性硬化假设,将粒子间距设置为0.02 m,共采用5940 个粒子对圆管进行几何离散.

图2 圆管受压动力屈曲计算模型Fig.2 Computational model of the dynamic buckling of the circular tube under compression

文献[37]中Kyriakide 的实验结果给出了圆管会在第三种屈曲模式中被压溃.通过屈曲分析得到的解析解表明圆管在该模式下压溃所需要的外界压力为30.43 MPa,在实验中测得的临界压力为28.26 MPa.采用RKPM 计算得到的该模式下屈曲所需的外界压力载荷为29.64 MPa.

在计算中,圆管中间部分的加载压力在1.0 ms内线性增加,然后维持在29.64 MPa,在1.5 ms 对圆柱壳的圆周方向坐标加入一个缩放扰动1+cos(3θ)/20,在第三种屈曲模式下对粒子坐标进行扰动.最终计算得到圆管的动力屈曲过程如图3 所示,从图中可以看到计算在2.0 ms 圆柱壳初步产生了第三种屈曲模式的应力分布,然后在2.2 ms 结构就发生了动力屈曲,到2.5 ms 圆管就被完全压溃,壳体压缩到发生接触,之后结构的变形变得稳定.

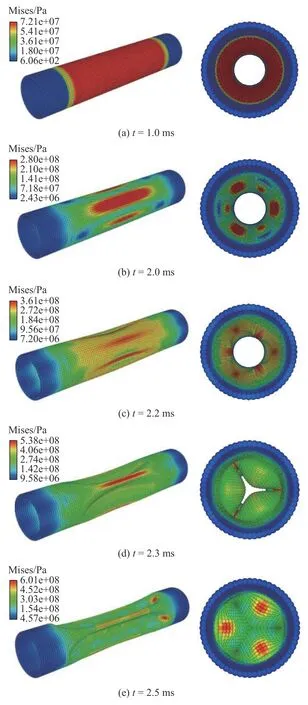
图3 圆管受压动力屈曲过程Fig.3 Dynamic buckling process of the circular tube under compression

在图4 中将RKPM 计算得到圆管最终屈曲变形构型与实验结果进行了对比,从图中可以看到数值计算得到屈曲模式与实验结果吻合良好,验证了RKPM 壳体大变形数值计算模型的有效性.实验中圆管一端结构出现了断裂,但数值模拟当中未考虑材料的损伤,因此壳体没有出现断裂.

图4 圆管屈曲变形数值结果(上)与文献[37]中的实验结果(下)对比Fig.4 Comparison of the buckling deformation of the circular tube between numerical results (upper) and the experimental results in Ref.[37] (lower)

2.3 水射流冲击弹性板

在本节中,通过模拟高速水射流冲击弹性平板算例,以验证当前采用的流固耦合算法在强冲击问题中的精度.其计算模型如图5 所示,一个半径为1.5 mm 的球头柱形水射流,其长度为12 mm,以570 m/s 的初始速度冲击一个四周刚固的方形板中心,方形板的长度和厚度分别是30 mm 和5.9 mm,其材料参数为:密度1170 kg/m3,弹性模量3.3 GPa,泊松比0.36.分别采用本文提出的SPHRKPM 方法和软件ABAQUS 中基于网格的耦合欧拉-拉格朗日(coupled Eulerian-Lagrangian,CEL)方法模拟此算例,其中粒子间距或网格大小均取为0.05 mm.

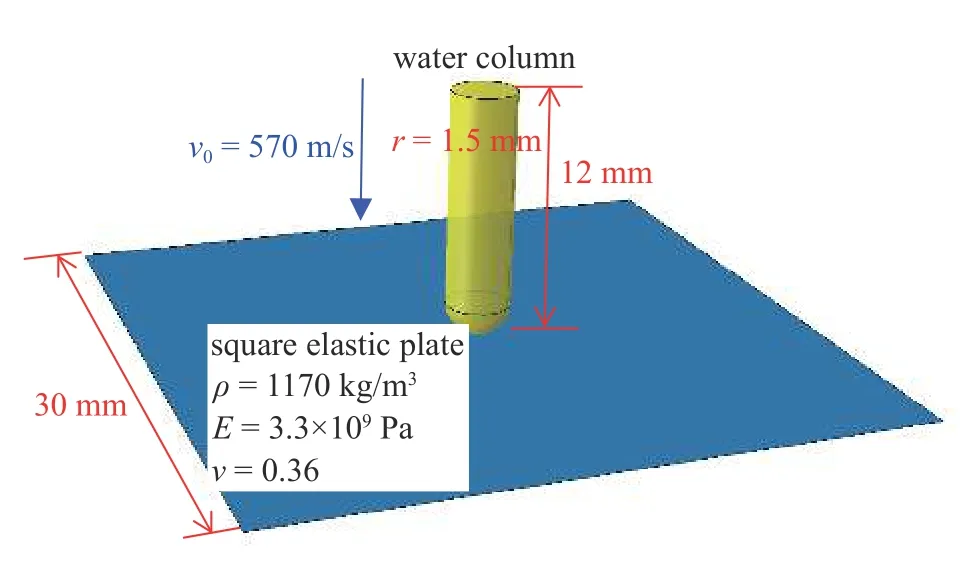
图5 水射流冲击弹性板计算模型Fig.5 Computational model of the water jet impacting elastic plate

图6 给出了CEL 和SPH-RKPM 得到的几个典型时刻的结果,可以发现,在撞击到方板后,水柱头部被压平,形成一个紧贴方板的圆形水面,随着其不断朝向板运动,水柱长度不断缩短,而圆形水面半径迅速增大.可以发现,CEL 方法只在模拟后期捕捉到少许飞溅的水滴,这是因为其采用了流体体积分数(volume of fluid,VOF)方法来重构界面,当网格分辨率不足时,较小的飞溅水滴难以精细捕捉,而SPH方法由于其天然的拉格朗日特性,采用自由运动的粒子来代表流体,能更好地捕捉流体飞溅,此算例很好地体现了SPH 方法在模拟流体飞溅现象上的优势.

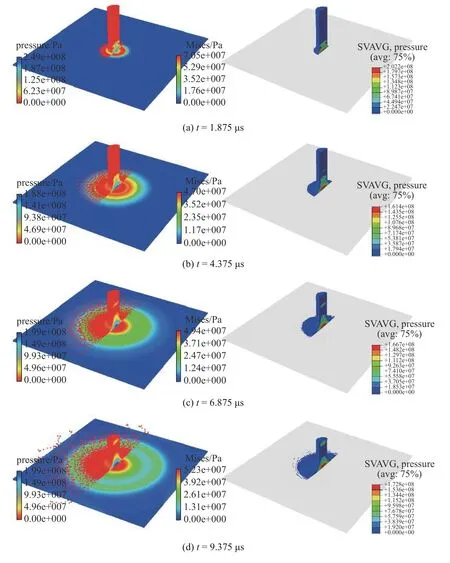
图6 几个典型时刻SPH-RKPM(左)和CEL(右)结果对比Fig.6 Comparison of SPH-RKPM (left) and CEL (right) results at several typical moments

为了定量地比较两种方法的结果,图7 给出了方板中心点位置处的流场压力以及板的位移时历曲线,并与文献[38]中的实验结果进行对比.可以发现,当射流冲击平板时,中心点的压力迅速增大,其幅值约为0.9 GPa,随后压力降低并逐渐稳定在约0.2 GPa.两种数值方法得到的压力峰值和变化趋势与实验结果均较为接近,但CEL 方法得到的压力曲线在后期出现较为明显的振荡,而由于当前的SPH 采用了黎曼方法,因此得到的压力变化更加平稳.由图7(b)可以看出,在冲击过程中中心点的位移不断增大,在 0～2 μs 和2～12 μs 呈分段线性变 化,2 μs 之前增速较大,而 2～12 μs 增速变缓.大体而言,两种方法得到的位移曲线较为吻合.通过图7 给出的流场压力和结构响应验证了当前采用的SPH-RKPM 流固耦合方法具有较高的精 度.

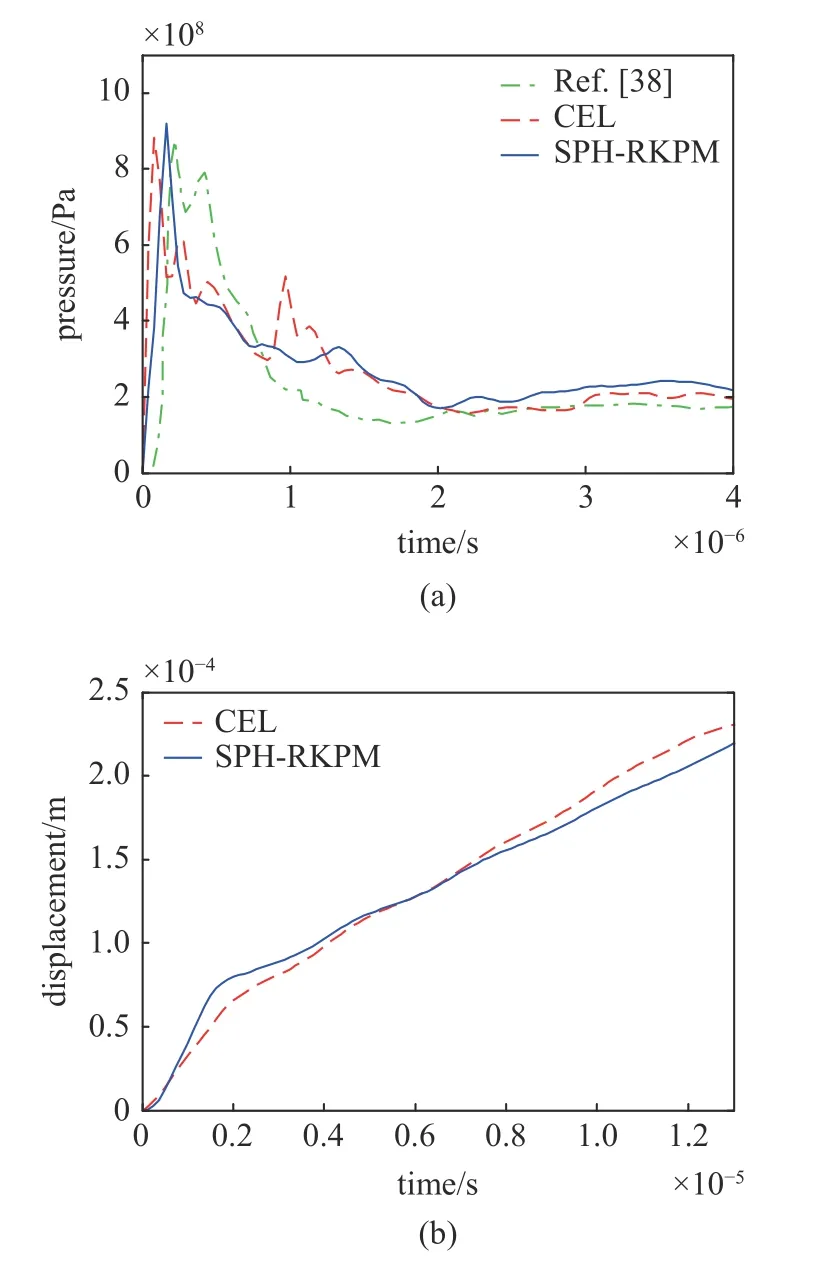
图7 不同方法得到的圆板中心点位置处的(a)流场压力和(b)结构位移时历曲线Fig.7 Time histories of (a) flow field pressure and (b) structural displacement at the central point of circular plate obtained by different methods

3 算例结果

3.1 水下爆炸冲击波模拟

首先,基于所建立的黎曼SPH 流体动力学模型,对三维水下爆炸冲击波传播过程进行模拟.计算模型为边长0.7 m 的方形水域,水域中心布置一个半径为0.05 m 的球形TNT 药包,爆点位于药包中心,在距药包中心0.3 m 和0.35 m 处分别布置有两个测点A和B来记录压力时历.整个计算域的粒子分辨率为6.25 mm.此算例中水采用Mie-Gruneisen 状态方程,TNT 药包采用JWL 状态方程[39].为了验证本文采用的黎曼SPH 方法在激波捕捉方面的优势,本节中分别采用传统的人工黏性SPH 方法和黎曼SPH 方法,得到的三个典型时刻的压力场分布如图8所示.可以发现TNT 药包起爆后,产生迅速向外传播的压力波.从压力场看,两种方法得到的结果存在以下几点区别:首先,传统人工黏性SPH 得到的压力场在水气界面存在压力不连续,且波阵面附近存在多个峰值,而黎曼SPH 方法得到的压力场较为光顺;其次,相比于传统人工黏性SPH 方法,黎曼SPH 得到的波阵面压力峰值略大,说明其数值耗散相对较小;最后,黎曼SPH 得到的波阵面更窄,具有更好的间断特性.

图8 分别采用人工黏性SPH 方法(左)和当前的黎曼SPH 方法(右)得到的三个典型时刻的流场压力分布Fig.8 Pressure distribution of the flow field at three typical time instants,obtained by using artificial viscous SPH method (left) and the present Riemann SPH method (right),respectively

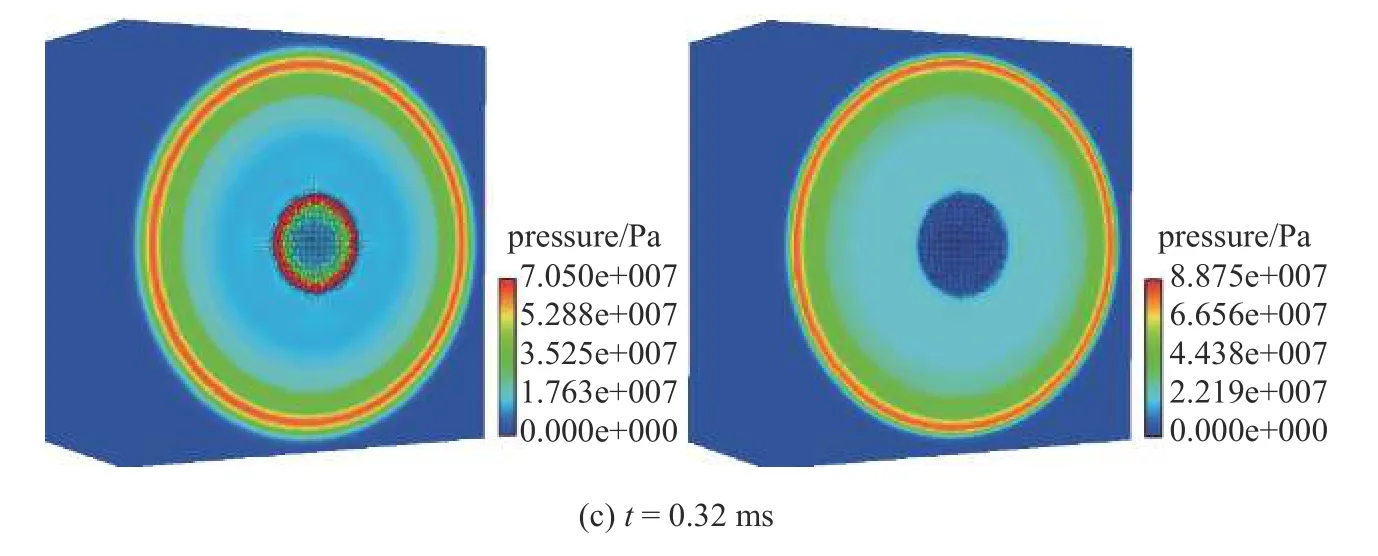
图8 分别采用人工黏性SPH 方法(左)和当前的黎曼SPH 方法(右)得到的三个典型时刻的流场压力分布(续)Fig.8 Pressure distribution of the flow field at three typical time instants,obtained by using artificial viscous SPH method (left) and the present Riemann SPH method (right),respectively (continued)

为了定量地比较两种方法,图9 给出了得到的两个测点的压力时历对比,并与Geers-Hunter 模型[40](简称GH 模型)得到的解进行对比.可以发现,两种SPH 方法得到的曲线在波阵面附近存在明显的压力爬升期,且在峰值后呈现不同程度的压力振荡.但相对而言,黎曼SPH 的爬升期更小,压力振荡更弱一些,更重要的是压力峰值精度明显提升,与GH 模型吻合良好.

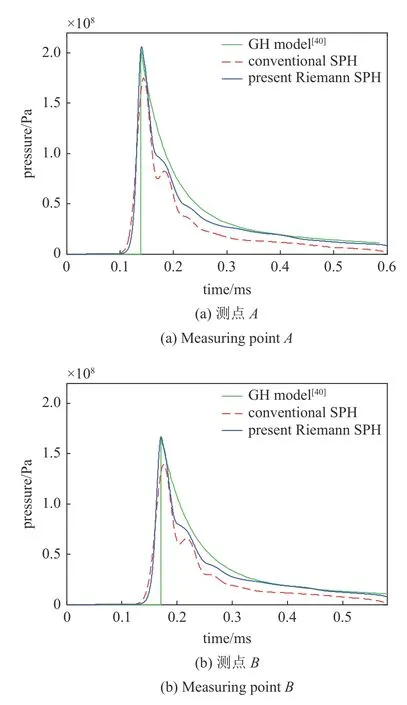
图9 不同方法得到的测点压力时历Fig.9 Pressure histories of measuring points obtained by different methods

3.2 水下爆炸气泡模拟

本节对自由场中的水下爆炸气泡进行模拟.该水下爆炸实验由哈尔滨工程大学在江西实验中心的小型爆炸水箱中完成.实验中1 g 的黑索金炸药在1.7 m 水深处引爆.由文献[20]可确定气泡相应的初始条件为r0=0.02 m,初始压力为122 MPa.对于水面上方的空气,其初始压力设置为101325 Pa.计算域的初始粒子间距取为r0/8.考虑到气泡脉动过程中气体粒子体积变化剧烈,导致与周围粒子水粒子的分辨率差异十分显著,引起SPH 数值精度大大降低,甚至会导致计算崩溃[41],因此,本文采用了Sun 等[13]提出的自适应粒子分割与合并算法,该算法以粒子的体积和粒子之间的距离作为判据,对满足预设条件的水粒子和气泡粒子进行自动的分割与合并,以确保粒子的体积变化在一个较小的范围内.此外,为了维持整个系统的守恒性,依据质量、动量和能量守恒,得到粒子分割前后的物理量之间的关系.通过上述处理,有效地克服了传统SPH方法在模拟高压气泡时存在的精度低、稳定性差的难题.

图10 显示了实验和SPH 得到的几个典型时刻的压力场.可以看出,在内外压差的作用下,气泡迅速发生膨胀.在膨胀初期,向外辐射冲击波.在第一个膨胀过程中气泡呈球形,但在气泡收缩过程中,由于重力的作用,气泡下方压力要大于上方压力,导致气泡下半部分的收缩速度要大于上半部分,因此气泡上浮,同时产生向上的气泡射流.此过程中气泡不再呈圆形.在35.5 ms 左右,射流穿透气泡上表面形成环状气泡,此时气泡体积最小.由于高速射流的穿透,气泡在垂向上被拉长,在回弹过程中呈梨形,如图10(f)所示.由图10 可以看出,SPH 获得的气泡运动过程与实验结果基本吻合,进一步验证了模型的有效性和精度.

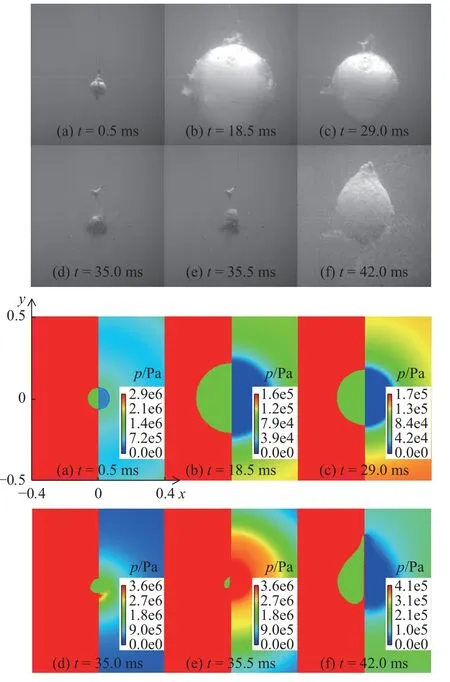
图10 水下爆炸实验与SPH 数值结果对比Fig.10 Comparison between underwater explosion experiment and SPH numerical results

图11 给出了SPH 得到的气泡的等效半径时历曲线,其中等效半径req由下式计算得到

图11 水下爆炸气泡等效半径时历Fig.11 Time history of equivalent radius of the underwater explosion bubble

式中Vb代表气泡粒子的体积.可以看出,气泡半径经历了先增大再减小然后再变大的历程.在第一个脉动过程中,气泡最大等效半径和脉动周期分别为0.204 m 和35.34 ms.将SPH 得到的曲线与实验结果以及Keller 模型解[42]进行对比可以发现,与实验数据相比,SPH 结果得到的气泡最大等效半径略小,但周期吻合非常好.SPH 的结果与Keller 模型解相比,气泡最大等效半径几乎完全相同,但气泡脉动周期略微偏大.

3.3 水下爆炸气泡与圆板的相互作用

在近场水下爆炸过程中,结构不仅会受到冲击波载荷的作用,同时气泡的脉动和射流也会造成结构的变形和毁伤.目前已有的水下爆炸SPH 模拟中仅考虑前期冲击波载荷的作用,而由于计算精度和效率的限制,对于后期的气泡脉动和射流对结构的作用未见相关研究.基于本文建立的SPH-RKPM 流固耦合方法,本节进一步模拟了水下爆炸高压气泡对背空平板的作用.

该算例的计算模型如下:一个初始半径为0.025 m 的球形气泡位于水深0.3 m 处,其初始压力为95 MPa.在水面上有一个半径为0.5 m 的圆板,其上方为空气,圆板的厚度取为0.01 m,四周刚性固定.重力大小为g=9.8 m/s2,方向竖直向下.圆板采用Q235 钢材,密度 为 ρ0=7850 kg/m3,杨氏模量E=211 GPa,泊松比 ν=0.3,采用的是Johnson-Cook 强化弹塑性模型,具体参数见文献[43].计算域的粒子分辨率取为5 mm.

模拟得到的几个典型时刻的流场粒子分布与压力分布如图12 所示,相应时刻的板的Mises 应力和等效塑性应变分布如图13 所示.由于气泡初始压力远大于周围的水,气泡迅速膨胀并向外辐射强烈的冲击波,冲击波向四周传播,到达平板后发生反射.冲击波的作用使圆板出现了明显的应力,如图13(a)所示.可以发现,当冲击波反射过后,气泡膨胀仍然对周围的水有挤压作用,导致平板与气泡中间形成一个高压力区,如图12(b)所示,在此高压区的作用下,平板的Mises 应力不断增大,在2 ms 左右其幅值达到约256 MPa,板的中心位置发生了塑性变形.随着气泡的膨胀,泡内压力迅速降低,小于周围水的压力.由于运动惯性,气泡仍继续膨胀,但速度明显降低,因此周围水受到的扰动变小,压力也变小,因而板的Mises 应力值减小,但等效塑性应变分布保持不变.在约15 ms 时,气泡体积达到最大值,此时气泡的膨胀速度为0,在周围流场挤压下开始发生收缩.由于气泡下方水的压力大于气泡上方,因此气泡下方的坍塌速度也要高于上方,生成向上的高速射流.在约45.5 ms 时,射流穿透气泡上表面,形成中空的环形气泡,如图12(e)所示.当气泡射流到达板下方时,会导致圆板中心区域产生较大的流场载荷,约为8 MPa,如图12(f)所示.在气泡射流的冲击下,圆板中心的Mises 应力显著增大,最大约为261 MPa,同时等效塑性应变也略有增大,如图13(f)所示.

图12 几个典型时刻的流场压力(左)和粒子分布(右)Fig.12 Flow field pressure (left) and particle distributions (right) at several typical time instants

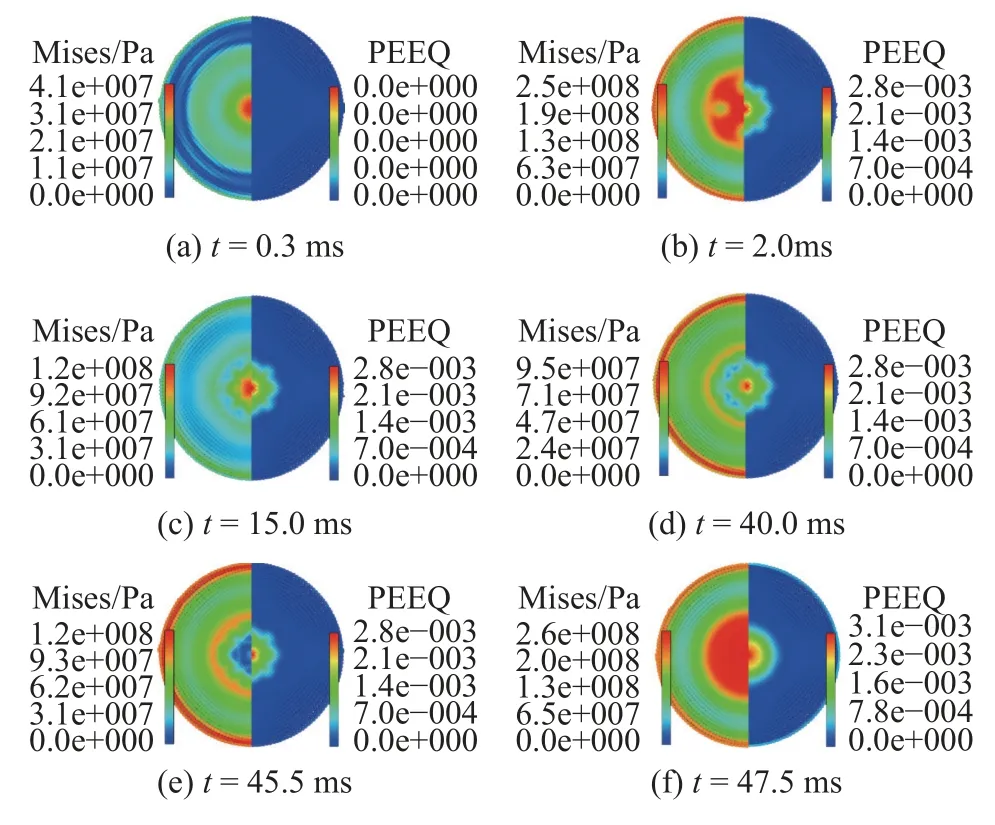
图13 几个典型时刻圆板的Mises 应力和等效塑性应变分布Fig.13 Mises stress and equivalent plastic strain distributions of the circular plate at several typical time instants

图14 定量给出了该算例中平板中心点的Mises应力以及位移的时历曲线.可以看到,与图13 一致,在模拟初期冲击波作用下圆板中心点应力迅速增大,峰值约为253 MPa,且随着应力波的反射,中心点应力出现较为剧烈的振荡.在气泡膨胀过程中,中心点应力在100 MPa 呈缓慢下降趋势,在气泡收缩的后期(43～46 ms),圆板中心点的应力迅速降低.随着气泡射流的产生,中心点的应力峰值再次迅速增大,其峰值约为261 MPa.由位移时历曲线可以发现,整个模拟过程中位移主要有两个峰值,其大小分别约为0.01165 m 和0.0169 m.第一个峰值的产生与前期的冲击波载荷有关,而第二个峰值由气泡射流载荷引起.可以发现,气泡射流导致的结构应力和变形均大于前期冲击波.

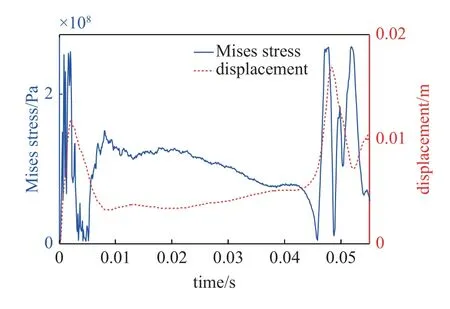
图14 圆板中心点的Mises 应力和位移时历曲线Fig.14 Time histories of the Mises stress and displacement of the center point of the circular plate

3.4 水下爆炸对舷侧结构的毁伤模拟

在上一节采用SPH-RKPM 流固耦合模型对爆炸气泡与简单平板的耦合进行了模拟,本节对接触爆炸作用下的舰船舷侧结构的毁伤进行研究.计算模型的设置如图15 所示,整个结构的壳体结构厚度设置为8 mm,材料采用945 钢,材料的初始屈服应力设置为 σy0=440 MPa.本文采用了线性硬化模型,硬化模量Ep设置为1000 MPa.对于本文中的水下爆炸毁伤算例,材料的应变率效应不能忽略,其采用Cowper-Symonds 模型[30,45]描述,此时动态屈服应力σyd计算为

图15 舰船舷侧防护结构受接触爆炸作用示意图,灰色粒子为装药Fig.15 Schematic diagram of the ship side protective structure subjected to contact explosion,with grey particles as charge

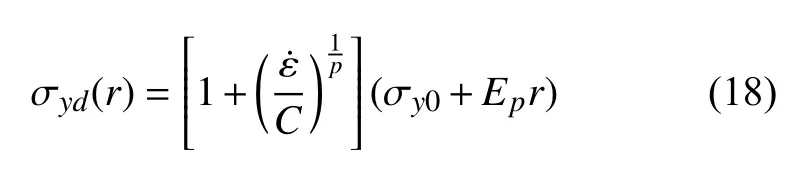
式中,r代表各向同性强化的状态变量,是塑性应变率.材料常数设为C=9870,p=2.43.材料损伤演化由Lemaitre 损伤模型[44]得到,损伤判据参数设为Dc=0.32,临界损伤应变=0.16,断裂应变=0.28.计算中采用均匀的粒子分布,粒子间距设置为0.02 m,TNT 当量为10 kg,流体和结构的时间步长均设置为1.0 × 10-6s.

图16 给出了0.25 ms 时的水中压力云图、爆炸气体产物的形态以及结构的变形,在结构的变形构型上绘制出了壳结构厚度方向最外层积分点上的Mises 等效应力云图.从图中可以看出,在计算开始之后,随着爆炸产物的膨胀,与装药接触的船体板立刻产生了局部的凹陷大变形,并在炸药接触的中心部分结构发生了破裂,同时加强筋和面板的交叉部位产生了应力集中现象.

图16 水下接触爆炸作用下舰船舷侧防护结构在 t=0.25 ms 时的流场压力云图以及结构的Mises 应力云图Fig.16 Pressure fields of the flow field and Mises stress fields of the warship side protective structure under underwater contact explosion att=0.25 ms

图17 给出了几个典型时刻,水下接触爆炸作用下舰船舷侧防护结构的变形构型以及应力云图,在每个时刻的应力云图的右侧都单独显示了弧形吸能板的变形.从图中可以看出,t=0.5 ms 时在爆炸作用下与装药紧挨着的面板发生了局部凹陷和局部断裂,同时应力波传播到了内层舱壁上,之后在t=1.0 ms 时结构变形加剧,并且外层舱壁产生的断裂破片碰撞到了内部的舱壁上,内部弧形吸能板产生了初步的变形,之后防护结构进一步变形,最外侧两层防护舱壁均产生了较大的断裂破口,并与内部舱壁发生了接触碰撞,到t=4.0 ms 时结构的断裂破口趋于稳定,最靠近爆点的弧形吸能板被完全压溃,产生了动力屈曲.

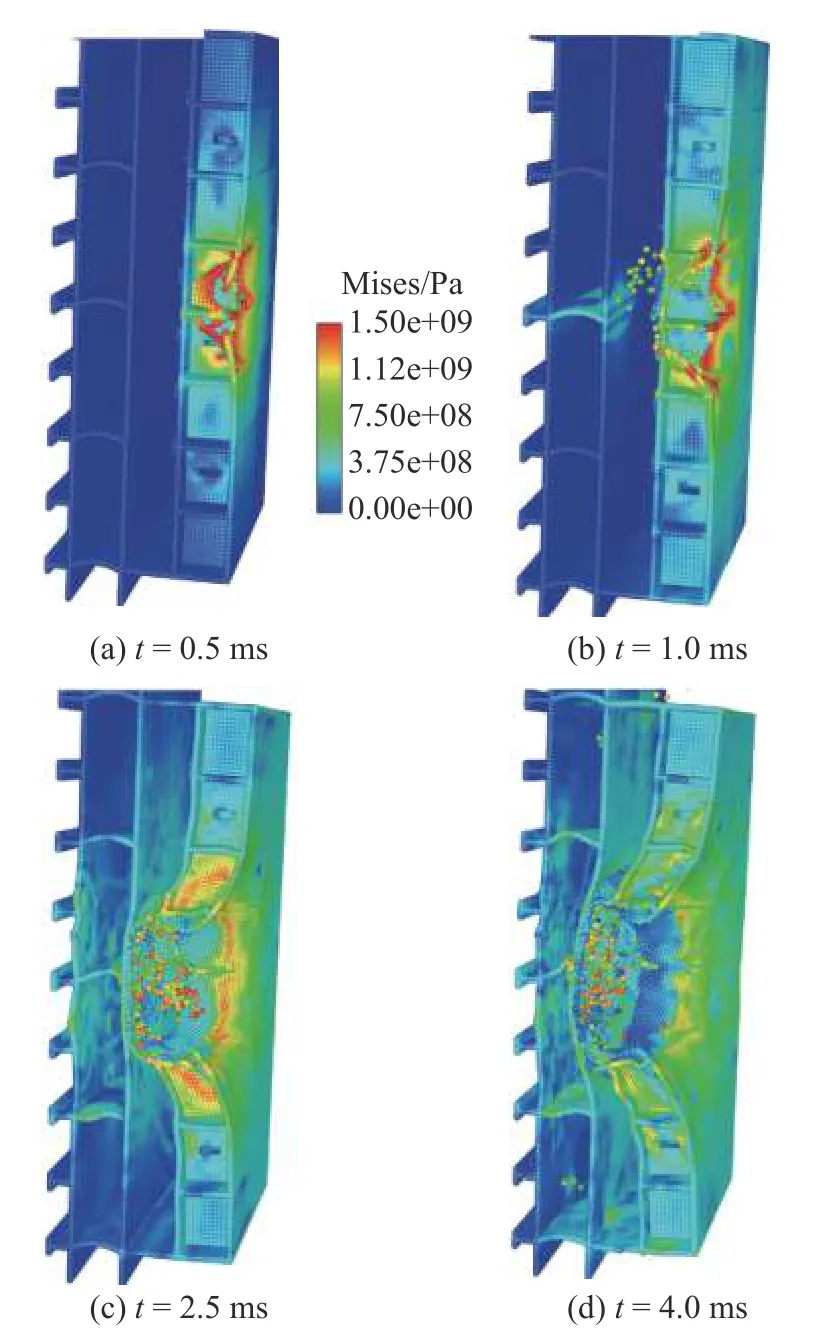
图17 水下接触爆炸载荷作用下双层底几个典型时刻的Mises 应力云图Fig.17 Mises stress fields at several typical time instants of the double bottom under underwater contact explosion loading

3.5 水下爆炸对潜艇结构的毁伤模拟

最后,基于本文建立的SPH-RKPM 流固耦合模型,模拟了近场水下爆炸对潜艇结构的毁伤.计算模型纵剖面如图18 所示,潜艇长度为110.5 m,耐压壳半径为5.6 m.在潜艇中部附近下方水域中有一个半径为0.65 m 的球形TNT 药包,药包中心距离潜艇外壳1.0 m.潜艇所用材料及参数与上节相同.整个模型采用均匀的粒子分布,粒子间距设置为0.2 m,流体和结构的时间步长均设置为2.0 × 10-7s.

图18 水下爆炸对潜艇结构的毁伤计算模型Fig.18 Computational model of submarine structure damaged by underwater explosion

图19 给出了几个典型时刻的流场压力分布和结构的Mises 应力分布.可以发现炸药起爆后变为高温高压气体,在水中形成强烈冲击波,在冲击波和爆轰气体共同作用下,潜艇外板迅速产生变形屈服并形成局部凹陷和破口.随着爆轰气体的膨胀和冲击波的传播,破口半径不断增大,屈服区域迅速向四周扩展,但由于径向上舱段间的环形肋板的存在,相邻舱段的应力和变形明显降低,减缓了破口的增大,说明其可以有效地增强潜艇的抗水下爆炸毁伤能力.

图19 水下爆炸对潜艇结构的毁伤SPH-RKPM 数值结果Fig.19 SPH-RKPM numerical results of submarine structure damage caused by underwater explosion

4 结论

本文针对近场水下爆炸流固耦合问题,在前期研究的基础上,利用无网格粒子法的天然拉格朗日优势,开发了适用于间断流场求解的黎曼SPH 方法和结构损伤断裂模拟的RKPM 方法,并应用法向通量边界建立了高精度SPH-RKPM 瞬态流固耦合模型.首先通过几个典型算例验证了上述算法的精度,在此基础上,对水下爆炸冲击波传播、气泡脉动和射流以及结构毁伤等现象进行了数值模拟,得到以下结论.

(1)相对于传统人工黏性SPH 方法,本文建立的二阶黎曼SPH 方法在模拟水下爆炸冲击波时,在多相界面处可以得到更加连续的压力场,以及更加尖锐的波阵面和更加准确的压力峰值;通过引入粒子自适应分割和合并算法,能有效地克服气泡脉动过程粒子体积变化导致的精度下降问题,从而实现水下爆炸气泡的动力学特性的高精度求解.

(2)基于RKPM 方法,采用退化实体几何表述,并应用Lemaitre 损伤模型,开发了基于粒子法的裂纹萌生拓展算法,可以较好地模拟壳结构的大变形动力屈曲以及损伤断裂行为.

(3)应用法向通量边界条件和SPH 插值,建立了SPH 流体和RKPM 单层壳结构的瞬态强非线性流固耦合模型,该模型对于高速水射流和水下爆炸等瞬态冲击问题具有良好的数值精度.

(4)依据SPH-RKPM 流固耦合模型模拟了水下爆炸气泡与圆板的相互作用,气泡在脉动后期产生了指向圆板的高速射流载荷,前期的冲击波载荷和后期的射流载荷均会对结构造成较大的冲击;此外模拟了水下接触爆炸对舰船舷侧防护结构以及潜艇结构的毁伤,给出了结构的变形和毁伤特性.

致谢

感谢哈尔滨工程大学博士研究生薛冰在论文撰写中提供的帮助.