基于相对增益矩阵的惯量响应空间耦合特征分析

2022-08-30朱林田政鳞王正宇武志刚龙霏易杨

电力建设 2022年9期

朱林，田政鳞，王正宇，武志刚，龙霏，易杨

(1.华南理工大学电力学院，广州市 510641；2.广东电网有限责任公司电力调度控制中心，广州市 510600)

0 引言

随着“双碳”目标的提出和落实，中国能源系统将持续加快清洁低碳转型发展，预计到2060年风电和光伏发电量占比将超过60%[1]。与此同时，为实现新能源的跨区域传输和消纳，多条大容量高压直流输电工程正陆续投入使用[2]。一方面，基于电力电子变流器的新能源和直流输电与系统频率进行解耦，遭受扰动时不能响应电网的频率变化；另一方面，新能源的出力波动和直流输电的闭锁故障容易引发大额功率冲击。特别是随着起惯性支撑作用的同步机组逐步被替代，传统电网将转变为高比例非同步电源的低惯量电力系统，频率调控面临着巨大压力。

惯量响应是系统遭受扰动后频率动态响应重要的初始阶段，低惯量系统在惯量响应阶段的频率变化率(rate of change of frequency，RoCoF)通常较高，导致频率在一次调频动作前下降速度过快，容易触发低频减载装置动作[3-5]。因此，国内外学者提出通过配置快速频率响应(fast frequency response，FFR)资源来改善在惯量响应阶段的系统频率特性[6-7]。

然而，当前针对惯量响应的研究多采用单机系统频率响应(system frequency response，SFR)模型[8-9]，由于忽略了网络拓扑结构并假设全网频率统一，未能体现出惯量响应的空间分布，在分析空间因素对系统惯量响应的影响时具有较大的局限性[10]。对此，国内外学者对频率动态响应的空间特征进行了广泛讨论。文献[11]通过RoCoF等指标构造了频率动态响应的时空分布特征描述矩阵，但尚未对空间分布特征与系统机电动态行为的耦合特征进行全面论证；文献[12-13]进一步探讨了网络拓扑结构、功率扰动位置和风电渗透率引起的惯量分布变化对局部惯量中心RoCoF的影响，但缺乏对空间影响因素的分析评价指标。目前，频率动态响应的空间特征还处于定性分析阶段，迫切需要在频率动态响应空间特征的定量化评估方面深入研究。以往，相对增益矩阵(relative gain array，RGA)常被用于量化分析不同FACTS装置控制器之间或控制器不同控制回路之间的交互影响[14-17]。近年来，亦有学者将相对增益矩阵应用于控制系统以外的电力系统空间耦合性分析中，如文献[18-20]基于系统无功功率与母线电压的传递函数，通过计算相对增益矩阵获得母线电压之间的耦合关系，在划分电压控制区域上取得了不错的效果，这也为分析电力系统惯量响应的空间耦合特性提供了借鉴。

有鉴于此，文章推导多机系统惯量响应模型，引入相对增益矩阵的理论方法，采用相对增益作为量化指标表征惯量响应与不同位置有功扰动之间的耦合程度，分析惯量响应的空间耦合特征。最后，以IEEE 39节点测试系统为例，验证所提方法的正确性和有效性。

1 考虑空间特征的惯量响应建模

1.1 惯量响应的空间差异性

目前，电力系统惯量响应主要采用时域仿真或基于SFR模型进行分析。时域仿真法通过求解系统的微分代数方程组模型，计算扰动后各状态量的数值解，具有较高的精度。BPA、PSS/E等电力系统专业仿真软件均能提供全状态时域仿真功能。

SFR模型忽略网络拓扑结构的影响，在全网频率一致的基础上将系统等值聚合为一个单机带负荷模型，其结构如图1所示。

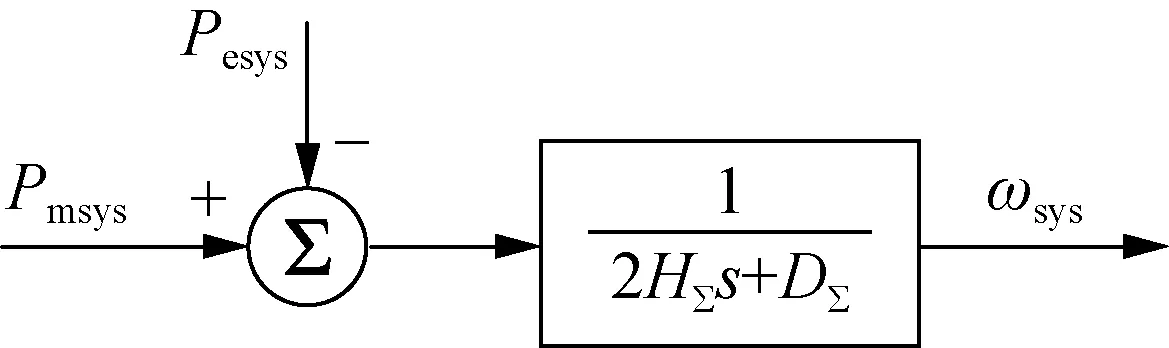
图1 SFR模型框图

其中，Pesys为等值电磁功率；Pmsys为等值机械功率；H∑为等值转子惯性时间常数；D∑为等值阻尼系数；ωsys为等值转子转速。由于对系统进行了等值化简，SFR模型分析功率事故下电网惯量响应情况时具有较高的计算效率，在低频减载整定方面应用广泛。

然而，随着电网规模的扩大和机组的大容量集中接入，惯量响应不仅受扰动大小的影响，还与扰动的位置有关，并体现在频率变化率和频率最低点等指标的空间差异性中[21-22]。频率变化率是惯量响应的重要指标，一方面表征频率变化的速率，另一方面也解释了系统频率变化与系统发生的事故大小和系统的惯性大小的关系。RoCoF的计算一般为选择故障发生后的100～500 ms内[23]，其计算公式如下：

(1)

式中：f为系统频率；w为系统角速度。

以IEEE 39节点系统为例(详见第4节)，在相同大小功率扰动下，分别采用SFR模型和时域仿真法计算惯量响应的频率变化率，结果如图2所示。对比可见，SFR模型不能考虑空间因素影响，而实际电网的频率变化率随扰动位置的不同而变化，存在明显的空间差异性。尤其在低惯量区域，实际的频率变化率与SFR模型计算结果相差较大，如果保护装置仍按照SFR模型进行整定设计，可能会造成保护的误动和拒动[24]。虽然时域仿真法可以详细计算惯量响应频率状态量的数值解，可体现空间分布特征，但耗时费力，对模型精度、系统规模有一定限制。

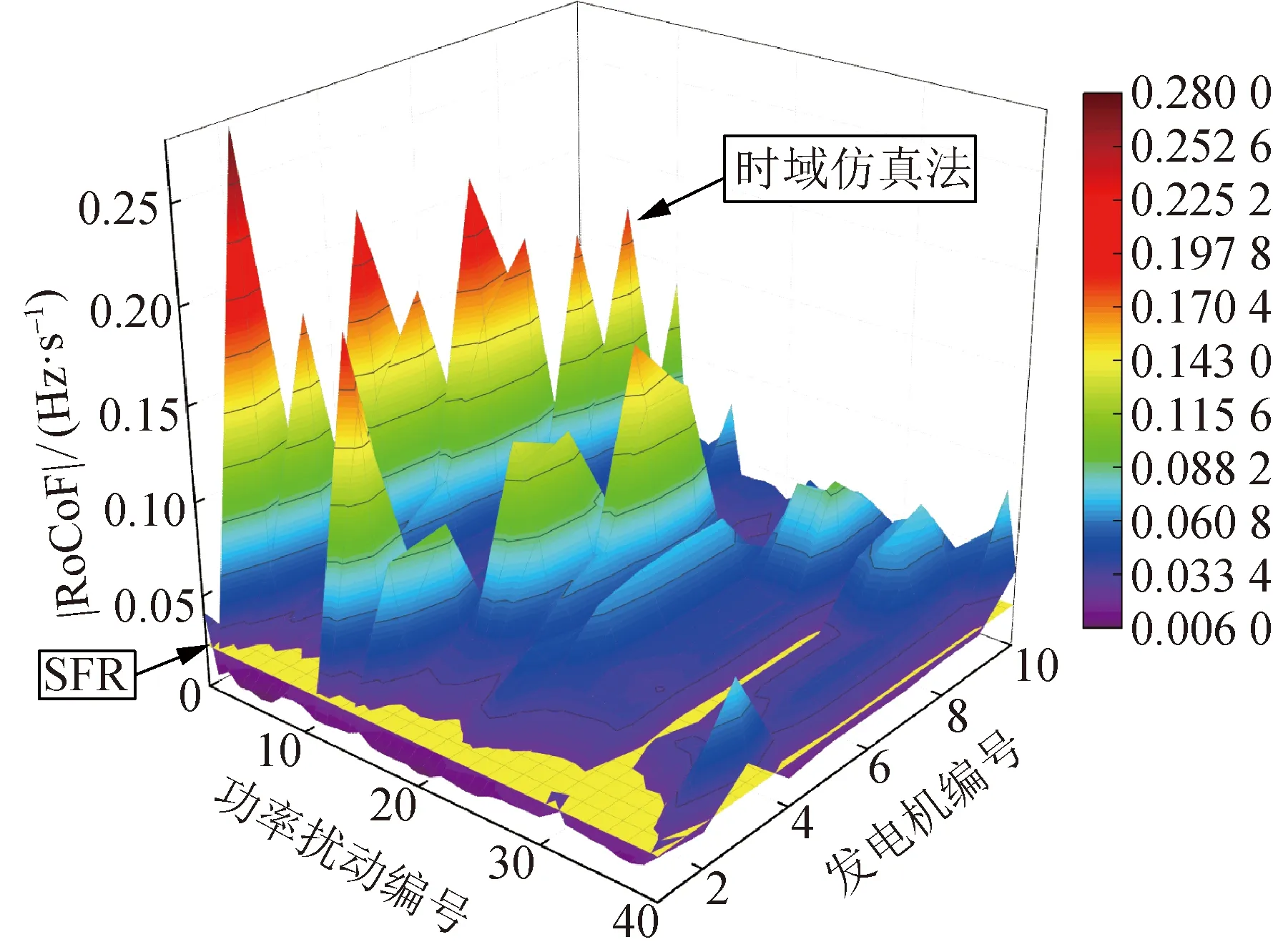
图2 惯量响应空间差异性

1.2 基于直流潮流的惯量响应建模

为快速且准确地评估功率事故后电力系统的惯量响应，文中忽略了无功-电压的耦合影响，并基于以下假设对电力系统惯量响应进行建模分析[25-27]：

1)系统不存在功角和电压不稳定问题，进而将模型线性化。

2)高压输电网电抗远大于电阻，系统有功潮流主要由电压相角决定，忽略电压幅值变化及发电机调压器的影响。

3)系统惯量响应发生于扰动初始时刻，此时发电机调速器尚未作用，忽略发电机调速器，采用经典发电机模型。

基于上述假设，为保留网络拓扑结构并简化计算，采用直流潮流模型描述系统网络方程，经线性化后可有：

(2)

式中：ΔPG、ΔPD分别为发电机、负荷节点注入功率变化量列向量；BGG、BGD、BDG和BDD分别为以支路导纳建立的节点导纳矩阵的子阵；δ、θ分别为发电机、负荷节点电压相角变化量列向量。

同时，为与直流潮流网络模型保持一致，进一步忽略发电机定子电阻并假定发电机内电势和机端电压维持1 pu恒定，线性化的发电机转子运动方程为：

(3)

式中：Δδi为发电机转子角变化量；Δωi为发电机转子转速变化量；ω0为转子转速额定值；ΔPmi为原动机机械功率变化量；ΔPGi为发电机电磁功率变化量；Di为发电机阻尼系数；Mi为发电机惯性时间常数。

综合式(2)与式(3)，可以得到多机系统频率动态过程的状态矢量方程：

(4)

式中：J=BGG-BGDBDD-1BDG；L=-BGDBDD-1；EN为N阶单位矩阵；M为发电机惯性时间常数的对角矩阵。

发生负荷突变或联络线有功功率突变等负荷功率扰动时，功率不平衡量按照同步功率系数矩阵L分配给各发电机组，各发电机组按照分配的功率与自身惯量进行惯量响应。由于扰动初始时刻发电机的功角和转速不发生突变，有Δδ=0，Δω=0，惯量响应初期阶段系统内各机组频率变化率的数学表达式为：

(5)

与SFR模型相比，基于直流潮流的电力系统惯量响应模型保留了电网拓扑结构，可以分析功率扰动位置、网络拓扑结构和机组惯量大小等空间因素的影响，可以体现惯量响应的空间差异性。同时，由于忽略了无功-电压动态的耦合影响，重点关注惯量响应的频率变化和与频率变化关系密切的有功功率变化，相比时域仿真可以大幅减少用时，提升分析效率。

2 基于RGA的惯量响应分析方法

根据上述分析，多机系统惯量响应的数学模型本质为多输入多输出的系统，受网络拓扑结构的影响，电力系统惯量响应模型输入的功率扰动向量与输出的惯量响应频率变化率之间存在复杂的相互作用。

为研究多输入多输出(multi-input and multi-output，MIMO)系统控制回路之间耦合程度，BRISTOL于1965年提出相对增益矩阵的理论[28]。如图3所示的m输入n输出系统中，输入uj与输出yi间的相对增益λij可定义为开环增益与闭环增益的比值：

图3 多输入多输出系统框图

(6)

式中：分子为其他控制回路开路，只改变输入量uj时，uj到yi通道的静态开环增益；分母为其他输出量yi(k≠i)均不变时，uj到yi通道的静态闭环增益。

MIMO系统的相对增益矩阵通常通过式(7)所示的矩阵运算方法计算得到：

Λ=G(0)⊗(G(0)-1)T

(7)

式中：G(0)为系统传递函数的静态增益矩阵；上标T为矩阵的转置；运算符⊗为矩阵的Hadamard乘积。

当n=m时，系统为方形系统，且相对增益矩阵为方阵，G(0)-1为G(0)的逆矩阵；当n≠m时，系统为非方系统，相对增益矩阵为非方矩阵，G(0)-1为G(0)的广义逆矩阵。

在分析多个控制回路之间的相互作用时，相对增益矩阵Λ具有以下主要特性[29]：

1)RGA任意行的元素之和等于1，即

(8)

2)RGA任意列的元素之和介于0到1之间，即

(9)

3)RGA中相对增益λij的大小反映了输入uj与输出yi之间的耦合程度，相对增益λij越接近1，则该通道耦合程度越大。

与分析控制系统中多个控制回路之间的相互作用类似，使用相对增益矩阵来量化评估惯量响应的空间耦合特征。根据非方系统相对增益矩阵的定义，以式(5)中的[M-1M-1L]作为传递函数的静态增益矩阵，计算m机n节点系统惯量响应频率变化率与有功功率扰动之间的相对增益矩阵，如下所示：

Λm×(m+n)=[M-1M-1L]⊗[[M-1M-1L]-1]T

(10)

为便于分析不同对象之间的耦合特性，将相对增益矩阵Λm×(m+n)进行分块，如图4所示。

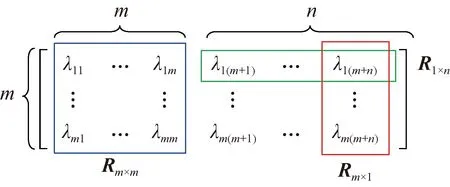
图4 相对增益矩阵

其中，Rm×m描述了发电机与原动机输出功率扰动之间的耦合关系，Rm×1描述了某一节点功率扰动与各发电机的耦合关系，R1×n描述了某一发电机与各节点功率扰动的耦合关系。

3 惯量响应空间耦合特征分析

3.1 原动机空间耦合特征

遭受原动机功率扰动后的惯量响应阶段，系统电磁功率分布不发生突变，原动机功率扰动带来的功率不平衡量仅作用于该发电机组，并引起其自身发生惯量响应，其他发电机组不发生惯量响应。

相应的，此时原动机功率扰动与发电机惯量响应之间的相对增益矩阵为对角矩阵，如式(11)所示。根据相对增益矩阵理论，对角元素表示该原动机功率扰动仅与该发电机自身存在强耦合关系，对角线外的零元素表明该原动机功率扰动与其他机组的惯量响应无耦合关系。

Rm×m=diag(λ11,λ22,…,λmm)

(11)

3.2 发电机空间耦合特征

对于发电机组而言，相对增益矩阵行向量元素的大小可以表征该发电机与各负荷节点之间的耦合程度，如式(12)所示。遭受相同大小的功率扰动时，扰动发生节点对应的相对增益越大，发电机组惯量响应频率变化率的幅值越大，体现了该发电机组惯量响应的空间耦合特征。

(12)

低惯量发电机组抵御功率扰动引起频率变化的能力较弱，是系统频率稳定的薄弱区域。当扰动发生在与惯性薄弱区域强耦合的负荷节点时，低惯量发电机组容易产生较大的频率跌落速度，导致一次调频响应前频率跌落幅值较大。

因此，可以借助相对增益矩阵识别低惯量发电机组的强耦合区域，通过在该区域配置FFR资源，通过快速的有功功率注入以减缓扰动后频率的跌落速度，避免惯性薄弱区域出现较大的频率跌落幅值而引发低频率减载动作。与SFR模型相比，借助相对增益矩阵考虑空间耦合特征，可以提高FFR资源的运行效率，进而降低投资成本。

3.3 负荷节点空间耦合特征

对于负荷节点而言，相对增益矩阵列向量元素的大小可以表征该负荷节点与各发电机之间的耦合程度。由于相对增益矩阵的行向量之和均为1，在纵向比较列向量表示的负荷扰动的耦合情况时，需要对相对增益按照惯量大小进行修正，如下所示：

R′m×1=M-1×[λi,1…λi,m]，i∈[m+1,m+n]

(13)

修正后矩阵列向量中元素和越小表明该节点与发电机组的耦合程度越小，即遭受相同大小的功率扰动时，电力系统惯量响应的整体频率变化率越小，系统对该节点的惯量支撑能力越强，体现了负荷节点的惯量响应空间耦合特征。

风电、光伏等新能源出力具有较强的随机性、波动性和间歇性，是电网常见的功率扰动源，给电网频率稳定带来挑战。借助相对增益矩阵可以识别出系统惯量支撑能力较强的节点，选择将其作为新能源的接入位置，有助于减少功率扰动对系统频率稳定的影响，降低系统一次调频压力，提高系统对新能源的消纳水平。

4 仿真验证

4.1 仿真系统介绍

以IEEE 39节点系统为例，验证所提基于相对增益矩阵的惯量响应空间耦合特征分析方法的正确性与有效性。该系统包含10台同步机组、34条线路和39个负荷节点，系统电压等级为345 kV，基准容量为100 MV·A，如图5所示，网络和元件参数详见文献[29]。

图5 IEEE 39节点系统

4.2 原动机空间耦合特征仿真分析

为验证发电机惯量响应与原动机功率扰动之间的耦合关系，以6号发电机组为例，在时域仿真中使其原动机机械功率突减至潮流稳态值的90%，计算各发电机组惯量响应初始阶段的RoCoF，并与相对增益矩阵子矩阵Rm×m元素进行对比，结果如图6所示。

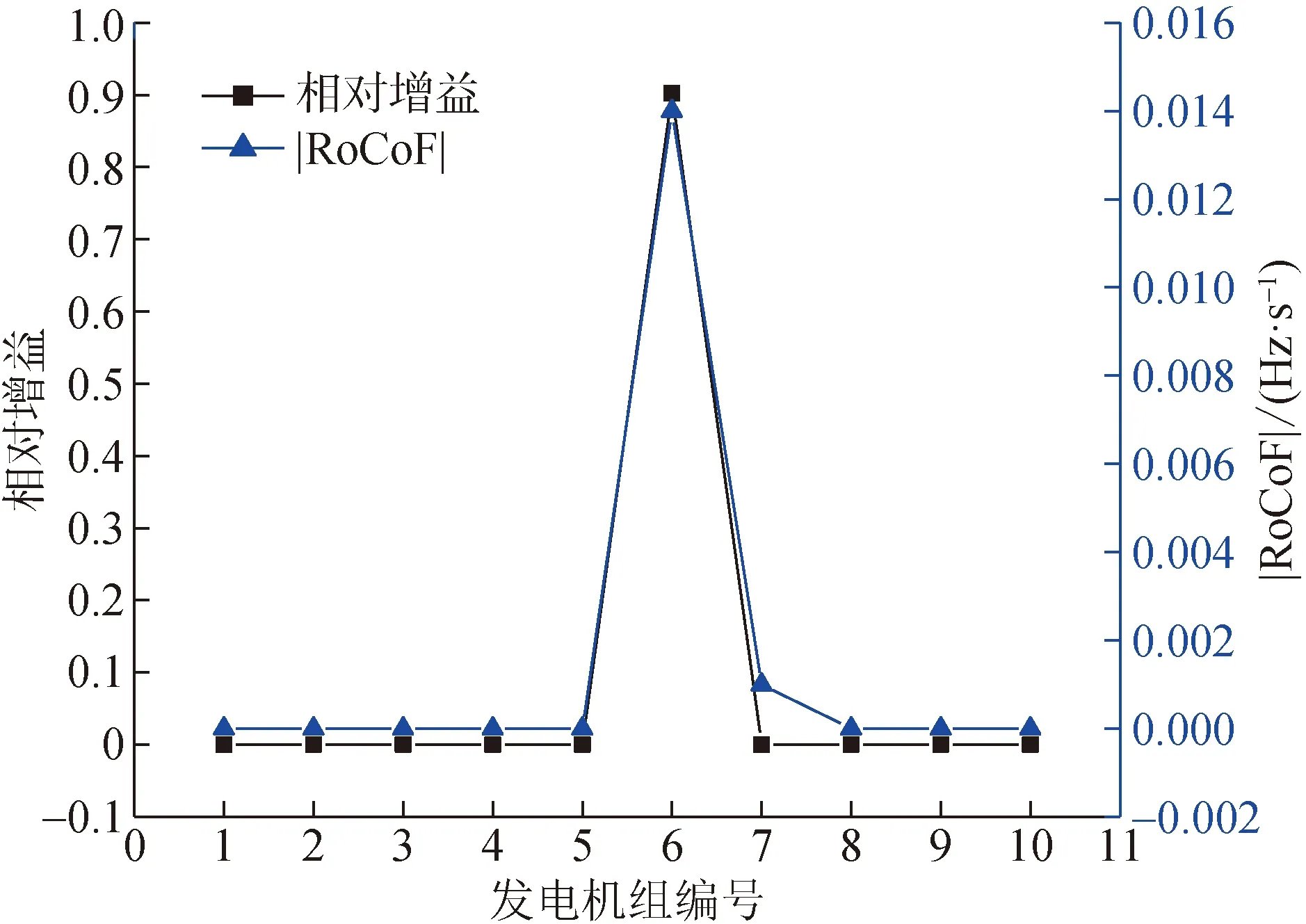
图6 原动机空间耦合特性

对比可见，除6号发电机组外，其余发电机的RoCoF和子矩阵Rm×m元素几乎为0。仿真结果表明，在惯量响应初始阶段，仅施加了原动机功率扰动的发电机自身频率发生变化，其余发电机组频率无明显变化，原动机功率扰动下的惯量响应相互独立，体现出该原动机惯量响应的空间耦合特征。

4.3 发电机空间耦合特征仿真分析

为验证发电机惯量响应与不同负荷功率扰动之间的耦合关系，以1号发电机为例，在时域仿真中分别对各负荷节点施加50 MW的有功功率突增量，计算扰动后1号发电机组惯量响应阶段的RoCoF，并与RGA子矩阵R1×n元素进行对比，结果如图7所示。

图7 发电机空间耦合特性

仿真结果表明，发电机惯量响应的频率变化率随着负荷扰动发生位置的变化而不同。RGA子矩阵R1×n元素越大，表征发电机与相应负荷节点的耦合程度越大，发电机惯量响应的RoCoF也就越大，体现出该发电机组惯量响应的空间耦合特征。

4.4 负荷节点空间耦合特征仿真分析

为验证负荷功率扰动与不同发电机惯量响应之间的耦合关系，根据式(13)计算的修正后RGA子矩阵R′m×1列元素之和，如图8(a)所示。其中，1、13、22、31、39等节点的RGA子矩阵R′m×1列元素较小，可认为是系统惯量支撑较强的节点。同时，在时域仿真中分别对不同负荷节点施加50 MW的有功功率突增量，计算扰动后各发电机组惯量响应的RoCoF，结果如图8(b)所示。

图8 负荷节点的空间耦合特性

对比可见，在发生相同大小的负荷功率扰动下，当扰动位置为通过相对增益矩阵识别的惯量支撑较强的节点时，系统的RoCoF整体更小，此时系统具有更好的频率稳定性。仿真结果表明，RGA子矩阵R′m×1体现了负荷节点对惯量响应的空间耦合特征，可用于识别系统惯量支撑较强的负荷节点，有助于指导新能源的接入位置选择。