基于特征加权Stacking集成学习的净负荷预测方法

鲍海波，吴阳晨，张国应，李江伟，郭小璇，黎静华

(1.广西电网有限责任公司南宁供电局，南宁市 530031；2.广西电力系统最优化与节能技术重点实验室(广西大学)，南宁市 530004；3.广西电网有限责任公司电力科学研究院，南宁市 530023)

0 引 言

随着大规模新能源尤其是分布式新能源在用户侧接入电网，通常采用实际用电负荷减去新能源出力后的负荷功率(以下称为“净负荷”)进行预测、调度方面的研究[1]。准确预测净负荷对于新型电力系统的规划、优化运行和控制具有重要意义。

目前，已有不少学者对净负荷预测开展了研究工作。根据是否组合多个预测模型来进行预测，现有净负荷预测方法可分为单一预测方法和集成预测方法[2-3]。

净负荷的单一预测方法主要包括时间序列预测法、神经网络预测法、支持向量机预测法等。文献[4]采用差分整合移动平均自回归模型(autoregressive integrated moving average model, ARIMA)建立净负荷预测模型，利用自适应预测策略优化模型参数，并通过仿真分析证明该方法适用于含风电的净负荷预测。然而，由于ARIMA为线性预测模型，其挖掘净负荷非线性变化规律的能力有限。文献[5]提出一种基于经验模态分解和深度信念网络的预测方法，首先将净负荷时序数据分解为频率、幅值不一的时序分量，然后用深度信念网络建立各时序分量的预测模型。该方法仅考虑净负荷的时序规律，忽略了气象等因素对净负荷的影响，因此预测精度有限。文献[6]提出基于最小二乘支持向量机(least squares support vector machine，LSSVM)的预测方法，适用于净负荷样本数量较少的情况。然而，由于LSSVM的网络结构相对简单，其面对特性复杂的净负荷时预测能力有限。

由以上分析可知，单一预测方法在净负荷预测中具有一定的局限性。这是因为单一预测方法仅从某一特定角度挖掘负荷的变化规律，而净负荷具有强波动性和不确定性，单一方法通常难以对净负荷进行全面、准确的建模[5]。针对单一预测方法的不足，有学者提出了集成预测方法。集成预测方法通过集成学习理论将多个预测模型进行结合，综合了不同模型的预测优势，通常可获得比单一预测模型更优越的预测性能。

负荷预测中比较成熟的集成预测方法主要有Boosting方法和Stacking集成方法。文献[7]提出了Boosting集成原理的XGBoost预测模型，实现了对日高峰负荷的准确预测。Boosting方法属于串行集成学习算法，其对同一类算法进行多次迭代训练，每次迭代结束时产生一个学习器，由此获得多个学习器。因此，Boosting方法的学习器之间存在较强的依赖关系，导致该方法在预测任务中的泛化能力有限。

Stacking集成方法则采用并行学习方式，采用不同类型算法(称为“初级学习器”)获得初步预测值，并采用元学习器进一步优化初步预测值，得到最终的预测结果。文献[8]提出一种基于多模型融合Stacking集成学习方式的负荷预测方法，采用长短期记忆神经网络(long short-term memory, LSTM)、梯度决策树、随机森林、支持向量机等作为集成学习的初级学习器，然后通过元学习器对初级学习器的预测结果进一步优化。该方法充分发挥各个模型优势，对常规负荷的预测效果良好。文献[9]构建了基于卷积神经网络(convolutional neural networks, CNN)和LSTM的Stacking集成负荷预测方法，兼顾了CNN和LSTM网络模型优点，预测效果较好。

然而，文献[8-9]均采用传统的Stacking集成学习框架，在模型训练过程中将不同初级学习器的输出结果平均加权以构造元学习器的训练数据。换言之，传统Stacking集成方法的训练过程不考虑初级学习器之间的差异性。当某一初级学习器的预测误差较大时，将给元学习器的训练过程引入较大的误差特征，进而影响到整体模型的预测准确性。

基于以上分析，本文提出一种改进的Stacking集成净负荷预测方法。首先，通过对不同算法预测性能的差异性分析，优选出LSTM模型[10-12]、随机森林树(random forest，RF)[13-14]、Elman网络[15]、LSSVM[16-18]作为Stacking集成学习的初级学习器。其次，针对传统Stacking集成学习训练过程因忽略初级学习器差异性导致的问题，根据预测效果对初级学习器赋予相应的权值，从而对初级学习器的预测误差进行修正，一定程度上摒弃各个算法中预测效果较差的部分，最终提升整体预测精度。最后，为了检验本文方法在不同场景下的预测效果，分别对周末、晴天、多云、多雪、多雨等场景下的净负荷进行预测。算例分析结果表明，本文所提出的集成预测方法相较于单一预测方法和传统Stacking集成预测方法具有更高的精度，而且能适应晴天、多云、多雨等不同环境场景。

1 Stacking集成预测原理

Stacking集成预测的框架如图1所示，包含两层预测模型，第一层预测模型称为初级学习器，第二层预测模型称为元学习器。Stacking集成预测方法首先将原始数据输入到各初级学习器中，获得初级学习器的预测结果。然后将初级学习器的预测结果作为元学习器的输入，得到最终的预测结果。Stacking集成预测方法通过对多个初级学习器的集成，结合了不同学习器的优势，使预测模型具有较强的泛化能力；进一步采用元学习器优化初级学习器的输出结果，提升整体的预测精度[19]。

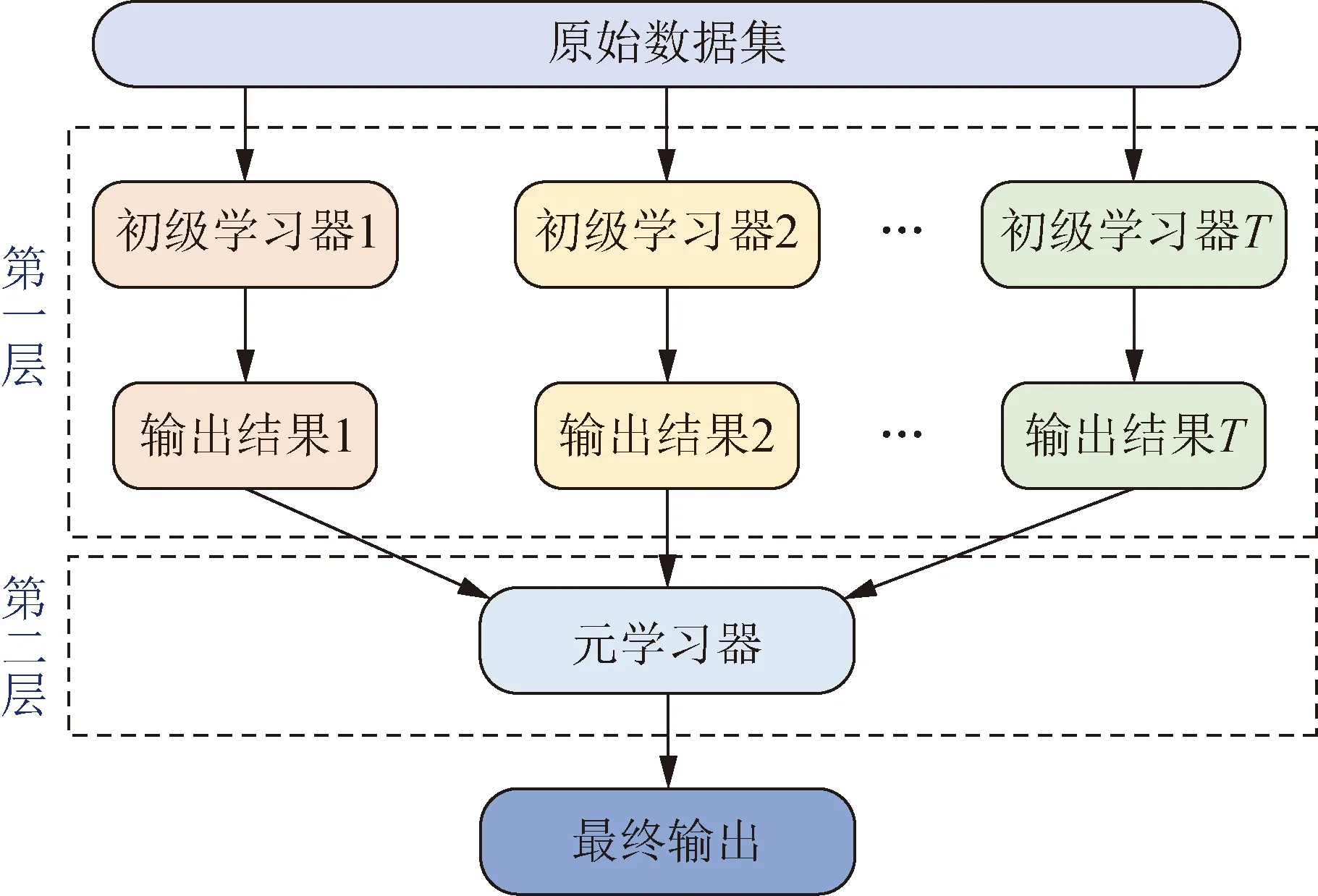
图1 Stacking集成预测框架过程

在Stacking集成预测的模型训练过程中，通常采用k折交叉验证法进行数据划分和模型训练，以减少出现过拟合的风险[20]。k折交叉验证法的流程如图2所示。首先，将原始数据集D平均划分为k个互斥子集，分别为D1,D2,…,Dk。然后，分别选择其中k-1个子集的并集作为训练集，余下的1个子集作为测试集，构造初级学习器的训练集和测试集。这样可获得k组训练集和测试集。对于Stacking集成预测中的每一个初级学习器，都采用这k组训练集和测试集进行学习器的训练和测试，并获得k个测试结果S1,S2,…,Sk。这一过程称为“交叉验证”。

图2 k折交叉验证流程图

以上是基于k折交叉验证法的Stacking集成预测模型训练过程。值得注意的是，k折交叉验证法的效果很大程度上取决于k的取值。k常用的取值有5、10、20等。

2 基于特征加权的改进Stacking集成预测方法

2.1 传统 Stacking集成算法的不足分析

已有研究表明，元学习器训练数据集的属性特征对于Stacking集成预测的性能有较大影响[21]。元学习器输入数据的误差成分越少，其训练效果则越好，Stacking集成预测的精度也越高[22]。由第1节可知，传统的Stacking集成预测方法在构造元学习器的训练样本时，直接将多个初级学习器的输出结果作为元学习器的输入。然而，各个初级学习器的性能不尽相同，当某些初级学习器的输出结果误差较大时，直接构造输入样本将给元学习器的训练过程引入较大的误差特征，进而影响到整体模型的预测准确性。

针对该问题，本文提出一种特征加权法用于改进传统Stacking集成算法的不足。根据各学习器自身的预测精度，为初级学习器生成的训练数据赋予相应的权值，再代入元学习器进行训练。所提出的改进方法对各初级学习器的预测误差进行了修正，从而在一定程度上摒弃各个算法中预测效果较差的部分，生成更有利于元学习器训练的数据集。

2.2 Stacking集成预测的特征加权改进

本文提出的基于特征加权的Stacking集成方法，其核心在于根据各初级学习器的预测效果赋予不同的权值。具体计算方法如下：

1)选取均方根误差(root mean square error, RMSE)作为评估初级学习器预测精度的指标。RMSE公式如下：

(1)

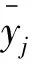
2)将数据集按8∶2划分为训练集和验证集。采用训练集对各初级学习器进行训练，并计算各个初级学习器在验证集上的均方根误差。对均方根误差进行标准化处理，标准化公式为：

(2)

式中：wl为第l个初级学习器的权重，l=1,2,…,T；T为初级学习器的个数；ERMSE,l为第l个初级学习器的均方根误差；ERMSE,h为第h个初级学习器的均方根误差。

(3)

式中：Si,1,Si,2,…,Si,T分别为T个初级学习器在第i折交叉验证中的输出；w1,w2,…,wT分别为T个初级学习器的权重。

2.3 Stacking集成预测学习器的优化选择

Stacking集成预测方法中学习器的选择直接决定集成预测效果。对于初级学习器的选择，应遵循“好而不同”的原则，即各初级学习器要有较高的预测精度，同时各学习器间应具有差异性，即各学习器由不同的算法生成[2]。这是因为预测能力较强的模型有助于提升整体的预测精度，而模型之间差异性较大，有助于从更广泛的角度来学习数据中蕴藏的规律，从而提升整体预测方法的泛化能力。

据此，本文基于对不同模型预测能力和模型差异性的分析，优选出Stacking集成预测的初级学习器。其中，采用Pearson相关系数对各模型的误差关联性进行计算，以此分析不同初级学习器的差异性。各模型预测能力和差异性的分析过程将在本文第3.3节中具体讨论。最终，本文优选出LSTM算法、RF算法、Elman网络和LSSVM算法作为Stacking集成预测的初级学习器。

其中，LSTM是一种深度循环神经网络，可以学习长时间尺度的时序特性，在负荷预测领域得到广泛应用，其建模过程见参考文献[11]。RF是结合决策树和Bagging集成的一种预测方法，具有抗噪力和适应力强等优点，被广泛应用于各领域，其实现过程见参考文献[13]。Elman网络是一种具有局部记忆单元和局部反馈连接的神经网络，能够挖掘数据中的短期时序特性并进行预测，其建模过程见参考文献[15]。LSSVM在解决小样本、非线性及高维度的预测问题上具有独特优势，在负荷预测中有良好的实践效果。LSSVM算法实现过程见参考文献[16]。

对于Stacking集成预测的元学习器，本文选择训练高效、非线性拟合能力强的LSSVM作为元学习器，对初级学习器的预测结果做进一步的优化。

2.4 基于特征加权Stacking集成方法的净负荷预测步骤

本文提出的基于特征加权Stacking集成的净负荷预测方法流程如图3所示。

图3 基于特征加权Stacking集成净负荷预测方法

基于特征加权的Stacking集成净负荷预测方法的主要步骤如下：

1)对原始数据进行归一化处理，将归一化后数据划分为训练集和测试集。

2)采用训练集，对Stacking集成预测的各个初级学习器进行训练，并计算各个初级学习器的均方根误差。根据式(1)、式(2)，计算出各个初级学习器的特征权重。

3)取k=5，采用5折交叉验证法对数据集进行划分，并对Stacking集成预测的模型进行训练。将5折交叉验证中初级学习器的输出结果，按式(3)进行特征加权，获得含特征加权的元学习器训练数据集。

4)使用含特征加权的数据集对元学习器进行训练。训练过程中，元学习器LSSVM的输入为图3中各个权值与预测结果乘积的并集，输出为图3中未使用数据集的并集。

5)对于待预测数据集，将各初级学习器的预测结果按式(3)进行加权，输入到训练好的元学习器中，输出最终的预测结果。

3 仿真分析

3.1 仿真说明

本文采用德国TENNET区域2016年的净负荷数据和气象数据进行仿真分析(采样周期为1 h)。其中，净负荷数据由用电负荷减去光伏发电功率得到，数据来源见文献[23]。气象数据来源见文献[24]。预测模型的输入特征量包括时间、降雨量、温度、表面辐照度、大气辐照度、降雪量、云量、气压。

为了验证所提出的基于特征加权Stacking集成学习方法的有效性和先进性，采用以下方法作为对比方法：1)单一预测模型，包括LSTM网络、RF模型、Elman网络、RBF神经网络、BP神经网络、LSSVM模型、决策树；2)无特征加权的传统Stacking集成学习方法。

为了检验本文方法对不同场景下净负荷预测的适应性，设置了如表1所示的仿真场景。其中，连续1个月的预测场景用于检验本文方法的整体预测水平。同时，考虑到日类型、降雨量、降雪量、云量等气象因素对净负荷的影响[1]，分别对周末、晴天、多云、多雪、多雨等5种类型的净负荷进行预测。其中，周末区别于工作日，用户用电行为具有特殊性，因此采用周末预测场景检验本文方法对特殊日类型场景下的预测效果；设置晴天、多云、多雪、多雨等天气场景，则是为了检验本文方法对不同天气场景下的净负荷预测效果。通过设置6种类型的净负荷预测场景，对比分析不同情况下各个预测方法的预测效果，以检验本文方法的适应性和有效性。

表1 仿真场景

将2016年1月1日至11月30日的净负荷及相关气象数据作为训练样本集，用于确定各初级学习器的权重系数以及对模型进行训练。不同仿真场景下测试集划分如下：在连续1个月净负荷预测的仿真场景中，测试集为整个12月份的净负荷相关数据；在周末净负荷预测场景中，测试集为12月10日、11日(分别为周六、周日)的数据；在晴天净负荷预测场景中，测试集为12月7日、8日的数据；在多云净负荷预测场景中，测试集为12月2日、16日的数据；在多雪净负荷预测场景中，测试集为12月19日、20日的数据；在多雨净负荷预测场景中，测试集为12月1日、25日的数据。其中，以上不同天气类型下测试集对应的日期由气象预报确定。

采用平均绝对百分比误差(mean absolute percentage error, MAPE)作为预测误差指标[25]，其计算公式为：

(4)

3.2 单一模型的预测结果分析

为说明本文优选Stacking集成预测初级学习器的过程及其合理性，本节首先对不同单一模型的预测性能和差异性进行分析。

选择LSTM、RF、Elman网络、RBF网络、BP网络、LSSVM、决策树等7种单一预测模型，作为初级学习器的待选项，设计实验对各个初级学习器单独预测的结果进行比较。将净负荷数据按5折交叉验证的方式进行划分，产生5组训练集和测试集。各单一预测模型在5个测试集上的MAPE数值如表2所示。

表2 各单一预测模型的MAPE

进一步，为了分析各个预测模型的预测差异性，计算各个模型预测误差的Pearson相关系数，结果如图4所示。

由表2可知，LSTM模型、LSSVM模型和RF模型的预测精度相对较高。由图4可知，各模型的误差相关性普遍较高，这是由于各模型的学习能力较强，训练所得的训练误差分布也较为相似引起的。其中，Elman网络、RBF网络和BP网络均属于神经网络算法，虽然从预测精度上来看，RBF网络的预测性能优于Elman网络和BP网络，但是Elman网络与其他算法相关性较低。综上考虑，最终选择LSTM模型、Elman网络、RF模型、LSSVM模型作为Stacking集成预测的初级学习器。

图4 各模型预测误差的相关性分析

3.3 不同仿真场景的结果分析

3.3.1 连续1个月的净负荷预测结果分析

表3为不同预测方法对2016年12月整月的净负荷预测误差统计结果。从预测误差平均值来看，本文方法的EMAPE为6.83%，优于BP网络(EMAPE为7.43%)、LSSVM模型(EMAPE为7.15%)、RF模型(EMAPE为7.79%)和LSTM模型(EMAPE为8.33%)，证明了本文的集成预测方法比单一预测方法具有更高的预测精度。

表3 不同预测方法对12月净负荷预测的MAPE

无加权Stacking集成方法的EMAPE为7.28%，其预测精度高于BP网络、LSTM、随机森林算法，而低于Elman神经网络和LSSVM算法，表明直接采用无加权Stacking集成方法的效果未必优于所有单一预测方法。同时，本文方法优于无加权Stacking集成方法，表明对初级学习器进行特征加权可以提高Stacking 集成预测方法的精度。

图5为不同预测方法对2016年12月不同时间点(24个时刻)的净负荷预测绝对误差百分比统计结果的折线图，所采用的分析数据为12月整月的净负荷预测误差数据。分析不同时间段各预测方法的预测精度，可发现对于所有预测方法，06：00—16：00时间段内预测误差相对于其他时段更大。这是因为该时间段内存在光伏发电，净负荷的随机性和波动性增强，负荷预测难度增大。同时可发现，该时间段内本文方法预测精度高于与其他方法。

图5 不同预测方法对12月24 h净负荷预测的MAPE

3.3.2 对周末净负荷预测结果的分析

在周末，用户用电的模式通常与工作日不同。因此周末净负荷的变化规律往往更难把握，预测难度更大。图6展示了不同预测方法对12月份2个周末日的净负荷预测结果。

由图6可看到，相比于Elman网络、BP网络、RBF网络、LSSVM算法、RF模型、决策树、LSTM模型、无加权Stacking集成方法，本文方法的预测曲线更接近于实际净负荷曲线。

进一步统计不同预测方法对周末日的净负荷预测误差。其中，本文方法(EMAPE为6.23%)和无加权Stacking集成方法(EMAPE为6.25%)预测精度高于Elman网络(EMAPE为7.04%)、BP 网络(EMAPE为8.87%)、RBF网络(EMAPE为9.75%)、LSSVM模型(EMAPE为6.69%)、RF模型(EMAPE为6.34%)、决策树模型(EMAPE为10.18%)、LSTM模型(EMAPE为7.80%)等单一预测方法，表明对于周末净负荷的预测，集成预测方法比单一预测方法更有优势。同时可看到，本文方法的预测精度高于无加权Stacking集成方法，表明本文方法更适合用于周末的净负荷预测。

3.3.3 对晴天净负荷预测结果的分析

图7为不同方法在晴天条件下的2天净负荷预测曲线。观察图7中的实际净负荷曲线可发现，在中下午时段净负荷曲线向下凹陷，峰谷差变大，负荷爬坡明显。这是因为中下午时段光伏出力较大的缘故。

观察图7中的各预测曲线可发现，Elman网络、BP网络、RBF神网络、LSSVM算法、RF、决策树和LSTM的预测曲线与实际净负荷曲线偏差较大。无加权Stacking集成方法和本文方法的预测曲线更接近于实际净负荷曲线。

图7 不同预测方法对晴天净负荷的预测结果

表4为各个预测方法对晴天净负荷预测的平均绝对百分比误差。由表4中数据可以看出，本文方法(EMAPE为6.13%)和无加权Stacking集成方法(EMAPE为6.62%)预测精度高于Elman网络(EMAPE为6.78%)、BP神经网络(EMAPE为7.86%)、RBF神经网络(EMAPE为7.78%)和LSSVM算法(EMAPE为7.29%)、随机森林树(EMAPE为6.95%)、决策树(EMAPE为10.81%)、LSTM(EMAPE为8.57%)。表明Stacking集成预测对晴天净负荷的预测精度更高。

对比表4和表3可发现，对于晴天净负荷预测，本文方法、无加权集成的Stacking、Elman算法、随机森林树算法的预测精度都有所提升。这是因为晴天时光伏出力较稳定，光伏发电对净负荷的影响较小，净负荷的变化规律较容易把握，因此预测精度有所提高。

表4 不同预测方法对晴天净负荷的预测误差

3.3.4 对多云天气净负荷预测结果的分析

图8为不同方法在多云天气下2天净负荷预测曲线。可看到本文方法的预测曲线与实际净负荷曲线最为靠近，表明本文方法可以较为准确地跟踪多云天气下的净负荷变化，实现较高的预测精度。

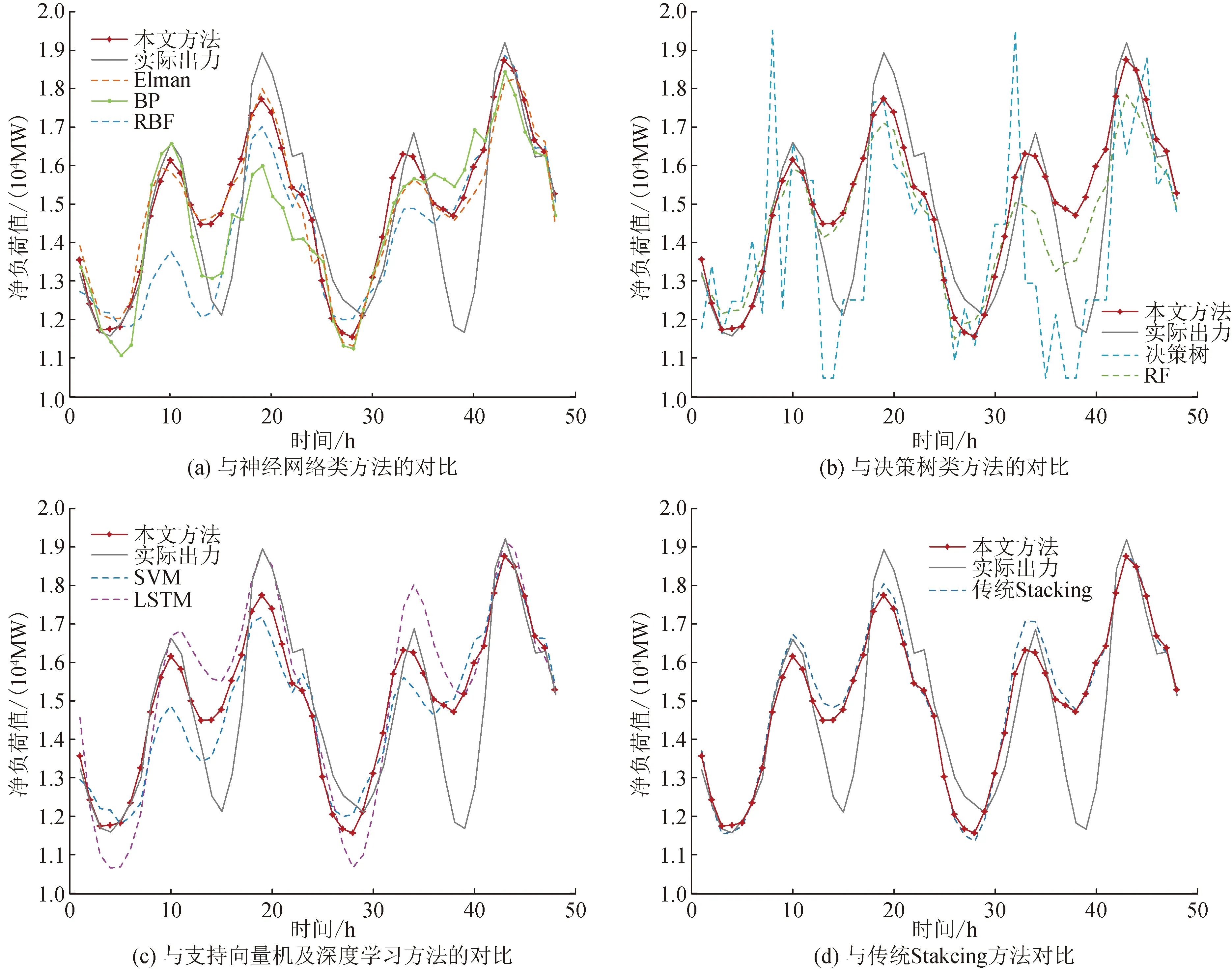
图8 不同预测方法对多云日净负荷的预测结果

表5为各个预测方法对多云净负荷预测的平均绝对百分比误差。由表5可看到，本文方法(EMAPE为2.45%)预测精度高于Elman网络(EMAPE为4.76%)、BP网络(EMAPE为4.23%)、RBF网络(EMAPE为4.11%)和LSSVM算法(EMAPE为3.39%)、RF模型(EMAPE为2.66%)、决策树(EMAPE为6.85%)、LSTM(EMAPE为6.26%)等单一预测方法，同时也高于传统的无加权Stacking集成预测方法(EMAPE为2.53%)。表明本文所提出的基于特征加权的Stacking集成预测方法更适合于多云场景下的净负荷预测。

对比表5和表3可发现，各方法对多云天气净负荷的预测精度高于整月的平均预测精度。这是因为多云天气下光伏出力较少且相对平稳，光伏发电对净负荷的影响较小。此外，多云天气对人类的生产生活影响较小，因此用电负荷模式也会遵循一定的历史规律。综上，多云天气下净负荷的随机性和波动性较低，净负荷预测精度普遍较高。

表5 不同预测方法对多云天气净负荷的预测误差

3.3.5 对多雪天气净负荷预测结果的分析

图9为不同方法在多雪天气下的2天净负荷预测曲线。可看到本文方法的预测曲线与实际净负荷曲线最为靠近，表明本文方法可以较为准确地跟踪多雪天气下的净负荷变化，实现较高的预测精度。表6为各个预测方法对多雪净负荷预测的平均绝对百分比误差。

图9 不同预测方法对多雪日净负荷的预测结果

由表6可看到，本文方法预测精度高于各单一预测模型，也高于传统Stacking集成预测。表明本文所提出的基于特征加权的Stacking集成预测方法更适合于多雪场景下的净负荷预测。

对比表6和表3可发现，各方法对多雪天气净负荷的预测精度高于整月的平均预测精度。这是因为多雪天气的气象因素不复杂，同时光伏出力很小且相对平稳，多雪天气下净负荷的随机性和波动性较低，净负荷预测精度普遍较高。

表6 不同预测方法对多雪天气净负荷的预测误差

3.3.6 对多雨天气净负荷预测结果的分析

图10为不同方法在多雨天气下的2天净负荷预测曲线，可看到本文方法的预测曲线与实际净负荷曲线最为靠近。

图10 不同预测方法对多雨净负荷的预测结果

表7为各个预测方法对多雨净负荷预测的平均绝对百分比误差。可看到，本文方法预测精度高于Elman网络、BP网络、RBF网络和LSSVM算法、随机森林树、决策树、LSTM等单一预测方法，同时也高于Stacking集成预测。表明本文所提出的基于特征加权的Stacking集成预测方法更适合于多雨场景下的净负荷预测。

对比表7和表3可发现，各方法对多雨天气净负荷的预测精度高于整月的平均预测精度。这是由于降雨量较大时，原光伏出力不大的时间段预测精度较高。

表7 不同预测方法对多雨天气净负荷的预测误差

对比不同方法在表6和表7中的预测误差，可发现各方法在表7中的预测误差更高。这是因为多雨的天气不仅会导致气温降低而且伴随着云量变化。此外，人们的生产生活也会受到降雨量的影响，光伏出力的影响因素变得更加复杂，预测难度也相应提高。

4 结 论

准确的净负荷预测对于新能源并网电力系统的规划、优化运行与控制具有重要意义。为了克服单一预测方法的局限性、提升净负荷的预测精度，提出了基于Stacking集成学习的净负荷预测方法。基于模型预测性能及差异性分析，优选出Stacking集成的初级学习器。针对传统Stacking集成学习忽略初级学习器差异性导致的预测精度不高问题，提出了基于特征加权改进的Stacking集成学习预测方法。

基于德国TENNET区域2016年的净负荷数据进行仿真分析，结果表明所提出的基于特征加权Stacking集成预测方法与单一预测方法和传统无加权Stacking集成预测方法相比，具有更高的预测精度，并适合于不同天气条件和日类型的净负荷预测。同时也发现，不同天气条件下的预测精度差别较大。因此，未来将考虑对不同天气类型净负荷分别建立Stacking集成预测模型。