面向动静态混合环境的智能车运动规划方法
2022-08-30齐尧朱彦齐李永乐徐友春
齐尧,朱彦齐,李永乐,徐友春
(陆军军事交通学院,天津 300161)
0 引言
运动规划以获取安全无碰的可行驶轨迹为目标,在智能驾驶汽车、无人作业机器人和服务机器人的智能软件技术中担任着举足轻重的作用。对于动静态混合环境中(如狭窄街道和越野动态场景)的智能车,其运动规划受到动态障碍物的速度维度、静态障碍物形状的非凸性和自身运动学模型的共同约束。
传统的规划方法如仿生学方法、A*和RRT等,未考虑车辆的非完整性约束,所规划路径难以被智能车跟踪。近年来静态环境中的智能车路径规划问题已得到较好地解决[1],动静态混合环境中的运动规划主要有如下挑战:车辆的非完整性约束增加了轨迹求解的复杂度,静态障碍物的不规则形状降低了求解速度,感知、预测和控制结果存在的不确定性要求高频进行重规划,无时间维度的规划结果极大地丧失求解的最优性,增加时间维度后的求解时效性大幅降低,复杂的决策内容(超车、会车和停车避让等)需要融合在运动规划中。
本文将针对动态环境的运动规划方法总结为以下4类:第1类方法将障碍物视为静止,通过快速重规划完成避障[2],即将动态障碍物或其短期预测轨迹视为静态障碍物,确保短期内与其不发生碰撞。该类方法的求解结果缺乏完备性和最优性,无法适应快速变化的场景和需要“停止-等待”的场景[3]。第2类是速度障碍(Velocity Obstacles,VO)方法,Fiorini 等[4]提出以机器人速度矢量为原点建立速度空间,将障碍物和机器人拟合为带有速度矢量的圆,并投影到该相对速度空间内,通过选择安全速度区间的方式进行避障,能够以毫米级的运算速度得到躲避动态障碍物的动作序列。该类方法易出现陷入“死胡同”和频繁抖动的局部最优问题。第3 类是路径-速度解耦规划的方法,首先使用采样、拟合和优化等方式生成静态环境中的安全路径,其次基于可行驶路径建立ST(路径长度-时间)空间对每一动态障碍物做出决策(避让、忽略、超车和停止)[5],以决策为约束条件规划得到速度曲线。这类方法在结构化环境中的适应能力较强,在非结构化场景中需辅以大量的前期决策。第4 类是在三维时空内进行运动规划的方法,以基于搜索和基于采样的方法为主,Ajanovic等[6]在SL空间内加入时间维度,对环境进行大粒度离散,基于搜索的方法在结构化动态环境中得到三维轨迹;Lin 等[7]在XYT空间内通过简化搜索空间和障碍物碰撞检测,为拥挤行人场景内的低速运动(速度不大于1.5 m·s-1)类车机器人提供安全轨迹;Yang等[8]提出RRT(Rapidly-exploring Random Trees)与CBF(Control Barrier Function)结合的CBF-RRT 方法,在凸空间快速采样得到可行轨迹。
在三维时空内进行运动规划能够完备地解决动静态混合环境中的运动规划问题,现有研究大多针对某一特定工况,在动静态混合环境中应用时存在如下问题:针对动态障碍物的方法,难以同时解决任意形状(非凸)静态障碍物的避让问题;多以低速运动的小型机器人(如圆盘机器人和小型轮式机器人)为研究对象,在小范围场景内展开研究。本文面向存在动态障碍物和任意形状静态障碍物的环境,针对以上问题提出一种基于搜索的三维运动规划方法,以解决智能车长期运动规划问题。本文的主要贡献如下:
(1)提出一种基于混合A*的时空规划方法,该方法基于时空栅格同步规划速度和路径,基于舒适性模型设置不同车速下运动基元的转弯半径,采用PMP(Partial Motion Planning)解决搜索周期长的问题,以高频求解得到满足车辆运动学约束的时间-空间轨迹。
(2)使用多圆拟合的方法将车辆转化为线段,在膨胀空间内快速完成静态障碍物碰撞检测;提出时间间隔法对动态障碍物进行时空安全检测,提升求解过程的碰撞检测效率。
(3)构建速度启发式函数,与距离启发式函数共同引导搜索过程,提升在时空栅格中的搜索效率,并将速度启发式的计算方法应用于分析扩展。
1 基于时空栅格的运动基元构建
1.1 搜索空间
本文选择笛卡尔直角坐标系作为搜索空间以适应复杂非结构化环境。在包含平面和时间的空间中,运动规划包含路径和速度两个维度,常用的方式有解耦式和耦合式两类运动规划方法。解耦式方法是在二维平面获取路径,基于路径在ST 空间内进行速度规划,这类方法辅以离散型决策能够保守地应对大多数场景。但如图1 所示的场景却难以有效处理,解耦式的运动规划方法将会导致智能车停在路口,并不能有效规划出图1所示“停车-等待”的运动轨迹。

图1 一种极限场景Fig.1 An extreme scene
本文使用三维坐标系为搜索空间,即在二维直角坐标中增加时间维度作为搜索空间Ω。

式中:q为搜索空间Ω内的点,t为时间,以车辆初始位置为时间原点,单次规划的最长时间为Nt;x、y为笛卡尔坐标系坐标。
将搜索空间离散为时空栅格,处于同一时空栅格内的搜索节点具有相同的索引值。图2(a)为时空栅格中的静态障碍物示意图,图2(b)为动态障碍物在时空栅格中的示意图,不同于静态障碍物,随着时间增加,其在XY平面的位置逐渐发生变化。
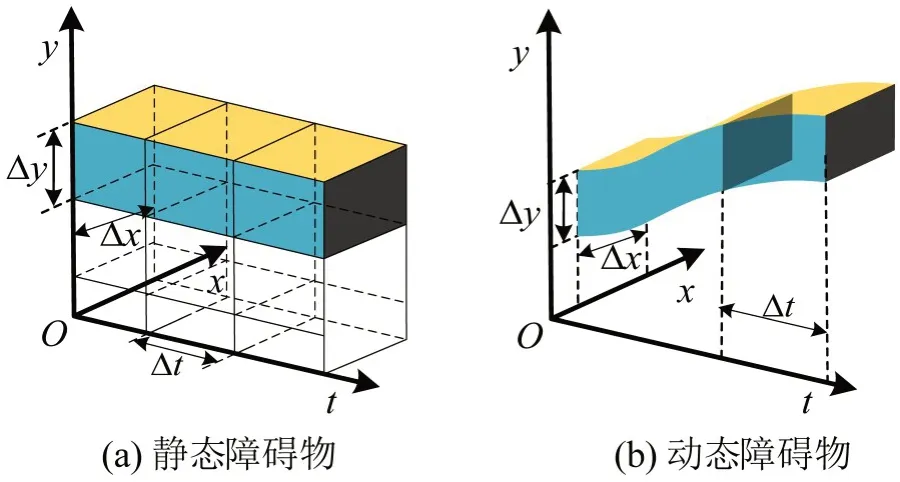
图2 障碍物时空栅格Fig.2 Spatiotemporal grid of obstacles
1.2 车辆运动基元
以u=(a,φ)(a∈[amin,amax],φ∈[-φmax,φmax])表示车辆的纵向控制量a和横向控制量φ,其中,amin、amax为最小、最大加速度,φmax为最大等效车轮转角。以(v,ω)表示行进切线方向的速度v和角速度ω,行驶长度为d,车辆轴距为L,朝向为θ,初速度为v0。假设车轮在平面内做无滑动的纯滚动运动,可得控制量、速度和角速度的运动学关系为

为有效在搜索空间展开运动规划,选择后轴中心点作为车辆的定位点。x=(x,y,θ,v)为车辆状态空间,初始状态x0=(x0,y0,θ0,v0),终点状态xg=(xg,yg,θg,vg)。在搜索时按照固定时间间隔Δt0和最长扩展步长dmax进行单步节点扩展,即
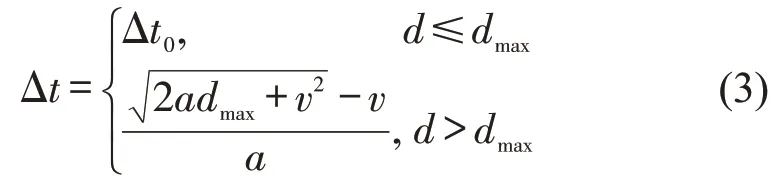
当φ≠0 时,行驶时两个节点之间的状态量差值为

当φ=0 时,车辆保持直行状态,转弯半径为无穷,此时运动学模型与阿克曼转向模型无关,节点间的差值为
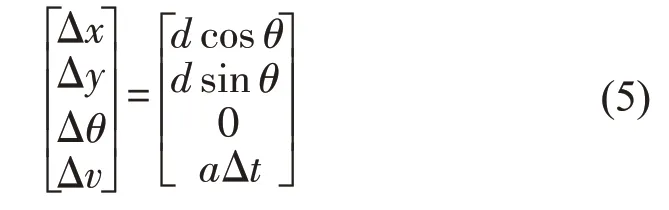
本文通过对控制量u离散的方式生成运动学基元。离散取各个控制量作为输入量,得到XY平面和XT平面的节点ε,如图3所示,图3(a)括号中数值为该位置节点对应的输入控制量。
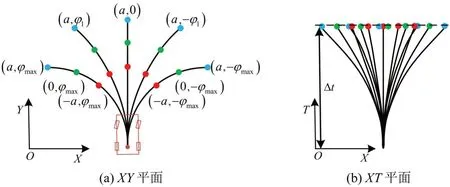
图3 节点扩展方式Fig.3 Node expansion mode
智能车的速度可达每小时数十公里,在不发生侧滑的约束条件下,不同车速对应的最小转弯半径不尽相同,本文提出由“舒适性模型”确定不同速度的最小转弯半径。根据公路线形舒适性评价方法对舒适性模型进行定义:车辆行驶过程中横向加速度低于0.36g时为舒适,其中,g为重力加速度。横向加速度定义为垂直于车辆行驶方向的加速度,是车辆在转弯过程中离心力带来的加速度。其计算方法可用aL=ρv2表示,其中,ρ为车辆转弯半径为r时的曲率,以此确定搜索过程中的节点半径。
2 智能车时空运动规划方法
2.1 实时搜索算法
本文基于混合A*算法[1],采用所提的时空运动基元、启发式函数和碰撞检测方法,按照图4 的算法进行时空搜索。采用哈希表M和优先队列Q对搜索算法进行实现:通过维护高效的哈希表M存储节点及其对应的索引值,可使用节点的索引值在M中快速查找对应的节点;通过优先队列Q存储节点索引值及其f数值,f=g+h,其中,f、g、h分别为总代价、实际代价和启发式代价,优先队列Q中的节点按照f进行升序排列,获取最优节点的索引值,通过索引值在M中快速查找对应的优先节点。智能车在动态行进过程中的目标状态xg难以准确设置,Petti[9]提出PMP:考虑观测范围内的障碍物,获得有效时间内的可行轨迹,不将到达目标点作为唯一搜索终止条件。据此本文使用两类搜索终止条件:第1种为到达目标状态,第2种为达到最长时间后,寻找不属于ICS(Inevitable Collision States)状态XICS的子节点并返回,即最优节点ni∉XICS。同时使用分析扩展(Analytic Expansions)进行抽样扩展,生成节点与终点直连的路径和速度曲线,无碰撞后的路径及其速度曲线将直接用于最终路径,搜索过程及结果如图5所示。使用分析扩展的方式,解决了离散空间内搜索算法不能够准确到达目标状态的问题。除此之外,通过离散控制量的方式在连续空间搜索得到的结果并不是全局最优的和完备的,且随着离散精度的降低,到达目标状态的精度、最优性和完备性逐渐下降,文献[1]通过实验证明,选择合理的离散精度能够获得接近全局最优和完备的结果。

图4 算法流程图Fig.4 Flowchart of algorithm

图5 时空搜索结果Fig.5 Spatiotemporal search result
节点的索引值由(x,y,θ,t)组成,同一栅格内的节点具备相同的索引值,但不会将节点坐标值映射到栅格中心。生成有效子节点的方式为遍历离散的控制量,获取不处于关闭列表、静态障碍物碰撞检测和动态障碍物时空检测均为安全的节点。得到有效子节点集合后,对其进行遍历,把不处于开启列表的子节点插入到队列,并将子节点与历史节点进行对比,选择较优节点替换队列中的原有节点。
2.2 碰撞检测
按照速度将环境E中的障碍物O分为静态障碍物OS和动态障碍物OD。假设在上层系统中已对动态障碍物OD进行跟踪预测,任意动态障碍物OD,i,i∈{0,1,…,N},N为动态障碍物总数量,均可使用其凸包络拟合的矩形框表示,包含一条或多条行驶预测轨迹Pi。每条预测轨迹由一系列按照时间排序的点组成,每个点有位置、时间、速度和加速度信息,本文暂未考虑预测轨迹的置信度。
OS形状迥异,凹凸形状不定,无论是转化为圆形还是多边形,都存在转化误差和较大计算量。车辆并非标准的圆形,采用图6所示的多个圆近似表示,将车辆转化为多个拟合圆圆心连接成的线段L。本文使用栅格法表示OS,对所有OS进行膨胀。使用L在经过膨胀后的位形空间内进行安全检测,以此在搜索过程中完成高效的静态障碍物碰撞检测。

图6 碰撞检测方法Fig.6 Collision detection method
OD具备较规则的形状,为达到快速准确碰撞检测的目的,本文将所有动态障碍物转化为单一或多个圆形。使用时间间隔(Time Interval, TI)的概念,将OD,i的预测轨迹Pi按照等时间间隔离散化为M段,如图7(a)所示。图7(b)中动态障碍a、b、c分别按照加速、减速、匀速运动,其预测轨迹在相同时间间隔内的长度不尽相同。本文对每一段时间间隔内的轨迹进行线性化处理,按照当前扩展子节点εk的时间,选择对应时间间隔内所有轨迹段进行快速交叉性检测:将εk∩Pi,ti-ti+1=∅(i=1,…,N)确定为安全状态,即图3中运动基元εk与该时间间隔Ii内的所有预测轨迹线段均无交集。

图7 预测轨迹时间间隔Fig.7 Time interval of prediction trajectory
2.3 启发式函数
增加时间维度将大幅降低搜索算法的时效性,本文提出一种联合启发式算法以提高搜索效率。在保留距离启发式函数hd的基础上,增加包含时间维度的速度启发式函数ht,ωd、ωt为距离启发式和速度启发式的权重系数,以h=ωdhd+ωtht加权组合距离启发式和速度启发式,在平面域和时间域内指引搜索树快速到达目标状态。
选择Dubins曲线长度作为距离启发式函数,并根据上文“舒适性模型”确定转弯半径。Dubins 曲线由最小转弯半径形成的弧线线段和直线线段组成,满足可接受性;节点扩展时使用相同转弯半径,满足一致性。本文采用梯形速度规划法计算到达目标状态的时间,以此作为速度启发式函数。根据距离启发式的长度sh,在最大速度vmax的约束下,使用梯形速度规划法计算当前状态(s0,v0)到目标状态(sg,vg)的时间,以到达目标状态的时间作为启发式数值,不能到达目标状态则时间为无穷大。图8为两种典型场景中的梯形速度规划结果。

图8 梯形速度规划结果Fig.8 Results of trapezoidal velocity planning
按照梯形特征将行驶长度分为3段,各段长度分别为s1、s2、s3,sh=s1+s2+s3。得到图8(a)所示场景的计算方法为

图8(b)所示场景的计算方法为

根据式(6)和式(7)计算得到s1、s2、s3,进而得到总耗时。使用距离和速度共同作为本文方法的启发式函数,可达到降低搜索节点数量和加快搜索速度的目的,是在时空栅格内快速搜索的重要前提。
3 实验与分析
3.1 定性分析
为验证本文时空搜索方法在非结构化动静态混合环境中的有效性,本文在仿真环境中设置大量典型场景,并与在静态和动态环境中常用的混合A*算法(Hybrid State A*)和速度障碍法(Velocity Obstacles,VO)进行比较。基于路径速度解耦规划的思想设计一种HAWG(Hybrid State A*&Wait and Go)方法:该方法采用混合A*算法搜索得到与静态障碍物无碰撞的路径,基于路径不变、改变速度的方式规避动态障碍物,实施时考虑按照预设速度行驶会发生碰撞的第一个动态障碍物,通过减速甚至停止等待的方法避让该动态障碍物。分别使用本文方法、HAWG方法和VO方法在多个场景中进行实验,感知范围为20 m,运动过程中按照10 Hz 进行运动规划,在仿真行驶中暂未考虑控制误差和感知的不确定性。图9 中运动规划的起点为100 ms后智能车预期所在位置Ls,并非其当前位置Le,以此达到连续行驶时轨迹间的时间连续性。但在接近目标点时将不断校验轨迹是否可行,可行的轨迹将直接返回。

图9 重规划起点选择方式Fig.9 Start point selected method of replanning
图10 所示仿真环境中,下侧方框为运动规划起点,上侧方框为终点,起点和终点的车速均为0,箭头方向为动态障碍物的运动方向,动态障碍物的运动暂未考虑相互干涉和碰撞。本文方法在实验中设置的关键参数如下:位置精度为0.2 m,朝向精度为5°,加速度为1 m·s-1,时间间隔为0.2 s。本文方法和HAWG 方法的仿真平台长宽分别设置为4.24 m和1.84 m,碰撞检测时拟合为3个圆,各方法均设定最高车速为6 m·s-1。为便于在各场景内使用VO 方法,将所有静态和动态障碍物设置为圆,本文方法和HAWG方法按照前文方法将圆投影和膨胀后进行碰撞检测。3种典型仿真场景中障碍物类型分别设置为仅静态障碍物(场景1)、仅动态障碍物(场景2)和动静态混合(场景3)。静态场景为模拟S形障碍;动态场景是从数据集ETH中抽取得到的行人运动场景[10],并将行人运动数据映射到仿真地图中;动静态混合场景中包含多个相向和同向行驶的动态障碍物和静态障碍物,构建时在场景2的基础上增加了静态障碍物。3种场景中起点与终点距离分别为35.9,30.5,30.5 m,设定单次实验成功的条件为不发生任何形式的碰撞,且在60 s内到达目标位置和速度。

图10 实验场景及行驶轨迹Fig.10 Experimental scenes and drive paths
3 种方法得到的全局行驶轨迹如图10 中曲线所示。VO 方法在场景1(静态障碍物数量为72)中无法规划出到达终点的轨迹,在场景2(动态障碍物数量为9)和场景3(静态障碍物数量为23,动态障碍物数量为9)中的行驶轨迹均较长;本文方法和HAWG 方法能够在所有场景中规划出直达终点的有效轨迹。图11 为行驶过程中某一帧规划结果,HAWG方法不具备主动避让动态障碍物的能力,属于被动避让,在图11(a)所示的相向行驶场景中出现碰撞,在图11(b)所示的相同场景中,本文方法规划出主动躲避动静态障碍物的轨迹。结果表明,本文所提的在时空栅格中进行搜索的方法,在仅静态环境、仅动态环境和动静态混合场景中均能够快速实现主动躲避静态和动态障碍物,具备较强的环境适应性,能够安全引导智能车到达终点。

图11 单帧规划结果Fig.11 Single frame planning results
根据图12(a)行驶总耗时的统计结果可知:HAWG 方法在静态场景中的行驶耗时比本文方法短1.4 s,这是由于本文方法在生成运动基元的过程中,考虑了车辆速度和转弯半径的相互限制;在存在动态障碍物的场景2 和场景3 中,HAWG 方法行驶时间远高于本文方法,且在图11(a)所示的两类场景中均发生碰撞,认定为行驶失败。VO 方法在有可行解时(场景2 和场景3)行驶时间与本文方法相似,但在包含大量静态障碍物的环境中处于无解状态(场景1)。图12(b)为本文方法在图11(b)场景3的行驶速度曲线,该曲线在第8 s 规划出“停止-等待”的纵向速度信息,表明本文横纵向耦合避让的方式能够自动得到“停止-等待”的纵向决策,无需单独进行离散型决策。以上场景内的仿真实验结果验证了本文方法在动静态混合场景中的有效性。

图12 实验结果Fig.12 Experimental results
3.2 定量分析
为进一步验证环境的密集程度和感知范围对各方法的影响,本文在不同静态障碍物数量、动态障碍物数量和感知范围下,统计各方法的成功率和行驶总耗时。VO方法因不考虑加速和转向等运动学约束,故不考虑其行驶总耗时。默认实验环境参数为:10 个静态障碍物,10 个动态障碍物,感知范围为20 m,运动规划起点和终点分别位于相距50 m 的左右边界处。静态障碍物和动态障碍物的位置和运动方向在50 m×50 m 范围内随机生成,障碍物半径在1~2 m,速度在1~2 m·s-1之间随机产生。其中两组实验场景如图13 所示,分别为设置感知范围为40 m、静态障碍物数量为40 个时随机产生的场景。在每组实验中仅有一个参数被改变,每组参数下各进行50 次实验,各组参数下的实验结果如图14所示。
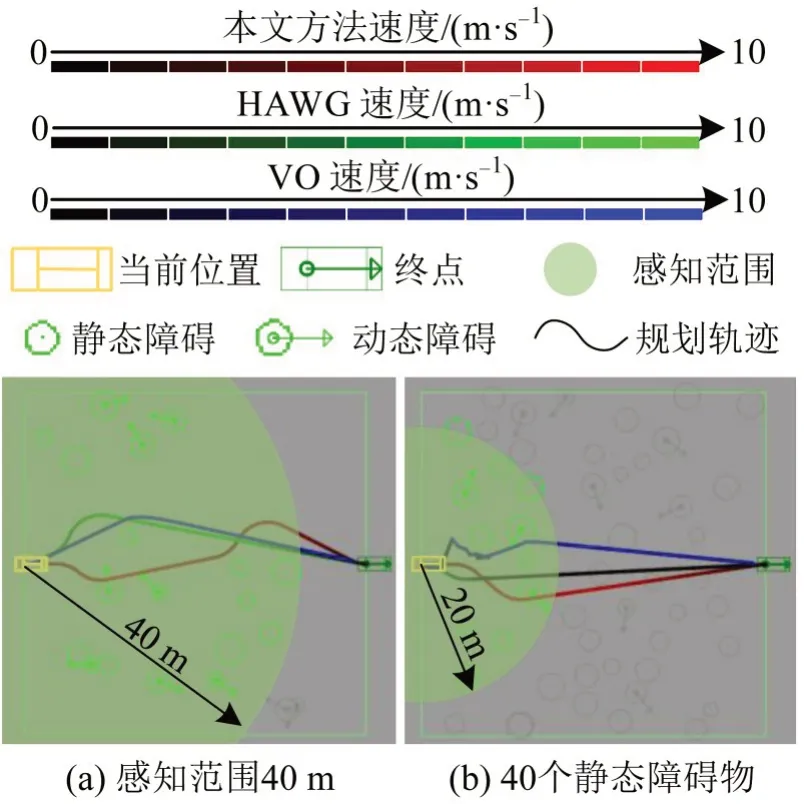
图13 随机场景Fig.13 Random scenes

图14 实验结果Fig.14 Experimental results
从图14(a)可以看出:静态障碍物数量增加对VO方法的行驶成功率影响最大,在40个静态障碍物时成功率下降至38%;HAWG方法由于不能够主动避让动态障碍物,随着静态障碍物的增加,其行驶耗时的标准偏差较大,稳定性较本文方法差;本文方法的行驶成功率受静态障碍物稀疏程度影响较小,行驶耗时比HAWG 方法略短。随着动态障碍物数量的增加,如图14(b)所示,本文方法、HAWG 方法和VO 方法成功率分别降低至42%、30%和45%,说明各方法对存在密集动态障碍物环境的适应能力均有所欠缺,其中HAWG 方法行驶成功率下降最为明显,行驶耗时增长最快;在动态障碍物数量增加到40 时,VO 方法成功率成为最高,说明该方法对密集动态场景具备一定的适应性;本文方法在障碍物数量达到40 之前的成功率均高于其他方法,行驶耗时增幅远小于HAWG 方法。如图14(c)所示:在默认环境中随着感知范围的增加,本文方法具备最高的成功率;各方法成功率和行驶耗时受影响不大,这是由于各方法都具备较高的实时性,在较为稀疏的环境中,不易陷入“死胡同”等局部最优场景。
图14 和表1 所示的平均成功率表明:VO 方法在密集静态场景内(40 个静态障碍物)适应能力较差,成功率仅有38%,平均成功率为各方法最低(58.5%);HAWG方法在密集动态场景(40个动态障碍物)内的成功率仅有30%;本文方法在各类环境中行驶成功率均高于其他方法,在所有环境中的平均成功率为82.8%,比HAWG 方法和VO 方法分别高出19%和23.4%,在稀疏的默认环境内平均成功率达到最高的91%。

表1 平均成功率Table 1 Average success rate(%)
图14和表2所示的行驶耗时表明,本文方法与HAWG方法相比,在不同动态障碍物数量的实验中平均耗时减少30%,在动态障碍物数量增加到40时,行驶耗时减少41%,在所有场景内的平均行驶耗时缩短21%,表明本文方法在考虑车辆运动学约束下的行驶效率高于HAWG方法。
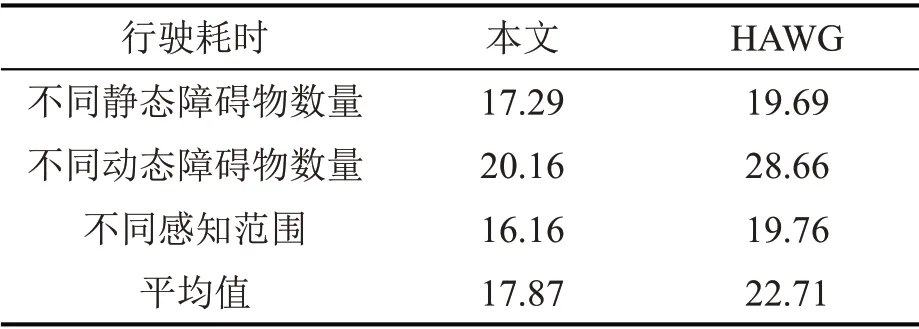
表2 平均行驶耗时Table 2 Average time cost(s)
4 结论
本文所提基于时空栅格的运动规划方法能够融合离散的横纵向决策信息,简化智能车决策层的数量,提高智能车在非结构化动态环境中的适应性;面对不同稀疏程度的环境和不同的感知范围都具备一定的适应性,平均成功率达到82.8%;500次随机场景中的实验结果表明,在行驶总耗时和平均成功率方面均有所提升。
