网联车辆编队的鲁棒模型预测控制方法
2022-08-30张佩瑜周建山田大新
张佩瑜,周建山,田大新*
(北京航空航天大学,a.交通科学与工程学院;b.车路协同与安全控制北京市重点实验室,北京 102206)
0 引言
近几十年来,交通需求的快速增长对道路通行能力、交通效率和交通安全提出了更高的要求。一些先进的车联网技术,如车间通信技术(Vehicle to Vehicle,V2V)已经应用于车辆编队控制以提高道路通行能力[1]。网联车辆编队控制通过车间通信技术,保证车车间实时共享状态信息,使得车辆能够根据相邻车辆的运动状态及时改变自身运动状态,从而使整个车队形成稳定编队[2]。
目前,国内外科研人员针对智能网联车的编队控制问题进行了大量研究,Gong等[3]提出基于约束优化和分布式计算的编队车辆跟踪控制方案,以保证整个车队形成稳定编队系统并减少交通流震荡情况。LAN等[4]考虑了一种分布式最小-最大模型预测编队控制策略,并证明了系统的稳定性,该控制策略能够在存在车间通信延迟和现实约束的情况下满足车队系统的稳定性。MALIKOPOULOS等[5]研究了自动驾驶车队的最优速度控制问题,并用Hamiltonian 理论推导出最优速度控制模型的解析解。此外,仿真实验表明,提出的控制方案可以减少车队的燃油消耗和行驶时间。针对高速公路自动化系统,ZHENG等[6]研究了具有单向拓扑的异构车辆编队控制问题,对于每辆车分配一个局部开环最优控制模型,并设计基于等式的终端约束以确保系统的稳定性;此外,进行了大量的仿真实验,实验结果表明,所提出的最优控制模型和算法能够保证车辆完成编队任务。
目前,有关车辆编队控制的研究有一定的局限性,当设计的控制优化模型与实际的被控车辆存在一定差异度时,控制器往往得不到可靠的控制效果。例如当车辆处于能见度低的环境下,传感器可能受到外界环境干扰致使测量信息不准确[7]。此时,设计的控制模型与实际被控车辆发生模型失配问题。因此,对于含有不确定性因素的鲁棒控制系统研究称为控制领域的热点[8]。GAO等[9]分析了车辆稳定性边界和参数不确定性对编队控制策略的影响,利用干扰观测器来获得汽车稳定状态参考值,并设计了分布式鲁棒模型预测控制器来实现车辆无偏轨迹跟踪;实验表明,提出的协同控制策略能够实现高效编队的同时减少参数不确定性的影响。XU 等[10]考虑了坡度、空气阻力和无线通信延迟等外部干扰对弯道上异构车辆排影响,设计了纵向状态H∞鲁棒控制器,以确保在存在外部干扰的情况下,整个车队实现稳定编队。
基于上述讨论可以发现,目前关于鲁棒控制研究中,传统控制系统的设计通常采用状态反馈策略来控制系统不确定参数,且系统的不确定参数构造单一、固定且状态始终可测。但在实际场景下,系统结构的不稳定状态往往无法准确估计。因此,当编队控制系统结构存在不可测扰动时,传统控制方法达不到期望的控制效果。基于此,本文针对具有结构不确定扰动的网联车辆编队问题,构建编队系统结构不确定的新的表征方式,将不确定干扰约束在某一范围进行优化,在盒式不确定集下建立最小最大范式下的鲁棒预测控制模型[11],为了处理不确定干扰带来的计算难题,基于鲁棒对等理论推导出计算上易于求解的上图优化模型,最后通过仿真实验验证了模型的有效性。
1 传统网联车辆编队控制模型
1.1 问题描述
如图1所示,考虑直道上网联车辆编队控制问题,包括具有已知轨迹的领头车辆和N辆跟随车辆。车队中所有车辆都已安装车载传感器控制器用于感知每辆车的运动状态,然后通过无线通信信道向领头车辆传送信息。车辆i的离散时间动力学方程为
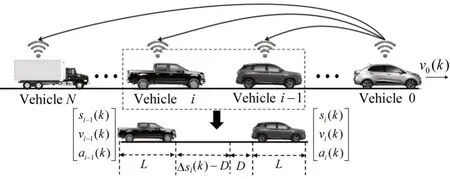
图1 车辆编队控制问题场景Fig.1 Vehicle platoon control problem scenario

式中:τ为参数;k为离散时刻;si(k)、vi(k)和ui(k)分别为车辆i的纵向位置、速度和加速度。
定义车辆i-1 与车辆i速度差为Δvi(k)=vi-1(k)-vi(k),距离差为Δsi(k)=si-1(k)-si(k)-r·vi(k)-L,其中,L为车辆长度,r为恒定反应时间。定义状态量xi(k)=[Δsi(k),Δvi(k)]T,控制输入量为ui(k),车辆i的空间形式为
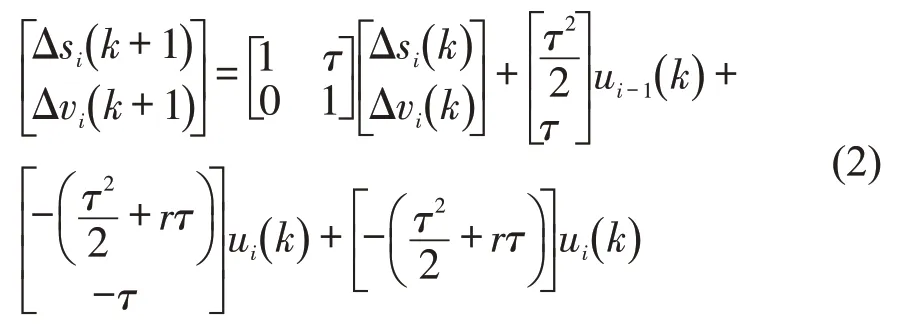
式(2)可以整理为

排中车辆i受到几个重要的状态和控制约束如下。
(1)控制约束。umin≤ui(k)≤umax,其中,umin、umax分别为最小、最大加速度。
(2)速度误差约束。ve,min≤vi-1(k+1)-vi(k+1)≤ve,max,其中,ve,min≤0 为两车之间允许车速误差的最小值,ve,max≥0 为两车之间允许车速误差的最大值。
(3)距离误差约束。de,min≤Δsi(k+1)-D≤de,max,其中,D为两车之间的期望距离,de,min≤0 为两车之间允许距离误差的最小值,de,max≥0 为两车之间允许距离误差的最大值。
1.2 传统网联车队建模
定义编队系统的状态量x(k)=[x1(k)T,x2(k)T,…,xN(k)T]T,控制输入量为u(k)=[u1(k)T,u2(k)T,…,uN(k)T]T,得到线性时不变编队系统模型,其离散形式为
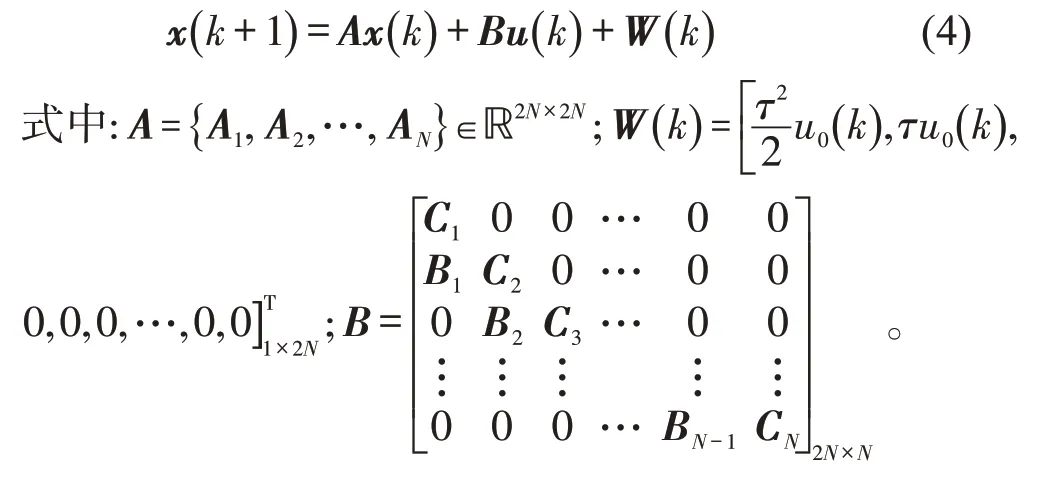
定义

则编队系统的状态约束集和控制约束集为

车辆纵向跟踪控制方案的目标主要包含两方面:一是状态方面,相邻两辆车之间应保持期望的安全间距D,即减少相邻两车间距和速度的变化;二是控制方面,所有车辆的控制信号(加速度)也应该趋近稳定值0 m·s2。基于上述约束和目标,提出无干扰的编队控制模型M1为

模型M1为针对网联车辆编队场景的预测控制模型,当状态矩阵A和B具有不确定扰动时,此控制模型将不能保证车辆形成稳定编队。下面将针对存在结构不确定干扰的编队系统,提出最小最大范式下的预测控制模型。
2 鲁棒模型预测车辆编队控制模型
2.1 最小最大范式下的车辆编队控制模型
在状态空间式(3)中,矩阵A和B是实值矩阵。但在实际场景下由于噪声干扰等因素,A和B具有不确定干扰。具体地说,假设A和B矩阵的形式为

式中:A0和B0为已知的名义矩阵;AΔ和BΔ为扰动矩阵;ζΔ为扰动变量。
为了处理带有扰动变量的状态空间方程,假设不确定变量ζΔ属于盒式不确定集U[11],盒式不确定集U的具体形式为
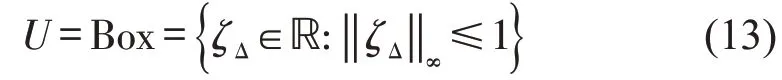
当扰动变量ζΔ∈U时,ζΔ的取值范围为[-1,1],因此状态空间矩阵A和B在盒式不确定集下的取值范围为[A0-AΔ,A0+AΔ] ,[B0-BΔ,B0+BΔ] ,则具有不确定扰动的状态空间方程为
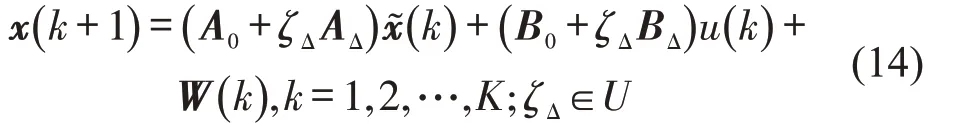
基于式(14)系统的不确定性描述,考虑最小最大化范式下的预测控制模型M2为

2.2 盒式不确定集下的上图优化模型
在模型M2中,目标函数J(u(0),u(1),…,u(K-1))中存在系统结构干扰矩阵,为了处理目标中系统不确定状态矩阵,根据上图优化理论将优化目标转为约束[12],模型M2转化为上图优化模型M3,即

下面,通过鲁棒对等理论处理模型M3 中的不确定约束。
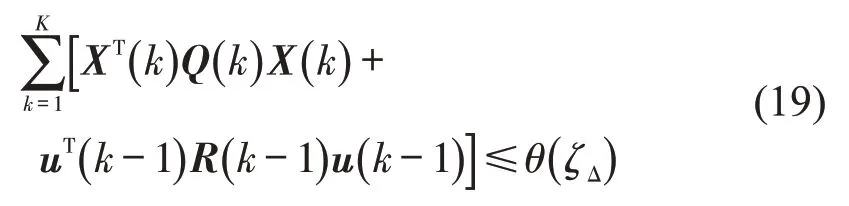
式中:X(k+1)=(A0+AΔ)X(k)+(B0+BΔ)u(k)+W(k),且X(k+1)≥x(k+1)。
证明:状态约束中ζΔ属于盒式不确定集ζΔ∈[-1,1],因此可得到状态x(k+1)的上界为
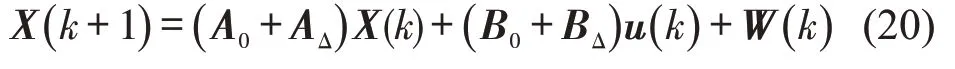
定理2 约束集X(k)∈χ,k=1,2,…,K的等价形式为
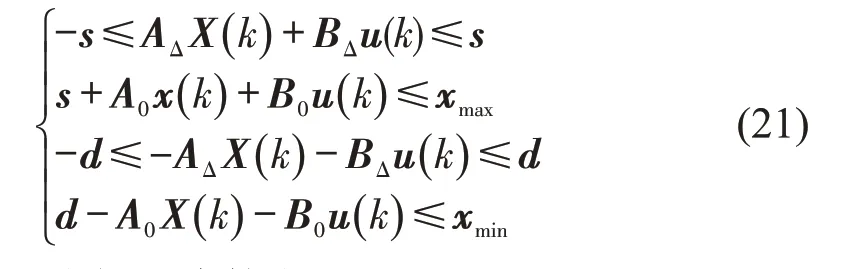
式中:s,d为辅助决策向量。
证明:基于具有不确定扰动状态空间方程式(14),将X≤xmax展开为

式中:∀ζΔ:‖ζΔ‖∞≤1,基于在最差情形原则,可以得到

根据鲁棒对等理论,可以推导出X≤xmax的鲁棒对等模型为

通过定理1和定理2,在盒式不确定集下,得到模型M3在数学上易于求解的上图优化模型M4为

基于鲁棒对等理论,得到模型M2 在盒式不确定集下的上图优化模型M4。对于非凸非线性模型M4,采用序列二次规划算法进行求解。首先,基于泰勒展开式将原始非凸模型转化为一系列凸二次规划子问题,然后选取罚函数为度量函数,根据线搜索方法确定步长,最后对海塞矩阵的正定逼近阵进行修正,直至找到最优解。
3 算例分析
3.1 仿真环境与实验参数设计
本文基于MATLAB/Simulink 搭建车辆编队系统仿真环境并开展仿真实验验证。编队场景由领头车辆和5辆跟随车辆组成。其中,领头车辆作为参考车辆,为其他后方编队车辆提供参考轨迹信息,其他5辆汽车根据头车的参考轨迹信息执行控制以实现稳定编队目标。基于Gong 等[3]提出的仿真实验场景,提出如下参数设计。
领头车辆的初始位置和速度为(s0(0),v0(0),u0(0))=(175 m,25 m·s-1,0 m·s-2), 在t∈[21,24] s 内减速,减速度为-2 m·s-2,并保持一个恒定的速度,直到t=57s开始加速。在t∈[57,60] s 内加速,加速度为2 m·s-2,间段加速度为0 m·s-2。整个仿真的时间设置为100 s。跟随5辆车的初始位置、速度和加速度分别为


对于系统中的名义矩阵A0和B0与扰动矩阵AΔ和BΔ,取名义矩阵,对于扰动矩阵AΔ和BΔ,考虑编队车辆的状态具有干扰,并将扰动矩阵AΔ设置为名义矩阵A0的0.1%。因此。模型中其他参数设置如表1所示。

表1 参数设置Table 1 Parameter setting
3.2 优化结果
仿真实验结果如图2~图5 所示,图2 为领头车辆的加速度,图3~图5 分别为编队车辆的加速度、速度与位置。在模型M4 的控制方案下,5 辆跟随车辆以25 m·s-1的期望速度跟随领头车辆,且整个车队的运行轨迹比较平缓且无碰撞。

图2 领头车辆加速度Fig.2 Acceleration of leading vehicle
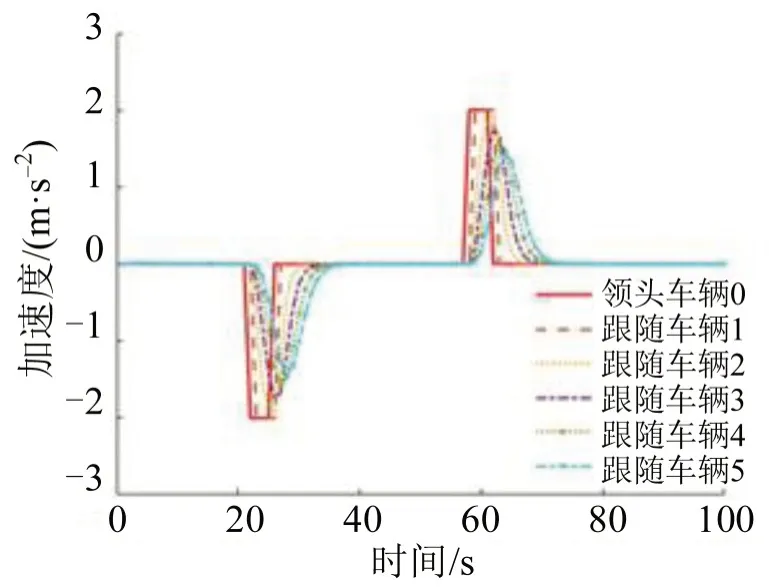
图3 编队车辆加速度Fig.3 Acceleration of vehicles in platoon

图4 编队车辆速度Fig.4 Speed of vehicles in platoon

图5 编队车辆位置Fig.5 Position of vehicles in platoon
此外,设计对比实验验证基于鲁棒编队控制方法的有效性。首先,通过求解传统网联车辆编队模型M1,得到无系统结构不确定扰动的传统编队控制策略,通过求解模型M4,得到鲁棒编队控制策略。将两种控制策略分别应用于具有不同结构不确定扰动的状态方程式(14),在实验过程中考虑系统状态的扰动矩阵AΔ,取其扰动值为名义矩阵A0的0.1%与1%[11],在两种扰动情况下,可分别得到两种控制策略下相邻车辆轨迹差与速度差。

图6 鲁棒控制策略下的车间位移差Fig.6 Vehicle spacing under robust control strategy

图7 传统控制策略下的车间位移差Fig.7 Vehicle spacing under nominal control strategy

图8 鲁棒控制策略下的车间位移差Fig.8 Vehicle spacing under robust control strategy
对比图8 与图9 可以看出,当系统结构存在随机扰动时(ζ△∈[-1,1]),鲁棒控制方案下所有跟随车辆将以固定间距形成稳定编队且不会发生碰撞。传统控制策略下,跟随车辆会发生碰撞,从而不能保证编队安全。因此,基于鲁棒对等变换的控制策略有良好的性能,能够保证车队可以抵御系统结构不确定性带来的影响,进而所有跟随车辆实现速度和轨迹跟踪。
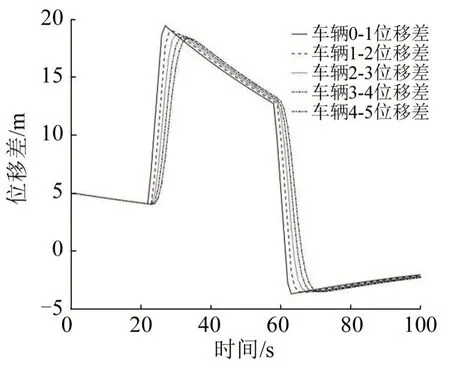
图9 传统控制策略下的车间位移差Fig.9 Vehicle spacing under nominal control strategy
4 结论
本文得到的主要结论如下:
(1)本文提出基于鲁棒对等变换的模型预测编队控制方法,在存在结构不确定干扰时实现对网联车队编队控制。当系统结构扰动矩阵AΔ和BΔ较小时,传统编队控制方法与本文控制方法都能够实现车辆编队目标。这说明该控制方法对干扰大小的敏感度较低。
(2)与传统车辆编队控制方法相比,当系统结构扰动较大时,本文模型的控制效果更优,保证车辆在编队过程中不发生碰撞。后续研究可以考虑在椭球不确定集下的编队控制方法,以提高本文模型对系统不确定扰动的敏感度。
(3)在未来的研究工作中,将在车辆编队预测控制模型中考虑外部扰动,提出针对存在外部扰动的编队控制策略以及算法等方面的内容,从而进一步丰富网联车辆编队控制相关研究。
