基于复杂网络的列车辅助驾驶危险致因传播模型

2022-08-30张仕杰唐涛刘金涛李辰岭

交通运输系统工程与信息 2022年4期

张仕杰，唐涛*，刘金涛，李辰岭

（1.北京交通大学，a.轨道交通控制与安全国家重点实验室，b.国家轨道交通安全评估研究中心，北京 100044；2.华威大学，制造工程学院，考文垂CV4 7AL，英国）

0 引言

随着人工智能技术的发展，计算机视觉、激光雷达探测等多种智能感知技术被引入到列车运行控制领域，开始出现一类基于智能感知的列车辅助驾驶系统（Intelligent Awareness-based Train Driving Assistance System, IATDAS）。这类系统使得列车具备自主检测前方列车、人或其他障碍物的功能，提高了司机的环境感知能力，可以在原列控系统故障降级时显著提高司机的允许驾驶速度。但与此同时，一旦IATDAS 系统存在安全问题，将可能造成列车运行事故。

与既有列车控制系统相比，预期功能安全问题（Safety of the Intended Functionality, SOTIF）[1]是IATDAS系统安全的主要特点。SOTIF问题由智能感知技术的引入而产生，区别于传统由随机失效和系统性失效引发的功能安全问题，该问题与失效无关，而是源自于系统本身性能局限性所产生的预期外系统行为，以及人员对于系统的合理可预见的误用。为了给IATDAS系统建立有效危险防控，分析其SOTIF 类型危险致因的传播机制是不可忽视的一环。

SOTIF 相关危险致因可以通过以系统理论过程分析（System-Theoretic Process Analysis,STPA）为代表的系统性危险分析方法进行辨识[2]。基于STPA 辨识出的危险致因来自于控制结构中的控制、执行、反馈等各个环节。由于这些环节相互作用、相互影响，危险致因之间形成了网状化的因果作用关系，即构成一种危险致因网络。复杂网络（Complex Network）作为研究网络中复杂动态传播过程的理论工具，已被广泛用于危险致因传播的分析。胡立伟等[3]将交通拥塞风险因子的传播抽象为复杂网络中风险因子的传染过程，并以此进行分析给出免疫控制措施。王岩韬等[4]提出适用于航班运行的易感、感染和恢复（Susceptible, Infected, and Recovered,SIR）复杂网络模型，对航班运行风险传播机理进行分析。在铁路领域，Ma等[5]建立了无向的高铁事故致因传播网络，并分析了该网络的拓扑特征。Luo 等[6]利用容量-负载模型仿真铁路事故致因网络中的致因非线性传播，对致因传播的影响程度进行定量分析。考虑到致因传播的有向性，种鹏云等[7]建模分析了危险品运输关联网络的级联失效机理及耦合特性。Liu 等[8]建立有向的铁路事故致因网络，利用容量-负载传播过程定量分析致因传播的影响范围。综上可见，复杂网络理论可用于分析SOTIF相关危险致因的动态传播机制。

但是，现有基于网络的致因传播分析方法大多基于同构网络，即网络中的节点皆属于同一类型，而基于STPA辨识出的SOTIF危险致因包括两种类型，即不安全控制行为（Unsafe Control Action,UCA）及其致因因素（Causal Factor, CF），因其构成的危险致因网络属于异构网络，现有传播分析方法难以准确分析。另外，基于STPA 的分析从系统整体角度进行SOTIF相关致因辨识，使致因具有全局性因果关联关系，而现有研究中的容量-负载模型都采用基于局部网络结构的危险程度分配规则，难以准确反映这种全局性因果关系特征。

因此，本文设计面向IATDAS 系统SOTIF 安全问题的异构致因网络构建方法，提出基于全局容量-负载传播机制的致因传播模型，并以一种典型的IATDAS 系统——列车智能障碍物检测系统（Train Intelligent Detection System, TIDS）为例，应用该模型对其SOTIF 相关危险致因的传播进行分析。

1 IATDAS系统SOTIF相关危险致因网络构建方法

IATDAS 通过多种传感器及人工智能算法进行环境感知，向司机提供当前位置、前方障碍物、限速等信息，系统的功能结构如图1所示。

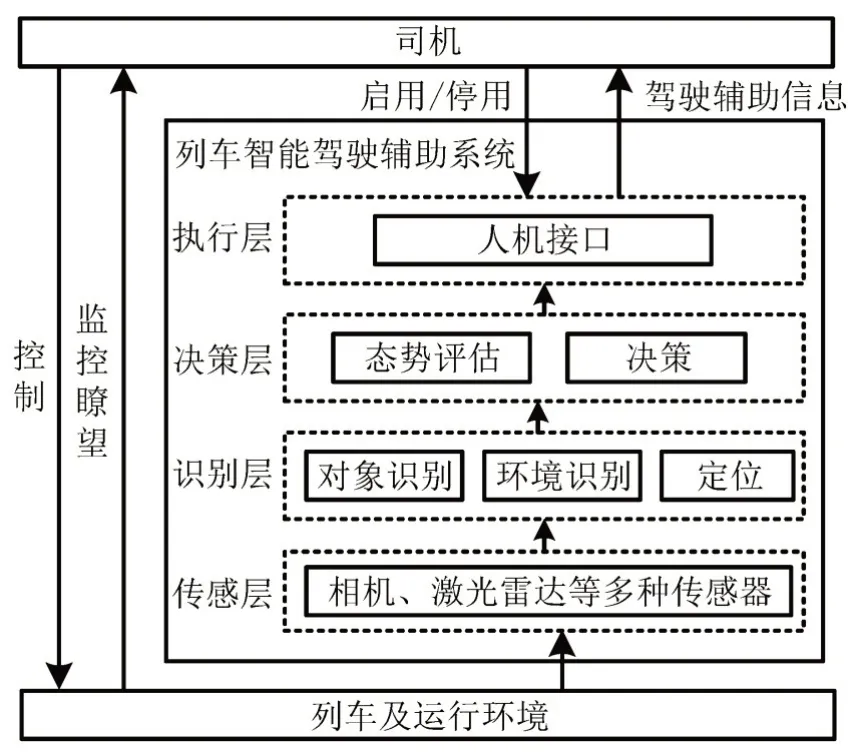
图1 IATDAS系统的功能结构Fig.1 Functional structure of IATDAS

针对IATDAS系统SOTIF 相关致因的辨识，文献[9]给出了基于拓展STPA 的方法。通过该方法可以得到UCA及CF两种类型的危险致因，限于篇幅，此处不再赘述。

SOTIF相关的危险、危险致因及其因果关系路径构成若干包含不同类型节点的致因链。致因链以某个危险为终点。其中，危险由UCA直接导致，而UCA由CF或由多个CF构成的因果链引发。由于同一个危险或危险致因可能存在于不同的致因链中，因此将不同致因链中相同的危险或危险致因合并，即可得到以危险及其致因为节点、以因果关系为边的有向无权的网络。以危险“系统未能防护列车安全的速度/距离限制”（H1）为例，展示异构危险致因网络的创建过程，如图2所示。

图2 危险致因网络构建示意Fig.2 Illustration of network construction

图2 中（a）、（b）两条致因链中，H1 都由“该类目标在传感器无法探测的位置（CF3）”“系统未及时发现人/障碍物（CF4）”“司机未在列车超过与人或障碍物有关的速度/距离限制时提供制动（UCA1）”的因果链引发。将图2 中（a）、（b）相同的点合并，可以得到致因链（d）。同理，将（c）与（d）中同时包含的H1、CF3、CF5进行合并，可以最终得到异构的危险致因网络（e）。

2 基于容量-负载的危险致因传播模型

2.1 模型

利用上述危险致因网络，构建基于容量-负载的危险致因传播模型。该模型由以下3 类要素组成。

（1）容量

本文使用节点容量来衡量施加于危险致因的既有防护水平。其中，既有防护包括系统态势感知的性能、安全屏障，以及人的安全操作和应急干预等多种形式。根据SOTIF相关标准，SOTIF问题应该以致因场景作为安全防护的重点。考虑到致因的可达节点数反映了该致因的潜在致因场景数，即致因可达节点越多代表着该致因能够造成的潜在致因场景也就越多，因此，应对可达节点数多的致因采取更高水平的防护。故模型中将节点容量定义为致因可达节点数的函数为

式中：Ci为危险致因节点的容量；α为用于控制防护力度的可调参数，α ＞0；Ri为危险致因节点i的可达节点数。危险节点作为网络中危险致因传播路径的终点，没有后续可达节点，根据式（1），其容量定义为0。

（2）初始负载

节点的负载代表着相应危险致因或危险事件的危险程度。随着系统的实际运行或危险致因之间的相继引发，节点的负载会发生变化。当节点的负载达到或超过其容量时，节点发生过载，意味着该节点所代表的危险致因或危险的发生。节点i在t时刻的负载用Li（t）表示。

在系统正常工作状态下，各危险致因节点也存在一定的潜在危险程度，即节点的初始负载。节点的可达节点数多，代表致因可导致的潜在致因场景多，同时该致因对系统的潜在危害也大。潜在致因场景多意味着需要更有力的防护，则节点容量大，对系统潜在危害大，则节点初始负载大。参照容量-负载模型在安全领域的应用[5-8]，从简单且不失一般性的角度，设定节点的初始负载与其容量成正比，即

式中：Li（0）为节点的初始负载；β为负载的可调参数，表示初始负载的强度，0＜β ＜1，实际运行中，β反映系统的风险管理水平。

（3）负载分配规则

当危险致因节点发生过载时，该节点的负载会全部流入与其直接相连的后续节点中。负载在危险致因节点之间的重新分配规则定义为

式中：Li为重新分配前节点i的负载；j为一个与i直接相连的后续节点；ΔLij为从节点i向节点j转移的负载量；eij为边ij的因果关系强度；Γi为与i直接相连的所有后续节点的集合；m为任意一个与i直接相连的后续节点。负载Li以边的因果关系强度eij为权重向各个直接相连的后续节点重新分配。在网络全局视角下，一条边ij的因果关系强度eij与该边在网络中参与的节点到节点的路径数量正相关，即通过该条边的因果路径数量越多，意味着该边越容易形成，也即该边的因果关系强度越大。可以用前节点i的直接和间接致因节点数Si与后节点j的可达节点数Rj的乘积（即路径数量）来衡量边的因果关系强度。当没有节点能导致i时，Si为0，则eij单取该边后节点j的可达节点数Rj。

另外，在本文网络中，影响危险节点的只有UCA 节点，而UCA 节点也只会影响危险节点。考虑到危险节点在致因路径的终点，故当计算由UCA 节点向危险节点的负载分配时，不能适用式（3）。在系统运行中，UCA 发生后导致的危险与具体场景有关，因此，本文考虑到一般情况，当负载流入的节点是危险节点时，分配规则定义为负载在多个危险节点之间平均分配。

2.2 可调参数分析

当过载节点的当前负载达到一定程度时，其流出的负载可能继续导致后续节点的过载，即级联过载。容量-负载模型中可调参数的设置应当能够反映系统风险管理水平，使得级联过载过程的发生与实际系统运行情况相符。

在系统实际运行过程中，运行环境的不确定性和人员操作的偏差可能会导致某个危险致因节点的防护能力缺失。如果在模型可调参数设置不合理，仅初始负载就会导致网络中的级联过载，这不符合铁路信号系统风险管理的ALARP（As Low As Reasonably Practicable）原则。因此，为保证在节点的防护能力缺失时，初始负载不会导致网络的级联过载，容量-负载模型应该满足

由式（4）可以得到

式中：为直接导致j的节点数（即该点的入度）。设βc为在节点防护能力缺失时初始负载不会导致网络级联过载的阈值。根据式（6），当可调参数α在不同取值范围时，βc的取值为

式中：、分别为网络中的最大出度、最大入度。根据式（7），当α取1时，βc的值最大。当βc最大时，网络可以承受更大的节点初始负载，即系统在正常运行中可以承受更大的危险程度，此时系统的鲁棒性最强。α的取值反映了系统的防护力度，α取值越大，系统的防护力度越大，需要的人力物力投入也越多。当α=1 时，防护投入不是最大但使系统达到了最大的鲁棒性，符合ALARP 的原则。因此，模型可调参数α的最优值为1。另外，根据式（7）结合具体网络的结构特征可确定可调参数β的取值范围。

3 传播模型应用及结果分析

3.1 案例网络构建

列车智能障碍物检测系统（TIDS）是一种典型的IATDAS 系统，本文选取该系统“车载ATP 失效后TIDS辅助司机驾驶列车”的运行场景，应用所提模型进行危险致因传播分析。其中，文献[9]已识别出该运行场景的3 项系统级危险，分别为“系统未能防护列车安全的速度/距离限制（H1）”“系统未能防护列车超过线路允许速度（H2）”“系统在不必要的时候提供紧急制动（H3）”，并对此3项危险进行了SOTIF 致因辨识。辨识所得的危险致因包括8 项UCA 致因和154 项CF 致因，作为本文危险致因传播分析工作的输入数据。受篇幅所限，本文列举出部分代表性的危险致因，如表1所示。

表1 部分危险致因[9]Table 1 Portion of hazard causes[9]

在识别出的危险致因、危险及其因果关系的基础上，采用第1节中的方法构建异构的危险致因网络，如图3所示。该网络中包含165个节点，代表危险和危险致因。其中，H1～H3 为危险节点，其他节点为危险致因节点，包括8个不安全控制行为节点（UCA1～UCA8）和 154个致因因素节点（CF1～CF154）。此外，按照对应节点之间从“因”到“果”的方向，危险致因与危险以及危险致因之间的因果关系构成了图3中302条有向的连边。

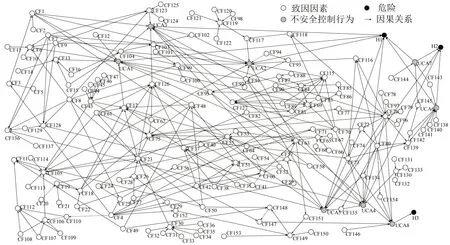
图3 危险致因网络Fig.3 Hazard causes network

3.2 基于案例网络的传播模型对比

当某个节点过载时的负载达到一定程度时，可能会通过级联过载导致一个或多个危险的发生。级联过载过程是否导致危险发生，主要受容量-负载模型中的负载分配规则所影响。合理的负载分配方式可以准确地反映系统中危险致因关系的特点，从而为风险管理提供针对性的支持。

在既有传播模型研究中，常用的节点负载分配规则为平均分配[6]（Average Distribution,AD）或按后续节点的度分配[7]（Distribution by Degree,DD）。而本文模型采用的是基于全局因果关系的分配规则（Overall Distribution, OD）。为了比较这几种分配方式，引入敏感度的概念，即导致危险发生所需的单个危险致因的危险程度，具体定义为节点i导致一个或多个危险发生所需的最小负载与该节点容量Ci的比值。危险致因的敏感度数值越大，代表其越难以导致危险的发生。根据式（7），当α取1时，本网络中负载强度参数β的阈值βc为0.26，因此本文分别选取β值为0.1和0.2进行模型对比，计算全部162 个危险致因节点的敏感度，结果如图4所示。

由图4可见，大多数危险致因（即图中“其他”共计136 个节点）在3 种不同分配方式下敏感度数值均为1，即负载等于其容量就可触发危险。其余26个致因在不同分配方式下敏感度有所不同。其中，有些致因（例如，CF4、CF23、CF26等）在既有传播模型的分配方式下敏感度为1，而在本文所提OD 方式下则大于1，即负载大于其容量才能通过级联过载引发危险；有些致因（例如，CF75、CF38、CF41等）虽然在3 种分配方式下的敏感度均大于1，但在本文OD 方式下则需要更多的负载才能引发危险。综上可见，图4中除“其他”之外的26个致因在本文OD方式下需要更多的负载才能最终导致危险。

图4 不同分配方式下导致危险所需的单节点负载Fig.4 Loads of a single node to cause a hazard under different distribution rules

实际上，上述26 个危险致因具有较长的后续因果传播路径。在系统实际运行中，这些危险致因的传播过程可以通过后续的防护措施得到减轻，从而较难导致危险的发生。例如，对于致因CF4“列车运行在雨、雪、雾霾、沙尘等天气中”，由于设备具有一定的低能见度条件下的态势识别能力，因此一般不会导致危险。只有在一些潜在的特殊情况下，例如列车驶出隧道时随即驶入大雾环境，此时致因CF4的危险程度较高，而设备和司机对环境的变化需要一定的反应时间，可能会因没有识别到前方障碍物而导致危险的发生。因此，从系统运行的实际情况来讲，上述26 个危险致因应该在比较高的危险程度下才会导致危险，这说明对于具有较长后续传播路径的致因，本文所提基于OD分配规则的容量-负载模型更加符合系统运行的实际情况。

3.3 传播模型应用

基于危险致因网络以及容量-负载模型，对TIDS 系统的危险致因传播过程进行研究，分析网络中各节点可能的传播影响范围及传播路径。为确保危险致因通过级联过载在网络中充分传播，本文选取β为0.2，并分别给网络中各个初始节点施加较大的初始负载。通过分析网络中累计过载的节点数量可以确定起始节点的影响范围。设过载节点将负载传递到后续相连节点的时长为1 个单位时间，计算网络中危险致因节点的影响范围随时间的变化情况。由于节点较多，本文针对影响范围变化的不同特征，分别选取各类特征下具有代表性的变化情况，如图5所示。

图5中影响范围较小、在传播初期影响范围增加较慢的致因对危险作用较小，在此不作讨论。针对图5 中其他致因，本文按照以下3 种情况分别制定针对性控制策略。

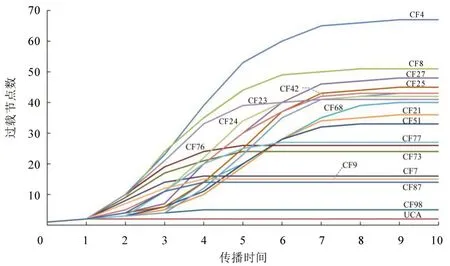
图5 不同节点过载后的影响范围Fig.5 Range of impact after overload of a hazard cause

（1）有些致因在传播初期影响范围增加很快，但很快停止增加，其最终影响范围不大，如CF76（TIDS无列车当前定位）、CF73（TIDS的定位不准确或错误）、CF7（司机忽视了来自TIDS 的提示）。这类节点影响范围小，当危险致因发生后，可以对其所有传播路径采取措施。另外，这类危险致因导致危险发生的速度快，应在其发生后及时进行传播路径控制。

（2）有些致因在传播初期影响范围不大，但后期影响范围迅速扩大并最终引发较多致因，如CF51（该类目标的某些特性造成TIDS 识别困难）、CF21（坡道）、CF68（处理算法未能准确判断距离）。对这些节点的相邻后节点采取措施，即可阻断大部分路径，从而有效阻止此类危险致因影响的蔓延。

（3）有些致因影响范围大且前期影响数增加快，如CF4（列车运行在雨、雪、雾霾、沙尘等天气），CF8（司机在恶劣运行环境下，过度信任来自TIDS的提示），CF27（列车振动），应该成为风险控制的重点。这些致因引发危险的致因路径较多，如CF4、CF8、CF27 到危险的路径数分别为703、402、403。对于这类危险致因的传播过程，在有限成本和资源下应该重点控制传播较快的路径，以降低最终危险发生的速度，为进一步的应急处置赢得时间。具体可通过控制路径上最易过载节点（即敏感度最小）的方式进行重点路径控制。另外，控制这些重要路径上的节点后，包含这些节点的其他路径也可以得到有效控制。

3.4 应用结果讨论

为验证3.3节中针对影响范围大且前期影响数增加快的危险致因所提策略的有效性，本文选取前10%传播较快的路径进行针对性控制，并计算控制后的危险发生速度。作为对照，本文随机控制10%的传播路径并计算危险发生速度，最终以重复该过程30000 次后的平均值作为随机策略下的危险发生速度期望值。两种危险控制策略下的危险传播速度如图6所示。

图6 不同控制策略下的危险发生速度Fig.6 Hazard causes propagating speed under different risk control strategies

由图6 可见，对于一些节点，如CF4、CF8、CF27、CF31～CF48等，随机控制策略几乎不会改变危险发生速度，而采用针对性策略后致因传播速度可以下降30%～100%。对于另一些节点，如CF20、CF54、CF58、CF77，随机控制策略可以使危险致因传播速度平均降幅50%以内，而针对性控制策略可以稳定使危险发生速度降低到0，即危险不会发生。总体上，随机控制策略下只有10%的平均降幅，而采用本文模型的控制策略后，致因的传播速度平均降幅可达到68%。因此，通过采取针对性策略，即控制传播较快的路径，可以在危险致因发生后有效降低危险发生的速度。