给定站点条件下轨道交通线网初步辅助构建模型
2022-08-30刘明敏何鸿杰金安
刘明敏,何鸿杰,金安
(广州市交通规划研究院有限公司,广州 510030)
0 引言
近年各城市陆续开通轨道交通线路,轨网规模逐年扩大[1]。一方面,单位里程轨道建设成本不断增加,资金需求巨大;另一方面,客流效益不足,运营补亏负担较重。由于轨道交通网络建成后难以改变,网络设计和线路选择的在轨道交通线网规划阶段则显得尤为重要。
线网规划理论研究层面:Ralf 等[2]、Bruno 等[3]、Laporte等[4]以系统行程时间为目标进行网络设计,黄超等[5]以社会经济收益为目标进行城市群铁路网络设计,卫振林等[6]以运营效果、线网结构等综合因素为目标对方案进行优选。Dicesare[7]、Current等[8]以总成本最小为目标进行线路选择,Bussieck等[9]、Canca 等[10]以客流覆盖最大为目标确定线路走向。大部分相关研究均在建立数学模型后,使用非精确算法求解最优方案。现有研究成果中,模型复杂导致难以应用于城市大规模站点、多线路计算;网络设计和线路布设时缺乏建设时的工程可行性和开通后的运营约束考虑。
规划实践层面,我国线网规划的技术人员普遍采用“点-线-网”的规划方法,先确定客流集散点,再根据客流走廊和土地利用确定线路走向,最后基于线路确定大致网络形态。在基于给定站点设计网络和布设线路这一问题上,实践主要依据个人技术经验,缺少量化计算,未充分定量考虑建设成本、可行性和服务水平。一方面,规划工作难度巨大;另一方面,初始方案质量难以保证。
综上,本文对城市轨道交通线网规划阶段的轨道交通线网网络设计和线路选择问题进行研究,提出一种定量的线网规划初步辅助构建模型。在模型中考虑线网总里程、直达客流、换乘客流量等目标,并根据实践需求改进求解算法。在给定大规模站点条件下,可以实现网络设计和线路选择等计算,可形成初步方案,便于辅助规划人员进行后续线网规划工作。
1 问题描述
城市轨道交通线网规划实践中,基于给定站点,希望通过最短的轨道网络里程规模,串接选定站点,实现最大客流覆盖范围;同时在换乘次数尽可能少的情况下,构建线路,实现较高的客流服务水平。由于缺乏量化为主的成网技术流程,选定站点较多时,规划人员难以主观确定较优的线网规划方案,故本文根据上述目标建立数学模型并通过算法求解,提出量化初步成网技术流程,为后续线网规划工作提供辅助参考。
上述目标具体为在给定站点和对应站点间的预测客流OD前提下,以网络总里程最小化和直达客流比、一次换乘客流比最大化为目标,建立数学模型,采取逐个节点进行连接,不断变换线路布设方式的策略,求解获得最优网络和线路方案。
(1)决策变量
xij——0-1 变量,站点i和j的邻接关系,若站点i和j之间相互连接且i≠j,xij=1 ,否则,xij=0,xij作为元素组成的对称邻接矩阵为X;
yijk——0-1变量,若在线路k上站点i和j是相邻的两个站点,yijk=1,否则,yijk=0,yijk作为元素组成的对称邻接矩阵为Yk。
(2)其他变量
G——轨道交通网络的无向图;
V——G的站点编号集合;
ε——G的边集合;
K——线路编号集合;
aij——0-1变量,若站点i和j之间相互可达且i≠j,aij=1,否则,aij=0,aij可由邻接矩阵X通过Warshall算法计算得到;
θi,bc——站点i作为顶点,与另外两个不同站点b,c形成的夹角角度;
dij——站点i和j的距离,以时间、长度等形式表示;
tij——站点i至站点j的起讫点客流量;
rd——直达客流比,使用Logit 模型根据tij和Yk计算得到;
rx——一次换乘客流比,使用Logit模型根据tij和Yk计算得到;
ra——rd和rx通过理想点法转化为单目标规划问题的目标值;
ukl——线路k和线路l间复线段的数量;
qik——用于子回路消除约束的辅助变量。
(3)基本假设
为简化问题,提出以下假设:
①忽略换乘的时间成本;
②任意两个相连站点间的距离用直线距离替代实际距离。
2 数学模型
2.1 模型结构
双层模型将从“点-网-线”的角度进行线网规划,首先根据给定站点生成最优网络,然后在生成的最优网络上进行线路布设。模型上层为网络设计模型,以实现站点全部覆盖的网络总长度最小化为目标,基于给定站点生成轨道网络;模型下层为线路选择模型,以直达客流比和一次换乘客流比为目标,基于上层模型生成的轨道网络,进行线路布设。
2.2 网络设计模型
网络设计模型作为双层模型的上层,将基于给定站点初步生成轨道交通网络,其目标和约束为
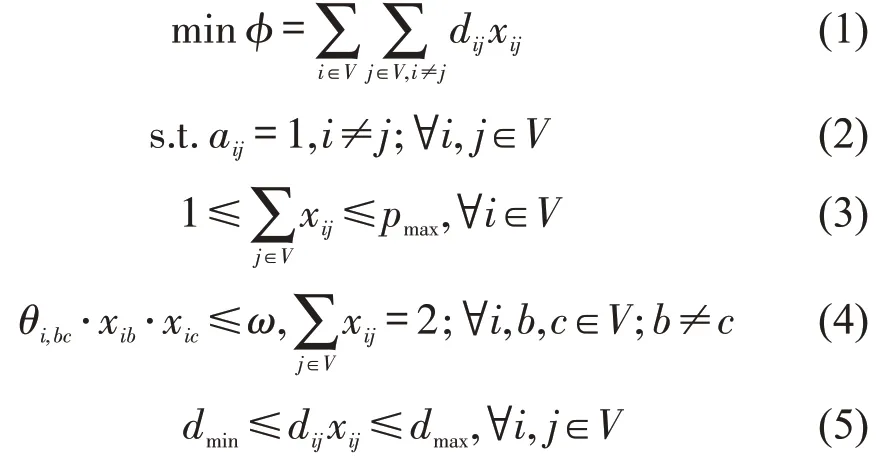
式中:pmax——站点度的最大值;
ω——转向最大角度;
dmin、dmax——任意两个站点间距的最小值、最大值。
优化目标式(1)表示期望实现网络总长度最小化。约束:式(2)表示站点间可达性约束,即生成的网络需要覆盖到全部站点;式(3)表示站点的度约束,即确定与每个站点相连的其他站点的数量范围;式(4)和式(5)均为工程可行性约束,式(4)表示角度约束,网络中站点的度为2的站点所在的欧拉路径,转向角度不能大于ω;式(5)表示站间距约束,限制两个相连站点的间距。
2.3 线路选择模型
线路选择模型的目的是基于上层模型求解得到的网络,进行线路布设,确定线路数量、线路走向和线路经过的站点数量,线路选择模型如下:


式中:r——从rd,rx和ra中选用的目标函数;
τmin、τmax——线路的最小、最大长度;
N1,min、N1,max——线路最小、最大站点数;
N2,max——任意复线段上的最大站点数;
N3,max——任意复线段上的最大线路数;
N4,max——G中出现复线段的最大次数;
M——一个很大的常数。
优化目标式(6)表示最大化目标函数。约束:式(7)表示线路必须在已有网络上布设;式(8)表示连续性约束,确保各个线路连续不能中断;式(9)表示站点访问约束,各个站点至少被线路经过1 次;式(10)和式(11)表示线路长度约束,分别表示线路的长度范围和经过站点数量范围;式(12)~式(14)表示复线约束,分别表示两条线路间复线段包含站点的数量范围、复线段上的线路数量范围和G中出现复线场景的最大次数;式(15)表示角度约束,任意线路的转向角度不能大于ω;式(16)表示Miller 等针对车辆路径规划问题提出的子回路限制约束[11],防止产生环线外的异常环路。
3 网络设计模型求解算法
3.1 基于聚类的最小生成树网络求解
上层模型式(1)~式(5)可转化为带约束的最小生成树求解问题,故使用Kruskal 算法求解上层模型。由于Kruskal 算法的时间复杂度较大,且最小生成树的网络结构与实际城市轨道交通系统的网络结构存在较大区别,为解决以上两个问题,提出基于聚类求解最小生成树方法,操作示例如图1所示,具体步骤如下:

图1 基于聚类的最小生成树求解算法Fig.1 Minimum spanning tree algorithm based on clustering
Step 1 分解。将G中所有站点按照它们的相对位置,使用聚类算法(如Kmeans 算法),将站点分为不同聚类。
Step 2 子最小生成树求解。使用Kruskal算法求解各个聚类中关于站点的最小生成树。
Step 3 合并。将各个聚类的子最小生成树进行合并,组成完整网络,合并的原则是使所有站点间相互可达和网络总长度增加最小。
3.2 生成网络修正
尽管在最小生成树求解过程中加入了式(3)~式(5),但生成的网络与实际轨道交通网络相比,仍会有许多不合理的异常连接方式,这些异常可能会导致线路长度过短、换乘站数量过多、网络非直线系数增加等问题,进而影响线路布设。为消除异常连接方式,提出以下几种生成网络的修正操作,修正操作示例如图2 所示,修正方法如表1 所示。具体修正流程如下:

图2 网络修正方法示意Fig.2 Illustrations of network repair strategies
Step 1 对于通过基于聚类的最小生成树求解算法获得网络,首先检查表1 中所有异常连接方式,并使用表1中对应的修正操作按顺序逐步进行修正。

表1 网络修正方法Table 1 Methods to modify network generated
Step 2 修正操作可能产生新的异常连接,重新检查网络中存在的异常并进行相应的修正操作,若修正操作对应的异常不存在,则跳过该修正操作。
Step 3 重复Step 2 直到网络中不存在异常连接方式为止。
3.3 迭代优选
最小生成树求解算法和聚类算法的计算结果具有不确定性,导致每次生成网络及其总长度大小可能不一致,需要多次进行基于聚类的最小生成树网络求解和生成网络修正,直到最小生成网络里程在多次迭代中不再下降保持稳定,以获得总长度最小的最优网络。
4 线路选择模型求解算法
4.1 网络结构简化
生成网络G中的非换乘站、非起终点站对线路的布设影响较小,通过移除这些站点,获得只包含换乘站和起终点站的简化网络GS=(VS,εS),以简化计算,网络结构简化的示意图如图3所示。

图3 网络结构简化示意Fig.3 Illustrations of simplification of generated network
4.2 求解算法选择和可行解表达
下层线路选择模型式(6)~式(16)属于NP-hard问题,在站点较多时使用精确算法无法求解,因此基于禁忌算法设计求解算法。
每个线网线路方案由可行解表达,单个可行解中包括 |K|条完整线路,每条线路以站点编号序列形式表示,例如{10,2,5,18,…} ,编号的顺序表示线路逐个经过的站点,该可行解形式保证可行解的编码长度可变,使禁忌算法能直接对可行解进行操作,同时降低解空间的规模[12]。
4.3 初始可行解构造
在构造初始可行解时,对式(10)和式(11)进行松弛,忽略线路长度限制。为了使禁忌算法快速找到质量较优的可行解,采用贪心策略构造初始可行解,具体步骤如下:
Step 1 选择GS中任意未被任何线路经过的起终点站或换乘站作为起始点,开始新线路的构造。
Step 2 在GS中,尝试将线路延长至与当前点连接的其他站点,在满足式(7)~式(16)的情况下,将线路延长至客流效益目标值增量最大的站点。
Step 3 若线路延长至起始点外的起终点站或不能继续延长,转到Step 4;否则,重复Step 2。
Step 4 若线路经过至少两个或以上的站点,将该线路加入初始可行解。
Step 5 若没有新线路能够生成,转到Step 6;否则,回到Step 1。
Step 6 为减少不满足式(15)和式(16)最小值限制的过短线路数量,在满足式(7)~式(16)的情况下,合并初始可行解中任意两条线路,直到没有线路能被合并为止。
4.4 当前可行解邻域构造
为禁忌算法构造如下5种邻域操作。
(1)线路交换。
选择当前可行解中的两条相交线路,将它们中的一个换乘站作为中断点,拆解两条线路,然后随机重新组合。
(2)线路拆解
选择当前可行解中的较长线路,线路上的一个换乘站作为中断点,将其拆解为两条较短线路。
(3)直达线路构造
两个起终点站间的最短路站点序列直接作为新线路,新线路可能会与已有线路发生重叠,在发生重叠的位置上,剔除已有线路发生重叠的部分,产生新的较短线路。若剔除部分会将已有线路打断,则进行打断并产生两条新线路代替已有线路;若剔除部分与已有线路完全相同,则移除已有线路。
(4)复线交换
减少GS中一个复线段上的线路数量,即减少复线段上发生重叠的其中一条线路,减少线路数量的过程中,会剔除经过复线段一条线路的重叠部分,剔除方法与(3)相同。同时在GS中的任意其他部分,通过延伸另外一条已有线路的形式,使延伸部分与其他线路发生重叠,增加新的复线段,或在已有复线段上增加重叠的线路数量。
(5)线路合并
合并当前可行解中任意两条线路,直到没有线路能被合并为止。
以上5 种邻域操作生成的新线路必须满足式(7)~式(16),通过5种邻域操作的不同组合可以获得图4所示的6种邻域。

图4 当前可行解的6种邻域Fig.4 Six neighborhoods of current feasible solution
4.5 禁忌表设置和藐视准则
分别为线路交换和拆解操作设置禁忌表,站点i作为中断点,使用某种操作得到的邻域被选为最优解时,对应禁忌表中站点i会被加上禁忌代数θ。在随后θ次迭代中,不能满足藐视规则且再次以站点i作为中断点的对应操作获得的邻域将会被抛弃。禁忌长度与站点数量正相关。
藐视准则是禁忌算法中常用的准则,即对于某个处于禁忌中的邻域,如果该邻域的目标值优于当前最优解的目标值,则该邻域可以直接无视禁忌代数,直接作为当前最优解和当前可行解。
4.6 求解流程
为了降低解决问题的难度,使用禁忌算法分别预先求出rd和rx的最优目标值,再解决两个目标rd和rx同时优化的问题。禁忌算法流程如图5所示。

图5 单目标禁忌算法Fig.5 Tabu Search for single objective problem
在使用单目标禁忌算法求解最优rd和rx后,使用理想点法式(17)将rd和rx同时优化问题转化为单目标规划问题,然后以ra作为目标,再次使用相同算法得到最优方案。传统多目标算法求解的结果为Pareto 解集,需要对Pareto 解集中的方案进行二次评选,过于复杂,而理想点法可直接得到最优方案。相较于传统的线性加权法,理想点法能够保证算法的搜索路径朝向两个目标共同优化的方向。

式中:rd*、r*x——使用单目标禁忌算法得到的最优直达换乘比、一次换乘客流比;
wd、wx——对应目标值的权重。
5 计算实例
5.1 案例介绍
以某市现状城市轨道交通站点为例,使用双层模型自动生成最优线网规划方案。网络结构方面,站点间距离假设为直线距离时,现状网络总里程为475.77 km,共有228 个站点,其中34 个换乘站,现状线路共15 条,网络平均最短路径长度为33.00 km;运营效率方面,日均出行量为518.44 万人次,rd=0.4284 和rx=0.3268。
5.2 网络设计
算法参数设定:pmax=4,ω=90°,dmax=5 km,聚类算法选择Kmeans算法,聚类数量选定为14,迭代求解次数为50次。
根据现状站点,使用上层网络设计模型求解得到的最优网络如图6所示。与现状网络比较,生成网络的总里程减少至467.89 km,换乘站数量仍为34个,平均最短路径长度为33.07 km。自动生成网络与现状网络的网络结构区别不大,主要区别集中在图6 灰色方框处,与现状网络相比,灰色方框处的交叉和冗余减少,平顺性增加。外围区域站点密度较低,成网方式简单明显,这些部分自动生成网络与现状网络相同。
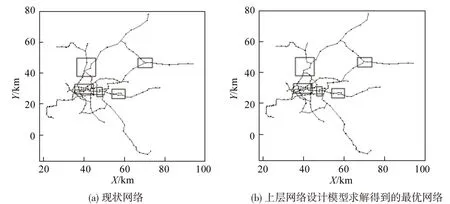
图6 现状网络和上层网络设计模型求解得到的最优网络Fig.6 Existed network and optimal network generated by upper-layer network design model
另外,从图7 可以看到,求解算法在迭代至10次之前已经搜索到最优解,说明算法的收敛速度较快,剩余30次迭代计算最优目标函数值并无变化。
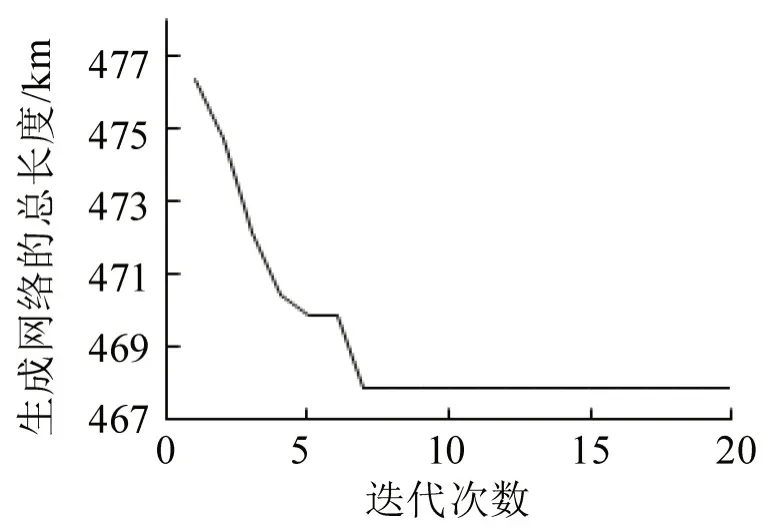
图7 上层模型目标函数值随迭代计算的变化Fig.7 Change in objective function value of upper model with iterative computation
5.3 线路选择
算法参数设定:τmin=0.3 h ,τmax=1.2 h ,N1,min=9,N1,max=32,N2,max=2,N3,max=2,N4,max=1,ω=90°,禁忌算法迭代求解次数为200 次,每次迭代每种邻域构造5个,θ=4,wd=1.5,wx=1.0。
根据生成网络,使用下层模型求解得到的最优线路方案如图8 和图9 所示,不同明暗粗细的线代表不同线路,横纵坐标X和Y表示平面坐标系中的相对位置。运营效率方面,最优方案中包含14条线路,rd=0.4315 和rx=0.3406,均比现状线网高,最优方案具有更好地运营效率。线路走向方面,与现状线路对比,线路数量减少1条,部分线路有一定程度的延长;对于现状换乘量较大的两条线路,算法对其进行了交换以减少换乘次数。
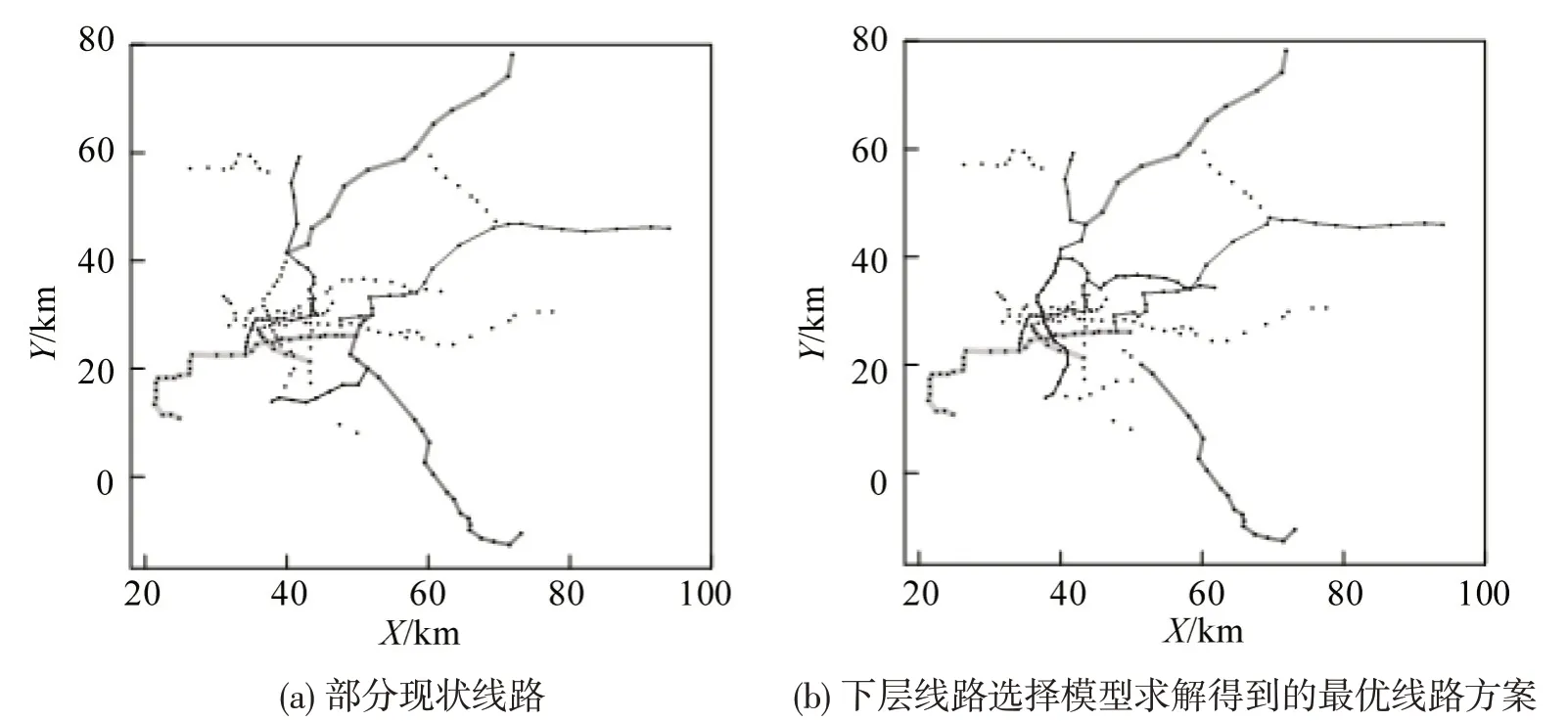
图8 现状线路和下层线路选择模型求解得到的最优线路方案(线路1~7)Fig.8 Current scheme and optimal scheme generated by second-layer line planning model(Line 1~7)

图9 现状线路和下层线路选择模型求解得到的最优线路方案(线路8~14)Fig.9 Current scheme and optimal scheme generated by second-layer line planning model(Line 8~14)
图10 指出,ra、rd和rx分别迭代40,20,60 次左右时目标函数值收敛,说明禁忌算法效率收敛速度较快,能快速获得最优线路方案,剩余100 次迭代并无目标值变化,从图中省略。

图10 下层模型目标函数值随迭代计算的变化Fig.10 Change in objective function value of second-layer model with iterative computation
6 结论
针对城市轨道交通线网规划中网络设计和线路布设问题,本文建立由网络设计模型和线路选择模型组成的双层模型,并设计以基于聚类的最小生成树算法和禁忌算法为核心的求解算法。以实际轨网为例,比较分析实例和模型计算结果。得到结论如下:
(1)网络设计模型可处理大规模站点,快速得到满足站点可达性、工程可行性约束的初步网络。引入的多种网络修复策略,可以自主调整网络结构。模型生成的初步网络相较于实例,形态结构近似,不存在不合理分支,线网总里程更短。
(2)线路选择模型引入贪心策略生成质量较优的初始线路方案,再使用禁忌算法搜寻最优方案,模型生成的初始线路方案的客流走廊与实例近似,且线路交叉和线路总数有所减少,具备更高的直达客流比和一次换乘比。
本文的模型可推广到大城市轨道交通线网规划中,基于选定的客流集散点或候选站点,辅助生成质量较优的初步规划线网备选方案,作为初始方案为后续线网规划工作提供辅助参考。
